基于GIS的西秦岭地区降水量空间插值方法探讨

孙伟红，常直杨

(1.江苏省测绘工程院，江苏 南京 210013； 2.南京旅游职业学院，江苏 南京 211100)

基于GIS的西秦岭地区降水量空间插值方法探讨

孙伟红1，常直杨2

(1.江苏省测绘工程院，江苏 南京 210013； 2.南京旅游职业学院，江苏 南京 211100)

反距离加权法；综合插值法；克里金法；降水量；西秦岭地区

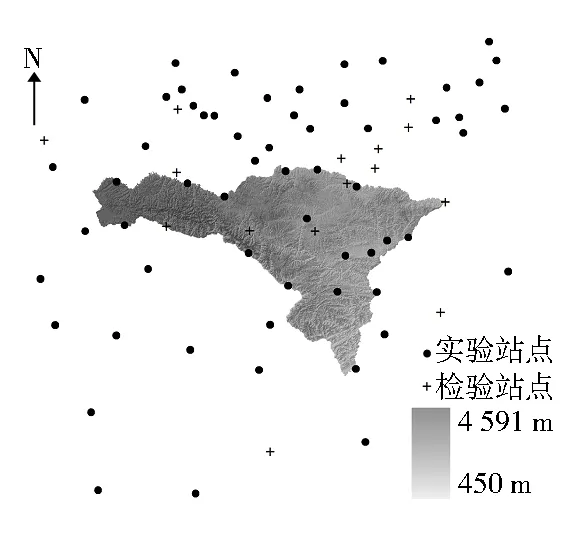
以西秦岭地区周边77个气象站1971—2000年平均降水量为数据源，选取反距离加权法(IDW法)、综合插值法、泛克里金法(UK法)、回归克里金法(RK法)等4种内插方法，探讨了西秦岭地区降水量最佳插值方法的选取。交叉验证结果表明：4种插值方法的精度,IDW法<综合插值法

研究某一地区降水量年际变化特征及其空间分布，对于指导当地农业生产、预报地质灾害等具有重要意义[1-2]，但是在地形复杂的偏远地区，受经济、技术和人力条件限制，气象站点数量有限，获取气象资料难度较大。近些年随着相关技术的发展，通过空间插值生成区域降水要素空间分布图[3-6]成为一种有效的解决办法。在众多的空间插值方法中，最近距离法、反距离加权法等[3]体现了空间几何距离的影响；趋势面法、多元回归法[4]体现了属性数据之间的统计关系；克里金法[5-6]体现了气象要素的原始数据及变异函数的结构特点。每种方法都有其使用范围、算法和优缺点，没有绝对最优的空间内插方法，只有特定条件下的最优方法[7-9]。

西秦岭地区地质构造活跃，滑坡和泥石流等地质灾害多发，研究降水量空间分布对于该地区水土流失治理和地质灾害防治尤为重要。本研究选用4种空间插值方法——反距离加权法(IDW法)、综合插值法、泛克里金法(UK法)、回归克里金法(RK法)，通过对比分析，选出适合该地区的最佳的空间插值方法，以更好地描述西秦岭地区的降水量空间分布。

1 材料和方法

1.1 研究区概况

西秦岭地区位于陕西省秦岭以西、甘南山地高原以东，甘肃、陕西、四川三省交界处(图1)，主体位于甘肃省陇南地区，面积约46 394 km2。全区海拔450～4 591 m，地势起伏大，近20年来曾多次出现大暴雨和特大暴雨，年降水量的80%～87%集中在4—9月，年平均暴雨1.5次，丰水年可达3～5次。

图1 西秦岭地区地理位置示意

1.2 研究数据

研究所需SRTM3-DEM数据下载自计算机网络信息中心国际科学数据镜像网站(http://datamirror.csdb.cn/)，经纬度栅格图层均由DEM提取，所有图层都采用相同的投影坐标系统。

气象站台经纬度、海拔及历年年平均降水量数据均来自中国气象科学数据网，时间段为1971—2000年，气象站台中分布于西秦岭地区的有23个，分布于邻近区域的有54个，总计77个(图2)。其中，考虑插值精度检验，随机选取气象站台总数的20%(14个气象站台)的降水量作为精度评估检验站点数据，其余80%的降水量作为实验站点数据。

图2 西秦岭地区气象站台空间分布

1.3 插值方法

1.3.1 反距离加权法(IDW法)

反距离加权法是基于相近相似的原理[3]，即两个物体离得越远性质就越不相似，反之，则相似性越高。计算时，以样本点与插值点间的距离作为权重进行加权平均，离插值点越近的样本点被赋予的权重越大。

1.3.2 综合插值法(改进后的多元线性回归法)

大尺度的降水与海拔、海陆相对位置有关[2]，因此海拔、经纬度等都可能影响降水量的分布。利用多元线性回归法进行区域整体插值，多元线性回归方程为

Y=a0+a1λ+a2Φ+a3h

(1)

式中：Y为多元线性回归模拟的降水量，mm；λ为经度；Φ为纬度；h为海拔；a0、a1、a2、a3为参数。

由于采用多元线性回归进行降水量插值模拟误差较大，不能区分不同区域的降水特征，因此将回归统计模型与插值模型相结合，即采用综合插值方法[10]进一步提高降水量模拟精度。选择IDW法插值结果与回归模拟结果分别作为两个影响因子，做二者与降水量实测值的多元线性回归，建立多元线性回归方程为

Y′=a0′+a1′I+a2′Y

(2)

式中：Y′为改进后的多元线性回归模拟的降水量，mm；I为用IDW法插值的降水量结果，mm；a0′、a1′、a2′为参数。

1.3.3 泛克里金法(UK法)

泛克里金法是以地理坐标X和Y的趋势面方程分离趋势项，再对分离漂移趋势项后的残差进行普通克里金预测[6]，最后将趋势面方程的预测结果与残差的普通克里金预测结果相加，泛克里金方法中的漂移趋势项是地理坐标X和Y的函数。

1.3.4 回归克里金法(RK法)

影响气候要素空间分布的地理因子可分为两类[11]：一类是大气候因素或宏观地理因子，例如大的山脉走向、地势高低和地理位置(经度、纬度和距海远近)等；另一类是小气候因素或微观地形因子，如地形遮蔽度、坡度、坡向和地形起伏量等。前者影响气候要素的空间分布趋势(称为宏观本底值)，可用经度、纬度和海拔3个变量来表述；后者影响气候要素的局地变化(称为小地形订正，即残差项)，可借助ArcGIS软件计算生成。使用公式可以表示为

P=F(λ，Φ，h)+ξ

(3)

式中：P为实测降水量，mm；λ为经度；Φ为纬度；h为海拔，m；F(λ，Φ，h)为降水的趋势值；ξ为残差项。

将F(λ，Φ，h)展开成三维二次趋势面方程为

F(λ，Φ，h)=b0+b1λ+b2Φ+b3h+b4λΦ+b5λh+

b6Φh+b7λ2+b8Φ2+b9h2

(4)

式中：b0，b1，…，b9为待定系数。

利用逐步回归优化模型，这种插值方法称为回归克里金法。

2 精度检验

采用交叉验证方法对插值结果进行对比分析，准确验证不同方法的相对精度。交叉验证法是先假定每一站点的降水量数值未知，用周围站点的数值来估算，再计算估计值与实测值的差值。本研究对14个检验站点(图1)的插值结果进行了交叉验证，采用平均绝对误差(MAE)、平均相对误差(MRE)、均方根误差(RMSE)作为评价指标，计算公式分别为

(5)

(6)

(7)

式中：n为检验站点数量；Pbi、Pai分别为第i个检验站点降水量的估算值和实测值，mm。

MAE值定量地给出误差，反映了估计值的实测误差范围。MRE能通过反映不同数据量或不同要素的误差相对值，定性地给出误差范围，效果更直观。RMSE值反映了利用样点数据估值的极值效应和灵敏度，其值越小模型越准确。

3 结果分析

3.1 降水量空间插值结果

本研究中将IDW法的站点搜索范围设为12，距离权重指数设为2，利用ArcGIS和SPSS软件得出基于IDW法、综合插值法的西秦岭地区多年平均降水量空间分布结果见图3(a)、(b)。

利用UK法进行空间插值时，西秦岭地区多年平均降水量三维二次趋势面方程为

F(λ,Φ,h)=-15 372.029+852.16Φ+3.644λ2-

20.541λΦ+2.249E-5h2+17.369Φ2

(8)

在对残差项ξ进行普通克里金插值时，模型和参数的选择可以影响到插值的精度，为了选择合适的模型、基台值、变程值等参数，利用GS+软件对残差数据进行了半方差分析。半方差分析显示球状模型效果最好，R2=0.958，块金值为770，基台值为7 111，变程值为242 300 m，偏基台值与基台值之比为89.2%，空间相关性强。最后将三维二次趋势面方程的预测结果与残差的普通克里金预测结果相加，得出多年平均降水量空间分布，见图3(c)。

利用RK法进行空间插值时， 相关性分析结果显示，经纬度与气象站台多年平均降水量、海拔之间均为极显著相关，表明西秦岭地区多年平均降水量的空间分布与空间位置(坐标)极显著相关。趋势面方程为

图3 西秦岭地区多年平均降水量空间分布

F=2 253.699-121.403Φ+23.936λ

(9)

式中：F为多年平均降水量趋势项；λ为经度；Φ为纬度。

由于研究区经纬度和海拔之间也存在极显著相关性，因此趋势面方程在一定程度上也考虑了海拔的影响。对残差进行分析得出最佳模型和参数，然后将趋势面方程的预测结果与残差的普通克里金预测结果相加，得出多年平均降水量的空间分布，见图3(d)。

3.2 误差分析

多年平均降水量空间插值交叉检验误差分析结果见表1。从表1可知，考虑了未知样本点的空间方位与已知样本点的空间分布关系的UK法、RK法的精度比IDW法、综合插值法高；RK法较UK法精度略高，但提高幅度并不大，RK法插值计算精度参数MAE=43.44 mm，MRE=7.4%，RMSE=57.35 mm。预测值与实测值的散点关系图如图4所示，其中RK法预测值与实测值之间的相关系数最大，为0.807 9。综合MAE、MRE、RMSE及相关系数的分析结果(表1、图4)，整体来看，各插值方法精度RK法>UK法>综合插值法>IDW法。这表明，在西秦岭地区利用RK法对多年平均降水量进行空间插值时，直接将海拔作为影响因子考虑进去，能够提高插值精度；在西秦岭地区，多年平均降水量的空间分布主要与空间位置(地理坐标)有关。

表1 不同插值方法精度比较

4 结 论

不同的插值方法对于不同地区、不同研究数据有其特定的应用范围。对比分析了常用的4种空间插值方法，分析得出西秦岭地区多年平均降水量空间插值方法的精度RK法>UK法>综合插值法>IDW法。

图4 4种插值方法实测值与预测值关系散点图

[1] 尚宗波,高琼,杨奠安.利用中国气候信息系统研究年降水量空间分布规律[J].生态学报,2001,21(5):689-694.

[2] 朱会义,贾绍凤.降水信息空间插值的不确定性分析[J].地理科学进展,2004,23(2):34-42.

[3] TSANIS I K,GAD M A.A GIS precipitation method for analysis of storm kinematics[J]. Environmental Modelling & Software,2001,16(3):273-281.

[4] WACKEERNAGEL H.Multivariate Geostatistics[M].Berlin:Springer-Verlag,1995:256.

[5] 邵晓梅,严昌荣,魏红兵.基于Kriging插值的黄河流域降水时空分布格局[J].中国农业气象,2006,27(2):65-69.

[6] 苏晓燕,赵永存,杨浩,等.不同采样点数量下土壤有机质含量空间预测方法对比[J].地学前缘,2011,18(6):34-40.

[7] SINGH V P,CHOWDHURY P K.Comparing some methods of estimating mean areal rainfall[J].Water Resources Bull,1986,22(2):275-282.

[8] 李新,程国栋,卢玲.空间内插方法比较[J].地球科学进展,2000,15(3):260-265.

[9] 赵传燕,冯兆东,南忠仁.陇西祖厉河流域降水插值方法的对比分析[J].高原气象,2008,27(1):208-214.

[10] 刘劲松,陈辉,杨彬云,等.河北省年均降水量插值方法研究[J].生态学报,2009,29(7):3493-3500.

[11] 林忠辉,莫兴国,李宏轩,等.中国陆地区域气象要素的空间插值[J].地理学报,2002,5(1):47-56.

(责任编辑 李杨杨)

江苏省高校自然科学研究面上项目(16KJB170014)

TP79

A

1000-0941(2017)06-0054-03

孙伟红(1986—)，女，山西运城市人，工程师，硕士，主要从事地理信息制图研究工作。

2016-11-15