基于Bayes统计理论的射表编拟方法

闫雪梅，文 艳，何 斌

（中国华阴兵器试验中心，陕西 华阴 714200）

基于Bayes统计理论的射表编拟方法

闫雪梅，文 艳，何 斌

（中国华阴兵器试验中心，陕西 华阴 714200）

全面系统阐述了Bayes统计理论下的射表编拟方法，具体研究了验前信息的处理、符合计算、编拟计算及试验用弹量的确定等几个关键难点问题，同时导出了确定先验分布中未知参数的计算公式、射表基本诸元的后验估计公式、射表试验用弹量的计算公式。通过两个实例对其具体使用方法给予了详细说明并对其结果进行了分析，指出应用该方法可以在相同精度要求下节省用弹量或在相同用弹量下提高射表精度，具有很好的经济适用价值。

先验分布，后验分布，射表编拟，样本量，Bayes

0 引言

射表是为打得准服务的，因此，如何编制高精度的射表始终是常规兵器试验技术领域中的一个重要课题。现行射表编拟方法是在多个仰角下进行射击试验，每个仰角射击m组，每组n发，试验后根据这些试验结果，按外弹道学理论编拟射表［1］。这种方法只考虑了本次试验结果即当前样本信息，没有考虑本次射击试验前的先验信息。然而，在编拟射表前存在有定型试验数据、临时射表试验数据等大量先验信息，这些信息较好地反映了武器系统的特性，合理准确地应用这些信息，可以在同一精度下减少正式射表试验用弹量或在相同用弹量下提高射表精度。问题是如何准确应用验前信息，按照Bayes观点，不能将验前信息和当前样本信息简单地“混合”在一起使用，那么，如何有效地利用验前信息编拟射表，笔者给出了一种应用Bayes统计理论的方法。

1 验前信息的处理

设X为在炮口水平面上炮口到落点的距离，X服从以μ，B2为参数的正态分布，这里的B在射表中称公算偏差，，ρ=0.476 9，σ是标准差。按Bayes观点，要把μ，B2看作随机变量，μ，B2的分布称为先验分布。验前信息的处理就是确定先验分布。为此，设B2的分布密度函数为π1（B2），μ的分布密度函数为π2（μ），则［2］

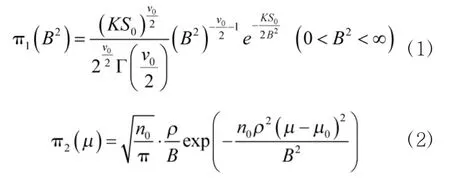
式中，K=2ρ2，n0为先验信息样本量，μ0，v0，S0为未知参数。按照Bayes理论，须应用验前数据获取这些未知参数。

假定在正式射表试验以前获得了准确可靠的定型试验、临时射表试验数据，在每一射角下有m组，每组n发，对每组进行射程标准化并将其平均，则得表载射程*，将试验所得各组公算偏差进行平均则得表载值，如表1所示：

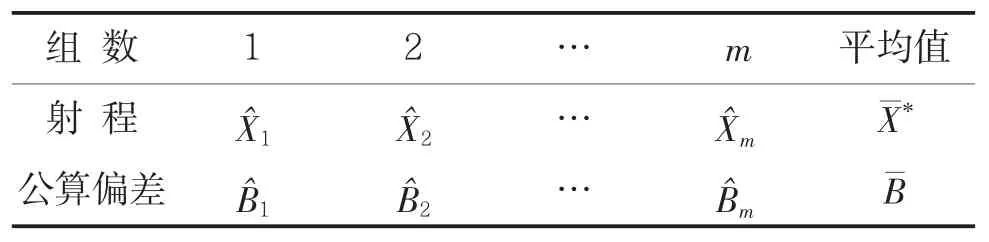
表1 验前信息数据表

由统计学理论知，表载射程X*是μ0的一个估值，因此，有

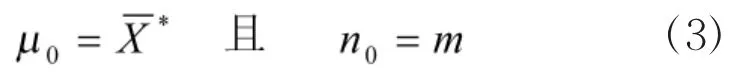
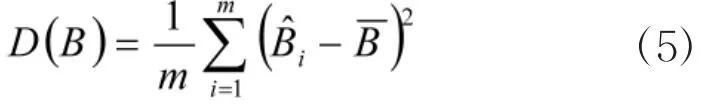
在文献［3］中作者详细讨论了式（5）的估计效果问题，指出只有当m较大时才有较好的估计精度，当m较小时将其修正为

由式（6）可以求出B2的方差为

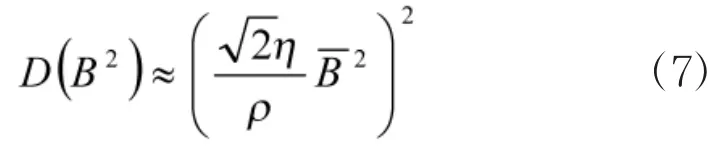
其中，η为巴尔坎系数（具体结果见文献［4］），这一结果被靶场使用至今。

另外，由式（1）有

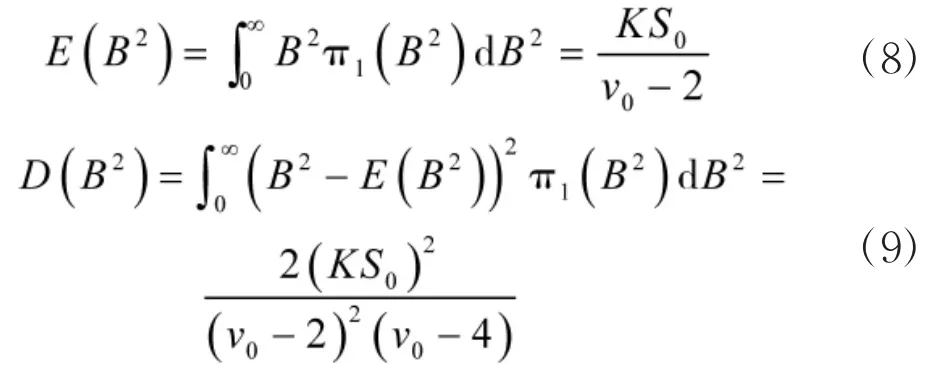
将式（8）、式（9）联立有

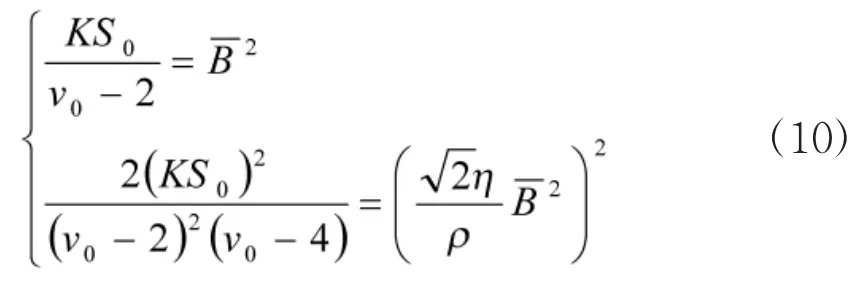
解式（10）即可求得未知参数v0，S0值。

至此，就完全确定了μ，B2的单个先验分布，由于μ，B2是相互独立的，因此，容易求出μ，B2的联合先验分布为

这一结果描述了验前试验数据的特征，包含了验前数据全部有用的信息。

2 基本原理

上述先验分布的确定为Bayes理论在射表编拟方法中的应用创造了条件。对给定的射角θi，假定本次射表试验标准化后获得的样本为，样本均值和样本离差平方和分别为

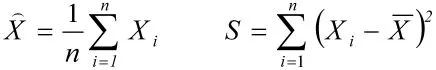
表2 当前信息数据表

表2即是编拟射表最基本的数据。当其他试验条件给定时，这些数据的精度取决于射表试验的样本量n。

为了进一步提高这些基础数据的精度，将验前信息融合到射表试验中，因为信息的增加等价于增加样本量。

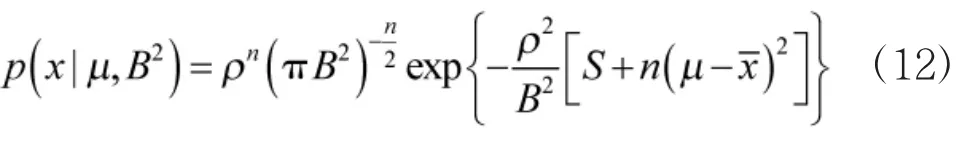
又由式（12）可以求出μ的后验边缘密度为

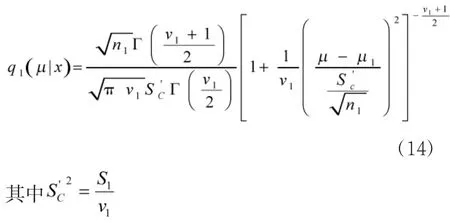
同样由式（12）可以求得B2的后验边缘密度为

依Bayes理论，μ，B2的后验期望估计为

由式（17）可得

即μ，B的估值为

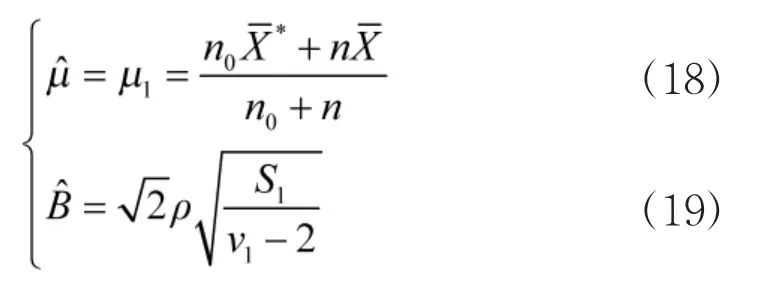
表3 验后信息数据表

这里特别强调，表3应用Bayes统计理论把当前的射表试验数据和历史数据融合成了一体。经典的射表编拟方法是以表2为基础数据的，现在可以将表3作为编拟射表的基础数据。显然，表3所含信息量大于表2的信息量，以此编拟射表必然在同一射表精度要求下，减少当前射表试验次数，或在相同试验次数下提高射表精度。

3 编拟方法

如何用表3的基础数据编拟射表需要解决的主要问题有以下几个方面。

3.1 符合计算问题

3.2 编拟计算问题

射表基本诸元和修正诸元的编拟计算基本上与现行方法相同，不同的是公算偏差需采用式（19）进行编拟计算。

3.3 用弹量的确定问题

射表试验前，首先要确定试验样本量，在Bayes统计理论下的射表用弹量与传统用弹量有所不同，那么如何确定Bayes统计理论下的射表用弹量？可从μ的后验边缘密度入手，依式（14），μ的后验边缘密度为

故变量的密度函数为

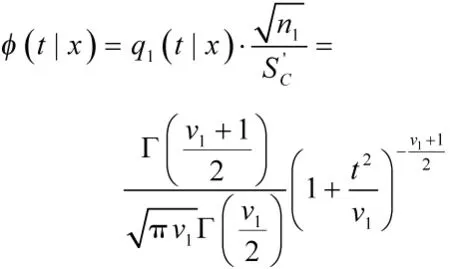
这恰是中心t（v1）分布的密度函数，即

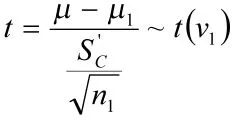
因此，给定可信水平1-α，以v1查t分布表得tα/2，使得

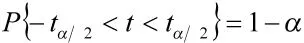
可得μ的可信水平为1-α的后验区间估计为

若给定双向规定的允许偏差量ε，则有

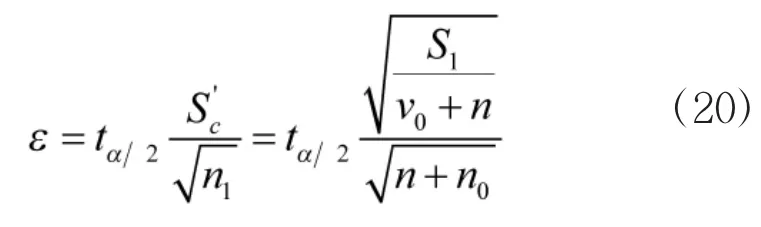
对式（20）求n，即可求得确定用弹量的计算公式

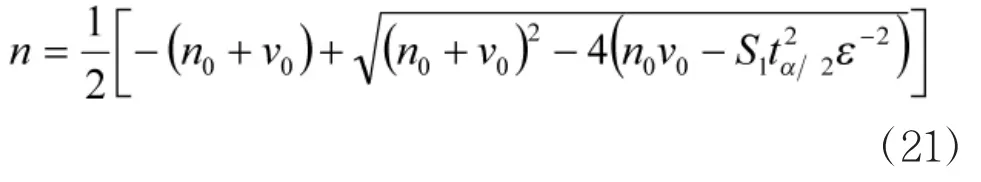
事实上，n0为验前信息样本量，可由历史资料中获取，v0已由式（10）求出，S1可由验前密集度等试验数据估计，依文献［1］，，对普通榴弹，另外，tα/2未知，可先给出一近似值，由“试差法”调整tα/2值求样本量n。

至此，应用Bayes理论编拟射表的基本问题已全部解决，其他则和传统射表编拟的做法完全一致，这里不再赘述。

4 实例与分析

下面给出两个实例，说明在Bayes统计理论下射表中最基本诸元射程、公算偏差及用弹量的计算方法，并对其结果给予分析。

例1从某榴弹炮定型试验结果中得θ0=30°时，纵向公算偏差为X=35，试验验本量为N=12，标准化射程为*=10 200，今正式射表试验共3组，每组7发，总用弹量为n=21，求得离差平方和为S=70 337，平均标准化射程为=10 250，按Bayes方法求射表中的基本诸元射程XN及公算偏差BX。

解：①求S0，v0

依式（10）有

依式（19）得BX=43.2

在射表中，最重要的诸元是XN，射表精度主要是指XN的精度。现对XN的表达式两边求方差得

故采用Bayes理论后，将原射表精度由0.3%提高至0.233%，即精度提高约22%。

由于验前信息量在每一试验中是不同的，因此，精度的提高是随验前信息量不同而变化的，应具体情况具体分析。

例2从某加农炮配杀爆榴弹的定型试验结果中得θ0=35°时，n0=14，*=25 000，X=63，今拟编拟正式射表，求用弹量n。

解：先求v0，S0，依题意有

解得v0=8 S0=52 353.7

对加农炮配榴弹，精度要求为［1］

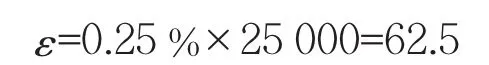
故

显然，当在同一射表精度要求下，即精度要求为0.25%X时，按原来的方法需射击21发，当采用Bayes理论后，只需射击9发即可，节省弹药57%。

5 结论

全面系统地阐述了Bayes统计理论下的射表编拟方法，详细讲述了应用该方法需解决的几个难点问题：①验前信息的处理；②符合计算方法；③编拟计算方法；④用弹量的确定方法。

该方法由于应用了验前信息，扩大了数据量，从而达到了在相同精度要求下节省用弹量或在相同用弹量下提高射表精度的目的，有很好的经济适用价值和推广应用价值。

［1］闫章更，祁载康.射表编拟技术［M］.北京：国防工业出版社，2000.

［2］闫雪梅，文艳，邱丛礼.射程与密集度分组试验的Bayes估计［J］.弹道学报，2006，18（2）：80-83.

［3］茆诗松.贝叶斯统计［M］.北京：中国统计出版社，1999.

［4］巴尔坎（苏）.弹药靶场试验法［M］.北京：总后勤部军械部，1956.

Compilation of Firing Tables Methods Based on Statistical Theory of Bayes

YAN Xue-mei，WEN Yan，HE Bin
（China Huayin Ordnance Test Center，Huayin 714200，China）

The compilation of firing tables methods based on statistical theory of Bayes is elaborated comprehensively and systematically.Several key challenges are studied detailedly，including dealing with prior information，fitting computation，compilation computation and determining the projectile consuming number，and the formulae are deduced to solve the unknown parameters of the prior distribution estimations，the posterior estimation of the firing table basic parameters，the projectile_consuming in the firing table test.The specific usages are demonstrated in detail by two examples，its results are analyzed.Results show that test ammunitions can be reduced under the same accuracy or the compilation of firing tables accuracy can be improved under the same test ammunitions by the method created in this paper，with strong economy serviceability.

prior distribution，posterior distribution，compilation of firing tables，sample size，Bayes

TJ012.3

A

1002-0640（2017）05-0121-05

2016-03-16

2016-05-18

闫雪梅（1968- ），女，陕西白水人，硕士，高级工程师。研究方向：外弹道及数理统计。