浅析经济管理决策分析方法之层次分析法

焦莉萍

摘要：本文通过对层次分析法的应用实例的研究分析，介绍了层次分析法的优缺点及其具体操作步骤，即建立递阶层次结构、构造判断矩阵、计算权重向量、一致性检验，得出了层次分析法是定量与定性方法相结合的优秀的决策方法，不仅原理简单，而且具有扎实的理论基础，也可以解决定性因素起主导作用的决策问题。

关键词：层次分析法；递阶层次结构；判断矩阵；权重

层次分析法是一个系统，这个系统的整体可能十分复杂、难以解决，但我们可将其分为各种准则或目标，再将这些准则或目标分成更细的部分，从中区分出不同的层次，再以特定的方法进行测算和评估，最后根据评估分析的结果做出相应对策来优化整体。其应用过程与人对一个复杂的决策问题的思维、判断过程大概是一致的。在我们做出一个决策前，往往要对此决策牵扯的各方面进行思考与分析，从而决出哪个方案是对我们最有利的。层次分析法就是这样一个方法。它需要你先将决策问题分为几个方面，而这几个方面恰好是决策问题的关键。通过对这些方面所占权重进行分析，结合某方面对另外一方面的优先比重，最后再用加权和的方法求出对总目标的最终权重，即决策的最佳方案。

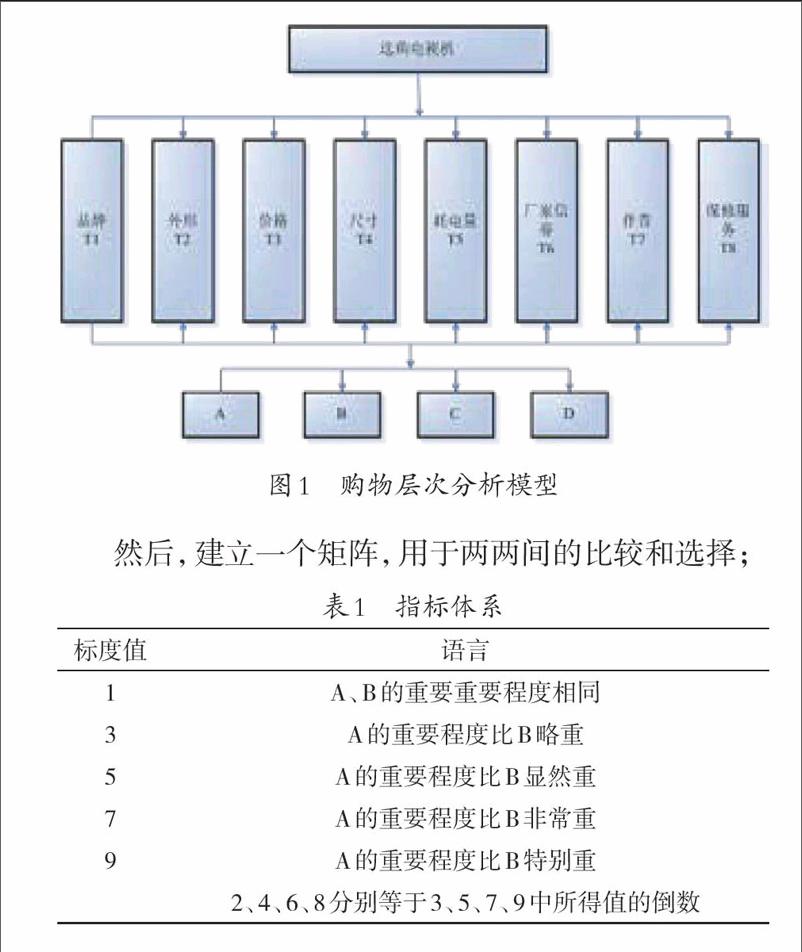
1层次分析法应用实例

首先，构造一个递阶的层次结构；

最终，依据特定的规则，确定各备选元素在系统总体中所占的权重；

一般来收，有两个确定矩阵权重的规则：几何平均法及规范列平均法，又叫做根法与和法。

（1）几何平均法（根法）

按行求元素乘积，即同一行的各个元素相乘，得到一个n行一列的矩阵B；

将矩阵中的所有元素都开m次方根得矩阵c；

将上述求得的结果归一化得矩阵D；

最终得到的矩阵就是为我们需要求的权重向量。

（2）规范列平均法（和法）

矩阵A每一列归一化得到矩阵B；

将矩阵B每一行元素的平均值得到一个一列斫亍的矩阵C；

矩阵C即为所求权重向量。

2层次分析法的优缺点

2.1优点

2.1.1系统性的分析方法

系统性思想中最重要的一点就是不片面、孤立的而是从一个整体、全局的角度来分析所有不同因素对于最终结果的影响；在层次分析法的应用过程中，最终的结果不可避免的会受到不同层次中不同因素所占权重安排的影响，而针对这些影响我们可以通过特定的方法进行量化，使其更易于比较和分析。层次分析法概括来说就是：先分解，然后比较判断，最后综合分析。系统分析，即研究对象是作为一个系统出现的这样一种分析方法，在层次分析这一工具出现以后，取得了进一步的发展。

2.1.2简洁实用的决策方法

层次分析法基本原理及步骤易于掌握，计算起来十分简单方便，结果也一目了然、明确具体，在决策过程中提供了极大的便利。这种方法把定性方法与定量方法有机的结合起来，使人非常容易接受，并且在确定不同层次的数量关系的基础上，采用简单、方便的计算。这样便将问题从多个目标、多个准则转化为一个更易于解决的多层次单目标问题。

2.1.3定量数据信息需求较少

作为一种思维方法的模拟，要素的权重并非由层次分析法本身决定，而是由大脑去实现这个过程，只留下要素的印象在大脑中，从而简化运算。它更注重于发掘问题的本质，相对其他定量方法来说更侧重定性分析，因此在研究过程中，它所需的定量数据信息也比较少。这样看来，这种思想为日常生活提供了不可思议的好处——很多的无法利用经典的最优化技术解决的问题得到了答案。

2.2缺点

2.2.1不能为决策提供新方案

在大部分决策者的眼中，完美的分析工具的定义，或者说其作用力体现在：能够帮助我们从所有可行方案中找出最优的方案，还可以向我们说明各种方案中所存在的缺点，并在此基础上提出意见建议帮助我们对方案进行完善。无疑，层次分析法并不能胜任这些要求。比方说使用过程中，经常遇见以下情形：因为创造力的缺乏，即便是从所有我们能够想得到的方案中选择了最优的一个，然而成效与企业做出来的相比较，从效果来看，仍有较大的差距。由已知情况来看，层次分析法是从所有可供选择的方案中取一个相对较好的方案，这恰恰表明了层次分析法并不能得到新的更优的解决办法，而只能在已有的方案中选出最好的一个。

2.2.2定性成分多，定量数据较少，难以令人信服

层次分析法从模拟人脑出发，其应用也就无可避免的较大程度上依赖定性思维；而在一门科学需要比较严格的数学论证和完善的定量方法是如今对科学方法的评价中最为常见的。大部分情形下，使用数字并不能解释实际存在的诸多问题及大脑在思考过程中出现的诸多想法，如此，那么如果有人通过层次分析法来进行决策的话，就会有人质疑其方法的科学性和准确性。

一个比较简单的例子就是，笔者认为舒适和耐用是评价服装的主要指标，但是女性对衣服的评价一般是美观度是最主要的，因此笔者所认同的指标对于女士们来说，估计是比较难接受的，因为，她们通常来说并不在意服装是否耐用，有些时候可以说是完全不在意，有些衣服可能就算只能穿一次，在她们看来也是十分值得的。如上，像这样的本来是分析服装的评价指标的研究，最多也只能说是男性关于服装评价相关指标的研究。当定性的东西比较多时，这样一个研究可以解决问题的范围相对来说就会变小。而前面所说的难题并不是没有办法解决。例如，将美观度加入进去，便能在很大程度上弥补笔者的评价指标过少的问题，在这种情况下很多问题可以很好解决，不停地增加指标嘛！但是，需要考虑的问题是，指标是越多越好吗？毫无疑问，衡量问题的尺度如果太多，决策可能更不容易做出。

2.2.3指标过多时较大的数据统计量，以及难以确定的权重

在研究问题的过程中，我们往往通过寻求以增加指标数量的方式来解决。这就和系统结构理论中的情形很相像了，要分析系统结构，就要搞清楚关系环节，就要深入分析到基层次。也正是由于这个原因，随着越来越多的指标、越来越深的层次、越来越多的数量还有越来越大的判断矩阵有了更为深重的意味。在这种情况下，对许多的指标进行两两比较的工作也显得十分重要。有时候，会出现这样一种情况，判断矩阵得到的特征向量并非合理。并且会有这样的弊端，随着不断加多的指标数量，指标与指标间的重要性就变得更难以判断，还会使层次单排序和总排序的一致性受到干扰，导致一致性检验最终可能无法得到预期的结果。换句话说，不能通过，就需要调整，由于思维定式，当认为哪个指标越重要时就会觉得其越难以调整，那么也就难以发现问题所在。尤其在指标数量多的时候，调整算得上是个很痛苦的过程，而且花费了时间，却无法通过检验，更糟的是完全不知道问題所在。也就是判断矩阵中是哪个出问题的元素没有办法被指出来。

2.2.4比较复杂的特征值和特征向量的精确求法

二阶、三阶并不难，不过阶数也会依指标的增加不断增加，计算难度也就越来越大。但是，问题的解决不是特别复杂。通常有以下三种近似计算的方法：和法、幂法和根法。另外，所用的方法和我们多元统计所用的方法一样的情况也会出现，例如求判断矩阵的特征值和特征向量。

3层次分析法的使用过程

3.1创建递阶层次架构。

3.1.1最高层：即目标层。

3.1.2中间层：用以达到目标所能采取的方式方法所包含的中间环节；或者为了在各个待选方案中作出决策，用来评价各待选方案的各方面评价指标，包括准则层、指标层等。

3.1.3最低层：具体解决方式方法，也即可实施的方案。

每层有若干元素，层间元素的关系用相连直线表示。例如在进行风险投资决策的问题中，对于经济管理过程中风险投资公司来说，一般情况下，此决策问题的进行步骤可安排如下，将分解决策为三个层次，

（1）目标层——合适的投资方案的选择；

（2）准则层——进行分析操作：风险分析、成长分析、社会政治影响分析、环境影响分析、市场评估因素分析、产品技术分析、财务分析、经济政策影响分析与行政环境分析等；

（3）方案层——产生n个待选择决策方案并将各层次用直线连接。

3.2构造判断矩阵

根据准则，将方案进行两两对比，按其重要性评定等级，以两两重要性程度之比的形式表示两个方案的相应重要性程度等級，记为两个因素的重要程度的比值，表1列出给出的重要程度的比较和值的大小。判断矩阵指的是按两两比较结果构成的矩阵。判断矩阵的性质具体如下式所示：

其次，求权重向量的值。

定义：判断矩阵若有以下简单性质，那么可以说符合一致性。

（1）具有唯一的非零特征值，其对应的特征向量归一化后叫做权重向量；

（2）各列向量之和经规范化后的向量，就是权重向量；

（3）任一列向量经规范化后的向量，就是权重向量；

（4）全部列向量求每一分量的几何平均，再规范化后的向量，就是权重向量。

3.3一致性检验

判断矩阵的阶数比较高的时候，往往需要很费力气才能构造出满足一致性的矩阵。但判断矩阵偏离一致性条件又必须在一个可以把握的范围内，正是由于这个原因，我们要分析判断矩阵能不能接受，以上即为判断矩阵的含义。

（1）随机的原因可能会造成的一致性的偏离，所以分析判断矩阵是否具有满意的一致性的检验过程中，也要比较C与平均随机一致性指标彤，求出检验系数CR，CR的值与一致性的大小成反比。

（2）以上判断矩阵能不能得到预期的一致性的一个重要参考便是CR，如果CR<0.1，则认为其通过，反之，就不具有满意一致性。

由以上可见，层次分析法方法是定量与定性方法相结合的优秀决策方法，不仅原理简单，而且具有扎实的理论基础，也可以解决定性因素起主导作用的决策问题。