基于潮流解存在性的微网电压稳定判据研究

沈 方，张明理，商文颖，梁 毅，高 靖

(国网辽宁省电力有限公司经济技术研究院，辽宁 沈阳 110015)



基于潮流解存在性的微网电压稳定判据研究

沈 方，张明理，商文颖，梁 毅，高 靖

(国网辽宁省电力有限公司经济技术研究院，辽宁 沈阳 110015)

针对微网的网架结构和运行特点，根据潮流解的存在性推导了一种适用于微网的静态电压稳定指标。该指标考虑了节点电压的影响，且不受网络R/X值限制；另外其在推导过程中不需进行网损等值，因此误差较小。搭建了13节点微网系统，验证了推导指标的正确性，最后利用该指标分析了PV、PI、P-Q(V)3种节点类型的分布式电源及其位置和容量对微网静态电压稳定性的影响。

微网；电压稳定指标；分布式发电；电压稳定性

近年来，微网相关课题已成为电气工程领域的研究热点之一。目前主要集中在微网并网对传统电网的影响以及微网自身的建模和运行控制方面，有关微网节点电压稳定性的研究相对较少[1-8]。由于微网是多种基于电力电子技术的分布式电源的集合，因此不具有传统电网的惯性特征，微网并网运行和孤岛运行的切换难免对其内部的电压造成冲击，除此之外，由于微网含有大量的间歇性能源如风力发电和光伏发电等，其运行特性受自然因素的影响比较大，难于控制。因此，微网的电压稳定问题相较于大电网更为复杂。

微网的网架结构和配网相似：辐射状、R/X比值大、分支多。因此微网的电压稳定研究方法可在配网电压稳定研究方法的基础上加以改进。配网的电压稳定性判断方法大致可分为两大类，根据潮流计算中解的存在性判断法和根据负荷—电压特性判断法。前者最早由文献[9]提出，文中推导了两节点的配网电压稳定性指标，并通过定义等效阻抗等方式将该指标推广应用于多节点的配网。但是在推导过程中，从网损等值的角度将复杂配电系统等值成简单的两节点系统，误差较大并且没有考虑节点电压对电压稳定性的影响。文献[10]在简单系统中推导了一种基于V-I特性的节点电压稳定快速判断方法，并成功应用于复杂系统，但该指标并不严格，不适合负荷较重或线路阻抗较大的情况。

本文根据潮流计算中解的存在性判断法，在配网电压稳定指标的基础上加以改进，推导了一种适用于微网电压稳定的指标，建立了13节点微网系统，验证了指标的正确性，并利用该指标分析了PV、PI、P-Q(V)3种节点类型的分布式电源及其位置和容量对微网静态电压稳定性的影响。

1 基于叠加原理的改进Zbus潮流算法

潮流计算是研究基于潮流解存在性的电压稳定指标的基础。微网的网架结构与传统的配电网相似，但其潮流计算又与配网潮流计算有所不同。微网不但包含传统配网中常有的Vθ和PQ节点，还包括各种非常规节点如PI、P-Q(V)等。配网潮流计算大致可分为牛顿拉夫逊法、前推回代法和直接法3类。牛顿法对电压初值非常敏感，在配网计算中收敛性较差；前推回代法面向单电源的辐射状网络，但不能有效处理弱环网；直接法又称Zbus或Ybus法，它基于节点电压的迭代计算，该法具有较强的处理弱环网能力，而且适合处理具有电压静态特性的节点类型，但是对含PV节点的网络则不能有效处理。

由于微网R/X值较大，末端电压通常较低，因此对初值敏感的牛顿方法不适用于微网；另外，微网中常有弱环网，所以前推回推法也不适用。综上考虑，本文选择直接法来计算微网潮流，并提出了基于叠加原理的改进Zbus算法，使用补偿技术解决了传统Zbus算法无法处理PV节点的问题。具体步骤如下。

a.输入网络的原始数据，形成微网的导纳矩阵。

b.给定节点电压初值，设静态电压特性节点、PQ节点电压初值U(0)=1，PV节点无功Q(0)=(Qmax+Qmin)/2。设迭代次数s=1。

c.求出相应的节点电流，利用线性方程组的三角分解法求出只与负荷、微电源节点及接地支路作用有关的各节点电压，进而求得各节点电压。

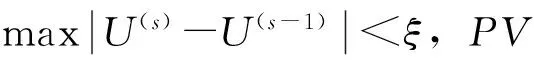
e.输出计算结果，结束。

2 基于潮流解存在性的微网电压稳定判据

对于含有N节点的微网，其中可以包含分支线路和补偿电容器，设其任意一条支路为Lij，其中i和j分别为该支路的2个节点，潮流方向为从节点i流向节j点 ，即i为支路潮流送端，j为支路潮流受端。支路Lij的阻抗为Rij+jXij，流过节点j的负荷为Pj+jQj，则有：

(1)

式中：Ui和Uj分别为直角坐标形式的节点i和j的电压向量。由式(1)可得：

(2)

UX,j=[UR,jUX,j-(PjXij-QjRij)]/UR,i

(3)

式中：UR,i和UX,i分别为Ui的实部和虚部，UR,j和UX,j分别为Uj的实部和虚部。将式(3)带入式(2)可得：

(4)

(5)

要保证微网的电压稳定，式(4)和式(5)应有实数解，其一元二次方程式的根判别式应大于或等于0，即：

(6)

式中：Ui是Ui的模。

定义支路Lij的静态电压稳定指标为Kij，则有：

(7)

式(6)可写成：

Kij≤1

(8)

从推导过程可知，Kij越小，系统的电压稳定性越好；Kij越大，系统电压稳定性越差。因此对于整个微网来说，评价微网电压稳定性的指标为

K=max{Kij}

(9)

对应K的支路被称为系统的最薄弱支路，一般认为从最薄弱支路开始引发系统发生电压崩溃，因此将电压稳定裕度定义为K值与临界值1.0的距离，并用之来判断系统电压稳定的程度。

3 算例分析

本文将式(9)作为微网静态电压稳定性指标的计算公式。根据前面推导的公式在Matlab中编程，实现微网的潮流求解和电压稳定指标计算。在PSCAD中搭建了13节点微网系统作为分析对象，该系统不考虑三相不平衡情况，单线图如图1所示。1节点电压标幺值为1.0，设置为平衡节点，4节点为PV节点，容量为20 MW，其它节点均为PQ节点，负荷均为恒定负荷，潮流算法的收敛精度取为0.000 01。

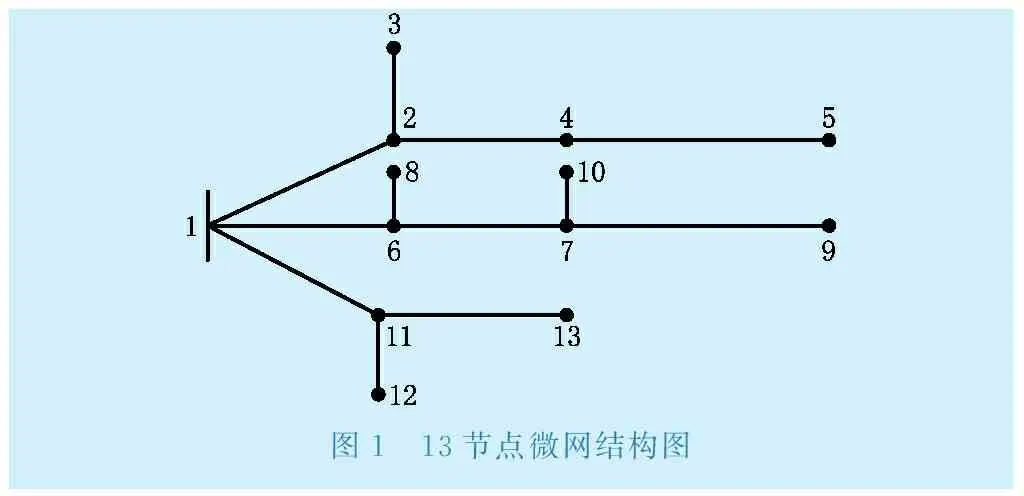
图1 13节点微网结构图

首先验证本文推导指标的正确性，在13节点微网系统不接入任何外来分布式电源的情况下，利用本文方法的Matlab编程计算其静态电压稳定指标K，与PSCAD中模型仿真结果进行对比如表1所示。

表1 指标正确性的验证

从表1可以看出，两者的误差不到0.5%，因此指标K具有较高的可信度。下面将分别研究分布式电源的类型、位置和出力对微网静态稳定性的影响。

3.1 不同类型电源对微网静态电压稳定性的影响

为测试不同类型的分布式电源对微电网静态电压稳定指标K的影响，在13节点系统的10节点上依次安装3种不同类型的分布式电源：容量均为10 MW的电压控制型微型燃气轮机DS1、电流控制型光伏发电系统DS2和小型风力发电机组DS3，分别把它们作为PV节点、PI节点和P-Q(V)节点来处理，用潮流计算程序依次对该系统的3种状态进行计算达到收敛，计算出3种不同类型分布式电源并入微网运行后的静态稳定电压指标K，结果如表2所示。

表2 不同类型电源对K的影响

由表2中数据可以看出，接入分布式电源DS1和DS2时系统静态电压稳定指标与没有外来电源时相比变小，说明这2种分布式电源有利于改善静态电压稳定性指标，提高微网的电压稳定性；而DS3接入微网后，静态电压稳定性指标有所增大，表明微网电压稳定性下降。这是因为异步发电机需要吸收来自系统的无功功率。为了减少异步单元对系统的不良影响，在实践中，通常需要安装能够在与微电网的公共耦合点自动切换的电容器组。

3.2 出力变化对微网静态电压稳定性的影响

为测试分布式电源出力变化对微网的静态电压稳定指标K的影响，在10节点上分别安装不同容量的电压控制型微型燃气轮机DS1，依次为10 kW、30 kW和50 kW。用微网潮流计算程序依次对这3种情况进行计算，达到收敛，得出静态电压稳态指标如表3所示。

表3 不同电源容量对K的影响

由表3数据可知，随着分布式电源输出功率的不断升高，微网系统的静态电压稳定性指标先减小后增大。即微网中适当增加分布式电源的输出功率可以有效改善系统的电压稳定性，但输出功率过大微网系统电压稳定性将会变差。

3.3 位置变化对微网静态电压稳定性的影响

微网中分布式电源的分布位置变化，也可能影响系统的静态电压稳定性。分别将3种电源DS1、DS2、DS3安装在6、7、8节点上，对微网系统静态电压稳定性指标的影响如表4所示。

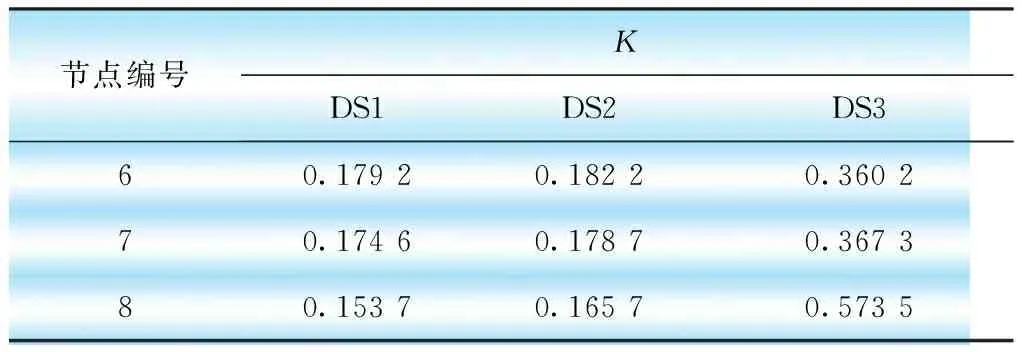
表4 不同电源位置对K的影响

由表4数据可知，DS1和DS2安装位置越靠近系统的最薄弱支路，微网静态电压稳定指标K越小，越有利于改善微网系统的静态电压稳定性。而对于DS3，安装位置越靠近系统最薄弱支路时，静态电压稳定指标越大，越不利于提高系统静态电压稳定性，离系统最薄弱支路越远对系统电压稳定性的负面影响越小。

4 结论

本文针对微网的网架结构和运行特点，根据潮流解的存在性推导了一种适用于微网的静态电压稳定指标。搭建了13节点微网系统，利用推导指标分析了PV、PI、P-Q(V)3种节点类型的分布式电源及其位置和容量对微网静态电压稳定性的影响，得出以下结论。

a.电力电子接口分布式电源，如微型燃气轮机和光伏发电以及其它的PV、PI型电源，具有较好的控制特性，可减小微网静态电压稳定指标，改善微网系统的静态电压稳定性，且系统最薄弱支路与并网位置越靠近，对系统静态电压稳定性的改善程度越显著。

b.风力发电机采用异步发电机接入电网时，将会从系统吸收无功功率，导致系统静态电压稳定指标变差，影响微电网的电压稳定，且系统薄弱支路离并网位置越近其负面影响越大；其它的P-Q(V)型电源也有类似的特性。

c.在微网的分布式电源规划过程中，可以让具有异步发电机模型的分布式电源尽量远离系统中较薄弱支路，其它接口分布式电源类型可以尽量靠近薄弱支路。

[1] 杨仁花，黄 伟，关 丽，等. 微网结构和运行控制[J]. 智能电网，2010，26(1)：48-55.

[2] 赵 波，李 鹏，童杭伟，等. 从分布式发电到微网的研究综述[J]. 浙江电力，2010，29(3)：1-5.

[3] 王志霞，张会民，田 伟. 微网研究综述[J]. 电气应用，2010，29 (6)：76-80.

[4] 丁 明，张颖媛，茆美琴. 微网研究中的关键技术[J]. 电网技术，2009，33(11)：6-10.

[5] Piagi P，Lasseter R H．Control and design of microgrid components [R]．USA：Power Systems Engineering Research Center，2006．

[6] Driesen J，KatiraeiF．Design for distributed energy resources[J]．IEEE Power and Energy Magazine，2008，6(3)：30-39．

[7] 卢 芸，白钦予，路 昱，等. 一种微网静态电压稳定判别指标研究[J]. 东北电力技术，2014，35(5)：1-6.

[8] 苑 舜，刘志武. 基于分散式风储提高电压稳定性的虚拟电厂研究[J]. 东北电力技术，2014，35(10)：1-4，26.

[9] G．B．Jasmon，L．H．C．C．LEE．Distribufion network reduction for voltage stability analysis and load flow calculations[J]．International Journal of Electrical Power&Energy Systems，1991，13(1)：9-13.

[10] 李宝国，鲁宝春，巴金祥. 一种基于V-I特性的节点电压稳定快速判断方法[J].继电器，2004，32 (11)：1-4.

Research on Voltage Stability Index for Microgrid Based on Power Flow Solution Existence

SHEN Fang，ZHANG Mingli，SHANG Wenying，LIANG Yi，GAO Jing

(State Grid Liaoning Electric Power Company Limited Economic Research Institute, Shenyang，Liaoning 110015, China)

In allusion to the grid structure and operation characteristics of microgrid,a static voltage stability index for microgrid is deduced based on the existence of the power flow.The index has taken the node voltage into account and is free from the influence of the grid’sR/X; besides, it has a smaller error for no network loss equivalent during its deduction.Then one 13-node microgrid system is established to validate the deduced index,finally the index is used to analyze the influences of distributed sources including thePV、PI、P-Q(V) node types as well as heir locations and capacities on the static voltage stability of microgrid.

microgrid;voltage stability index; distributed source;voltage stability

TM76

A

1004-7913(2017)05-0014-04

沈 方(1963)，男，学士，高级工程师，研究方向为电力体制改革与电力系统规划。

2017-03-01)