过三点如何作多面体的截面

华南师范大学附属中学(510630) 罗碎海

过三点如何作多面体的截面

华南师范大学附属中学(510630) 罗碎海

目前流行的高考二轮复习资料《创新设计》P36【例1-2】:如图,在棱长为6的正方体ABCD−A1B1C1D1中,E,F分别在C1D1与C1B1上,且C1E=4,C1F=3,连接EF,FB,DE,BD则几何体EFC1−DBC的体积为( )

A. 66 B. 68 C. 70 D. 72

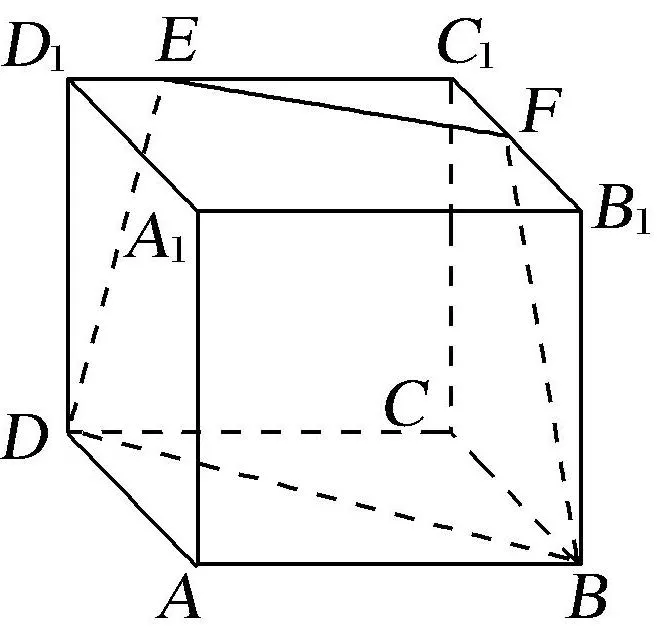
图1

这是一道错题,点E、F、B、D四点不在同一面内,无法求体积．但书中给出答案,而且有些学生也做出答案A．由此可见,无论是做题人还是制题人都在立体几何作图问题上有所欠缺,该问题值得研究．

在平面几何中,尺规作图是妙趣横生、引人入胜、很有思维挑战的一类问题,特别是几何作图三大不能问题(三等分角;立方倍积;化圆为方)更是登峰造极之题,引无数英雄竞折腰,大大推动了数学的发展．而在立体几何中因存在诸多不便,作图问题就不作为主要问题来研究,但画空间几何体的截面也是一件很有意义之事．虽在高考考试中,对立体几何作截面的要求不高,考试说明中明确指出:只要求会画出给出全部顶点的多面体截面．但对于立体几何的学习,作图问题(画截面)是概念、定理深刻理解与应用的基本标志之一,更是培养学生空间想象能力及创造性思维能力的不可多得的素材．

由于不在同一直线上的三点确定一个面,所有问题就归于已知三点画截面.画截面就是找到截面与多面体的面的交线,找交线就是找到同一面上两个点．所以作截面常用的根据是以下6个定理或公理:

(1)(公理)同一平面内的两条直线,若不平行必然相交．

(2)(公理)如果一条直线上的两点在一个平面内,则这条直线在这个平面内．

(3)(公理)两个平面如果有一个公共点,则它们有且只有一条通过该点的公共直线．

(4)(定理)过两平行线或两相交直线有且只有一个平面．

(5)(定理)三个平面两两相交,它们的交线或交于一点或两两平行．

(6)(定理)两个平行平面与第三平面相交,则它们的交线平行．

具体的方法思路有:直接连线,延长线段,作平行线,作辅助面等．有时可能需要射影,有时还可借助代数特别是向量来计算．以下我们从最简单的多面体—长方体为主分析各种情况并总结其方法．

一、已知三点在长方体的棱上的情况

问题1.1已知三点分别在长方体三条棱上,三棱为顺次相交的长、宽、高,如何作过此三点的截面?

例1 长方体ABCD−A1B1C1D1,P、Q、R分别为D1A1、A1A、AB上任意一点．作出过点P、Q、R的平面α截长方体ABCD−A1B1C1D1的截面．

分析同一面上两点连线延长与棱相交,连续进行．

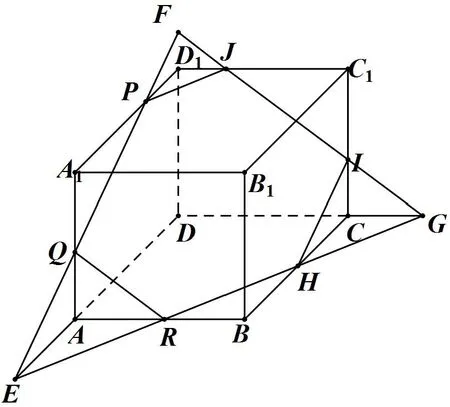
图2

作法如图2,连PQ,交DD1、DA延长线于F、E;连E、R交BC、DC延长线于H、G;连F、G,交D1C1、C1C于J、I;连PQRHIJP为所作截面．

(说明:截面有可能是三角形、四边形、五边形、六边形)

评述面上有两点,连线就是交线．

问题1.2 已知三点分别在长方体三棱上,其中有两棱相交,如何作过此三点的截面?

例2 长方体ABCD−A1B1C1D1,P、Q、R分别为C1D1、A1A、AB上任意一点．作出过点P、Q、R的平面α截长方体ABCD−A1B1C1D1的截面．

图3

作法如图3,连RQ,交B1A1延长线于E;连E、P交A1D1延长线于F;连F、Q,交DA延长线于G;连G、R交BC、DC延长线于H、I;连I、P交CC1于J;连PFQRHJP为所作截面．

评述点为两线相交所得,线为两面相交所得,这样认识例1、例2思想方法相同．以上作图主要用到定理(1)、(2)、(3)．

问题1.3 已知三点分别在长方体的三条棱上,三棱相互异面,如何作过此三点的截面?

例3 长方体ABCD−A1B1C1D1,P、Q、R分别为D1A1、AB、CC1上任意一点.作出过点P、Q、R的平面α截长方体ABCD−A1B1C1D1的截面．

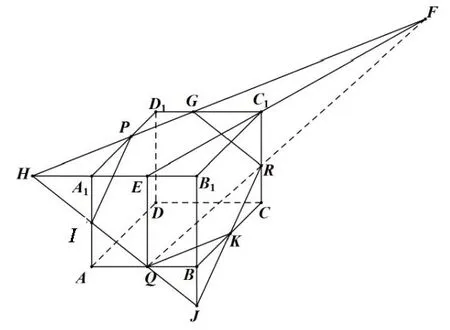
图4

作法如图4,作QE//BB1交A1B1于E,则QE、RC1确定一个平面;连EC1,QR交于点F;连FP交C1D1、B1A1延长线于G、H;连HQ交A1A、B1B延长线于I、J;连JR交BC于K．连KRGPIQK为所作截面．

评述本作法用到定理(4)、(5),关键是由Q、R找到点F,使点F与点P在同一面内(过点Q、R作点P所在面的垂线)．反思两个问题:

①若作QE//AD交DC于E,下一步如何作?

②若作PE//AA1交AD于E,下一步如何作?

问题1.4 (特殊问题)已知三点分别在长方体的共顶点的三条棱上,如何作过此三点的截面?

答直接连每两点,得到的三角形就是截面．

问题1.5 (特殊问题)已知三点分别在长方体的三条互相平行棱的上,如何作过此三点的截面?

答直接连线,作平行线即可．(用到(5)、(6))

问题1.6 已知三点分别在长方体的三条棱上,其中只有两条棱平行,如何作过此三点的截面?

(平行棱上两点连线,仿例1,略)

二、已知三点不在长方体棱上而在表面上的情况

问题2.1 三点在长方体的共顶点的相邻的三个面上,如何作过此三点的截面?

例4长方体ABCD−A1B1C1D1,P、Q、R分别为面ABB1、BCC1、A1B1C1上任意一点．作出过点P、Q、R的平面α截长方体ABCD−A1B1C1D1的截面．

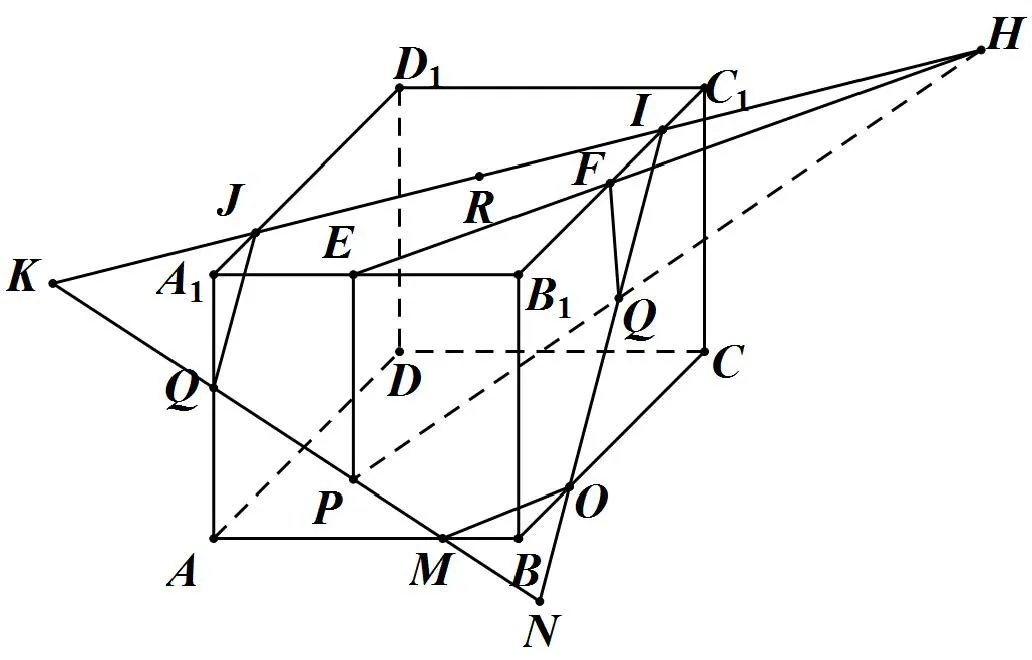
图5

作法如图 5,过P作PE⊥A1B1于E,过Q作QF⊥B1C1于F,连EF、PQ交H,连HR交B1C1、D1A1、B1A1于I、J、K,连KP交A1A、AB、B1B延长线于L、M、N,连NI必过Q与BC交于点O．连IJLMOI为所作截面．

评述本作法用到定理(4)、(5),其主要思路是:由P、Q找到点H,使点H与点R在同一面内(过点P、Q作点R所在面的垂线)．

思考在例4的作法中,若PE=QF,如何作图?

问题2.2 三点在长方体的相邻(不共点)的三个侧面上,如何作过此三点的截面?

例5长方体ABCD−A1B1C1D1,点R、P、Q分别为面AA1D1D、A1ABB1、B1BCC1上任意一点．作出过点R、P、Q的平面α截长方体ABCD−A1B1C1D1的截面．

图6

作法如图6,分别过点R、P、Q作平面A1B1C1D1的垂线,交棱A1D1、A1B1、B1C1于G、E、F,连EF、PQ交于点H,连PR、EG交于点S;连SH交A1D1、B1C1于J、I;连JR交A1A于K,连KP交B1B于L,连LI必过Q;连JKLIJ为所作截面．

评述关键是三侧面上的点向底面作垂线;平行线确定平面;找到一个面上的两点．

三、其它多面体的截面作图

有了以上的基础,其他问题就容易了．诸如:已知的三点中有些在长方体的面上(非棱)、有些在棱上的情况就可以解决．进一步可以处理其它多面体(一般棱柱＼棱锥、棱台等)的截面问题．

例6已知三点P、Q、R分别在四棱锥O−ABCD的三条侧棱OA、OB、OD上,求作过点P、Q、R的截面(假设PQ、PR都不与底面平行)．

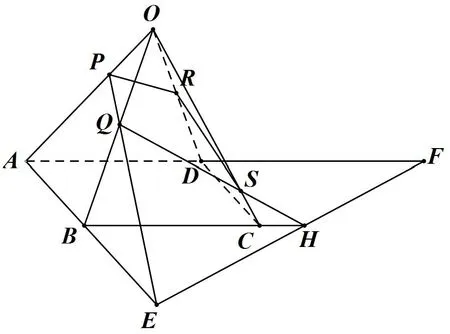
图7

作法

① 连PQ与AB交于点E,连PR交AD于点F;

② 连EF交BC于H,连QH与OC交于S;

③ 连RS,则四边形PQSR为所作截面．

(说明:若H在线段BC内,则截面为五边形.)

立体几何作截面是要求比较高且比较困难问题,本文主要以长方体为载体分析探究过已知三点做截面的思维方法,以期达到空间想象能力的再提高,奠定解决未来问题的基本思想方法．为了对以上问题类型与作图方法更全面的掌握,编写以下练习,加以巩固提高．

练习

1.长方体ABCD−A1B1C1D1,P、Q、R分别为B1C1、A1A、AB上任意一点.作出过点P、Q、R的平面α截长方体ABCD−A1B1C1D1的截面．

2.长方体ABCD−A1B1C1D1,P、Q、R分别为C1C、A1A、AB上任意一点.作出过点P、Q、R的平面α截长方体ABCD−A1B1C1D1的截面．

3.正三棱柱ABC−A1B1C1,P、Q、R分别为AA1、BB1、A1C1上任意一点.作出过点P、Q、R的平面α截正三棱柱ABC−A1B1C1的截面．

4.正四棱锥S−ABCD,P、Q、R分别为AD、BC、SC上任意一点．作出过点P、Q、R的平面α截正四棱锥S−ABCD的截面．

5.正三棱锥S−ABC,P、Q、R分别为SA、BC、SC上任意一点．作出过点P、Q、R的平面α截正三棱锥S−ABC的截面．