基于微课的学生说题案例探析
谢春华+陈海烽


[摘 要] 本文通过分析,界定学生说题的定义,接着展示一个学生利用微课说题的案例和学生制作微课的体会,从而提出可以开展让学生通过一道题制作微课的学生说题活动,提出学生制作微课,可以提高他们的学习效益,提高他们的思维能力,提高他们的自我效能的观点.
[关键词] 微课;学生说题;案例
所谓微课,一般是指时间小于15分钟的微视频讲解. 说题,就是将题目的解答思路、方法和解题过程展示出来,达到给予听众启发或共鸣的目的. 学生说题微课是指学生自己制作微视频,将自己对一道题的解答过程分析出来,展示给其他同学. 微课具有可重复使用的优越性,可以迅速在全国传播开来,但是让学生特别是初中生自己制作微课,展示自己对一道题的解题分析,案例尚不多见. 由于笔者承担了一个省级课题的缘故,笔者将之付诸实践.
正巧,笔者参加了一个区级的说题教研活动,说题的题目选自2016年福建三明市中考第25题,在说题过程中,笔者展示了笔者所在学校一位学生独立制作的微课,微课的内容就是解题过程,受到在场所有老师的称赞,都说“学生的能量不可估量”!在赞叹学生能力的同时,教师纷纷对我们的课题表现出了浓厚的兴趣. 现将该生的微课说题过程整理如下.
学生的微课说题过程
1. 题目呈现
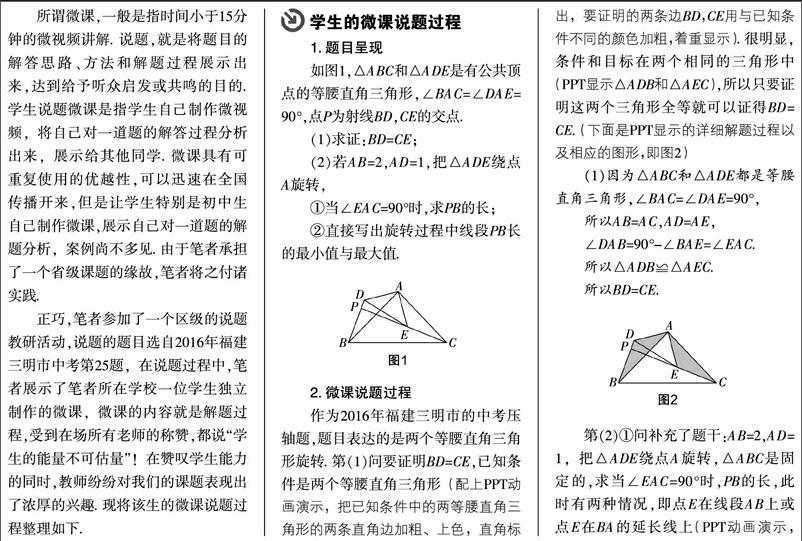
如图1,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最小值与最大值.
2. 微课说题过程
作为2016年福建三明市的中考压轴题,题目表达的是两个等腰直角三角形旋转. 第(1)问要证明BD=CE,已知条件是两个等腰直角三角形(配上PPT动画演示,把已知条件中的两等腰直角三角形的两条直角边加粗、上色,直角标出,要证明的两条边BD,CE用与已知条件不同的颜色加粗,着重显示). 很明显,条件和目标在两个相同的三角形中(PPT显示△ADB和△AEC),所以只要证明这两个三角形全等就可以证得BD=CE. (下面是PPT显示的详细解题过程以及相应的图形,即图2)
对于第二种情况,即点E在BA的延长线上时,方法与第一种情况相同(PPT展示具体的解题过程,重要结论打红色“√”,配图如图5),具体的解题过程如下:
第(2)②问是求在△ADE旋转的过程中BP的最大值和最小值. 因为B为定点,P为动点,所以要求BP的最大值与最小值,要清楚点P的运动规律. 注意到在△ADE旋转的过程中△ADB≌△AEC是确定的,所以∠DBA=∠ECA. 因为∠ABC+∠ACB=90°,所以∠PBC+∠PCB=90°. 所以∠BPC=90°. 所以点P在以BC为直径的圆上运动(PPT演示点P的运动轨迹,即以BC为直径的圆,配图如图6).
显然,当BP所对的圆周角越小时,BP越小;当BP所对的圆周角越大时,BP越大. 但是,对于这个圆周上的任何一点,点P都能到达吗?这要回到点P的定义中去看. 题干中给出点P为射线BD,CE的交点,那么射线BD,CE到不了的地方,点P就到不了. 在点B,D,C,E中,B,C两点为定点,D,E两点为动点. D,E在以A为圆心、1为半径的圆(⊙A)上运动(PPT动画显示以A为圆心,AD长为半径的圆,并用紫色凸显),所以CE与⊙A要有交点,点P才能存在. 要求CE与圆有交点,又要求∠BCP的最小值,所以BP取得最小值时,就是CE与⊙A在下面相切(图7)时;当取得最大值时,就是CE与⊙A相切在上面(图8)时(PPT演示CE与⊙A相切的两种情況). 思路理清了,解题过程就很简单了. 下面是详细的解题过程:
(2)②因为在△ADE旋转的过程中,
始终有△ADB≌△AEC,
所以∠DBA=∠ECA.
因为∠ABC+∠ACB=90°,
所以∠PBC+∠PCB=90°.
所以∠BPC=90°.
所以点P在以BC为直径的圆上运动.
因为AD=AE=1,所以在△ADE旋转的过程中,点D,E始终在以点A为圆心、1为半径的圆上运动(记作⊙A).
因为点P为射线BD,CE的交点,
所以当CE与⊙A相切时,BP取得最小值(图7)和最大值(图8).
总结 求几何动点最值问题的方法:(1)寻找动点的运动规律,有时动点在一次函数上运动,有时在圆上运动,有时在抛物线上运动. (2)寻找动点运动的范围,这要回到动点的定义中去求. (学生边说,边PPT演示总结过程,PPT如图9)
学生感悟
因为这个微课是我们课题组布置给学生的任务,我们只提供题目,其他PPT和微视频的录入都是学生自己一手完成,因此课题组对学生如何完成这个过程很感兴趣. 为此,笔者让学生写出其微课制作过程的心得体会.
感 悟
九年五班 陈姝妍
本次做的解题视频是2016年福建三明市最后一道题,这道题涉及等腰直角三角形的旋转. 这类题我们从初一做到初三,但每次遇到只有似曾相识的熟悉感,却没能一针见血地解答.
本来因为种种原因,这道题我没做,课堂上老师有讲解,我只把老师说的重点和答案抄了下来. 过了几天,老师让我做这道题的视频,我才把扔在柜子里的卷子找出来,花了几十分钟做了一遍,发现我原来连答案都抄错了. 这是我们普遍存在的问题,好题太多,难题做不完,老师却只有一个,嗷嗷待哺的学生近百个,加上时间不够,有时就要与部分数学题错过.
认真做这个视频的原因之一是我觉得这个视频有存在的意义,可以给很多和我一样的同学一些时间去理解这道题,再给我们一次听这道题解法的机会.
对我而言,决定要做视频了,要给同学讲题了,那我就会不自觉地转换角度看试题,不只是解决问题,而是解析试题. 这样一折腾,对于这道题甚至是这次做视频,我都有许多感触.
为了让更多的人听懂,自己首先要很懂很懂,所以我把题目重新看了好几遍,看到第三遍,才发现简单的第(1)问有更简单的解法,之前我做了一条辅助线,现在发现只要运用全等三角形,一步就可以完成. 既然是简单题,就要用最优方法迅速解决,给后面的难题、好题留足时间.
在第(2)②问中,题目只要求写答案不用写过程,我原来隐约感觉可能和圆有关,求最值最可能的就是相切的时候,算是半蒙半猜写出来的. 但是既然是讲给别人听,这样模模糊糊的观念不容易表达,也不准确,所以我研究了一会儿,发现这个模型中还隐藏着另外一个圆,之前老师没有特别强调,所以我当时听了就省略了,但其实这是问题的关键. 之后,我将两个圆结合起来,通过严谨的推理,说明了为什么相切时BP取到最值.
也许此时我依然没有领悟到动点问题的精髓所在,但开始录视频的时候,我尝试着用通俗的语言来表达出抽象的规律. 语言最奇妙的地方就在于,当你说出你的想法时,脑海中的想法会受到表达方式的微妙影响. 然后我灵光一现,发现动点是动的,但规律却是固定的!其他题目,哪怕不是在圆上运动,在抛物线或在直线上运动,只要发现规律,找到对应的定义域,再略加分析,就能解决所有此类型的动点最值问题——这一总结才是我最大的收获.
不管这个视频对别人而言如何,于我就是一次沉下心思考、总结的过程,我竟意外地在路上捡到许多洒在脚下的珠宝,收获满满.
教学启示
1. 学生微课说题可以提高他们的学习效益
学习金字塔(图10)最早是由美国学者、著名的学习专家爱德加·戴尔1946年发现并提出的,主要是考查学生两周后对于知识还能记住多少. 从中我们发现,塔顶就是我们最常见的第一种学习方式——听讲,学习保持率为5%. 而塔底是最佳的学习方式,就是“教别人”或者“马上应用”,可以记住90%的学习内容. 学生微课说题,就是让学生进行信息输出,他们首先要完成对本试题的理解,在此基础上才有可能输出. 从学生做微课的感受我们可以发现,学生本来只抄写了解题重点和答案,后来却花了几十分钟去解析试题,从解析试题中我们可以发现学生终于理解并达到通透的层次. “然后我灵光一现,发现动点是动的,但规律却是固定的!”从中可以看出一个学生凤凰涅槃、破茧成蝶的过程. 这个过程让学生所获数学解题经验比原来做许多类似的题还要多.
2. 学生微课说题可以提高他们的思维能力
学生在解析试题的过程中,通过审题,给试题的条件进行标注,可以发现有两个全等三角形. 这其实就是我们经常告訴学生的“要怎么做”. 这里学生自己已经体会到如何做,而且通过学生来告诉学生,显然更具可信度. 换句话说,就是更接地气. 从学生研题的过程可以看出,学生开始感到本题和圆有关,但这只是她的直觉,后来通过研究最终证实了这一想法的正确性,而且还在此过程中发现了老师在课堂上没有讲的东西. 由此不难看出学生的逻辑推理素养. 最妙的是,学生对动点最值问题规律的发现,这也是本题的奥妙所在,这个规律是今后解决一大类动点问题的基础. 有个这个思维上的突破,等于提高了自己的数学素养,即数学抽象能力.
3. 学生微课说题可以提高他们的自我效能
学生通过自己呈现微课,做自己同学的老师,能留住自己的东西,同时感受到自己存在的价值. 同学也会对自己有更严格的要求,正如学生所说:“我尝试着用通俗的语言来表达出抽象的规律. 语言最奇妙的地方就在于,当你说出你的想法时,脑海中的想法会受到表达方式的微妙影响. ”同时学生还阐述了自己对找到规律时表现出的兴奋,即发现了解决动点最值问题的一般方法,这是学生送给自己最好的礼物. 我们有理由相信,通过微课说题,学生会更加自信地出现在考场,对动点最值问题不再犯愁.
通过课题组成员的共同努力,我们对学生微课说题的生命力充满了信心. 现在很多学生已加入微课说题制作的大军,学生由被动听题到自己主动说题,由原来的无序思维和混沌状态到逻辑有序,随着学生微课说题案例的丰富,我们强烈地感受到了学生的成长. 教学相长,这也促使教师在提供试题给学生时要更加重视试题的代表性,使学生成为某道题甚至某类题的专家.

