TK-MEDLL算法的GNSS实测数据多径分析
杨 茜,秦红磊,袁赫良
(北京航空航天大学 电子信息工程学院,北京 100191)
TK-MEDLL算法的GNSS实测数据多径分析
杨 茜,秦红磊,袁赫良
(北京航空航天大学 电子信息工程学院,北京 100191)
针对基带抗多径算法应用中MEDLL算法计算复杂度高、估计准确度不高和实测数据的多径分析没有标定参数的问题,提出分别采用TK-MEDLL算法和系统的实测数据多径分析方法:TK-MEDLL算法能在抗多径算法实际应用中减小计算复杂度以及提高估计精度;实测数据多径分析方法从实测环境、数据的相关域、伪距和定位等几个方面进行分析,对比得出实测数据可见星的多径情况。实验结果证明了提出方法的可行性和准确性,并能够应用于复杂环境中。
全球卫星导航系统;多径;参量式多径估计;TK-MEDLL
0 引言
卫星发射出电磁波信号后,一部分经直线传播直接到达地面接收机,另一部分可能经过接收机周围介质和障碍物的反射或折射后间接到达接收机,接收机同时收到这2种电磁波信号(如图1所示)的现象就叫做多径现象[1]87-89。在复杂环境尤其是高楼林立的城市里,全球卫星导航系统(global navigation satellite system,GNSS)接收机容易接收到一条或者多条的多径信号。
如果接收到的GNSS信号包括多径信号,那么接收机内部复制的伪随机码会同时与直射波和各个反射波做相关运算,使原本只反映直射波码相位情况的三角形自相关函数主峰遭到变形、破坏(如图2所示)[1]87-89,从而降低码相位的测量精度,严重时还可导致码相位失锁和卫星信号失踪。多径对载波相位的准确测量也有一定程度的干扰。
随着GNSS的应用越来越广泛,用户对卫星导航系统的定位精度也提出了更高的要求。影响定位精度的误差源包括卫星钟差、电离层延迟、对流层延迟、轨道误差和多径干扰等[2-3]。采用差分定位和模型改正,可基本消除卫星钟差、轨道误差、电离层和对流层延迟等[4]。而多径误差的无空间相关性和其时变性,导致多径信号不能通过差分或模型修正,且多径造成的定位误差可以达到m级;因此多径成为复杂环境中高精度用户的最主要误差源。多径的抑制和消除技术尤为重要。
多径抑制技术大致可分为3大类:一是天线端抑制多径技术;二是基带信号处理技术;三是测量域处理技术。
天线端多径抑制技术主要有扼流圈天线[1]333-341和天线阵列[4]。前者是抑制小仰角信号的进入;后者是通过直射波和反射波在空域上具有不同特征的性质区分直射和多径,然后调整天线阵列各阵元的加权值,使得整个阵列在直达信号方向上的响应等于1,多径方向上的响应等于0,保证直达信号无失真地被接收的同时,抑制多径信号。
基带信号处理阶段的多径抑制又可以分为非参量式和参量式2种处理方式。非参量式多径抑制方法通过改变鉴相曲线形状来降低多径对伪距测量的影响,例如窄相关技术[5]、早晚码斜率(early late slope,ELS)技术[6]、Strobe技术[7]等。这一类算法复杂度低,实现较为简单。参量方法的主要思想是对直达信号和多径信号的条数、幅度、延迟、相位进行估计,从而分离直达信号和多径信号。多径估计延迟锁定环(multipath estimating delay lock loop,MEDLL)[8]是经典的参量式估计,与非参量方法相比,这类方法计算复杂度相对较高;但能较为准确地估计出多径参数。
测量域的抗多径算法研究,主要集中在2个领域:载波相位平滑伪距算法和多频码多径组合。前者是利用测量精度更高、多径误差更小的载波相位测量值来对多径误差更大的码伪距观测值进行平滑修正。后者则是利用多频信号的码与载波相位观测量的线性组合,提取出码伪距值中的多径误差部分。测量域的数据后处理方法需要长时间观测;因此更适合于监测站等位置固定,并能够进行长时间观测的应用场景。
本文研究的是参量式基带抗多径方法,MEDLL算法是经典的参量式估计,它能有效地减小多径效应给码相位和载波相位的测量值带来的误差,消除窄相关接收机中90 %的多径效应,在性能上接近没有多径情况下的全球定位系统(global positioning system,GPS)测量精度理论值。1997年,NovAtel公司在接收机上实现了此算法,虽然计算量大,难以完成实时检测;但其估计多径参数的性能是其他算法无法比拟的[8]。Teager-Kaiser(TK)算子[9]是一个非线性算子,能够跟踪信号的瞬时能量。在近期的研究中,TK算子一般与参数估计类算法相结合,能够有效地估计短延时多径效应。TK的计算负担很低,并且可以用在较少相关器的情况下。TK与MEDLL的结合可以改进MEDLL算法计算量大的不足,且能提高多径参数的估计精度。
本文旨在研究并实现TK-MEDLL算法,最后通过实验验证算法的有效性。
2 多径信号模型
天线接收到的卫星导航信号的直射波
rd(t)=Ap(t)sin (2πft)。
(1)
式中:A为信号的振幅;p(t)为数据码和伪码的异或和,取值为+1或者-1;f为载波频率,需考虑多普勒效应。
此直射信号的第i个反射波
ri(t)=αiAp(t-τi)sin (2πf(t-τi)+Δφi)。
(2)
式中:αi是反射波的幅度衰减系数;τi是第i路反射波相对于直射波的传播延时;Δφi是各个反射面造成的信号相位变化和。因此,第i路反射的多径相对于卫星直达信号的总相位变化
φi=Δφi-2πftφi。
(3)
接收机实际接收到的信号是直射波和多个可能的反射波的叠加,即
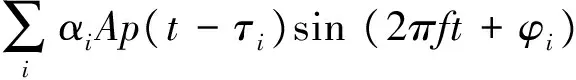
(4)
每路反射波都可用其相对于直射波的载波相位变化φi、传播时延τi和幅度衰减系数αi等3个参量来进行完整描述。
多径效应发生时,接收天线接收到的是这颗卫星发射信号的直射波和反射波相叠加的信号,于是接收机随后处理的接收信号也是这些直射波和反射波的叠加,它一般不能将直射波和混杂在一起的各个反射波区分开来。这样,当接收机的一个信号通道将接收信号与其跟踪环路所复制的伪随机码进行相关运算时,实际上复制的伪随机码分别同时与反射波和直射波进行相关,最终的相关结果是这些相关值的叠加。相关积分后的自相关函数可以表示为
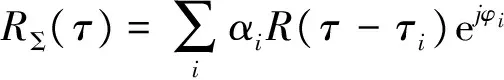
(5)
式中:R(τ)表示伪随机码的自相关函数;幅度衰减系数αi实际上还包含着反射波直射波的相干积分误差损耗。
2 TK-MEDLL算法
2.1 算法简介
MEDLL信号估计,多径信号的数目未知,首先估计离直达信号最近的一条多径信号和它的参数,循环更新直射和多径信号;然后加入第二条多径信号,并估计参数,循环更新信号; 以此往复,直到合成信号均方误差最小。这个过程的计算很复杂,同时运算量大。
将TK 算子应用到卫星导航的多径估计[10]中,计算相关函数的TK算子En=R(n+1)·R(n-1)-R2(n),其中R(n)表示相关函数,n表示相关器序号。通过检测门限值的设置,可以迅速且准确地估计出多径数目M,而且可以给出估计幅度、延时和相位的初值,使估计值能够更快收敛。针对 MEDLL 中的不足,以及 TK 算法的简单性,可以将 TK 算子和 MEDLL 结合起来,从整体上来估计多径信号,减小其运算量[11]。
TK-MEDLL的基本流程如图3所示。
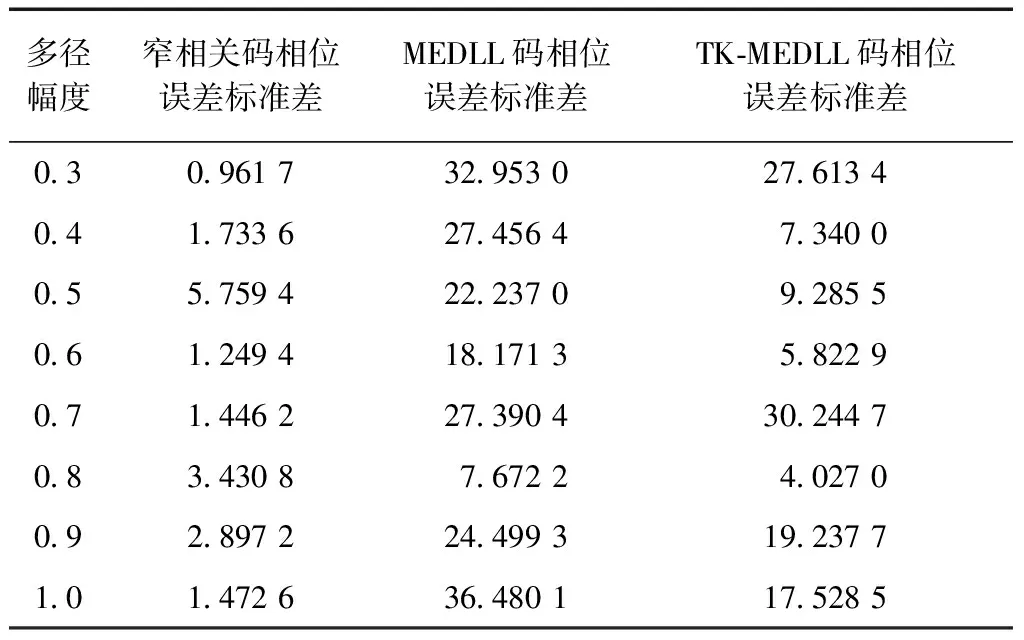
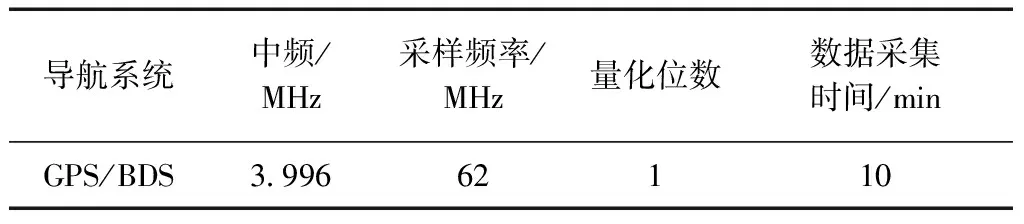
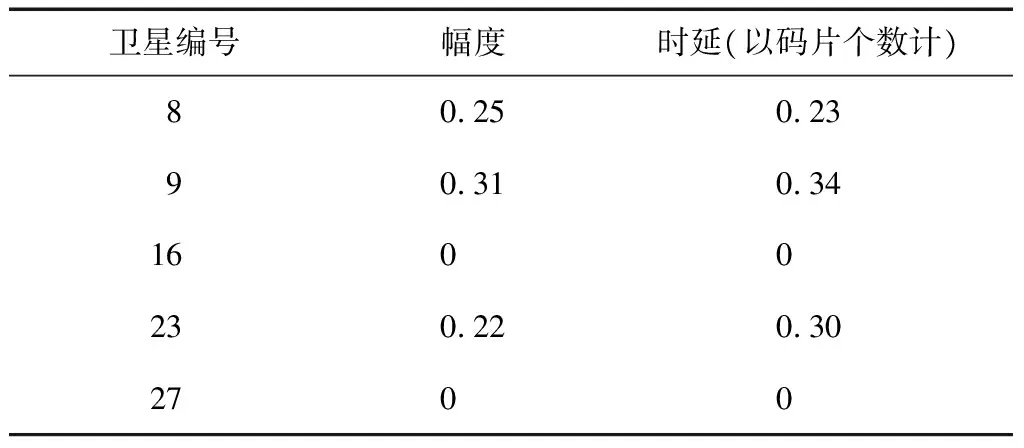
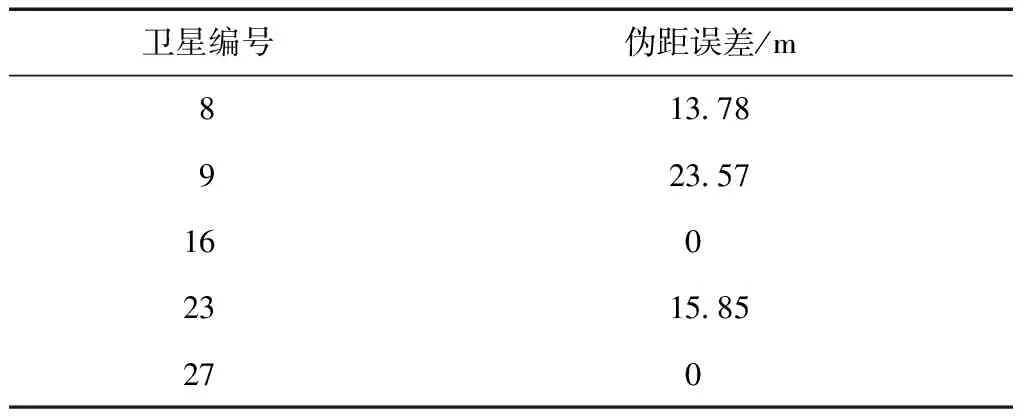
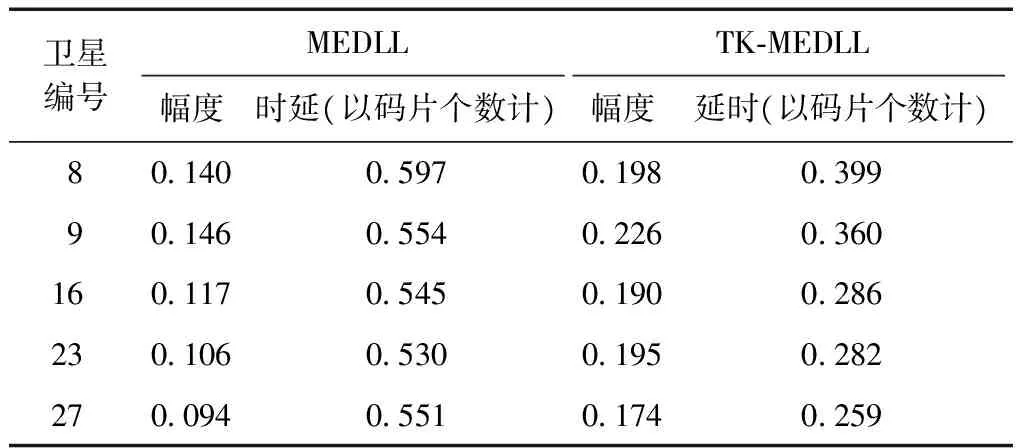
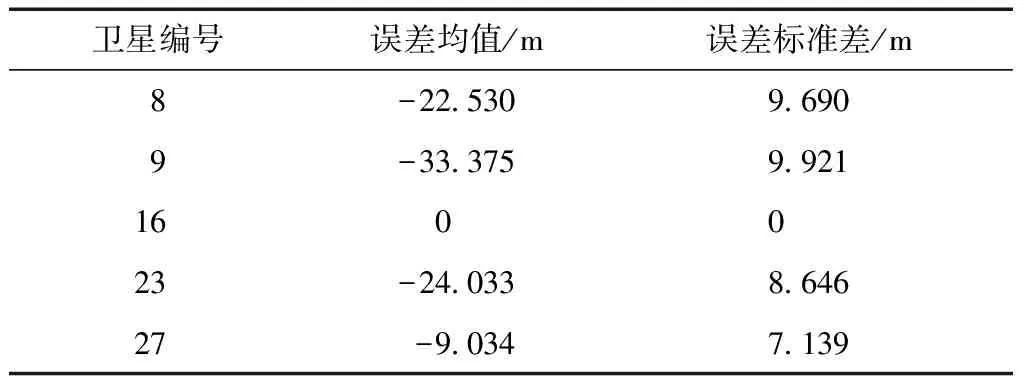
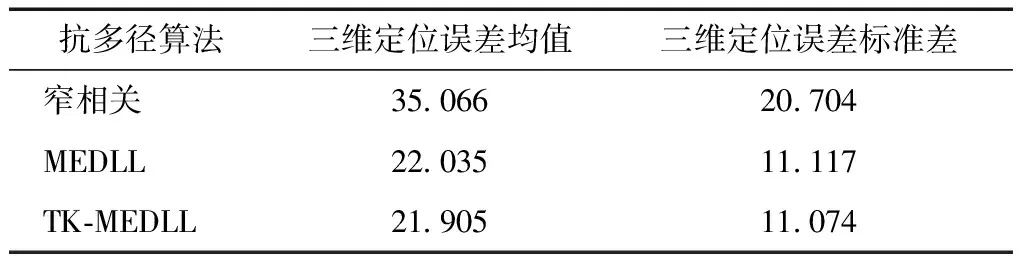
在TK-MEDLL算法中存在2个判断条件:一个是根据TK算子判断估计多径数目,即TKThresh=max(TK)WTK+NThresh,式中TKThresh为TK算法门限值,max(TK)为TK算子的最大值,其中还有2个门限,即噪声门限NThresh和检测门限WTK;另外一个是判断算法循环到收敛的条件Res(p)-Res(p-1) WTK为检测门限,通过将TK算子运用到理想相关函数上仿真而得,一般取值[12]为: 0.25≤WTK≤0.3, 对于BPSK; 0.3≤WTK≤0.32, 对于sin BOC。 其中BPSK为二进制相移键控调制(binary phase shift keying),BOC为二进制偏移载波调制(binary offset carrier)。 NThresh为噪声门限,是有噪声相关函数除主瓣之外相关函数的平均值,即取以峰值为中心的矩形窗口以外的相关函数的平均值。窗口宽度一般不小于2个码片,通常NThresh为0[12]。 EOL为残余能量门限,通过仿真可得到,取EOL=10时残余能量收敛,算法性能良好。 2.2 改进优点 TK-MEDLL的改进主要是2个方面,第一是估计精度的改善,第二是计算复杂度的改善。估计精度的衡量从2个方面开展:首先是从相关域出发的多径估计值的误差衡量;其次是码相位误差衡量。这部分的试验是通过模拟数据测试,模拟数据包括2颗卫星,一颗实验卫星有直射信号和多径信号,另外一颗是标定卫星只有直射信号,2颗卫星设置相同参数,以相同的初始码相位发射信号。下文中多径时延是指多径信号对于直射信号的时延(单位为码片个数),多径幅度是指多径信号对于直射信号幅度之比。 利用MEDLL算法和TK-MEDLL算法对试验卫星数据进行多径估计,与设定多径参数进行比较得到多径估计值误差,可以得到不同多径幅度的估计值误差均值,其结果见图4~图5。 对试验卫星信号进行多径估计,然后构造直射信号返回给接收机,计算其码相位并与标定卫星的码相位进行对比,得到不同多径幅度下的码相位误差和标准差,其结果见表1~表2。 从多径估计值和码相位的分析中可以看到:1)TK-MEDLL估计多径幅度和多径延时误差均小于MEDLL,且TK-MEDLL幅度误差小于0.03,延时误差均值小于0.05;2)TK-MEDLL相对于MEDLL的码相位误差改善在55 %以上。所以TK算子与MEDLL的结合提高了估计精度。 表1 不同多径幅度的码相位误差均值 m 表2 不同多径幅度的码相位误差标准差 m 同时可以看出MEDLL系列算法相对于窄相关算法的码相位误差均值更大,误差标准差更小。由于MEDLL系列算法用到更多的相关器,有较多的信息,码相位误差的估计更为准确,所以其码相位误差均值相对更小;同时MEDLL系列算法作为参量式估计,其进行多径参数的估计时受到噪声的影响相对较大,所以其码相位误差标准差相对于窄相关算法较大。 若M为多径数目,NIter为设置的最大迭代次数,N为相关函数的采样点数,以最大似然对一路信号的估计为一次计算,MEDLL算法的估计次数是(1+2+…+M)·NIter,而TK-MEDLL算法的估计次数是M·NIter。估计算法的复杂度与相关函数的采样点数成正比,所以TK-MEDLL算法将算法复杂度从O(M2NIterN)减小到O(MNIterN)。 综上,TK-MEDLL算法从估计精度和算法复杂度2个方面都做出了改进。 本节是基于TK-MEDLL 算法对实测数据的分析,同时提出一套较为完整的实测数据多径分析方法。 实测数据采集于2016-03-25北京航空航天大学新主楼二楼的平台中心(经纬高:39.978 86°N,116.345 618°E,49.97 m,如图6所示),正好处于连体教学楼的包围之中,具有天然的多径环境。 采集时通过2路同时采集:一路是中频卫星导航数据采集,通过天线、下变频、模/数转换器(analog-to-digital converter,ADC)采集到计算机存储数据;另外一路是超高速采集设备直接采集射频信号,不仅能够排除下变频可能引入的干扰,而且可以获得高分辨率的相关域结果。采集现场和原理示意如图7和图8所示。 中频数据采集的基本参数如表3所示。 表3 中频实测数据采集参数 超高速射频数据采集的基本参数如表4所示。 表4 超高频实测数据采集参数 实测数据的分析方法如下:首先根据采集数据场景和卫星星历建模分析其多径情况;接着根据卫星导航接收机处理信号流程相关域、伪距域及定位参数等,对应进行估值、伪距误差和定位误差的分析;同时对高分辨率的相关域结果进行SCB偏差分析;最后是对比分析实测数据的可见星多径情况。实测数据分析方法的原理如图9所示。 3.1 多径建模分析 多径建模是首先根据实测数据的场景进行测量环境建模,然后根据精密星历计算卫星位置,最后通过卫星与天线的相对位置判断实测场景中可能存在的反射。对上述实测数据的场景时间等建模,可以得到多径参数,其结果见表5。 表5 实测数据建模多径参数 同时可以根据多径参数计算出多径(1条多径)对伪距的影响[13]为 (6) 表6 实测数据建模伪距误差 3.2 估计值分析 估计值分析是指基于最大似然估计的2种参量式估计MEDLL算法和TK-MEDLL算法对数据的分析。对导航数据进行20 ms的积分相关,TK-MEDLL和MEDLL对此相关函数进行估计,统计10 min的估计值。统计结果如表7所示。 表7 2种算法下的多径估计值 MEDLL和TK-MEDLL 2种算法估计的多径参数并不相符。同时将MEDLL、TK-MEDLL的估计结果和多径建模估计参数进行对比,多径参数数值上没有匹配,但是从2种方法的多径幅度可以看出:#9多径幅度>#8多径幅度>#23多径幅度>#16多径幅度≥#9多径幅度;即:#8、#9、#23卫星多径幅度较大,#16、#27卫星多径幅度较小。 3.3 SCB偏差分析 SCB偏差表示相关曲线左右两侧对称点与最高峰值的偏差。由于接收机是通过码跟踪环路的相关曲线获得码鉴别器结果与零数偏差的,因此需要进一步调整跟踪环[14]。SCB偏差采用不同相关间隔获得对应的早码-晚码的鉴别器结果,分析相关峰偏离中心零点的位置。其相关间隔d、码相位误差ε与鉴别器结果的定义[12]为 (7) 式中:SC代表S曲线;CCF代表r(t)经过载波剥离和与本地伪码相关后的信号;RE代表信号与早码的相关值;RL代表信号与晚码的相关值。锁定点的位置εbias(d)的定义为 SC(εbias(d),d)=0。 (8) 假设只存在一路多径信号(i=1),根据式(7)及式(8)可得出锁定点位置 (9) (10) A=2Y/X; (11) 根据式(11),可以在得到实际信号的SCB偏差后,根据拐点信息求出多径的参数估计值。 以实测数据的#27卫星为例,计算其实测SCB曲线,接着拟合到仿真曲线,根据仿真曲线的拐点计算其多径参数(幅度0.109,延时0.111),其结果见图10。 以上述的SCB 偏差分析方法计算其他4颗星的多径参数,如表8所示。 表8 SCB 偏差分析 SCB偏差分析的多径参数与多径建模结果,虽然数值不匹配;但是从幅度大小可以看出,在2种方法下都是#8、#9卫星多径幅度明显大于其他卫星, #16、#27卫星多径幅度较小。与之前的估计值分析的结论相似,只是在#23卫星的幅度大小有差异。 3.4 伪距误差分析 伪距误差分析是从接收机处理过程中的伪距角度进行分析。首先可知伪距测量噪声量ερ=r+δtu-ρc,主要部分为多径误差和热噪声,所以可以用来衡量多径伪距误差[1]69-72。其中修正伪距ρc、接收机钟差δtu是软件接收机处理数据过程中得到的参数;r是计算天线和卫星之间的准确距离。卫星位置是下载精密星历得到的,精密星历位置精度5 cm。计算可知,5颗卫星的伪距测量噪声量均存在周期性的波动(以#8卫星为例),此波动是残余的接收机钟差,是公共误差。#8卫星的伪距噪声量如图11所示。 由于#16卫星仰角64°,存在多径的可能性小,所以将#16伪距测量噪声量作为基准,计算其他4颗卫星的伪距误差(以#8卫星为例),并统计各颗卫星的伪距误差。#8卫星的伪距误差如图12所示。5颗卫星的伪距误差统计结果如表9所示。 卫星编号误差均值/m误差标准差/m8-2253096909-333759921160023-24033864627-90347139 此部分的伪距误差与多径建模得到的伪距误差对比,2组伪距误差公共误差为9 m左右。去掉公共误差之后,可以得到#8、#9、#23卫星伪距误差大,#16、#27伪距误差小。通过上述3个分析方法,可以得出结论:#8、#9、#23可能存在多径,#16、#27可能不存在多径。 3.5 定位精度分析 最后是定位精度的分析,计算数据定位结果与标定位置(即纬度39.978 886°N,经度116.345 618°E,高度49.97 m)之差。 通过上述几条分析,可知#8、#9、#23号卫星存在较大幅度的多径,对其使用MEDLL算法或者TK-MEDLL算法,并且将估计的直射相关值返回到软件接收机,得到新的定位结果。将10 min的定位结果进行误差处理并统计,结果见表10。 表10 2楼三维定位误差统计 m 可以看出:MEDLL和TK-MEDLL算法相对于窄相关定位误差提高13 m以上,标准差提高9 m;TK-MEDLL相对于MEDLL定位误差提高1 m,标准差改进较小。 本组实测数据的多径分析,通过多径建模、估计值、伪距误差和SCB偏差分析得出: #8、#9、#23卫星可能存在多径;#16、#27不存在多径。在多径存在可能性高的卫星加入参量式估计,并将直射结果返回到后续的接收机处理中,TK-MEDLL相对于窄相关算法的定位精度提高14 m。同时也验证了提出的实测数据分析方法的可行性和正确性。 本文首先研究了参量式多径估计算法,结合TK算子的简单性和MEDLL算法的准确性,得到新的算法TK-MEDLL,既提高了估计的精度,又减小了算法的复杂度。并且通过模拟数据测试了TK-MEDLL算法相对于MEDLL算法的改进优势。 基于参量式多径估计算法的研究,本文提出一套实测数据的多径分析方法。首先根据实测环境进行多径建模,接着从相关域、伪距、定位3个方面分别进行相应的多径分析,最后以北航新主楼采集数据为实验数据,分析了5颗可见星的多径情况,验证了本套分析方法的可行性。 [1] 谢钢. GPS 原理与接收机设计[M]. 北京:电子工业出版社, 2009. [2] 金育兵, 蒋谢彬. GPS系统多径干扰分析及消除技术[J].无线电通信技术, 2001, 27(3):33-34. [3] 张孟阳,吕保雄,宋文森,GPS系统中的多径效应分析[J].电子学报,1998,26(3):10-14. [4] JOHAN M. Robust navigation with GPS/INS and adaptive beamforming[J]. Scientific Report of Swedish Defence Research Agency, 2003: 1650-1942. [5] DIERENDONCK A J, FENTON P, FORD T. Theory and performance of narrow correlator spacing in a GPS receiver[J]. Navigation, 1992, 39(3): 265-283. [6] IRSIGLER M, EISSFELLER B. Comparison of multipath mitigation techniques with consideration of future signal structures[C]//The Institute of Navigation. Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation(ION GPS/GNSS 2003). Portland, Oregon: The Institute of Navigation, Inc., 2003: 2584-2592. [7] GARIN L, ROUSSEAU J M. Enhanced strobe correlator multipath rejection for code & carrier[C]//The Institute of Navigation. Proceedings of the 10th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1997). Kansas City, Missouri: The Institute of Navigation, Inc., 1997: 559-568. [8] NEE R. The multipath estimating delay lock loop: approaching theoretical accuracy limits[C]//The Institute of Electrical and Electronics Engineers(IEEE). Proceedings of the IEEE:Position Location and Navigation Symposium (PLANS). Las Vegas, Nevada: IEEE, 1994: 246-251. [9] HAMILA R, LOHAN E S, RENFORS M. Subchip multipath delay estimation for downlink WCDMA system based on Teager-Kaiser operator[J]. IEEE communications Letters, 2003, 7(1): 1-3. [10]HAMILA R, RENFORS M. Nonlinear operator for multipath channel estimation in GPS receivers[C]//The Institute of Electrical and Electronics Engineers(IEEE). Proceedings of the 7th IEEE International Conference on Electronics, Circuits and Systems. Jounieh, Lebanon: IEEE, 2000: 352-356. [11]魏国庆,黄勇,刘立汉,等.一种GPS多径抑制的改进方法[J].西华大学学报(自然科学版),2011,30(1):35-37. [12]BHUIYAN M Z H, LOHAN E S, RENFORS M. Code tracking algorithms for mitigating multipath effects in fading channels for satellite-based positioning[J]. EURASIP Journal on Advances in Signal Processing, 2007, 2008(1): 1-17. [13]RAY J K. Mitigation of GPS code and carrier phase multi-path effects using a multi-antenna system[EB/OL].[2016-05-30].http://www.ucalgary.ca/engo_webdocs/MEC/00.20136.JayantaRay.pdf. [14]张孟阳,吕保维,宋文淼.GPS系统中的多径效应分析[J].电子学报,1998,26(3):10-14. Multipath analysis of GNSS measured data based on TK-MEDLL YANGQian,QINHonglei,YUANHeliang (School of Electronic and Information Engineering, Beihang University, Beijing 100191, China) Aiming at the problem that there is high computational complexity, low estimated precision and no calibrated parameter in the multipath analysis of measured data for MEDLL algorithm applicated in baseband anti-multipath algorithm, the paper proposed to adopt the TK-MEDLL and the systematic multipath analysis method of measured data: TK-MEDLL simplified the computation and improve the estimated accuracy in the application of the anti-multipath algorithm; meanwhile, the multipath analysis method comparatively induced the multipath parameters of visible satellites with measured data from the aspects of real environment, correlation domain, pseudorange and positioning.Experimental result proved the feasibility and accuracy for the application in complex environment. GNSS; multipath; multipath parameter estimation; TK-MEDLL 2016-08-24 杨茜(1992—),女,陕西咸阳人,硕士研究生,研究方向为卫星导航抗多径算法。 杨茜,秦红磊,袁赫良.TK-MEDLL算法的GNSS实测数据多径分析[J].导航定位学报,2017,5(2):117-124.(YANGQian,QINHonglei,YUANHeliang.MultipathanalysisofGNSSmeasureddatabasedonTK-MEDLL[J].JournalofNavigationandPositioning,2017,5(2):117-124.)DOI:10.16547/j.cnki.10-1096.20170221. P A 2095-4999(2017)02-0117-08
3 实验与结果分析

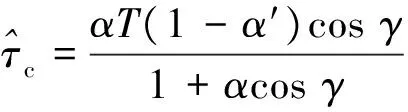
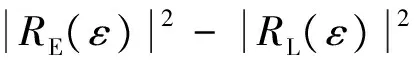
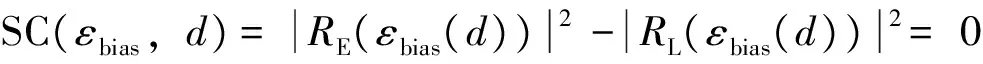
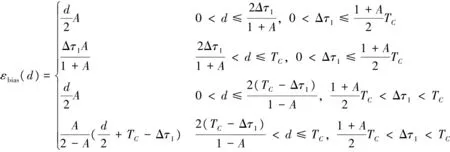
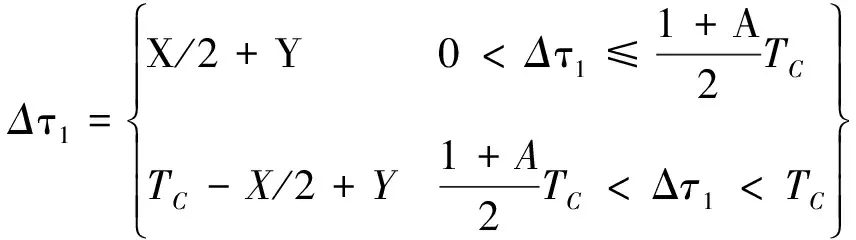

4 结束语

