基于数学建模思想的高等代数课程教学研究

李 丽, 杨方白, 门桐宇, 唐佳玥

(1. 沈阳师范大学 数学与系统科学学院, 沈阳 110034; 2. 辽宁师范大学 数学学院, 辽宁 大连,116029)



基于数学建模思想的高等代数课程教学研究

李 丽1, 杨方白2, 门桐宇1, 唐佳玥1

(1. 沈阳师范大学 数学与系统科学学院, 沈阳 110034; 2. 辽宁师范大学 数学学院, 辽宁 大连,116029)

探讨如何在高等代数中融入数学建模思想,通过增强其应用性,帮助学生更深刻的理解高等代数内容,使其认识到学习高等代数的重要性和必要性。但是,由于高等代数教学中所涉及的例子很少能与实际生活相联系,学生感到学习内容抽象,感受不到数学的应用价值,缺少学习的兴趣和动力。通过在教学中融入数学建模思想,对试验数据进行分析建模求解,将知识由抽象转化为直观形象的生活实例,由理论转化为应用,来增强学生学习高等代数的兴趣,提高教学质量及学生的数学素质,从而培养学生的创新思维意识及数学应用意识。

数学建模; 高等代数; 教学; 数学应用

当今社会,数学知识被广泛应用到各个领域并起着至关重要的作用。《高等代数》作为大学数学学习中的一门传统学科,其内容结构清晰,是大学数学的主干基础课程。但是,由于它的抽象性较强,并且学习内容较多,导致很难将所讲内容与实际相结合,所以教师的上课内容局限在概念教学。这种教学方法往往忽略了高代的实用性,而且学生体会不到学习高代的实际意义所在。因此,在《高等代数》课程教学中突出其应用性[1-3]已经成为该课程教学改革的热点。

随着数学建模竞赛的深入开展,为新的教学模式打开了新思路[4]。数学建模思想能够使数学知识形象化,系统化和实用化,是将数学与实际联系起来的纽带。因此,将数学建模思想融入高等代数课程教学中成为了高等代数课程改革的核心与重点。实践教学中表明,将数学建模思想融入到高等代数中有利于提高学生学习效果,使其体会到将数学应用到实际问题中去的魅力,激发学生的兴趣,提高学生学习的积极性,还能促使教师提高自身的专业素养,从而培养全面发展的创新型高素质人才。这样的教学方法既能弥补教材中理论联系实际不足的现象,又能帮助学生更深刻地理解课程的内容,培养学生创新能力。

1 在高等代数教学中融入数学建模思想的教学探索

1.1 在高等代数教材中充实应用素材

目前,大多数高校选择的高等代数教材在内容的取舍和体系结构上都比较得当,且具有理论性强,方法多样,重技巧性的特点。但是由于含有较多知识点,教师往往会采用理论教学模式,这导致部分学生对这门课程的学习热情不高。所以,高等代数教材的改革中应该具有以下特点(探讨了在不同模块中从背景知识、应用案例、信息技术、知识覆盖面、知识体系等角度入手将数学建模思想渗透于高等数学教材中)[5]:1)应充实一些趣味性的实例,例如:人口迁移模型,投入产出模型等。2)可以使用目前已经很成熟的计算机软件,如MATLAB,Lingo等,结合应用型实例,进行图示,数值计算,仿真等,以提高课堂教学的效果[4]。

1.2 在高等代数课程教学中教学方法的改革

1.2.1 在概念教学中引入数学建模的思想

在高等代数的学习中,概念是基础,只有深刻理解概念,才能应用到习题中去。为了让学生更好的理解概念,教师可以向学生传授概念的形成过程及应用,尽可能在实际问题中找到概念的原型。通过在实际问题中建立数学模型,来引出数学概念,这样可以加深学生对所学知识的理解与掌握,引发学生学习的欲望,使其主动去求知、探索与实践。

例1 行列式概念的引入[6]

货物交换的经济模型:诺贝尔经济学奖获得者列昂杰夫(Leontief)考虑的一个经济学模型。在一个原始部落,根据分工,人们分别从事3种劳动:农田耕作(记为F)、农具与工具的制作(记为M),以及织物的编织(记为C),人们之间的贸易是实物交易。图1给出这3人之间的交易系统,图中所示表明,农夫们将每年收获的一半留给自己,并分别拿出1/4给工匠们和织布者们;而工匠们却平均分配他们制作的用具给每个组;织布者们则留下1/4的衣物给自己,并拿出1/4 给工匠们、1/2给农夫们。此交易系统也可以用表给出,如表1所示。

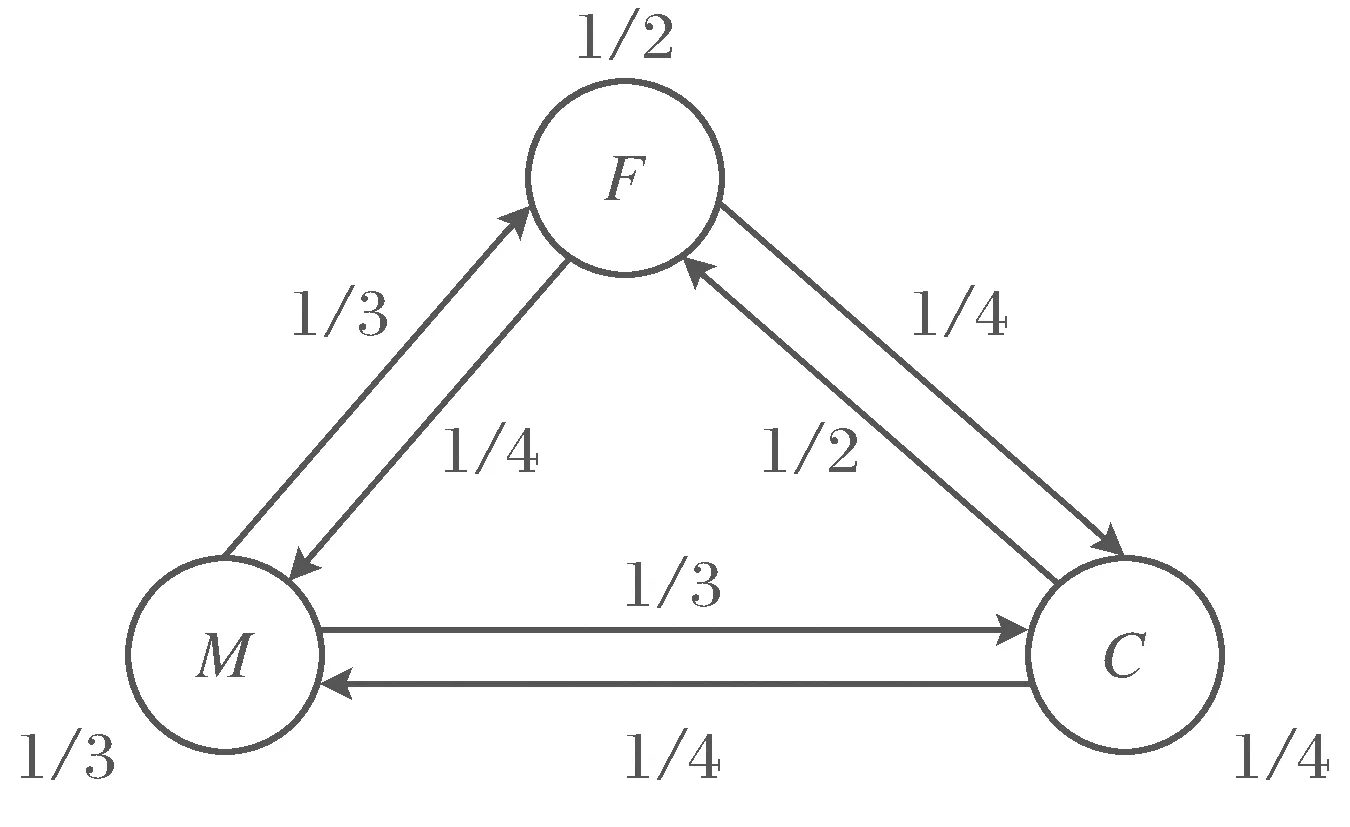
图1 三组人之间的交易系统

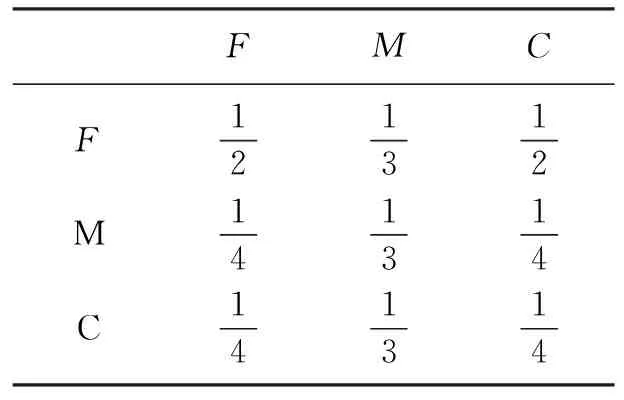
FMCF121312M141314C141314

随着社会的发展,实物交易形式变得十分不方便,于是部落决定用货币进行交易。假设没有资本和负债,那么如何给每类产品定价,使其公正地体现旧有的实物交易系统呢?

令x1为农作物的价值,x2为农具及工具的价值,x3为织物的价值,那么由表1,农夫们生产的价值应等于他们交换到的产品(包括留给自己的)价值,

(1)

即有

整理得,如下方程组:

(4)

因此,该问题可归结为一个三元一次线性方程组的求解问题。以此问题引出行列式,使学生了解行列式与线性方程组的密切联系。从简单的经济问题入手,让学生了解知识的应用背景,表明学习行列式是为生产实践服务的,从而提高学生学习的积极性。

1.2.2 在例题讲解中引入数学建模的思想

高等代数课程抽象,理论性强,且教材中缺少实用性例子,导致大多学生认为高等代数与实际无联系,从而丧失学习的兴趣[7]。为了弥补现行教材中的不足,教师可以在例题讲解中可以适当增加一些应用性的实例,引导学生去分析,进行模型求解。这样既培养了学生数学建模的意识,又让学生体会到将高等代数知识应用到实际中去的魅力所在,大大增加学生学习高代的兴趣。

例如,教师在讲解矩阵乘法与逆矩阵的应用之后,可以补充下面例子:

例2[8]在密码学中将明文消息通过一些处理使其隐藏起来成为密文,又可以通过矩阵将密码破译。密码在商业与军事中是一种保密通信技术,密码在保密通信技术中发挥了重要作用。

假设要发出的信息为“THE MESSAGE IS WRONG”。规定每个字母对应数字为26个字母,例如A对应1、C对应3。另外,空余的位置可以用0来表示。于是就有数集

{23,8,4,16,4,19,19,1,7,9,19,23,17,15,14,7}

表示“THE MESSAGE IS WRONG”,将其写成4行4列的行列式形式为:

(5)

密码发送者和接收者的共同基本矩阵为

(6)

通过变成矩阵被加密的信息再传输过程中以AM的形式输出,接收者收到的矩阵:

(7)

收到消息后计算A-1C来破译信息,还原出C即可得到原始信息。

这道例题是矩阵乘法与逆矩阵的应用,它不仅使学生熟悉所学知识,也会让学生了解信息科学发展,从而引发学生的学习兴趣。

同样,教师在讲解线性方程组时,也可以增加如下例题:

例3 投入产出模型。设甲,乙,丙3个部门组成一个经济系统,各部门生产满足系统内部和外部的需求,同时也消耗系统内部各部门的产品,如表2所示。

表2中,甲部门那一行的0.4表示该部门的1元钱产品需消耗甲部门的产品0.4元,其余类似。

1) 求y1,y2,y3与x1,x2,x3的关系

2) 当y1,y2,y3分别为40亿元,24亿元,16亿元时,求x1,x2,x3及z1,z2,z3。

解 1) 根据题意可得

(8)

2) 当y1=40,y2=24,y3=16时,由式(8),可解得x1=232,x2=212,x3=178。又因为

(9)

代入x1,x2,x3,可解得z1= 23.2,z2=21.2,z3= 35.6。

表2 直接消耗系数表

于是,通过简单的实例让学生感受到学好高等代数的必要性与重要性。

1.2.3 在课后作业及考核中引入数学建模思想

目前高等院校《高等代数》课程教学考试与课后习题多以理论知识为主,很少涉及应用与实践性的题目。这就导致了学生高分低能现象的出现,很难将所学知识应用到实际生活中。为改变学生学习的现状,应该在考核方式,评分标准与课后作业的类型题上做一定的改革。在考试中可以适当的增加一些开放性的应用题,要求学生以数学建模的方式来解答。在课后习题中可以给学生留一些需要实践验证的数学建模问题。让学生亲自观察并将结果记录下来,并判断计算结果是否正确,让学生体会到“做中学”的魅力。通过这样模式不但能够加深学生对所学内容的掌握程度,又能培养学生开拓创新、互帮互助的合作精神。这样的改革使高等代数这门课程重在积累、重在平时、重在知识的应用。

2 注重对学生学习方法的指导

基于数学建模思想的高等代数课程,能让学生更好地将高等代数应用到科学技术和生产活动中,体会到数学的重要性,达到事半功倍的学习效果。但是由于高等代数不是专门的数学建模课程,所以在教学中,教师可以引入代表性强的例题,不需按照完整的建模程序教学,而是传输数学建模的思想,以此达到让学生深入理解高等代数内容的目的。

3 结 语

将数学建模思想融入到高等代数中去,对提高学生知识的直观理解、和数学知识的实际应用的认识有较大的影响[8],能够给予学生更多独立思考的时间与机会,对于提升创新思维和实践能力具有非常重要的意义。这种新的教学方法目前还受到固有的教学方式影响故想要进一步实施还将面临巨大的挑战,想要深入的实现课程改革与适应还需要广大教师与学者的不断努力。

[1]王菡. 数学建模思想融入高数课堂的实践案例研究及分析[J]. 数学学习与研究, 2015(21):27-28.

[2]杨刘. 在《高等代数》课程教学中融入数学建模思想研究[J]. 探索与实践, 2013(13):236-237.

[3]JOSEPH J R. Advanced Modern Algebra[M]. London:Prentice Hallm, 2002.

[4]李大潜. 将数学建模思想融入数学类主干课程[P]. 中国大学数学, 2006(1):9-11.

[5]龚雅玲. 数学建模思想在高等数学教材中的渗透[J]. 北京教育学院学报(自然科学版), 2015(3):4-8.

[6]韦程东,周桂升,薛婷婷. 在高等代数教学中融入数学建模思想的探索与实践[J]. 高教论坛, 2008,4:28-30.

[7]郭秀英. 《高等代数》在数学建模中的应用举例[P]. 科技信息, 2013(24):2-2.

[8]王艳慧,宋毅. 数学建模思想渗入代数课程教学的试验研究----短周期课堂教学试验与分析[J]. 数学建模及其应用, 2015,4(1):55-59.

Research of advanced algebra teaching based on mathematical modeling thought

LI Li1, YANG Fangbai2, MEN Tongyu1, TANG Jiayue1

(1. College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China; 2. College of Mathematics, Liaoning Normal University, Dalian 110034, China)

This paper discusses how to integrate mathematical modeling thoughts into advanced algebra teaching in order to help the students understand the content of advanced algebra more deeply. But the examples involving in the teaching of advanced algebra can rarely link to the real life,some student feel the learning content abstract and disconnect with the real. This can not reflect the application of mathematics. By integrating the mathematical modeling thoughts into teaching,we analyze experimental data and establish models. This can translate the abstract knowledge into intuitive image. In the way,we can cultivate the students' innovative thinking and mathematics application consciousness. At the same way,this can improve the quality of teaching and the mathematics quality of the students.

mathematical modeling; advanced algebra; teaching, application of mathematics

1673-5862(2017)02-0253-04

2016-12-25。

辽宁省科技厅自然科学基金资助项目(2015020029)。

李 丽(1979-),女,辽宁锦州人,沈阳师范大学讲师,博士。

G642

A

10.3969/ j.issn.1673-5862.2017.02.024