花岗岩崩岗区不同土层的侵蚀水动力学特征*

王秋霞丁树文，2†邓羽松刘丹露徐加盼朱慧鑫刘昌鑫

（1 华中农业大学资源与环境学院，武汉 430070）

（2 农业部长江中下游耕地保育重点实验室，武汉 430070）

花岗岩崩岗区不同土层的侵蚀水动力学特征*

王秋霞1丁树文1，2†邓羽松1刘丹露1徐加盼1朱慧鑫1刘昌鑫1

（1 华中农业大学资源与环境学院，武汉 430070）

（2 农业部长江中下游耕地保育重点实验室，武汉 430070）

土壤剥蚀率是单位时间单位面积水流剥蚀土壤的质量，定量研究崩岗不同土层土壤剥蚀率对预测土壤剥蚀过程及建立崩岗侵蚀物理模型具有重要的理论和实践意义。针对湖北通城花岗岩崩岗区发育的表土层、红土层、砂土层、碎屑层，采用不同坡度（8.8%、17.6%、26.8%、36.4%、46.6%）和不同流量（0.2 L s-1、0.4 L s-1、0.6 L s-1、0.8 L s-1、1.0 L s-1）相结合的室内放水冲刷试验，分析表土层、红土层、砂土层、碎屑层土体土壤剥蚀率与水动力学参数之间的关系，初步探讨花岗岩崩岗侵蚀的水动力学机制。结果表明：在一定坡度条件下，土壤剥蚀率随径流流量的增大而增大，且各土层土壤剥蚀率存在很大差异，碎屑层土壤剥蚀率最大，砂土层次之，表土层最小；在相同流量条件下，各土层土壤剥蚀率均随冲刷时间的延长逐渐降低并趋于稳定；径流剪切力、水流功率对崩岗各土层土壤剥蚀率的影响均可采用线性方程很好地描述（R2＞0.926），相比用单位水流功率拟合的多项式方程的相关性（R2＜0.830）要高，径流剪切力和水流功率均可作为描述崩岗各土层土壤侵蚀的水动力学参数。表土层、红土层、砂土层、碎屑层的临界径流剪切力依次减小，分别为0.28Pa、0.13Pa、0.10Pa、0.07Pa，各土层土壤细沟可蚀性参数差异明显，碎屑层的最大，砂土层次之，表土层最小。因此，在崩岗垂直结构上，随着土层深度的增加，土体抵抗径流剥蚀的能力逐渐减弱。

崩岗；土壤剥蚀率；放水冲刷试验；水动力学参数

土壤剥蚀是土壤分离、搬运、沉积过程中的重要环节。目前，众多学者在WEEP水蚀预报模型、EUROSEM模型、LISEM模型和GUEST模型的基础上研究建立了不同实验条件下土壤剥蚀率与水流剪切力、单位水流功率、水流功率等水力学参数间的关系。1965年，Lyle和Smerdon［1］首次采用水槽试验阐述了土壤剥蚀率与径流剪切力之间的关系；Elliot和Laflen［2］、McIsaac等［3］认为水流功率能够准确地预测土壤剥离能力；随后，Govers［4］通过室内模拟冲刷试验研究发现水流剥蚀过程与单位水流功率的关系最紧密；Nearing等［5］、张光辉等［6-7］、蔡强国等［8］、张乐涛等［9］通过变坡水槽实验研究发现水流功率是描述坡面水流土壤剥蚀能力最好的水动力学参数，是坡面侵蚀的动力根源［5-9］；张科利和唐克丽［10］根据变坡水槽试验，建立了基于水流剪切力的径流剥蚀能力公式；黄炎和等［11］对崩岗崩积体进行室内放水冲刷试验表明单位水流功率可作为冲刷侵蚀的水动力学参数；蒋芳市等［12］对崩岗崩积体进行分离试验研究发现水流功率和水流剪切力可以很好地描述崩积体土壤剥蚀速率；柳玉梅等［13］详细研究了水深、平均流速、雷诺数、佛汝德数和阻力系数对土壤剥离能力的定量影响，得出平均流速是预测土壤剥蚀能力的最佳参数；王军光等［14］、王瑄等［15］分别对第四纪黏土发育红壤及陕西杨凌当地塿土利用冲刷试验研究发现土壤剥蚀率与流量、坡度呈幂函数关系，利用流量和坡度的幂函数可以准确地预测土壤剥蚀率［14-15］。以上分析表明，由于试验对象和研究手段的不同，坡面侵蚀的水动力学特征有很大差异。

崩岗是指在水力和重力综合作用下山坡土体受破坏而崩塌和冲刷的侵蚀现象，属于复合侵蚀类型［16-17］。崩壁是崩岗系统中最活跃的部位，崩壁侵蚀直接影响崩岗的严重程度以及侵蚀面积的扩大［18-20］。其主要形成原因是崩岗各土层土壤极其显著的可蚀性差异［21-22］。崩壁各层土壤理化性质的垂直分异特征可能对土壤剥蚀过程产生影响，但并不清楚其影响过程，需要进一步研究。目前，国内关于黄土高原坡面土壤剥蚀试验的研究较多，而关于南方花岗岩崩岗区各土层土壤侵蚀水动力参数指标的选定及侵蚀动力机制尚不明确，研究采取何种形式的水动力学参数作为判别崩岗各土层土体侵蚀过程具有重要的实际意义。因此，本项研究利用变坡水槽试验，分析崩岗各土层土体土壤剥蚀率与流量、坡度的关系，建立各土层土壤剥蚀率与各水力学参数之间的函数方程，阐明崩岗侵蚀的水动力学机理。

1 材料与方法

1.1 研究区概况

研究区位于湖北省东南部咸宁市通城县，地跨113°36′～114°4′E，29°2′～29°24′N。属于北亚热带季风气候区，气候温和，雨量充沛，全县平均气温为16.7℃，日最高气温为39.7℃，最低气温为-15.2℃，年平均降雨量1 550 mm。土壤类型为红壤。覆盖植被类型为常绿阔叶与落叶阔叶混交林为主。县域内崩岗发育较明显，总数量达1 120处，占湖北省崩岗总数的47%，是崩岗集中分布的典型区域。

根据崩岗土壤剖面的发生层次，采取湖北通城花岗岩崩岗区发育典型的表土层、红土层、砂土层、碎屑层土样，对各土层土壤性质进行分析（表1）。

1.2 实验设计

试验采用移动式可调坡钢制冲刷水槽，尺寸为3.8 m×0.2 m×0.2 m（长×宽×高），水槽顶端设有规格大小为0.4 m×0.2 m×0.4 m稳水箱用于调节流入水槽的水流稳定、均匀，水槽下端距出口20 cm处有一土样室，规格为：内径14 cm，深10 cm。试验对象为崩岗各土层原状土，设置流量为0.2 L s-1、0.4 L s-1、0.6 L s-1、0.8 L s-1和1.0 L s-1，坡度为8.8%、17.6%、26.8%、36.4%、46.6%，共100个处理，每个处理重复2次。共进行有效试验200场次。

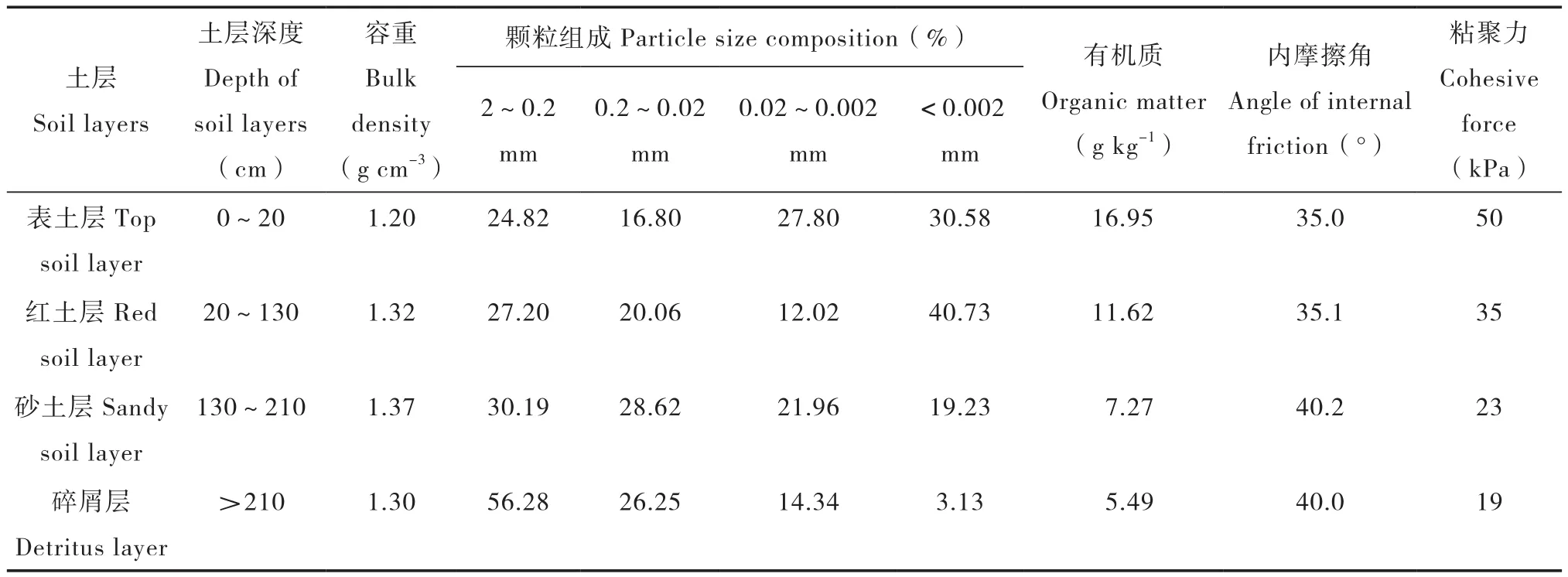
表1 试验土壤基本性质Table 1 Basic properties of the experimental soil

用直径14 cm、高10 cm、厚度3 mm的钢制环刀采集花岗岩崩岗区不同土层的原状土。将采集的环刀土样放入容器内饱和（逐渐向容器内加水，水面低于土样表面0.5 cm，放置12 h）；实验前将水流流量和坡度调至设计流量和坡度，并多次人工率定水流流量，以保证流量的准确性。试验冲刷前将供试环刀土样放入水槽下端的土样室内，尽量使土样表面与水槽底部保持相同高度。采用高锰酸钾染色法测定水流流速。试验冲刷时间根据流量大小和土壤质地确定。即每10 s用大塑料桶接泥沙样，间隔20 s后再接泥沙样，30 s为一个周期，当冲刷土样深度达到2 cm或冲刷过程中土壤结构严重破坏时，结束试验，记录冲刷时间，沉积泥沙样在105 ℃下烘干称重。

实验所得数据通过SPSS18.0进行统计分析，使用Origin8.0进行图表制作。

1.3 数据分析

（1）土壤剥蚀率（Dr）基于全部塑料桶内的泥沙样计算而得，计算公式如下：

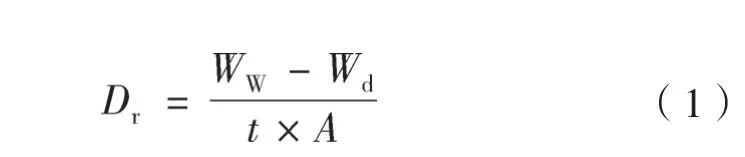
式中，Dr为土壤剥蚀率（kg m-2s-1）；WW为实验前土壤的干土重（kg）；Wd为试验后土壤的干土重（kg）；A为土壤样本表面积（m2）。

（2）径流剪切力（τ）：径流剪切力是反映径流在流动时对坡面土壤剥蚀力的参数。

式中，τ为径流剪切力，Pa或N m-2；γm为浑水密度，kg m-3，考虑了含沙量的影响；g为重力加速度，9.8 m s-2；R为水力半径，m，用水深代替；J为水力能坡，用坡度的正弦值近似代替。

（3）水流功率（ω）：径流功率表征作用于单位面积的水流所消耗的功率，反映剥蚀一定量土壤所需功率。

式中，ω为水流功率，N m-1s-1；V为坡面平均水流流速，为观测时段内所测流速的平均值并乘以流速修正系数k所得的值（层流，k=0.67；过渡流，0.70；紊流，k=0.80），m s-1。

（4）单位水流功率（P）：作用于泥沙床面的单位重量水体所消耗的功率。

式中，P为单位水流功率，m s-1。

2 结果与讨论

2.1 土壤剥蚀率随冲刷时间的变化规律

土壤剥蚀是土壤侵蚀发生的初始阶段，是指径流剥蚀地表土粒脱离原土体的过程。分析5个流量、5个坡度条件下各土层土体的冲刷数据表明：各土层土壤剥蚀率均随坡度和流量的增大而增大，在不同流量、不同坡度下，剥蚀率均随冲刷时间的延长而减小。以坡度17.6%为例，根据实验数据绘制了崩岗各土层土壤在不同流量条件下剥蚀率随时间的变化过程（图1）。从图中可以得出：同一坡度下，径流冲刷流量越大，土壤剥蚀率越大，大流量（0.8 L s-1、1.0 L s-1）条件下的土壤剥蚀率显著高于小流量（0.2 L s-1、0.4 L s-1）下的土壤剥蚀率；各土层土壤剥蚀率存在很大差异，碎屑层土壤剥蚀率最大，砂土层次之，表土层最小；各土层土壤剥蚀率均随冲刷时间的延长逐渐降低并趋于稳定，其中表土层剥蚀率大致在30 s时达到稳定，红土层和砂土层均在50 s时达到稳定，碎屑层稍有波动。这可能由于碎屑层发育程度较低，0.2～2 mm颗粒组成较多，土壤容重较小，有机质含量低，土体稳定性较弱，水流较易携带表面土壤脱离土体本身，被剥蚀的土壤砂粒含量较多，这些砂粒被剥蚀搬运的同时带动周边砂粒脱离土体表面，随着水流流量和坡度的增大，被剥蚀的土壤急剧增多；表土层中＜0.02 mm的细颗粒组成较多，土壤容重小，土壤有机质含量高且结合紧密，粘聚力较大，水流不易携带0.2～2 mm粒径的土壤脱离表面土壤；红土层颗粒组成主要为粉粒，水流携带＜0.02 mm的土壤粒径脱离表面土壤的能力相对较小。因此，各土层土壤基本性质对土壤剥蚀率的影响比较明显。有机质含量高，细颗粒含量高的土壤剥蚀率较低。各土层土壤剥蚀率在整个冲刷过程中均出现多次交叉，这可能由于在冲刷过程中随着流量的增大，土壤剥蚀率增加，水流动能增大，随着冲刷时间的延长，各土层土壤被水流侵蚀下切的深度增加至能被剥蚀的土壤越来越少，且水流所受周围的摩擦阻力不稳定，水流动能消耗不均一。该研究结果与张光辉［23］关于普通褐土土壤剥蚀率随着冲刷时间变化关系的研究结果略有不同，张光辉的相关研究成果中剥蚀率随冲刷时间呈良好的幂函数形式下降，且建立了最佳冲刷时间与坡度、流量的幂函数关系。

2.2 流量和坡度对土壤剥蚀率的影响

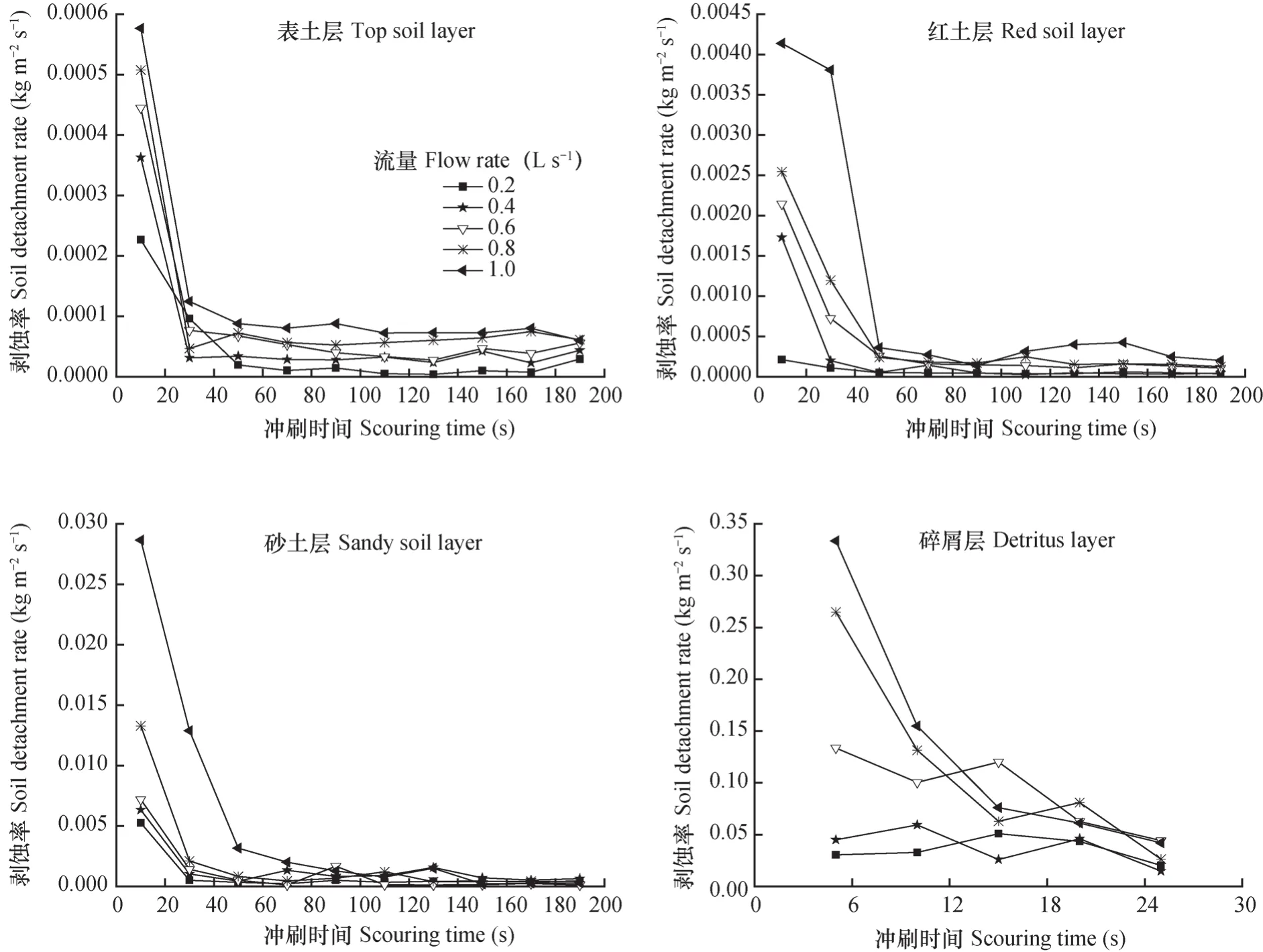
图1 坡度17.6%时各土层土体不同流量条件下剥蚀率变化曲线Fig. 1 Variation of soil detachment rate with flow rate on slopes 17.6% in degree relative to soil layers

由各土层土体在5个流量（0.2 L s-1、0.4 L s-1、0.6 L s-1、0.8 L s-1、1.0 L s-1）和5个坡度（8.8%、17.6%、26.8%、36.4%、46.6%）条件下的冲刷数据可知：随着坡度和流量的增加，各土层土壤剥蚀率的增大逐渐加快，这可能由于在水流沿水槽坡面向下流动过程中，水流的重力势能和动能被水槽底部及侧壁的摩擦力做功所损耗。在小坡度范围内水流的总能量较小，用于克服摩擦力做功后所剩余的总能量更小，即水流剥蚀土壤的能力减弱，土壤剥蚀率随坡度增大而增加的速率较缓，在大坡度范围内，水流动能增大，更多的势能转化为动能，总能量急剧增加，用来克服摩擦力做功后所剩余的总能量依然很大，即土壤剥蚀率随坡度增大而增加的速率较快。同理，小流量时土壤剥蚀率随水流流量的增加而增加的速率较缓，大流量时，土壤剥蚀率随流量的增加而增加的速率较快。因此，有必要进一步定量分析流量和坡度对崩岗各土层土壤剥蚀率的影响，对崩岗各土层土壤剥蚀率随坡度和流量变化的试验数据进行多元统计分析，得出不同坡度及流量下各土层土体剥蚀率因子模型（表2）。

由表2可以看出崩岗各土层土壤剥蚀率可用二元幂函数方程很好地拟合（R2＞0.878）。所得各土层因子模型能够很好地描述流量、坡度两个因子对土壤剥蚀率的影响；通过相关分析对各土层方程进行显著性检验表明：坡度与流量两个因子与各土层土壤剥蚀率呈极显著相关关系（p＜0.01）。因此，土壤剥蚀率因子模型可以用来计算水流对崩岗各土层土体剥蚀分离的能力。该因子模型与Zhang等［7］和申楠［24］提出的水流剥蚀能力因子模型一致。

表2 各土层土壤剥蚀率因子模型Table 2 Factor model for soil detachment rate relative to soil layer

2.3 土壤剥蚀率与各水力学参数之间的关系

目前关于代表坡面水流能量的水动力学参数较多，有单一的水动力因子（流速、流量、水深、加速度等），也有综合几个水动力因子的复合参数形式（雷若数、弗罗德数、水流剪切力、水流功率等）。其中，剪切力和功率是影响泥沙输移的最主要水流强度指标［25］，因此，本试验主要研究分析的水动力学参数为：径流剪切力、水流功率和单位水流功率。

坡面水流的侵蚀能力与水流的剪切应力之间有着密切关系，坡面水流的剪切力反映的是坡面运动的水流对土水界面上土壤颗粒的分散、剪切作用，它是径流剥蚀土壤的主要动力［26］。径流恰好克服土粒间作用力时的剪切力称之为临界剪切力，超过临界剪切力的那一部分剪切力才真正地对剥离土壤起作用，径流的剥蚀能力应该是大于临界剪切力部分的水流切应力，称之为有效剪切力［5，27］。可用下式表示：

式中，Dr为土壤剥蚀率，kg m-2s-1；Kr为细沟可蚀性参数，s m-1，与土壤性质有关；τr为临界水流剪切力，Pa。

根据试验数据，绘制了不同坡度条件下崩岗各土层土体的径流剪切力与土壤剥蚀率之间的关系，如图2所示。

对各土层土壤剥蚀率与径流剪切力进行回归分析，如表3：

图2 各土层土壤剥蚀率与坡面径流剪切力的关系Fig. 2 Relationship between runoff shear stress and soil detachment rate relative to soil layers

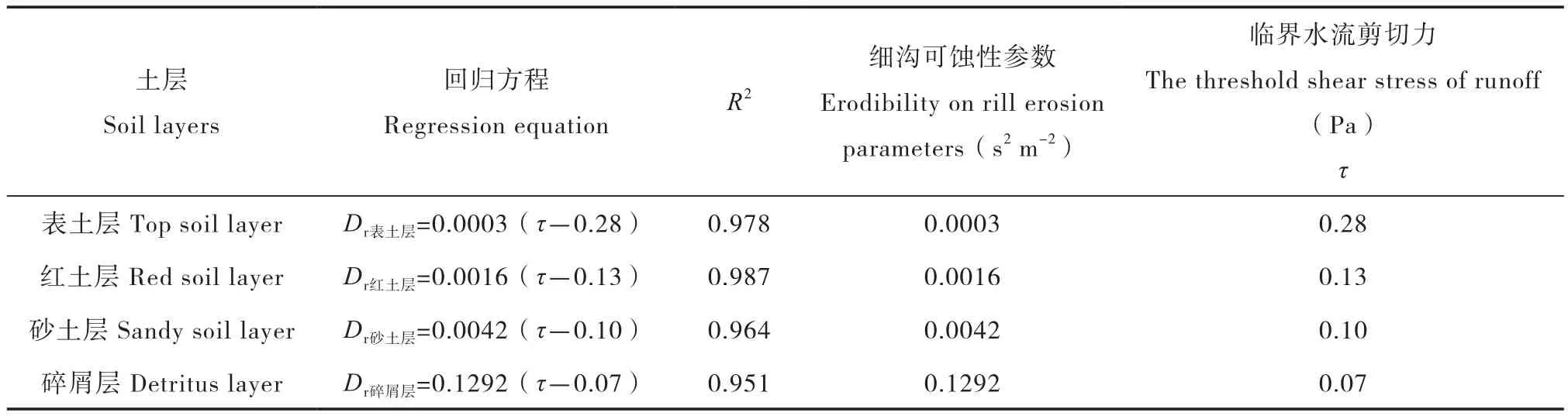
表3 各土层土壤剥蚀率与临界径流剪切力之间的回归方程Table 3 Regression equations for soil detachment rate and shear stress of different soil layers

图3 各土层土壤剥蚀率与坡面水流功率的关系Fig. 3 Relationship between stream power and soil detachment rate relative to soil layers

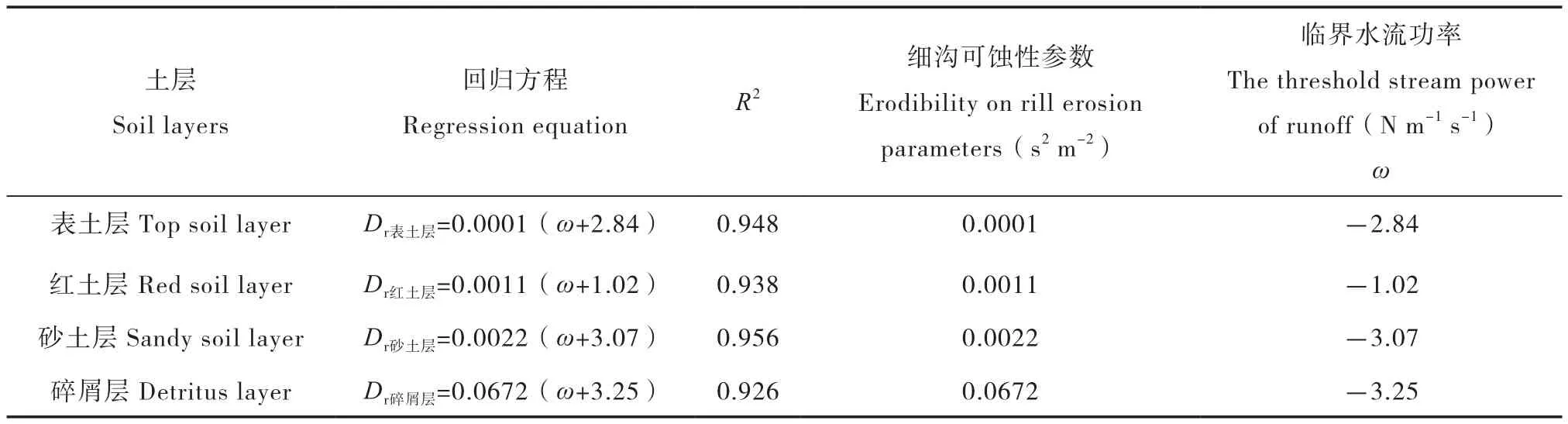
表4 各土层土壤剥蚀率与水流功率之间的回归方程Table 4 Regression equations for soil detachment rate and stream power relative to soil layers

由表3可知各土层土壤剥蚀率均随径流剪切力呈线性增长（R2＞0.951）。径流剪切力越大，土壤剥蚀率越高，土壤侵蚀越严重，当有效剪切力相等时，碎屑层的土壤剥蚀率最大，砂土层次之，表土层的最小；表土层、红土层、砂土层和碎屑层的临界径流剪切力差异明显，碎屑层的临界径流剪切力最小，土壤较易被剥离分散；碎屑层的细沟可蚀性参数最大，为砂土层的30.80倍，红土层的381.1倍，表土层的487.4倍，这可能由于碎屑层土壤抗侵蚀能力较弱，抗剪强度较弱，土体不稳定，较易被剥离分散。由此可知，在崩岗形成过程中，崩壁垂直结构上随着深度的增加，土壤的临界水流剪切力逐渐减小，细沟可蚀性参数逐渐增加，抗侵蚀能力逐渐减弱，下层土体较易被剥离、分散、沉积，随着侵蚀时间的延长，下层土体逐渐被掏空，上层土体在自身重力作用下发生垮塌，进一步促进了崩岗的发育。与耿晓东［28］在坡度8.8%、17.6%、26.8%、36.4%、46.6%，降雨量50～100 mm h-1条件下对黄土、红壤及紫色土的研究结果比较，本实验碎屑层水流剪切力相对应的细沟可蚀性参数较大，且各层土壤的临界水流剪切力均小于黄土、红壤及紫色土。本实验得到的临界水流剪切力在0.07～0.28 Pa之间，是张光辉等［29-30］相关研究成果的1/10，表明崩壁各层土壤较易发生侵蚀崩塌。

水流功率是径流剪切力与流速的乘积，从能量学角度反映的是径流分散、剪切土壤颗粒作用中的功率大小，表征水流损失能量而做功的速率，是影响侵蚀的重要水动力学参数［2］。崩岗各土层土壤剥蚀率与水流功率之间的关系如图4所示。水流功率可用下式表示：

式中，Kd为细沟可蚀性参数，s2m-2，与土壤性质有关；ωc为临界水流功率，N m-1s-1。

对各土层土壤剥蚀率与水流功率进行回归分析，如表4。

由表4可知，崩岗各土层土壤剥蚀率均随水流功率呈线性增长（R2＞0.926）。水流功率越大，土壤剥蚀率越高，土壤流失越严重。在相等水流功率作用下，碎屑层的土壤剥蚀率最大，砂土层次之，表土层的最小；各土层中碎屑层的细沟可蚀性参数最大，为砂土层的30.55倍，红土层的60.24倍，表土层的487.2倍。各土层土壤临界水流功率均出现负值。这可能由于在整个试验过程中，水力侵蚀不再是坡面产流产沙的唯一原因，随着坡度的变化重力侵蚀强度逐渐增加。

单位水流功率表征单位质量水体势能随时间的变化率。说明单位质量的水体输移泥沙的功率与水体本身具有的功率直接相关。Moore等［31］通过试验研究证明单位水流功率可以直接用于坡面侵蚀过程，但还缺乏临界单位水流功率和适应土壤类型的研究。因此，根据试验数据绘制了各土层土壤剥蚀率与单位水流功率之间的关系。如图5所示。

对各土层土壤剥蚀率与单位水流功率（P）进行回归分析，如表5。

由表5可知：各土层土壤剥蚀率均可拟合成多项式方程，且与王瑄等［15］的研究结果类似。但各土层的相关系数不高（R2＜0.830）。说明径流冲刷条件下各土层土壤剥蚀率与单位水流功率关系不紧密。单位水流功率不能准确地描述崩岗各土层土壤剥蚀率。

3 结 论

本试验研究中崩岗各土层土壤剥蚀率不是受某单一因子的影响，而是受流量和坡度的综合作用，且各土层土壤剥蚀率均能用坡度和流量的二元幂函数很好地拟合。径流剪切力、水流功率与各土层土壤剥蚀率之间均存在良好的线性关系，且相关性较高；各土层土壤均出现临界径流剪切力，随着土层深度的增加，临界径流剪切力逐渐减小，抗侵蚀能力逐渐减弱，下层土体较易被水蚀。同时，水蚀过程促进龛的形成，随着龛的不断扩大，崩壁上层土体在重力作用下发生崩塌，加速溯源侵蚀进程，导致崩岗不断扩大；同时，在不同坡度及流量条件下各土层土体临界水流功率均为负值，这进一步说明了水力不是导致侵蚀发生的唯一原因，崩岗是水力和重力综合作用的一种复合侵蚀类型。

图4 各土层土壤剥蚀率与坡面单位水流功率的关系Fig. 4 Relationship between unit stream power and soil detachment rate relative to soil layers

表5 各土层土壤剥蚀率与单位水流功率之间的回归方程Table 5 Regression equation for soil detachment rate and unit stream power relative to soil layers

［1］ Lyle W M，Smerdon E T. Relation of compaction and other soil properties to erosion resistance of soils. Transactions of the ASAE，1965，8（3）：419—422

［2］ Elliot W J，Laflen J M. A process-based rill erosion model. Transactions of the ASAE，1993，36（1）：65—72

［3］ McIsaac G F，Mitchell J K，Hummel J W，et al. An evaluation of unit stream power theory for estimating soil detachment and sediment discharge from tilled soils. Transactions of the ASAE，1992，35（2）：535—544

［4］ Govers G. Relationship between discharge velocity and flow area for rills eroding loose，non-layered materials. Earth Surface Processes and Landforms，1992，17 （5）：515—528

［5］ Nearing M A，Simanton J R，Norton L D，et al. Soil erosion by surface water flow on a stony，semiarid hillslope. Earth Surface Processes and Landforms，1999，24（8）：677—686

［6］ 张光辉，刘宝元，张科利. 坡面径流分离土壤的水动力学试验研究. 土壤学报，2002，39（6）：882—886

Zhang G H，Liu B Y，Zhang K L. Experimental simulation of hydraulic mechanism of soil detachment by surface runoff on slope land（In Chinese）. Acta Pedologica Sinica，2002 39（6）：882—886

［7］ Zhang G H，Liu B Y，Nearing M A，et al. Soil detachment by shallow flow. Transactions of the ASAE，2002，45（2）：351—357

［8］ 蔡强国，陆兆熊，王贵平. 黄土丘陵沟壑区典型小流域侵蚀产沙过程模型. 地理学报，1996，51（2）：108—117

Cai Q G，Shiu-hung Luk，Wang G P. Process-based soil erosion and sediment yield model in a small basin in the hilly loess region（In Chinese）. Acta Geographica Sinica，1996，51（2）：108—117

［9］ 张乐涛，高照良，田红卫. 工程堆积体陡坡坡面土壤侵蚀水动力学过程. 农业工程学报，2013，29（24）：94—102

Zhang L T，Gao Z L，Tian H W. Hydrodynamic process of soil erosion in steep slope of engineering accumulation （In Chinese）. Transactions of the CSAE，2013，29 （24）：94—102

［10］ 张科利，唐克丽. 黄土坡面细沟侵蚀能力的水动力学试验研究. 土壤学报，2000，37（1）：9—15 Zhang K L，Tang K L. A study on hydraulic characteristics of flow for prediction of rill detachment on capacity on loess slope（In Chinese）. Acta Pedologica Sinica，2000，37（1）：9—15

［11］ 黄炎和，赵淦，蒋芳市，等. 崩岗崩积体陡坡侵蚀的水动力学特征. 森林与环境学报，2015，35（4）：304—309

Huang Y H，Zhao G，Jiang F S，et al. Hydrodynamic characteristics in steep colluvial deposits slope（In Chinese）. Journal of Forest and Environment，2015，35（4）：304—309

［12］ 蒋芳市，黄炎和，林金石，等. 坡面水流分离崩岗崩积体土壤的动力学特征. 水土保持学报，2013，27 （1）：86—89

Jiang F S，Huang Y H，Lin J S，et al. The dynamic characteristics of soil detachment of slumping deposit by surface runoff in Benggang（In Chinese）. Journal of Soil and Water Conservation，2013，27（1）：86—89

［13］ 柳玉梅，张光辉，李丽娟，等. 坡面流水动力学参数对土壤分离能力的定量影响. 农业工程学报，2009，25 （6）：96—99

Liu Y M，Zhang G H，Li L J，et al. Quantitative effects of hydro-dynamic parameters on soil detachment capacity of overland flow（In Chinese）. Transactions of the CSAE，2009，25（6）：96—99

［14］ 王军光，李朝霞，蔡崇法，等. 坡面流水力学参数对团聚体剥蚀程度的定量影响. 水科学进展，2012，23 （4）：502—508

Wang J G，Li Z X，Cai C F，et al. Quantitative effects of hydro-dynamic parameters on abrasion extent aggregates by overland flow（In Chinese）. Advances in Water Science，2012，23（4）：502—508

［15］ 王瑄，李占斌，尚佰晓，等. 坡面土壤剥蚀率与水蚀因子关系室内模拟试验. 农业工程学报，2008，24 （9）：22—26

Wang X，Li Z B，Shang B X，et al. Indoor simulation experiment of the relationship between soil detachment rate and water erosion factor（In Chinese）. Transactions of the CSAE，2008，24（9）：22—26

［16］ 阮伏水. 福建省崩岗侵蚀与治理模式探讨. 山地学报，2003，21（6）：675—680 Ruan F S. Study on slump gully erosion and its control in Fujian Province（In Chinese）. Journal of Mountain Science，2003，21（6）：675—680

［17］ 丁树文，蔡崇法，张光远. 鄂东南花岗地区重力侵蚀及崩岗形成规律的研究. 南昌工程学院学报，1995，S （1）：50—54

Ding S W，Cai C F，Zhang G Y. A study on gravitational crosion and the formation of collapse mound in the granite area of Southeast Hubei（In Chinese）. Journal of Nanchang Institute of Technology，1995，S （1）：50—54

［18］ 刘希林，张大林. 基于三维激光扫描的崩岗侵蚀的时空分析. 农业工程学报，2015，31（4）：204—211

Liu X L，Zhang D L. Temporal-spatial analyses of collapsed gully erosion based on three-dimensional laser scanning（In Chinese）. Transactions of the CSAE，2015，31（4）：204—211

［19］ 牛德奎. 崩岗侵蚀调查方法的探讨. 江西水利科技，1994，20（1）：42—47

Niu D K. Approach to the methods of surveying collapsing hill erosion（In Chinese）. Jiangxi Hydraulic Science & Technology，1994，20（1）：42—47

［20］ 林敬兰，黄炎和，蒋芳市. 崩岗土体的渗透性能机理研究. 水土保持学报，2013，27（2）：53—56

Lin J L，Huang Y H，Jiang F S. Study on the mechanism of different soil layer’s permeability in Benggang（In Chinese）. Journal of Soil and Water Conservation，2013，27（2）：53—56

［21］ 邓羽松，丁树文，刘辰明，等. 鄂东南花岗岩崩岗崩壁土壤水分特征研究. 水土保持学报，2015，29（4）：132—137

Deng Y S，Ding S W，Liu C M，et al. Soil moisture characteristics of collapsing gully in granite area of southeastern Hubei（In Chinese）. Journal of Soil and Water Conservation，2015，29（4）：132—137

［22］ 张勇，丁树文，万绍文，等. 黄麻土工布对不同层次土体的水土保持效用分析. 水土保持学报，2014，28 （4）：23—28

Zhang Y，Ding S W，Wan S W，et al. Effect analysis of soil and water conservation of Jute Geotextile on the different layers of soil（In Chinese）. Journal of Soil and Water Conservation，2014，28（4）：23—28

［23］ 张光辉. 冲刷时间对土壤分离速率定量影响的实验模拟. 水土保持学报，2002，16（2）：1—4

Zhang G H. Experimental simulation on effects of scouring time on soil detachment rate（In Chinese）. Journal of Soil and Water Conservation，2002，16 （2）：1—4

［24］ 申楠，王占礼，陈浩. 黄土坡面细沟水流分离能力. 山地学报，2015，33（2）：191—198

Shen N，Wang Z L，Chen H. Soil detachment capacity of rill flow on loess hillslope（In Chinese）. Journal of Mountain Science，2015，33（2）：191—198

［25］ 田凯，李小青，鲁帆，等. 坡面流侵蚀水动力学特性研究综述. 中国水土保持，2010（4）：44—47

Tian K，Li X Q，Lu F，et al. Summary of hydrodynamic characteristics of overland flow erosion（In Chinese）. Soil and Water Conservation in China，2010（4）：44—47

［26］ 雷廷武，张晴雯，赵军. 陡坡细沟含沙水流剥蚀率的试验研究及其计算方法. 农业工程学报，2001，17 （3）：24—27

Lei Y W，Zhang Q W，Zhao J. Laboratory experiments and computational method of soils detachment rate of sediment loading flow in rills（In Chinese）. Transactions of the CSAE，2001，17（3）：24—27

［27］ 张科利，彭文英，杨红丽. 中国土壤可蚀性值及其估算. 土壤学报，2007，44（1）：7—13

Zhang K L，Peng W Y，Yang H L. Soil erodibility and its estimation for agricultural soil in China（In Chinese）. Acta Pedologica Sinica，2007，44（1）：7—13

［28］ 耿晓东. 主要水蚀区坡面土壤侵蚀过程与机理对比研究. 北京：中国科学院研究生院，2010

Geng X D. Comparative study on hill slope soil erosion processes and mechanisms in main water erosion regions of China（In Chinese）. Beijing：University of Chinese Academy of Sciences，2010

［29］ 张光辉，刘宝元，何小武. 黄土区原状土壤分离过程的水动力学机理研究. 水土保持学报，2005，19（4）：48—52

Zhang G H，Liu B Y，He X W. Study on hydro-dynamic mechanism of natural soil detachment in loess region（In Chinese）. Journal of Soil and Water Conservation，2005，19（4）：48—52

［30］ 何小武，张光辉，刘宝元. 坡面薄层水流的土壤分离试验研究. 农业工程学报，2003，19（6）：52—55

He X W，Zhang G H，Liu B Y. Soil detachment by shallow flow on slopes（In Chinese）. Transactions of the CSAE，2003，19（6）：52—55

［31］ Moore I D，Burch G J. Sediment transport capacity of sheet and rill flow：Application of unit stream power theory. Water Resources Research，1986，22（8）：1350—1360

Hydrodynamic Characteristics of Erosion in Different Soil Layers in Granite Collapse Region

WANG Qiuxia1DING Shuwen1，2†DENG Yusong1LIU Danlu1XU Jiapan1ZHU Huixin1LIU Changxin1
（1 College of Resources and Environment，Huazhong Agricultural University，Wuhan 430070，China）
（2 Key Labrortory of Arable Land Conservation for Middle and Lower Reaches of Yangtze River，Ministry of Agriculture，Wuhan 430070，China）

【Objective】Soil detachment rate refers to the quantity of soil detached by water flow in a unit of time and/or area. Quantitative analyses of the soil detachment processes in different soil layersin granite collapse regions is of great theoretical and practical significance to accurate prediction of soil detachment processes and construction of a physical model for erosion of collapsed hills.【Method】Collapsing hill erosion is a specific type of soil erosion in hilly granitic regions of tropical and subtropical South China，and may result in extremely rapid water and soil loss. Knowledge of how collapsing hill erosion affects the soil physical and chemical properties of different soil layers in the region is important to understanding the evolution of soil quality. In this study，an in-lab runoff scouring experiment was conducted on artificial slopes of top soil layer，red soil layer，sandy soil layer and detritus layer developed in the collapsed granite hills in Tongcheng，Hubei Province. The runoff scouring experiment had the slopes set at 8.8%，17.6%，26.8%，36.4% and 46.6% in gradient and scoured with flow varying in rate（0.2 L s-1，0.4 L s-1，0.6 L s-1，0.8 L s-1and 1.0 L s-1），separately for cross checking . The artificial slope was prepared on a steel trough 0.2 m high on both side，0.2 m wide and 3.8 m long and on the top of the trough was a water tank，0.2 m high，0.4 m wide and 0.2m long，filled with water to supply water flow steadily at a required rate. The experiment was to investigate relationships of soil detachment rate with various hydrodynamics parameters in four different soil layers and to explore hydrodynamic mechanisms of the erosion in collapsing granite hills.【Result】Results show that under the condition of a certain slope，soil detachment rate increased with increasing runoff flow rate，and varied sharply with soil layer；the highest detachment rate was found in the detritus layer，which was followed by sandy soil layer，red soil layer and top soil layer；under the same runoff flow rate，soil detachment rate decreased with the scouring going on and tended to level off，regardless of type of soil layers. Besides，the complex effect of slope degree and flow rate on detachment rates in all soil layers could be well fitted with the two-variable power function equation （R2＞0.878）. The effects of shear stress and stream power of the runoff on detachment rate on all soil layers could be well described with the linear equation（R2＞0.926），yielding a correlation coefficient much higher than that of the fitting of unit stream power with the polynomial equation（R2＜0.830）. Therefore，shear stress and stream power of the runoff can be used as hydrodynamic parameters to describe the soil erosion in different soil layers of collapsed hills. The threshold of runoff shear stress varied with soil layer in a decreasing order of top soil layer＞red soil layer＞sandy soil layer＞detritus layer or 0.28 Pa＞0.13 Pa＞0.10 Pa＞0.07 Pa.【Conclusion】The detritus layer is the highest in erodibility，followed by the sandy soil layer，red soil layer and top soil layer. Hence，the resistance of the soil layers against runoff erosion gradually decreases with soil depth as the soil layers exist vertically in the soil profile in the collapsing hill region.

Collapsed gully；Soil detachment rate；Runoff scouring experiments；Hydrodynamics parameters

S157.1

A

（责任编辑：檀满枝）

* 国家自然科学基金项目（41571258）资助 Supported by the National Natural Science Foundation of China（No.41571258）

† 通讯作者 Corresponding author，E-mail：dingshuwen@mail.hzau.edu.cn

王秋霞（1991—），女，河南周口人，硕士研究生，主要从事花岗岩风化土可蚀性及崩岗稳定性研究。

E-mail：qxwangchn@163.com

2016-07-14；

2016-09-28；优先数字出版日期（www.cnki.net）：2017-01-09

10.11766/trxb201607140306