基于熵权法和改进TOPSIS模型的水资源配置综合评价

郭 磊

(新疆塔里木河流域希尼尔水库管理局， 新疆 库尔勒 841000)

基于熵权法和改进TOPSIS模型的水资源配置综合评价

郭 磊

(新疆塔里木河流域希尼尔水库管理局， 新疆 库尔勒 841000)

水资源配置方案的合理确定对区域经济社会可持续发展意义重大。本文利用熵权法对水资源配置评价指标合理赋权，结合改进TOPSIS模型，对某地区水资源配置方案进行综合评价。结果表明：该方法计算科学简单,结果合理可信，能够有效应用于水资源配置方案的综合评价。

水资源配置； 熵权法； TOPSIS模型； 综合评价

水资源是一种重要的自然资源，作为国家、社会发展和人类生存的物质基础，具有不可替代的作用。水资源配置是从流域和区域整体出发，从经济、社会、资源、环境等多方面协调配置用水量，开展水资源配置方案的综合评价研究具有十分重要的理论和实际应用价值。目前，关于水资源配置方案评价的研究主要有模糊综合评价法、能值分析法、可拓物元模型、集对分析法[1]等，这些方法各有特点，但在具体的应用过程中都存在一定的局限性，且模型精度较难控制。

鉴于此，本文在前人研究的基础上，建立了基于熵权与改进TOPSIS模型的水资源配置评价方法，以解决评价过程中信息量不全、难以定量和准确性不高的问题。

1 水资源配置评价体系构建

1.1 评价指标体系构建及权重确定

1.1.1 评价指标体系构建

从社会、经济、资源及效率合理性4个方面构建评价指标体系，遵循代表性、可操作性、可量化性原则，共选取10个指标表征水资源配置方案效果(见表1)。

表1 水资源配置综合评价指标体系

1.1.2 指标权重确定

采用熵权法确定。熵权法是一种由待评价指标来确定指标权重的一种客观评价法，具有较强的操作性，能够有效反映数据隐含的信息，增强指标的差异性和分辨性，以避免选取指标的差异过小而造成的分析不清，从而达到全面反映各类信息的目的[2]。熵权法的评价思路是评价对象在某项指标的值相差越大，该对象越重要，权重值较大。根据指标变异程度，客观计算出各指标的权重值，为多个指标的综合评价提供更为可靠的依据。计算步骤如下：

a.将判断矩阵归一化处理，得到归一化判断矩阵B：

(1)

式中 xmax、xmin——同指标下不同方案中最满意者和最不满意者。

b.根据熵的定义，m个方案n个评价指标，可确定评价指标的熵为

(i=1,2,…,m； j=1,2,…,n)

(2)

(3)

评价指标的熵权W：

(4)

1.2 评价模型构建

TOPSIS(technique for order preference by similarity to ideal solution)模型由Hwang和Yoon在1981年提出，是系统工程中有限方案多目标决策分析的一种决策技术，为距离综合评价法[3]。近年来，该模型被用于风险决策分析、土地生态安全评价等多个方面[4]，取得了较好的成果。该模型的优点在于能够充分利用原始数据、计算过程数据丢失量较小、几何意义直观且不受参考序列选择的干扰。“正理想解”和“负理想解”是TOPSIS模型中的两个重要概念，即通过寻求各个指标中的最优解和最劣解，构建评价指标与最优解和最劣解之间距离的二维数据空间，在此基础上对各评价指标与最优解和最劣解作比较，如果在最接近最优解的同时又最远离最劣解，则该方案为待评价方案中的最优方案，反之，则为最差方案。

本文将改进的TOPSIS模型与熵权法相结合，用于评价水资源配置方案效果。与传统的TOPSIS模型相比，改进的TOPSIS模型主要是将待评价对象与最优解和最劣解的评价值公式进行了改进。具体步骤如下：

a.数据标准化处理。通常运用极值标准化法对评价指标进行处理，用以确定具体指标实际值在该指标权重中所处的状况，可以直接利用熵权法中确定的标准化矩阵B。

b.确定指标权重，建立加权决策矩阵。将前面介绍的熵权法的权重向量wj考虑到决策矩阵中，通过标准化矩阵B与其权重wj相乘得到加权后规范化决策矩阵为V=(vij)m×n：

(5)

c.寻求正理想解和负理想解。令B+表示最优方案(正理想解)，B-表示最劣方案(负理想解)，则有：

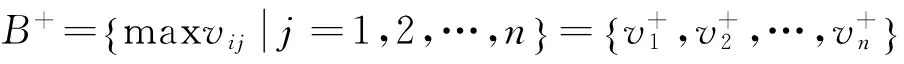
(6)

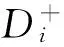
(7)

e.计算各方案与理想解的相对贴近度Ci：

(8)

根据Ci值的大小排序，Ci越大则方案越优。

2 模型应用

2.1 基本资料

根据吴征等[5]的研究数据，采用改进TOPSIS法对研究区水资源配置方案进行综合评价。水资源配置各方案评价指标值见表2。

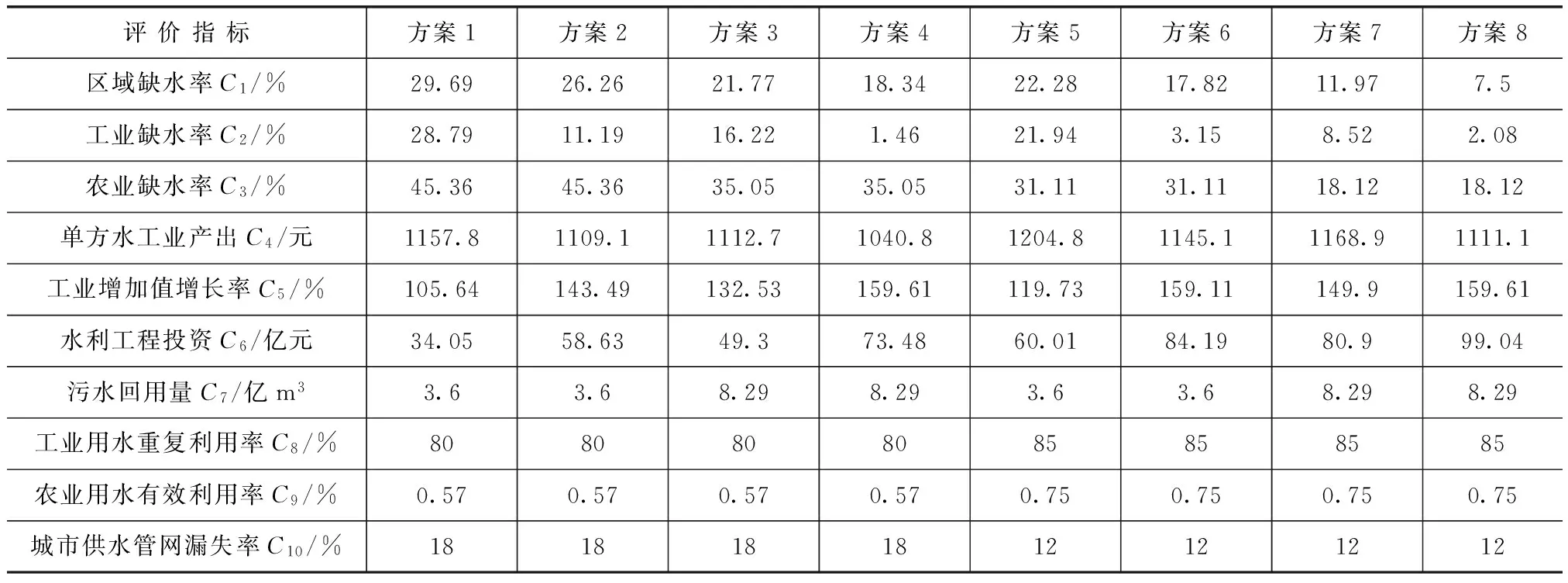
表2 水资源配置各方案评价指标值

2.2 评价指标权重计算

根据式(1)计算得到各方案评价指标的归一化值见表3。

表3 各方案评价指标归一化值

根据表3，利用式(2)～式(4)得到各评价指标的熵，并由此确定评价指标的权重W=(0.0872，0.0719，0.0992，0.0673，0.0703，0.0773，0.1301，0.1322，0.1328，0.1317)。

2.3 模型评价

利用式(5)～式(8)得到各评价方案的正负理想解距离及贴近度见表4。

表4 水资源配置方案评价

根据表4评价结果可知，方案8的贴近度为0.8936，为最优方案；方案7的贴近度为0.8893，为次优方案。基于熵权TOPSIS法的水资源配置综合评价结果为：方案8>方案7>方案6>方案5>方案4>方案3>方案2>方案1(>表示优于)。该研究结果与吴征等[5]的研究结果完全一致，表明本文所用方法科学可靠。

3 结 论

a.通过指标权重排序，在影响水资源配置评价的

各项指标中，污水回用量、工业用水重复利用率、农业用水有效利用率及城市供水管网漏失率为重要指标，其权重分别为0.1301、0.1322、0.1328与0.1317，对评价结果影响大；工业缺水率、单方水工业产出、工业增加值增长率和水利工程投资为边缘指标(即次要指标)，对评价结果影响弱。

b.将熵权法和改进TOPSIS模型应用于水资源配置方案评价，结果表明方案8为最优方案，方案7为次优方案，这与其他方法的研究结果完全一致，实现了方法对方法的检验。

[1] 屈国栋.区域水资源合理配置及方案综合效益评价研究[D].杭州:浙江大学,2013.

[2] 程启月.评测指标权重确定的结构熵权法[J].系统工程理论与实践,2010,30(7):1225-1228.

[3] HWANG C L,YOON K.Methods for multiple attribute decision making[M]//Multiple Attribute Decision Making.Germany:Springer Berlin Heidelberg,1981:58-191.

[4] TSAUR R C.Decision risk analysis for an interval TOPSIS method[J].Applied Mathematics & Computation,2011,218(8):4295-4304.

[5] 吴征,吴凤平,沈俊源.基于集对分析法的水资源配置方案综合评价[J].灌溉排水学报,2016,35(12):73-79.

Comprehensive evaluation on water resources allocation based on entropy weight method and improved TOPSIS model

GUO Lei

(Xinjiang Tarim River Basin Administration Xi’ni’er Reservoir Administration, Korla 841000, China)

Reasonable determination of water resources allocation plans has important significance for sustainable development of regional economy and society. In the paper, the entropy weight method is utilized for reasonable empowerment on water resources allocation evaluation indicators. Improved TOPSIS models are combined for comprehensive evaluation of water resources allocation plans in one region. Results show that calculation by the method is scientific and simple; the result is reasonable and reliable, which can be efficiently applied for evaluating water resources allocation plans comprehensively.

water resources allocation; entropy weight method; TOPSIS model; comprehensive evaluation

10.16616/j.cnki.10-1326/TV.2017.05.017

TV211.1

A

2096-0131(2017)05- 0070- 04