基于直觉模糊决策算法的排课系统选择研究

郑爱媛 林 峰

(福建商学院， 福州 350012)



基于直觉模糊决策算法的排课系统选择研究

郑爱媛 林 峰

(福建商学院， 福州 350012)

针对属性信息为直觉模糊数且属性信息之间存在相互关系的排课系统选择问题，构建了一种基于广义直觉模糊加权Heronian几何(GIFWHG)算子的直觉模糊多属性决策算法。该算法首先基于Archimedean范数和Heronian平均，提出了广义直觉模糊Heronian几何(GIFHG)算子，并探讨了GIFHG算子的基本性质和几种常见形式，同时引入GIFWHG算子，最后构建了新的直觉模糊多属性决策算法，通过自动排课系统的选择实例验证了该算法的可行性和有效性。

直觉模糊集； 决策算法； Heronian平均； Archimedean范数； 排课系统选择

排课系统对于学校的决策者和管理者来说都至关重要。排课系统管理中一个非常重要的课题就是排课系统的选择问题，而排课系统的选择问题本质上是一个多属性群决策问题[1]。

多属性决策算法是现代决策理论的重要组成部分[2]。1986年，保加利亚学者Atanassov提出了直觉模糊集[3]，其本质是模糊集[4]的一种广义形式。在直觉模糊环境下，文献[5]基于算术平均算子定义了运算法则，并且建立了一系列直觉模糊信息集成算子方法。基于自信度概念，文献[6]研究了自信直觉模糊加权平均算子、自信直觉模糊加权几何算子。在直觉模糊数的隶属函数与非隶属函数中引入概率和函数及比例分配规则，文献[7]构造了直觉模糊加权中性平均算子、直觉模糊加权中性几何算子。针对决策信息为区间直觉梯形模糊数的MADM问题，文献[8]提出了一种基于区间直觉梯形模糊几何加权Heronian平均算子的决策方法。这些运算法则都是基于Algebraic范数提出的，而Algebraic范数只是Archimedean范数的一种运算形式[10]，该算法可使决策过程中的决策方法更加灵活，从而做出科学合理的决策。

此次研究基于Archimedean范数，提出一种新的GIFHG算子，并且研究其性质，同时探讨GIFHG算子的几种常用形式及其加权形式，最后构建直觉模糊多属性决策算法，并用自动排课系统选择实例对提出的决策方法进行验证。

1 基本理论知识

1.1 直觉模糊集

定义1[3]设X是一个非空集合，X上的一个直觉模糊集定义为

A={(x,μA(x),νA(x))|x∈X}

(1)

式中：μA(x)、νA(x)分别表示X上元素x属于集合A的隶属度和非隶属度，且满足

0≤μA(x)+νA(x)≤1

为了计算方便，称α=(μ,ν)=(μA(x),νA(x))为一个直觉模糊数(IFN)[5]，它的补为αc=(ν,μ)。

定义2[5]设α=(μ,ν)是一个IFN，那么称Δ(α)=μ-ν和Φ(α)=μ+ν分别为α的得分函数和精确函数。若αi=(μi,νi)(i=1,2)为两个IFNs，则有：

(i) 若Δ(α1)>Δ(α2)，那么α1>α2；

(ii) 若Δ(α1)=Δ(α2)，那么 (a)当Φ(α1)>Φ(α2)时，α1>α2； (b)当Φ(α1)=Φ(α2)时，α1=α2。

1.2 基于Archimedean范数的运算法则

由文献[10]可知，严格Archimedean T范数可由一个严格递减的加性算子g(·)表示为T(x,y)=g-1(g(x)+g(y))，其中g(1)=0,g(0)=1。基于对偶性质，有S(x,y)=h-1(h(x)+h(y))，其中h(t)=g(1-t)。因为g(t)严格单调递减，则h(t)为严格单调递增函数，且h(0)=0,h(1)=1[10]。

定义3[11]设α=(μ,ν),α1=(μ1,ν1),α2=(μ2,ν2)为IFNs，则有

(i)α1⊕α2=[h-1(h(μ1)+h(μ2)),g-1· (g(ν1)+g(ν2))]

(ii)α1⊗α2=[g-1(g(μ1)+g(μ2)),h-1· (h(ν1)+h(ν2))]

(iii)λα=[h-1(λh(μ)),g-1(λg(ν))]λ>0

(iv)αλ=[g-1(λg(μ)),h-1(λh(ν))]λ>0

1.3 Heronian平均

定义4[12]假设ai(i=1,2,…,n)为一组非负实数，且p,q>0，则Heronian平均满足如下形式：

(2)

2 GIFHG算子及其性质

由于直觉模糊决策算法中需要将某一个备选方案在不同指标属性下的决策信息进行综合集结，并且考虑属性指标间的内在联系，提出广义直觉模糊Heronian几何算子，并探究其基本性质。

定义5 令αi(i=1,2,…,n)为一列IFN，且参数p,q>0，则称

(3)

为广义直觉模糊Heronian几何算子，简记为GIFHG算子。

基于定义3中的运算法则，有如下结论成立。

定理1 令αi=(μi,νi)(i=1,2,…,n)为一列IFNs，参数p,q>0，则运用GIFHG算子得到的集成结果为IFN，且满足

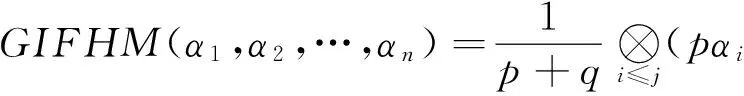
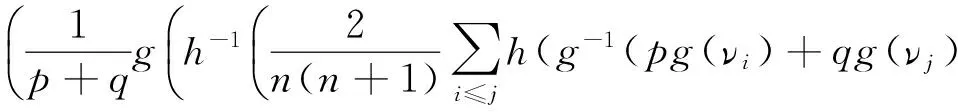
(4)

下面探讨GIFHG算子满足的一些性质。

性质1 (幂等性)若所有的IFNαi(i=1,2,…,n)相等，即对∀i=1,2,…,n，有αi=α，那么

GIFHG(α1,α2,…,αn)=α

(5)

性质2 (单调性)对任意两列IFNαi,βi(i=1,2,…,n)，如果有μαi≤μβi,ναi≥νβi(i=1,2,…,n)，那么

GIFHG(α1,α2,…,αn)≤GIFHG(β1,β2,…,βn)

(6)

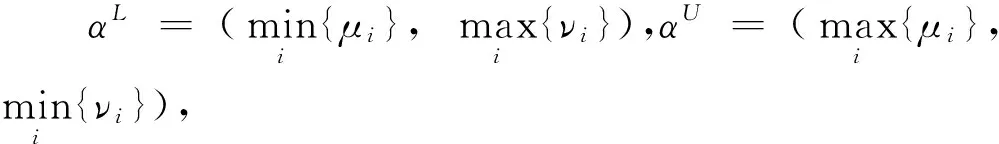
αL≤GIFHG(α1,α2,…,αn)≤αU

(7)

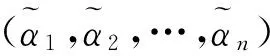
(8)

3 几种常用GIFHG算子及其加权形式

研究对加性算子g(t)和参数p,q赋予不同的函数和数值时，得到GIFHG算子的几种常用形式，同时给出GIFHG算子的加权形式。

3.1 赋予g(t)不同的函数

Case1 令g(t)=-lg(t)，那么GIFHG算子转变为直觉模糊Heronian几何(IFHG)算子：

IFHG(α1,α2,…,αn)

(9)

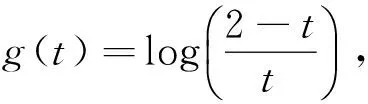
(10)

其中

3.2 参数p,q赋予不同的实数值

Case1 若q→0，那么GIFHG算子退化为广义直觉模糊几何(GIFG)算子：

(11)

Case2、若p=1且q→0，那么GIFHG算子退化为直觉模糊几何(IFG)算子：

(12)

Case3、若p=q=1，那么GIFHG算子变为广义直觉模糊交互平方Heronian几何(GIFISHG)算子：

(13)

3.3 GIFHG算子的加权形式

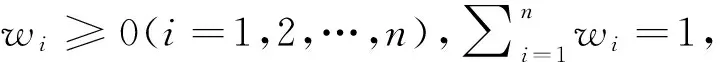
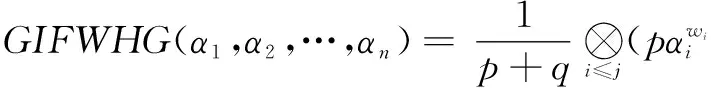
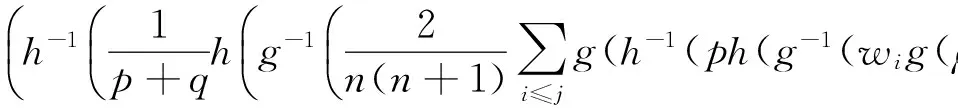
(14)

为广义直觉模糊加权Heronian几何(GIFWHG)算子。

4 基于直觉模糊决策算法的排课系统选择及其应用

4.1 基于直觉模糊决策算法的排课系统选择

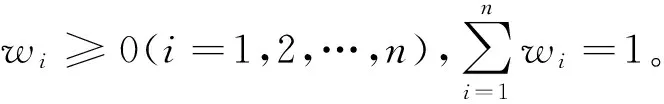
利用GIFWHG算子处理上述排课系统选择问题的步骤如下：

步骤1：通过以下方法将矩阵D=(αij)m×n转化为标准直觉模糊决策矩阵B=(βij)m×n：

(15)

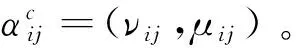
步骤2：运用GIFWHG算子计算各排课系统Xl的综合属性值βl。

步骤3：分别计算各综合属性值βl(l=1,2,…,m)的得分函数Δ(βl)和精确函数Φ(βl)，并将综合属性值βl(l=1,2,…,m)进行大小排序。

步骤4：基于综合属性值βl(l=1,2,…,m)的排序结果对各排课系统进行优劣排序，并选择综合性能最优的排课系统。

4.2 案例分析

某高校计算机与信息学院为了响应学校自动化办公的号召，欲面向市场购买1套自动排课系统[12]。经过前期的简历筛选和初审，现有4套自动排课系统Xi(i=1,2,3,4)符合条件可供选择。为了从这4套自动排课系统中选择出1套综合性能最高的自动排课系统，由该校人事部门和学院领导组成的专家小组将对这4套自动排课系统进行各方面性能评估，包括系统效率C1、排课合理性C2和系统替代性C3，且这3个属性指标的权重向量为w=(0.3,0.4,0.3)Τ。已知自动排课系统在上述属性指标下的评价偏信息为αij=(μij,νij)，于是所有的评价信息构成一个直觉模糊决策矩阵D=(αij)4×3，见表1。

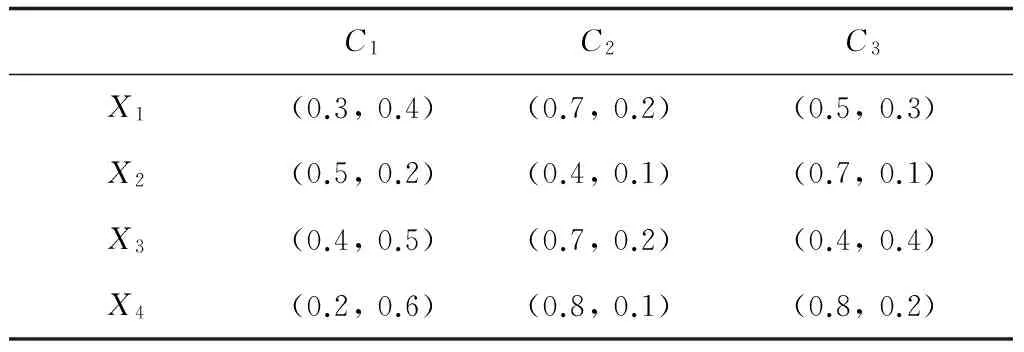
表1 直觉模糊决策矩阵D

运用提出的排课系统选择方法对自动排课系统进行排序，并选择出综合性能最高的自动排课系统。

步骤1：由于属性指标Ci(i=1,2,3)均为效益型指标，因此不需要对决策矩阵D进行标准化处理。

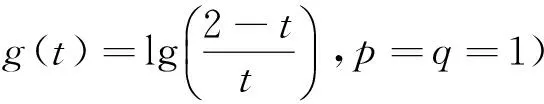
α1=(0.374 1,0.295 0)

α2=(0.437 5,0.129 1)

α3=(0.356 9,0.358 2)

α4=(0.422 2,0.260 0)

步骤3：分别计算各综合属性值αl(l=1,2,3,4)的得分函数Δ(αl)(l=1,2,3,4)，结果如下：

Δ(α1)=0.079 1Δ(α2)=0.308 3

Δ(α3)=-0.001 3Δ(α4)=0.162 3

因为Δ(α2)>Δ(α4)>Δ(α1)>Δ(α3)，所以α2>α4>α1>α3，从而这4套自动排课系统的综合性能由高到低的排序为X2、X4、X1、X3，即综合性能最高的自动排课系统为X2。该决策方法具有以下优点：

(1) 该决策方法考虑到了决策过程中输入的属性信息存在相互关系的情形，这使得决策结果更加合理可靠。

(2) 在决策过程中，对于参数p,q的选择可以依据决策者的主观态度的变化而改变。同时，选择什么样的参数(p,q)，也能够判断决策者是冒险型、保守型和中立型中的哪一种类型。

(3) 该决策方法适用的范围更为广泛。当加性算子和参数取不同的函数与数值时，可以得到不同的算子进行信息的集成。

5 结 语

本次研究在直觉模糊环境下，结合Archimedean范数，并运用Heronian平均，提出了一种GIFHG算子，其能够在信息集成过程中充分考虑到属性信息值之间的内在联系。探讨了GIFHG算子的性质和几类特殊平均及其加权算子形式。最后基于提出的GIFWHG算子构建了一种新的直觉模糊决策算法，并将其应用于自动排课系统选择过程中，验证了该决策方法的可行性与有效性。

[1] 张艳红,王玲玲,腾东兴.基于空间模型和遗传算法的高校排课系统[J].计算机系统应用,2015,24(9):49-55.

[2] 李二涛.基于一致性改进算法的电子政务信息共享模式研究[J].重庆科技学院学报(自然科学版),2016,18(5):82-85.

[3] ATANASSOV K T. Intuitionistic Fuzzy Sets [J]. Fuzzy Sets and Systems,1986,20(1):87-96.

[4] ZADEH L A. Fuzzy Sets [J]. Information and Control, 1965,8(3):338-356.

[5] XU Z S. Intuitionistic Fuzzy Aaggregation Operators [J]. IEEE Transactions on Fuzzy Systems, 2007, 15(6): 1179-1187.

[6] YU D J. Intuitionistic Fuzzy Information Aaggregation Under Condence Levels [J]. Applied Soft Computing,2014,19:147-160.

[7] HE Y D, CHEN H Y, HE Z, et al. Multi-attribute Decision Making Based on Neutral Aaveraging Operators for Intuitionistic Fuzzy Information [J]. Applied Soft Computing,2015,27:64-76.

[8] 周晓辉,姚俭.区间直觉梯形模糊几何Heronian平均算子及应用[J].计算机工程与应用,2016,52(9):39-43.

[9] CHU Y C, LIU P D. Some Two-dimensional Uncertain Linguistic Heronian Mean Operators and Heir Application in Multiple-attribute Decision Making [J]. Neural Computing and Applications,2015,26:1461-1480.

[10] DESCHRIJVER G, COMELIS, KERRE E E. On the Representation of Intuitionistic Fuzzy T-norms and T-conorms [J]. IEEE Transactions on Fuzzy Systems,2004,12:45-61.

[11] XIA M M, XU Z S, ZHU B. Some Issues on Intuitionistic Fuzzy Aggregation Operators Based on Archimedean T-conorm and T-norm [J]. Knowledge-Based Systems, 2012,31:78-88.

[12] BELIAKOV G, PRADERA A, CALVO T. Aggregation Functions: A Guide for Practitioners[M].Berlin: Springer, 2007:30-45.

Research on Selection of Course Arranging System Based on Intuitionistic Fuzzy Decision Making Algorithm

ZHENGAiyuanLINFeng

(Fujian Commercial College, Fuzhou 350012, China)

When attribute values are in the form of intuitionistic fuzzy numbers and attribute information is associated with each other, an intuitionistic fuzzy MADM algorithm is developed for selection of course arranging system, on the basis of the generalized intuitionistic fuzzy weighted Heronian geometric (GIFWHG) operator. Based on the Archimedean norm and Heronian mean, the generalized intuitionistic fuzzy Heronian geometric (GIFHG) operator is proposed, and then the properties and some special cases of the GIFHG operator are discussed. In addition, the GIFWHG operator is introduced. Finally, a novel intuitionistic fuzzy MADM algorithm is investigated, and applied to select auto-arranging course system to demonstrate the developed algorithm′s rationality and effectiveness.

intuitionistic fuzzy set; decision making algorithm; Heronian mean; Archimedean norm; selection for course arranging system

2017-01-20

国家自然科学基金项目“大数据环境下群体智能算法构架中的技术研究”(71571023)；2016年福建省中青年教师教育科研项目(科技类)“利用状态空间的启发式搜索法实现自动排课系统”(JAT160578)；福建省高校省级自然科学研究重点项目“直觉模糊环境下的决策算法研究和应用”(KJ2016A026)。

郑爱媛(1977 — )，女，讲师，研究方向为计算机软件开发与决策算法。

TP35

A

1673-1980(2017)03-0095-04