层级递归式模糊逻辑系统的建模

徐利谋 李长云 满君丰

(1. 中山火炬职业技术学院信息工程系， 广东 中山 528437；2. 湖南工业大学计算机与通信学院， 湖南 株洲 412007)



层级递归式模糊逻辑系统的建模

徐利谋1李长云2满君丰2

(1. 中山火炬职业技术学院信息工程系， 广东 中山 528437；2. 湖南工业大学计算机与通信学院， 湖南 株洲 412007)

针对传统模糊逻辑系统存在的问题，基于已知测量数据系统，提出了3种不同结构的层级递归式模糊逻辑系统，并使用Python语言验证了新型结构的可行性。在静态和动态不同模拟状况下，3种不同结构各有所长，具有不同应用空间。

模糊逻辑系统； 动态系统模拟； 静态函数模拟； 层级结构

动态系统的建模是过程系统工程中最重要的研究课题，模型的精准度直接影响系统的可行性与准确性[1]。传统的解析方法存在一定的局限性，基于经验和数据的近似算法应用越来越广泛，如人工神经网络、模糊逻辑系统等[2]，其中，基于规则的模糊逻辑系统能通过规则来描述动态系统，从而保证系统的描述简单且容易理解，受到研究者们越来越多的关注。规则所需的数据来源既可以是传感器的测量数据，也可以是人们的实践经验[4]。

模糊逻辑系统中模糊变量的数量代表了系统的精准度。但系统规则的数量与模糊变量的数量呈指数关系，过多的规则将破坏系统的透明性，从而使其失去模糊逻辑系统的优势。为了避免透明度与精准度之间的冲突，本次研究借鉴Cordon等人提出的基于规则层级式结构的概念，将变量空间分割为较少的子空间以提高系统的透明性。每一个子空间将自身区域内根据模糊变量的数量划分成对应的网格状，网点代表当前坐标下的规则，以提高系统的准确度。

1 建模理论基础

1.1 基于规则的模糊逻辑系统

传统逻辑使用的是二进制数，将事物描述成1和0。模糊逻辑在连续递进的过程中有更为精准的描述。模糊逻辑可以将人类的思维、决策用数学的方式表达成连续的逻辑真值函数，进而对某领域的经验性结论建立数学模型。在模糊逻辑中，一个元素可以一部分属于某个集合，这种关系将由隶属度函数来表达：

F=(x,μ(x)|x∈G∩μ(x)∈[0,1])

(1)

可以用来作为隶属度函数的函数有很多，但最常用的是三角型函数。在模糊逻辑中，逻辑运算符号也与传统逻辑有着细微差别[5]。基于规则的模糊逻辑中，规则结构为Mamdani模型[6]。在此模型中，Ai,j代表第i个变量的第j个模糊值，i∈ [1,n],j∈[1,l]。k∈[1,m]则表示系统中规则的序数，y则为规则对应的结论值。以下的5个步骤可以将语言或经验性规则转化成用模糊逻辑表达的数学规则，并得出相应结论：

(1) 知识或语言中变量的模糊化：确定隶属度函数值，即确定所有的值。

(2) 单个规则中模糊变量的集合：用最小值算子将一个规则中的所有变量组合起来，即：

μAjj,k(X1,X2,…,Xn)= min{(μAi,1(X1),μAi,j(X2),…,μAn,l(Xn)}

(2)

(3) 单个规则中前提和结论的推理：利用最小值算子，通过变量的集合结果来推断结论的隶属值，即：

μk(X1,X2,…,Xn)= min{μAij,k(X1,X2,…,Xn),μk(y)}

(3)

(4) 所有规则的组合：使用最大值算法将所有规则的结论组合起来，即：

(4)

(5) 结论的解模糊化：使用中心平均反模糊算子(CenterofSingleton)来计算结论的数值表达，即：

(5)

按照此种方式所得到的模糊逻辑模型，整个变量将根据模糊变量数和隶属度函数分布划分出方形子区间，区间的每个顶点都代表着一个规则。这些规则在较为复杂的系统中，规则数目将以指数形式递增，这也导致运算量极为庞大。为了避免这种由系统精确化带来的不便，这里将对系统的变量空间进行分层，每一层再进行分割，从而降低规则的总数，使计算和建模的运算成本降低。

1.2 系统结构优化

1.2.1 模糊C-均值算法

模糊C-均值算法(Fuzzy C Means, FCM)[7]可以在离线状态下，将数据点(L个)划分到不同集合中并优化每个集合的中心位置及隶属度函数，算法的具体步骤见流程。算法中所需的初始参数有：中心点的数量、终止条件ε、对比参数及一个随机的初始隶属度函数。对比参数α决定了隶属度函数边缘的模糊程度，α越大，边缘越模糊。根据测试需要，此算法在具体编程过程中的变量包含：模糊变量的变量数目、集合中心点数目、对比参数α、终止条件ε，α和ε为固定值，而其他2个参数将在测试中通过取得不同数值来检验建模效果。

1.2.2 沃罗诺伊区域分割

沃罗诺伊图是由沃罗诺伊所有中心点连线所构成的三角形的外心来确定的，每个中心点的沃罗诺伊区域如图1中粗线条围成的区域，加粗圆点处为子细胞顶点[8-9]。图1中浅色圆点间的连线所构成的三角形被称之为德劳内三角化。

德劳内三角化具有空间分割的唯一性和空圆特性，从而能保证变量空间中的每一个点都有且只有一个对应的德劳内三角，并只由此三角形的3个顶点处的规则所约束。这种约束力的计算，需要借助重心坐标[10]。图2为德劳内三角形中的重心坐标示意图。若q处于3个顶点所在的三角形中，那么存在以下关系：

(6)

而3个权重u,v,w由三角形面积A(x,y,z)来确定：

(7)

当处于3个顶点的规则值已知时，可以通过这种插值方式来确定当前的变量。如果当前坐标处于变量值域边缘，或恰好与某一沃罗诺伊中心重合时，将只有一个规则被激活并利用[8-9]。

图1 沃罗诺伊区域分割及其对应的德劳内三角图

图2 德劳内三角形中的重心坐标示意图

在每一个沃罗诺伊区域之中的变量空间将会使用传统的长方形网格方式来进一步分割细化，以保证系统的准确度。分割细化构成了双层结构中的下层结构[10-11]。本研究将采取不同参数优化算法应用于双层结构中的下层结构优化，即确定网格中所有规则结论值的优化。训练数据与模型当前值之间的方差将在计算中被最小化。优化算法将采用典型的线性算法，即最小二乘法，以及一个常用的非线性梯度下降法(Levenberg-Marquardt方法)来优化系统中的规则结论值。

最小二乘法是一种最为常用的线性最优值算法。通过对误差方差的求导，并对其一次导数为零的求解，就可得到方程的优化解。在一个方程中，如果B为已知变量数据矩阵，f为已知变量值矩阵，而c为未知向量，那么这个方程的最优解为：

c=(BTB)-1BTf

(8)

具体计算时，在一个有N个规则的模糊逻辑系统中，B是一个N×L的隶属度矩阵，它的横排代表一个训练数据中的所有变量隶属所有规则的程度，它的竖排则显示出训练数据组数。c作为一个1×N的向量，代表着本次优化中所有的规则值。对应着每个训练数据，所有被激活的规则及其隶属度函数乘积的总和除以隶属度函数总和之后，这个被标准化了的总和则构成了f变量值矩阵[9]：

(9)

加权最小二乘法与普通最小二乘法间的区别在于添加了一个权重系数θ。由于这个权重的存在，可以人工的控制哪些规则在计算中被激活[11]。而方程最优解则变成了：

c=(θBTB)-1θBTf

(10)

Levenberg-Marquardt方法组合了2种最优化方法于一体，即高斯牛顿法和梯度下降法。这种算法在当参数靠近最终结果时会优先选择高斯牛顿法，而在误差较大时则采用收敛速度更高的梯度下降法。本次研究中直接采用了Python库中存在的Levenberg-Marquardt方法[12]。

2 系统模拟

为了直接观察建模情况，并用较少的运算时间对比不同建模参数对建模结果进行比较，采用简单的非线性静态函数作为第一步建模目标。其后，为了检验这种模糊逻辑系统对于复杂动态系统建模的精准程度，还将对典型的钟摆模型的微分方程进行模拟和测试。

2.1 测试系统函数

2.1.1z=xysin(xy)函数

非线性静态函数z(x,y)的曲线见图3。模拟函数z不仅能通过3D图像来直接地观察模型的误差，且它只有2个变量，即变量空间为二维。二维变量空间可以方便地显示其相应的沃罗诺伊图和德劳内三角图，并用较低的运算成本即可以对比出不同参数下模型误差的大小。

2.1.2 钟摆模型

在系统识别和控制系统设计中，钟摆模型是一个典型的例子，其简化模型见图4。

图3 函数z=xysin(xy)的曲线

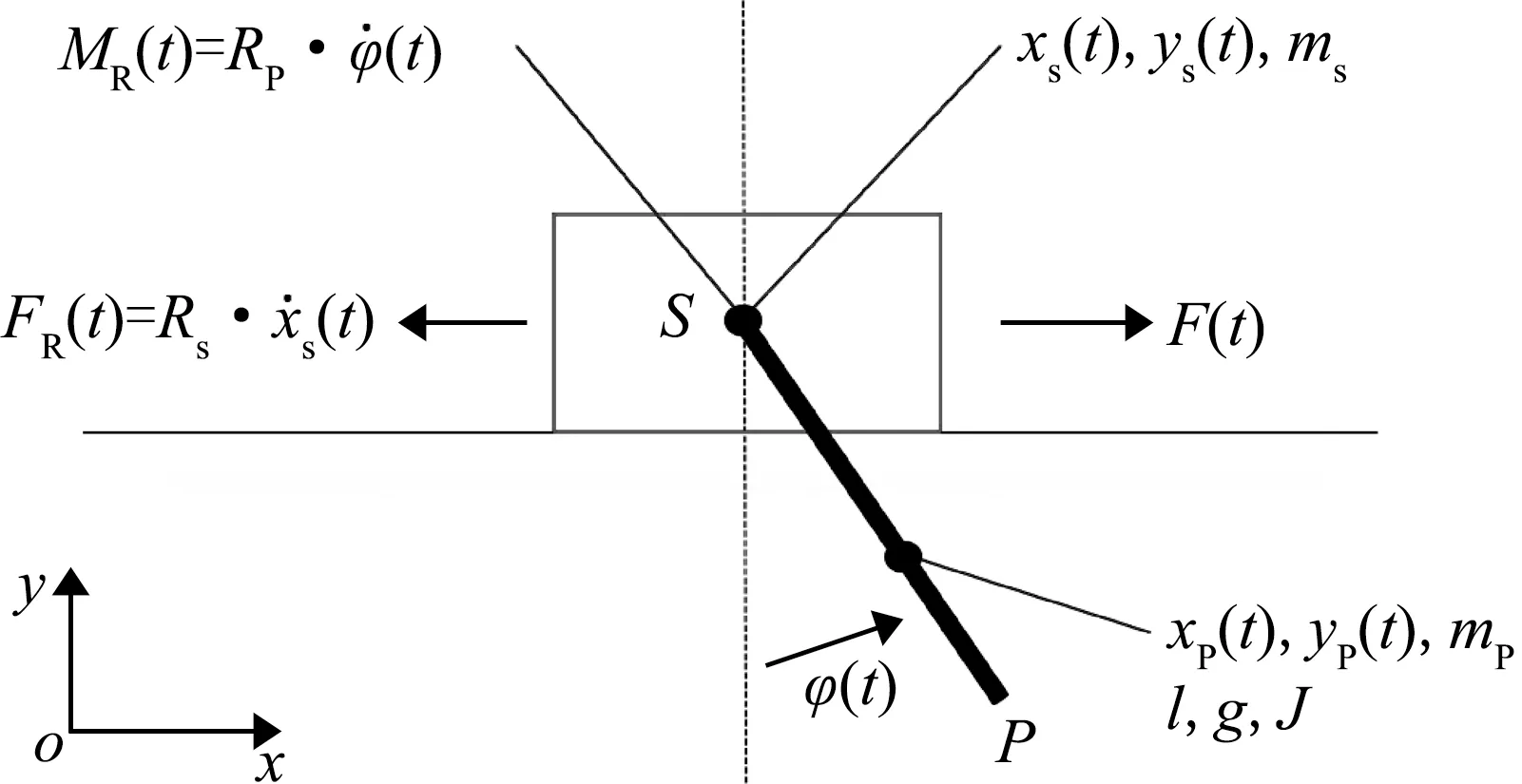
图4 钟摆模型简化图

物块S受到外力F(t)作用，从而使其位置xs(t)及其与钟摆P之间的夹角φ(t)发生变化。简化后的系统运动微分方程如下：

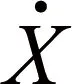
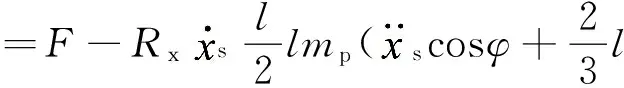
(11)

将上述方程转化为标准的离散状态空间表达方式，即：

x(k+1)=Ax(k)+Bu(k)
y(k)=Cx(k)+Du(k)

(12)

其中的状态输出向量为：

(13)

方程(11)中所有的系统常数取自于实验数据[13]，见表1。

2.2 人工生成训练数据

建模过程的第一步是通过1.1节中2个系统的数学模型人工地模拟传感器的测量数据，以便在以后步骤中使用此数据对模糊逻辑系统进行优化。静态函数所模拟出来的训练数据为3 000组，其定义域为x,y∈[-2, 2]。在此区间内的变量由随机函数生成，并保证两个随机变量没有相关性。生成的结果将被以[x,y,z]的格式保存在一个L×3的矩阵中。

表1 钟摆模型中的系统常数

由于建模结果只是变量空间中的规则值，在最后的误差计算中我们将重新生成1 000组检验数据，以保证检验数据与训练数据无相关性。这 1 000组数据将被优化过的模型进行计算，计算结果用来与函数值进行比较和误差分析。

2.3 上层结构设计

基于上述人工生成的测量数据，可以通过模糊C-均值算法(FCM)来建立模糊聚类。由于在试验过程中，对3 000组数据的计算用时已经超出了 24 h，将只采用1 000组数据对上述2个测试系统进行FCM计算，而且这1 000组数据与2.2节中的数据无相关性。对比参数α=2及误差下限值ε=10-7在整个实验过程中保持不变。集合中心点的数量即沃罗诺伊中心点的数量以及每个变量将在实验中取不同的数值以进行对比。上层结构的构成如图5所示。

图5 上层结构的构成

图5(a)中每一个子细胞内，都将根据变量的定义域中的离散值个数N将每一变量维度等距离划分成N-1部分，这个变量离散值数目将在本文中作为模拟测试中的第二个系统参数变量，见图5(b)。通过这样的划分，即可获得下层结构的基本网格，每个网点代表着模糊逻辑系统的规则，接下来将通过训练过程来确定这些规则的具体内容。

2.4 下层结构设计

用于训练的数据采用与前一步骤中FCM不同的数据。首先需要确定当组训练数据在多维空间中的重心坐标，以及该重心坐标对应的1～3个沃罗诺伊中心点，即确定激活哪些沃罗诺伊子细胞，此后将用3种不同的优化算法对规则进行计算。

局部优化采用的算法是最小二乘法。每个沃罗诺伊子细胞被单独训练，并只采用此子细胞内的训练数据。计算公式为式(8)，在这种算法中c向量只包括一个子细胞中的所有规则。这种算法保证了每个子细胞内部的局部准确性。但由于沃罗诺伊子细胞之间有着空白区域，这部分没有被训练过的变量定义域会在结果中显示出不可预测的误差。

为了减小这种子细胞之间的跳跃式变化，以保证模型的连续性和在控制工程中的可控性，加权最小二乘法因其插值特性而有着更大的优势。训练数据的重心坐标将被作为式(10)中的权重向量，对当前被激活的沃罗诺伊子细胞中的规则作加权和，故此算法进行的是全局优化。由于每组训练数据激活的子细胞不同，在这种算法中将会对所有的子细胞同时进行优化。在具体算法上的表现为c向量将由所有子细胞的所有规则组成。作为非线性优化算法的代表，Levenberg-Marquardt方法成功与否的一个重要标准是起始值。为了保证起始值有一定的参考性，将使用局部优化法的规则结果作为起始值。

3 结果分析

对z=xysin(xy)函数、钟摆系统的建模和模拟结果进行分析，并对3种参数优化算法以及不同模糊变量的变量数目进行比较。

3.1z=xysin(xy)函数的结果分析

在1 000组检验数据基础上，对模型所得出的函数值和函数曲线进行分析。图6中所显示的是经过FCM计算出来的25个沃罗诺伊中心，而图7则显示了其对应的德劳内三角化结果。图8 — 图10则展示的是基于这25个中心，每个变量有3个不同值的建模误差分布。可见，非线性优化法有着不可比拟的优势，而另2种优化法的区别不十分明显，并在边缘区域有着较大误差。

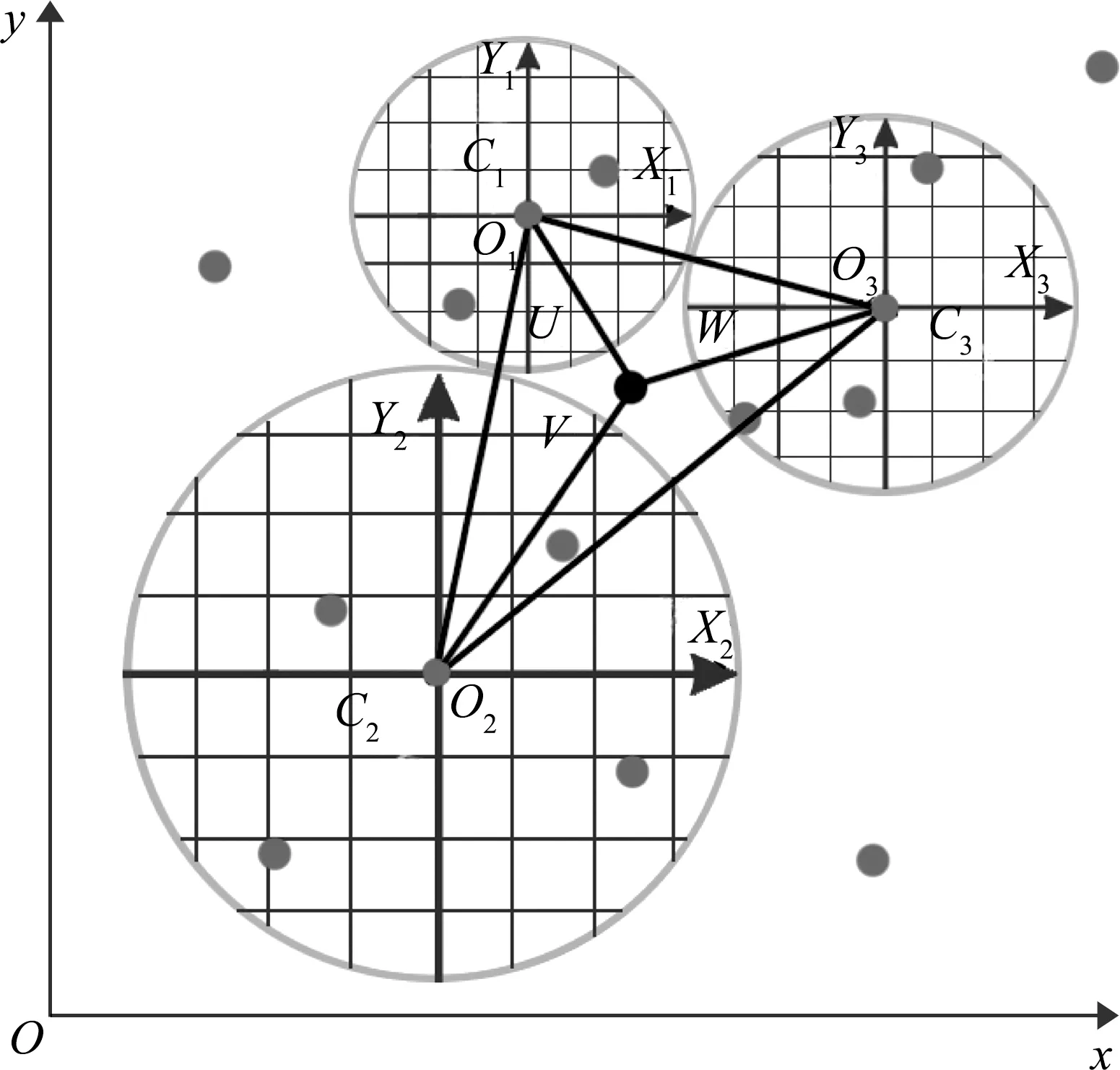
图6 FCM计算图示

图7 z=xysin(xy)的25个沃罗诺伊中心及德劳内三角化图

函数z=xysin(xy)的模糊逻辑模型在不同参数下的模拟误差与计算时间见表2。其中，归纳总结了不同的沃罗诺伊中心个数和不同变量数目对模型精度和计算时间的影响。从表2中也可以看出，非线性优化算法的精确度最高，但其计算时间也明显长于其他2种算法。加权最小二乘法则由于插值而损失了一部分精度，但由于此算法只需要进行一次逆矩阵运算，而普通最小二乘法则需要进行与沃罗诺伊子细胞数目相同次数的逆矩阵运算，故相比之下加权最小二乘法的运算成本更低。其另一个优势在于，由图11和图12的对比可以看出，系统的误差相比普通最小二乘法走向更为平缓，从而有着更好的函数连续性。

图8 z=xysin(xy)函数的最小二乘法建模误差

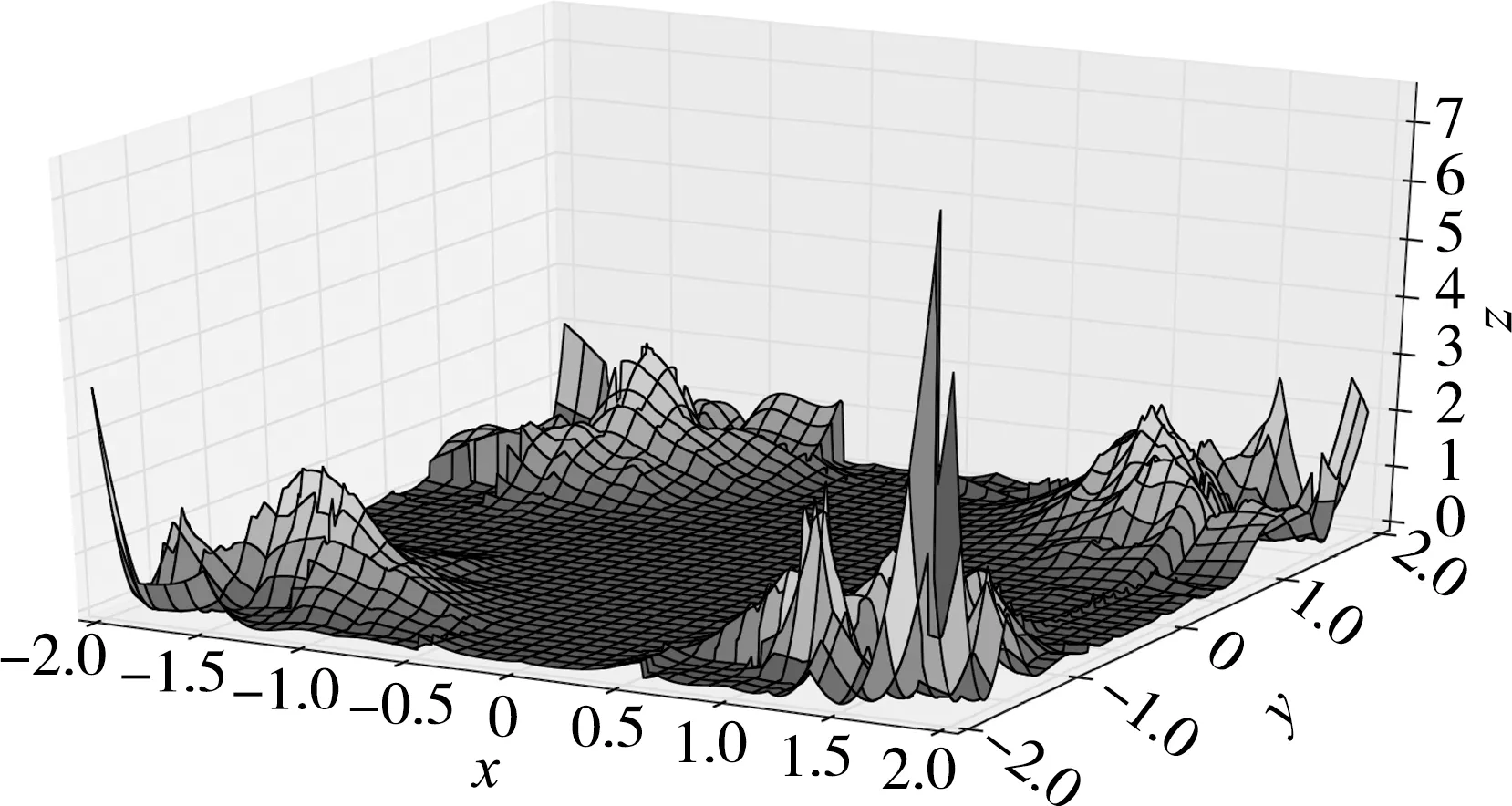
图9 z=xysin(xy)函数的加权最小二乘法建模误差

图10 z=xysin(xy)函数的非线性优化法建模误差

表2 z=xysin(xy)的模糊逻辑模型在不同参数下的模拟误差与运算时间

3.2 钟摆系统的结果分析

由于过高的维度，钟摆系统的模型将无法在此展示。因为在使用3个变量时，Levenberg-Marquardt方法在运行5 d后依然没有得到结果，我们统一对所有模拟试验采用了20个沃罗诺伊中心和2个变量，其计算结果见表3。

表3 钟摆模糊逻辑模型在不同算法下的模拟误差与运算时间

分析得知，在2个最小二乘法的误差中分别存在一个较大的离群值，而去掉这个离群值后，这2种算法的均方差也会降低到十分位到百分位的级数上。加权最小二乘法有着十分明显的运算时间短的优势。但是其缺陷在于，删除离群值的可行性在现实应用中也会受到很多限制。而较大的离群值不仅会对系统建模的方差有影响，还会使得模型的连续性变差，从而使得模型在某些范围内不可控。相比之下，Levenberg-Marquardt方法在可以接受的运算时间内，有着很高的模型仿真程度和稳定性。

4 结 语

通过对传统模糊逻辑系统进行结构优化和参数优化，用模糊逻辑系统对静态函数及动态系统进行了双层递归式的建模。这种结构的优势在于用较少的规则数目，对较为复杂的系统进行模拟。模型的测试结果显示，这种建模方式具有一定的可行性。加权最小二乘法运算时间短，而Levenberg-Marquardt方法所得的模型则十分精准。

在今后的研究中，需要对离群值的产生原因进行分析，从而减小或者消除系统的不连续性。对使用不同算法、不同参数的模型可在控制器上进行检验，以确定它们的可控性。此外，还可将此模型与同样规则数量的单层结构进行对比，从而对分层的优劣点进行验证。

[1] BABUSKA R.System Identification Using Fuzzy Models[J]. Control Systems,Robotics and Automation, 1991,6(1):28-30.

[2] ZHANG J, MORRIS J. Recurrent Neuro-fuzzy Networks for Nonlinear Process Modeling[J]. IEEE Transactions on Neural N,1999，10(2):313-326.

[3] CORDON O, HERRERA F, ZWIR I. Hierarchical Knowledge Bases for Fuzzy Rule-based Systems[J]. IEEE Transactions on Fuzzy,2000,9(1):310-313.

[4] 杨新宇,曾明,王军,等.一种基于模糊逻辑的被动测量自适应抽样算法[J].计算机工程,2004,30(9):21-22.

[5] 王士同.模糊系统、模糊神经网络及应用程序设计[M].上海：上海科学技术文献出版社，1980:4-48.

[6] ZADEH L A, KING-Sun Fu, KOKICHI T, et al. Fuzzy Sets and Their Applications to Cognitive and Decision Processes [C]. Academic Press Inc,1975: 329-352.

[7] 王永贵,李鸿绪,宋晓.MapReduce模型下的模糊C均值算法研究[J].计算机工程,2014,40(10):47-51.

[8] KAVKA C, SCHOENAUER M. Evolution of Voronoi-Based Fuzzy Controllers[J]. PPSN VIII, Lecture Notes in Computer Science, 2004(10):541-550.

[9] APPOLONI J, KAVKA C, ROGGERO P. Evolution of Recurrent Fuzzy Controllers[R].VI Workshop de Investigadores en Ciencias de la Computación,2004:601-606.

[10] HANSFORD F.Lineare Algebra: E in Geometrischer Zugang[M]. Berlin, Germany：Springer Verlag Berlin Heidelberg,2003:138-140.

[11] NEALEN A. An As-short-as-possible Introduction to the Least Squares, Weighted Least Squares and Moving Least Squares Methods for Scattered Data Approximation and Interpolation[R]. Group TU Darmstadt,2004:15-20.

[12] GAVIN H P. The Levenberg-marquardt Method for Nonlinear Least Squares Curve-fitting Problems[R]. Department of Civil and Environmental Engineering, Duke University,2013:63-70.

[13] YANG W Y, YONG S C, CHANG Y C, et al. Matlab/Simulink for Digital Signal Processing[J]. Signal Processing,2013，24(7):24-36.

Implementation of Hierarchical Recurrent Fuzzy Logical System Model

XULimou1LIChangyun2MANJunfeng2

(1.Department of Information Engineering, Zhongshan Torch Polytechnic, Zhongshan Guangdong 528437, China; 2.School of Computer and Communication, Hunan University of Technology, Zhuzhou Hunan 412007, China)

In order to solve the problems in traditional fuzzy logic system, three different hierarchical recurrent fuzzy logical systems are proposed based on the measured data system. Python language is used to verify the feasibility of the new structure. Under static and dynamic conditions, the proposed three structures have their own advantages and can be applied in different fields.

fuzzy logical system; dynamic system simulation; static function simulation; hierarchical structure

2017-01-05

国家科技部科技支撑计划项目“两型农村社区信息化管理应用技术集成”(2013BAJ10Bl4-5)

徐利谋(1981 — )，男，硕士，高级工程师，研究方向为计算机应用和物联网应用开发。

TP391.9

A

1673-1980(2017)03-0083-06