搅拌固液悬浮研究进展
杨锋苓,周慎杰
搅拌固液悬浮研究进展
杨锋苓1,2,周慎杰1,2
(1山东大学机械工程学院,山东济南250061;2高效洁净机械制造教育部重点实验室(山东大学),山东 济南250061)
固液悬浮是典型的单元操作,对其进行研究具有重要意义。回顾了60年来搅拌容器内固液悬浮的研究历程,介绍了常见的搅拌悬浮设备结构,对比分析了有挡板和无挡板时的临界悬浮转速,阐述了固液悬浮的各种实验测试及数值模拟方法,论述了自由液面变形对搅拌固液悬浮的影响及研究现状,并展望了未来在数值研究方面的发展方向。
搅拌容器;固液悬浮;多相流;自由液面;计算流体动力学
引 言
固液悬浮是借助搅拌桨的作用使固体颗粒悬浮在液体中以形成固液混合物或悬浮液的一种固液两相混合过程,对于某些操作,例如涉及气相反应物的催化反应等,还需要通气,此时即为气液固三相混合[1-6]。就液相而言,可为牛顿流体或非牛顿流体;就固相而言,根据其密度与液相密度之间的关系,可分为沉降颗粒和自浮颗粒[7-10],对于复杂的悬浮体系,还可能是多种固体颗粒的混合物[11-13]。固液悬浮研究的主要内容是如何形成并维持尽可能混匀分布的悬浮液以增强固液相间的传质效率[14]。迄今为止,除悬浮机理外,人们主要在两个方面就固液悬浮做了大量研究工作。一是临界悬浮转速、搅拌功耗、颗粒浓度及尺寸分布、颗粒停留时间分布和悬浮高度的实验测试、理论分析和数值研究;二是如何提高悬浮性能,即保证搅拌容器内的固体颗粒在一段时间内维持较高的分布均匀程度,并尽可能地降低功耗。为此,学者们就搅拌容器的结构参数和操作条件与悬浮性能之间的关系进行了系统地研究,同时分析了固相和液相性质的影响。其中结构参数主要包括搅拌桨类型、尺寸、数量、离底高度、安装位置(中心安装、偏心安装、侧入式安装、斜插式安装等)、泵送方向(主要指轴流桨,例如斜叶桨)、搅拌容器底部的形状和粗糙度、挡板数目及类型和安装形式、导流管结构、气体分布器类型及安装位置等,操作条件主要指搅拌桨转速、通气速率、气含量等,固相性质包括颗粒密度、颗粒形状、尺寸、固含量,液相性质则指液体密度和黏度[2,14-19]。此外,还有少量学者研究了固相的存在与液相宏观不稳定性之间的关系,分析了固含率对宏观不稳定频率的影响[20-22]。本文主要就搅拌悬浮设备结构、临界悬浮转速、固液悬浮研究方法进行综述;此外,就现有关于自由液面固液悬浮的研究现状进行概括,并指出未来的研究方向。
1 搅拌悬浮设备结构
搅拌容器结构及其附件对固液悬浮效果有重要影响,尤其是搅拌容器底部的形状以及搅拌容器内是否有挡板和导流管。有关固液悬浮的大多数研究针对的都是平底搅拌容器,搅拌桨大多是径流型Rushton桨和平叶搅拌桨以及轴流型斜叶桨、莱宁桨、螺旋式推进桨、翼型桨等,而且搅拌容器内通常安装挡板,也有一部分研究针对的是碟形底和曲面底搅拌容器。有关研究证明,平底容器和锥形容器容易产生粒子堆积,碟形容器可较好地解决堆积问题,但功耗较大,相比之下,曲面底搅拌容器可避免上述困难。此外,为避免形成液体回转区,搅拌容器内一般要安装挡板,有时还要安装导流筒, 以便使轴向速度分布更均匀。设置导流筒后,搅拌容器内一般不再需要设置挡板,而且相同功耗时能产生更大的循环流量,提高浓度分布均匀性[23-27]。
1.1 无挡板搅拌悬浮
搅拌容器内设置挡板能改善固液悬浮效果,但功耗也会增大。因此,在某些情况下,无挡板固液悬浮搅拌容器的应用也比较普遍,而且还具有一些特定的优点。例如在结晶反应器中,挡板的存在将增加与晶体表面的摩擦,抑制晶体的生长,在一定搅拌功率下,无挡板搅拌容器更利于液体与颗粒间的传质,而且此时中央气液旋涡的存在也利于颗粒的有效悬浮[28]。Freudig等[29]比较了六折叶45°向下泵送式斜叶桨有挡板和无挡板搅拌容器内颗粒的沉降特性,结果表明,无挡板搅拌容器更利于颗粒分散,并且达到相同的颗粒分散效果时,无挡板搅拌容器所需能量更低。Sbrizzai等[30]利用直接数值模拟和拉格朗日法研究了轴流桨无挡板搅拌容器中颗粒粒度对分散特性的影响,发现随着颗粒粒度的增加,颗粒的悬浮性能降低。Brujes等[31]分析了有挡板和无挡板搅拌容器内微胶囊的悬浮过程,对此时的临界悬浮转速进行了研究,发现无挡板时的临界悬浮转速比有挡板时小,且与颗粒直径无关。单贤根等[32-33]采用光学测量法和数值模拟方法对斜叶桨无挡板搅拌容器内颗粒的浓度分布进行了研究,考察了不同搅拌转速、搅拌桨离底高度对颗粒局部浓度分布的影响,分析了固体颗粒的浓度分布规律,两种方法所得结果基本一致。周宏宝等[34]也采用该方法测定了搅拌容器中水和石英砂两相体系在不同轴向位置处局部固含率随转速的变化情况,确定了固体颗粒临界离底悬浮转速和最小均匀悬浮转速。Li等[35]采用相同方法研究了无挡板低剪切六斜叶桨搅拌容器内固液两相和气液固三相的悬浮问题,成功地分析了操作条件对固体颗粒悬浮特性和搅拌功耗的影响。Tamburini等[36]采用激光照明法研究了无挡板Rushton桨搅拌容器内玻璃珠-水两相体系的悬浮过程,发现所研究的情况下,即便搅拌速度超过临界悬浮转速,搅拌容器内也达不到均匀悬浮状态,而是存在一个稳定的环形吸引子,固体颗粒主要在该吸引子内运动。Brucato等[37]对顶部有盖的无挡板Rushton桨搅拌容器内的固液悬浮过程进行了实验研究,分析了固相浓度、颗粒直径和密度对临界悬浮转速的影响,对比了有无挡板的情况下达到临界悬浮转速时的功耗,发现无挡板时的临界悬浮转速和功耗都比有挡板时小,但他们没有分析搅拌桨尺寸以及桨叶安装高度对临界悬浮转速的影响。该课题组在随后的研究工作中分析了这些因素以及颗粒尺寸和液体黏度的影响,给出了临界悬浮转速公式,进一步验证了无挡板悬浮的优越性[38]。最近,他们又分析了顶部无盖时无挡板搅拌的固液悬浮性能,指出可利用搅拌过程中产生的自由表面涡的吸附效应将气体吸入液体内部,实现气液固三相悬浮,克服了利用气体分布器供气时固体颗粒易堵塞通气孔的缺点,与有挡板时相比,还能降低功耗,但他们的研究仅限于小尺度的实验装置,没有进行放大实验,结果的工业应用可靠性还有待商榷[39]。来永斌等[40]也对无挡板搅拌容器内的固液悬浮进行了可视化研究,分析了搅拌桨离底高度、搅拌桨类型对颗粒的悬浮状态与临界悬浮转速及功耗的影响,但没有进行定量研究,结果可靠性尚需验证。杨锋苓等[41]对无挡板Rushton桨搅拌容器内石英砂-水固液悬浮过程的实验研究发现,无挡板时的临界悬浮转速和功率准数都比有挡板时小,且均随搅拌桨安装高度的增大而增大,随桨径比的增大而减小,=/5、=/3时的悬浮性能最好,增大桨径比和转速均不能明显改善固液悬浮效果。Wang等[42-44]的实验研究也表明,无挡板悬浮能显著降低功耗,相同功耗时无挡板悬浮的效果更好,而且与有挡板悬浮不同的是,无挡板时径流桨比轴流桨能效更高,节能效应更明显。他们后来的研究表明,造成无挡板悬浮时功耗降低的原因在于涡流效应,当Reynolds数大于500时,与相同功耗时的有挡板悬浮相比,涡流效应可增加槽体壁面附近流体的速度,降低沉降深度,即便对非牛顿流体也有效。然而,涡流效应仅在一定固含量范围内才比较明显,固相体积分数不超过0.2%时,径流桨可节能80%,混流桨和轴流桨可分别节能50%和40%[45-47]。
1.2“非传统”搅拌悬浮
通常情况下,搅拌桨都是中心安装,即搅拌轴与搅拌容器中心线重合,但也有其他安装形式下的固液悬浮。在一些特大型平底搅拌容器中,由于其具有搅拌桨直径相对较小、要求搅拌功耗较低、安装位置较特殊等特点,搅拌桨通常是侧入式安装。这一形式广泛应用于石化、食品、造纸等行业,脱硫吸收塔反应器内的固液悬浮就是典型的例子。Kipke[48]较早地研究了侧入式搅拌容器的固液悬浮性能,分析了搅拌轴的偏转角、桨径比及搅拌桨类型(EKATO推进桨、翼型桨和六斜叶桨)对悬浮性能和搅拌功耗的影响,发现搅拌轴的偏转角对固相浓度分布有重要影响,最佳偏转角时能实现均匀悬浮,小于最佳值时颗粒会堆积在搅拌容器底部和壁面连接处,大于最佳值时容器底部又会有大量颗粒堆积,并指出最佳值的确定与搅拌容器的尺寸有关。桨径比和桨型对功耗有影响,EKATO推进桨和翼型桨的功耗相当,六斜叶桨的功耗约为前两者的4倍;另外,对同一搅拌桨而言,桨径比大时功耗低,悬浮效率高。Chen等[49]建立了侧入式搅拌的数值模型和模拟方法,研究了3个侧入式桨搅拌容器内的固液悬浮,分析了转速、颗粒尺寸和固相体积分数(最高达15%)对临界悬浮转速、颗粒悬浮高度和悬浮均匀程度以及液相流场的影响,同时考察了湍流模型对模拟精度的影响。研究结果对侧入式搅拌的数值模拟提供了有效方法,遗憾的是没有分析搅拌桨布置形式对悬浮性能的影响。黄雄斌等[50-51]系统地分析了搅拌桨排列方式、离底高度、伸入长度、搅拌轴倾角、物性参数和液位高度对侧入式搅拌固液悬浮性能的影响,并量化了搅拌轴的水平偏转角对功耗的影响,其结果为工业设计提供了有益的参考依据。他们还指出侧入式搅拌存在密封问题,维修保养成本高。为此,针对高径比小于1(即搅拌容器的直径大于高度)的立式圆筒储罐,他们提出了多轴立式搅拌方式,不仅便于安装维护,而且多轴同时搅拌降低了单个搅拌桨对功率的要求,无须密封,成本远低于单轴立式和侧入式搅拌,在大型储罐中具有广阔的应用前景[52]。
此外,还有其他非传统搅拌悬浮形式,例如Yoshida等[53-54]研究了正反转式Rushton桨搅拌容器内的固液悬浮过程,发现该搅拌方式有助于抑制自由表面涡的形成,能改善搅拌容器底部的悬浮性能,且降低了功耗。车占富[55]研究了搅拌轴倾角和偏心率对单层斜插式四斜叶桨搅拌容器内固体悬浮特性的影响,发现斜插式搅拌比中心搅拌时的临界悬浮转速小,混合时间短,功耗低,并指出搅拌轴最佳倾角为17.5°,若偏心安装,则最优偏心率为0.1。杨锋苓等[56]采用数值模拟的方法对四斜叶桨偏心搅拌容器内的球形玻璃珠和水两相体系的固液悬浮进行了研究,分析了偏心率对流型、颗粒浓度分布及功耗的影响,指出偏心搅拌时浓度分布比中心搅拌时均匀,且具有节能功效;不同偏心率的改善效果不同,偏心率0.21左右时悬浮效果最理想,此时的临界悬浮转速约为中心搅拌时的80%,功耗约为中心搅拌时的90%。他们随后采用实验方法对Rushton桨偏心搅拌容器内石英砂-水两相体系的悬浮过程进行了研究,发现偏心搅拌时的临界悬浮转速和功耗均随偏心率的增大而增大,偏心率较小时的临界悬浮转速比中心搅拌时低,相同搅拌转速时偏心搅拌的功耗比中心搅拌时大;偏心搅拌时的固相浓度分布比中心搅拌均匀,偏心率为0.2时的悬浮效果最好,此时的临界悬浮转速约为中心搅拌时的80%,具有节能效应[57]。来永斌等[40]对比分析了中心和偏心搅拌容器的固液悬浮性能,他们采用了可视化实验研究方法,认为偏心搅拌时临界悬浮转速和功耗均比中心搅拌时大,且随偏心率的增加而增大,不适合高浓度固液体系的悬浮。Gicala[58]对椭圆底四斜叶桨搅拌容器内的悬浮过程进行了非稳态数值研究,固相体积分数为3.7%,粒径为12.5mm。他们分析了液相速度和固相浓度的分布情况,采用固相体积分数的相对偏差这一指标衡量了偏心搅拌的固液悬浮性能,发现在所研究的情况下,200 s后就能达到均匀悬浮状态。周坤[59]研究了CBY桨偏心搅拌容器内颗粒的悬浮特性,对于自浮颗粒,偏心率介于0~0.45时均匀下拉转速随偏心率增大而减小,偏心率介于0.46~0.6时随偏心率增大而增大;对于沉降颗粒,临界悬浮转速比中心全挡板时高,且随偏心率的增大先增大后减小,在偏心率为0.35时达到最大值,约为全挡板时的1.4倍。
2 临界悬浮转速
固液悬浮主要有3种状态,一是使固体颗粒完全悬浮起来,称为完全离底悬浮;二是使固体颗粒在搅拌容器内均匀悬浮,简称均匀悬浮;将漂浮在液面上的固体颗粒悬浮在液体中也是主要研究的悬浮状态之一。以上悬浮状态中,完全离底悬浮的研究最普遍,要达到完全离底悬浮状态,搅拌桨的转速必须超过临界悬浮转速。
固体颗粒的离底悬浮机理主要有两种,一种观点认为悬浮是由湍动旋涡控制的,导致搅拌容器底部颗粒悬浮的原因是具有一定尺度的小旋涡的扰动。假定与颗粒尺寸同一数量级的小旋涡作用于固体颗粒,并将能量传递给固体颗粒,当旋涡作用力克服了固体颗粒所受重力与浮力之差时,颗粒就会悬浮起来。另一种观点认为,搅拌容器底部的主体流动是导致颗粒悬浮的主要原因,流体流经固体颗粒时,固体颗粒处于边界层内,容器底部的边界层对颗粒施加垂直向上的力,当流速达到一定值时,向上的作用力与固体颗粒的重力相等,沉积在搅拌容器底部的固体颗粒就达到了离底悬浮状态[60]。张凤涛等[61]对高固含量搅拌容器内临界离底悬浮转速的数值研究指出,主体流动机理解释固体颗粒的临界离底悬浮更为准确,但结果尚需实验验证。
2.1 有挡板搅拌
迄今为止,研究人员对有挡板时的临界悬浮转速做了大量研究,得到诸多关系式,其中Zwietering公式应用最广泛。Zwietering[62]对二叶平桨、Rushton桨、推进桨等多种不同形式的搅拌桨进行了大量实验研究,分析了颗粒性质、操作条件、设备结构等因素的影响,在综合分析的基础上,以固体颗粒在搅拌容器底部堆积的时间不超过1~2 s为完全离底悬浮的判据,给出如下关系式

到目前为止,该关系式的使用仍然十分广泛,但有局限性。例如公式中的常数由搅拌桨类型、尺寸及安装位置所决定,Zwietering只给出了桨式、六直叶圆盘涡轮式、风标式和推进式搅拌桨的值,对于其他形式搅拌桨的值,需要通过对实验测得的数据曲线进行拟合来确定。此外,值还与桨径比有关,而与桨叶离底高度无关。Ayranci等[63]指出,Zwietering公式是在固相质量分数不超过2%的前提下得到的,对于高固含量情况,应用时有偏差。他们还给出了自己的临界悬浮转速公式,但经过分析发现,所提出的公式[见文献[63]的式(10)、式(11)]和Zwietering公式具有相同的形式,并未像他们所说的那样考虑搅拌桨离底高度的影响,不同之处在于分析了颗粒类型的影响,用3个不同的指数0.17、0.23和0.32代替Zwietering公式中的指数0.13,并指出通用值为0.23,适用的固相质量分数高达35%。Narayanan等[64]指出,Zwietering公式的预测值偏高,Brucato等[65-66]也发现,Zwietering公式对临界悬浮转速的预测值偏高,当转速达到预测值的80%时,槽内固体颗粒即可达到完全离底悬浮状态。
Narayanan等[64]对有挡板的8叶Paddle桨搅拌容器内的固液悬浮进行了理论和实验研究,他们从颗粒的受力平衡出发,理论推导了如下关系式

该理论推导假定固体颗粒完全被液体润湿,没有考虑固液两相间的滑移速度,其结果低于实验观测值,两者之间存在如下关系
js,E=js,T×1.98-0.22(3)
然而Narayanan公式同样存在缺陷,所研究的搅拌容器直径不超过141 mm,没有进行放大研究,而且仅限于Paddle桨这一种桨型,也没有考虑桨叶离底高度的影响(研究过程中固定为1/2)。
Baldi等[67]基于湍动旋涡悬浮机理,对有挡板的8叶Paddle桨搅拌容器内不同颗粒直径、密度、浓度和操作条件下的固液悬浮进行了大量实验研究后,得到如下悬浮公式

同样,该公式也没有考虑桨叶离底高度的影响。事实上,桨叶安装高度的变化影响搅拌容器内的流场,这势必会对固体颗粒的悬浮产生一定的作用。Nienow[68]通过实验发现,临界悬浮转速与桨叶安装高度有关,随桨叶安装高度的降低而减小,并给出了Rushton桨在1/7、1/5、1/3时临界悬浮转速的值与桨叶离底高度间的关系。Armenante等[69-70]量化了桨叶离底高度和桨叶直径对临界悬浮转速的影响,认为不同桨叶离底高度范围的临界悬浮转速是不一样的,并在Zwietering公式的基础上给出了修正的临界悬浮转速公式,据此求得的临界悬浮转速值与实验值吻合极好。对于Rushton桨,1/5时修正后的临界悬浮转速公式为
(5)
1/6时,修正后的临界悬浮转速公式为

=b+/2 (7)
式中,为桨叶宽度,对标准Rushton桨,=/5。
Molerus等[71-72]于1987年提出了又一临界悬浮转速计算式,他们对悬浮机理进行了研究,着重分析了颗粒直径对临界悬浮转速的影响,认为当颗粒直径较大时,临界悬浮转速由搅拌容器的泵送特性所决定;而当颗粒直径较小时,搅拌容器底部边界层内的流动状态是决定固液悬浮的重要因素,对于完全浸入黏性底层内的固体颗粒,只有当壁面剪切应力w超过临界值时才能悬浮起来,此时对应的搅拌转速即为临界悬浮转速。对给定的固液悬浮体系,壁面切应力取决于颗粒的直径和固液两相密度

壁面切应力又与壁面摩擦速度有关
(9)
壁面摩擦速度由式(10)确定

式中,为边界层外流体的时均速度
=p(11)
边界层厚度为
=*/(12)
式中,*为量纲1壁面距离,*=5对应于黏性底层的厚度。由式(8)~式(12)整理得壁面摩擦Reynolds数为

当0≤≤5时,固体颗粒完全浸入黏性底层。需要指出的是,当固相体积分数不超过30%,且搅拌容器直径不超过1.5 m时,上述公式求得的临界悬浮转速才有效,且与固相体积分数无关。
Armenante等[73]还对多层桨搅拌容器内的临界悬浮转速进行了研究,定量地分析了搅拌桨的类型和数目、搅拌桨直径和离底高度以及桨间距对临界悬浮转速和功耗的影响,并指出除非是工艺需求,一般不建议采用多层桨进行固液悬浮操作,因为多层桨不仅会增加临界悬浮转速,还会增加功耗。Kasat等[16]对单层和多层桨搅拌容器内临界悬浮转速的实验研究情况进行了综述,讨论了临界悬浮转速的测定方法,分析了搅拌桨的类型、结构、离底高度、数量以及固体颗粒的性质等因素对临界悬浮转速的影响,在总结前人研究结果的基础上,给出了今后的发展方向,同时指出应加强对多层桨固液悬浮的研究,尽管多层桨会增加功耗,但对于高径比较大的搅拌容器以及气液固三相悬浮体系而言,多层桨会提高固体分布的均匀程度,还有利于自浮颗粒的悬浮。
2.2 无挡板搅拌
近年来的研究表明,无挡板搅拌时的临界悬浮转速比有挡板时小[29,31,37-39],具有节能功效。然而,目前尚无通用的临界悬浮转速公式,只是针对特定的搅拌体系,一些学者给出了特定操作条件下的经验关系式。例如Pavlushenko等[74]对顶端无盖的翼型桨无挡板搅拌容器内不同固含量的石英砂及铁矿砂在多种不同黏度的液体中的悬浮特性进行了研究,给出了如下临界悬浮转速公式

Nagata[75]给出的顶端无盖时无挡板斜叶桨中心搅拌容器内的临界悬浮转速公式为
(15)
Yoshida等[53-54]发现正反转式Rushton桨的临界悬浮转速取决于离底高度,具体形式如下。
1/10

1/6
(17)
Tamburini等[38]对顶部有盖的无挡板Rushton桨搅拌容器内的固液悬浮进行实验研究时,得到了如下临界悬浮转速公式

3 固液悬浮实验研究
早期固液悬浮实验研究采用的是可视化观测法[62, 76-77],这种方法主观依赖性强,难以给出定量的结果。鉴于此,后期采用的都是基于固相浓度的定量测量法,可分为两大类:接触式和非接触式。
3.1 接触式测量
接触式测量方法主要包括取样法、电导法、测压法、光学探针法。取样法操作比较烦琐,取样浓度不能真实反映测量点处的浓度值,不易做到“等动力”取样,且取样管型式和取样条件对测量结果有很大影响,效率低、测量精度差[25,78-81]。电导法通过测量不导电的固体颗粒对悬浮体系电导性质的影响来确定颗粒的局部浓度,测量结果明显优于取样法,但实验中所用的液相的纯度、电导率及实验温度等条件的改变都会对体系的最终测量结果产生显著影响,此外,电导探针的型式也会影响测量结果[82-84]。测压法认为悬浮的颗粒越多,作用在搅拌容器壁面上的压力就越大,因此,可把压力计布置在搅拌容器四周,通过测量作用在搅拌容器壁面上的压力变化就能间接反映固体颗粒的悬浮浓度,而且对搅拌容器结构没有任何要求,也能用于工业搅拌容器内固液悬浮浓度的测量[85-87]。光学探针法的基本原理在于,固液悬浮体系中,稳定光源的光减弱程度与固相浓度、粒径、液体的投射性等因素有关,当光程及液体介质固定时,对于一定粒径的同种固体颗粒而言,影响测量光强度变化的影响就只有固相浓度,因此可通过测定透射光强度随固相浓度的变化关系来测量悬浮体系中的固相浓度[88]。光学探针法在固液悬浮浓度测量方面有广泛的运用,Yamazaki等[89]就采用该方法对搅拌容器内的固相浓度分布进行了测量,研究了不同固体颗粒的浓度分布情况,并利用所得实验数据建立了一种沉降-扩散模型。Angst等[90]也采用光学法对搅拌容器内的固相浓度分布进行了测量,他们使用的是直径为7 mm的内窥镜探头,将其置于悬浮体系中,以接收由固体颗粒反射回的光,反向散射的光强通过光纤传输到CCD相机内,然后利用IMAGEJ软件对得到的光强进行灰度分析来测量固相浓度,但其应用多限于颗粒粒径大于200 μm、且颗粒平均固含率大于1%的情况。随着精确测量技术的发展,目前已经开发出了针对固体颗粒浓度测量的新型光学测量仪器PC-6A粉体浓度测量仪,它可用于较高固相浓度的悬浮体系的测量,但探针直径有3 mm,对流场仍有一定的干扰[32-35]。
3.2 非接触式测量
接触式测量法不可避免地对被测量体系产生干扰,降低测量精度,因此非接触式测量方法就十分重要。激光散射法(light scattering technique, LST)就是一种非接触式测量方法,可用于高固含量固相浓度的测量,其原理是通过激光来照亮被测量的悬浮体系,对经过固体颗粒散射后的光强进行分析得到颗粒的浓度。该方法简便易行,但要求固相和液相对光的反射指数相当,否则只能用于固相体积分数不超过0.3%的悬浮体系;该方法还要求搅拌容器必须是透明的,限制了工业应用[91]。激光束图像分析法(light sheet image analysis, LSIA)采用激光束照明被测量的浓度场,采用高分辨率CCD相机对照亮的二维界面拍照,固体颗粒在获得的图片上显示为白色的亮点,利用Matlab对获得的大量图片进行后处理就可以得到固体颗粒的浓度分布情况,但只能用于低固含量固液悬浮体系的测量[36,92]。光束衰减法(optical attenuation technique, OAT)以二极管激光器为光源,硅光电二极管为接收器,光束水平照射搅拌容器内的悬浮体系,固相的存在导致光强的衰减,通过标定即可得到光强与固相浓度之间的对应关系。对不同高度平面内的光强进行测量,就能获得固相浓度的轴向分布[93]。
以上3种方法都要求搅拌容器必须是透明的,应用范围有限。相比之下,以下方法具有明显优势。例如电阻成像法(electrical resistance tomography, ERT),该测试系统的核心部件是由铂、金、银、铜等贵重金属或者银钯合金制成的电极,测试过程中将一系列电极均匀布置在搅拌容器壁面并与数据获取系统相连,电极通过与容器内的流体接触测得电场分布情况,然后由图像重建系统获得电阻分布[94]。该方法对搅拌容器是否透明没有要求,适用于工业设备内颗粒浓度的测量,已广泛应用于过滤、聚合、旋流分离以及混合等多种化工过程。例如Hui等[95]采用ERT方法成功地测量了侧入式Maxflo桨搅拌容器内纸浆纤维在悬浮过程中于搅拌桨附近区域内所形成的假塑性流体洞穴的体积随转速的变化情况, Sardeshpande等[96]采用ERT方法测量了无挡板搅拌容器内固体颗粒对液相混合时间的影响,Carletti等[97]采用ERT方法研究了六斜叶桨有挡板搅拌容器内球形玻璃珠在饱和氯化钠水溶液中的悬浮过程和液相混合时间。此外,计算机自动辐射颗粒追踪法(computer automated radioactive particle tracking, CARPT)和正电子发射粒子追踪法(positron emission particle tracking, PEPT)的应用也较为普遍。CARPT法在搅拌容器内加入与悬浮的固体颗粒具有相同尺寸和密度的辐射性粒子,该粒子随悬浮颗粒一起运动,通过在搅拌容器外布置的一系列探针来测量粒子的辐射强度,进而反映悬浮颗粒的局部浓度。该方法需要事先标定,在搅拌容器内指定位置处放置辐射粒子,检测它的辐射强度,通过对多个位置处辐射强度的测量得到粒子位置与辐射强度间的关系[66,98-99]。PEPT法利用一种放射性正电子同位素作为示踪粒子,正电子从原子核中释放后会与电子中和形成g射线,利用探测器对g射线进行跟踪就能得到示踪粒子的运动轨迹。该方法可用于高固含量的悬浮浓度测量[100-106],例如Liu等[106]就利用PEPT方法测量了六斜叶桨有挡板搅拌容器内球形玻璃珠在氯化钠水溶液中的悬浮,所用玻璃珠有5种不同的尺寸,固相体积分数最高达23.6%,成功地分析了液相速度和固相浓度分布情况。但PEPT设备昂贵,而且数据后处理比较麻烦,鉴于此王靖岱等[107-110]提出了声发射监测技术,悬浮液与器壁碰撞时会产生不同频率的声波信号,信号的频率取决于悬浮液的特性,可由固定在容器外壁面上的传感器接收,结合声信号的频谱分析、小波分解和R/S分析、Hilbert-Huang变换(HHT)等方法,对接收到的不同特征信号频段内的声波进行处理,即可获得声波能量随悬浮液浓度、搅拌转速的变化关系,以及沿搅拌容器轴向的变化规律,从而得到悬浮液的浓度分布、颗粒悬浮高度和临界悬浮转速。对于固含量不超过0.2%的固液悬浮体系,还可采用粒子图像测速技术(particle image velocimetry, PIV)[104,111-112]和激光多普勒测速技术(laser Doppler velocimetry, LDV)[113]进行测量。还有文献报道了超声多普勒测速技术(ultrasound Doppler velocimetry, UDV)[95,114-115]和超声波测速技术(ultrasound velocity profiler, UVP)[116]。UDV和UVP原理相同,利用超声波脉冲和多普勒频移技术测量固相速度。超声波脉冲以一定的频率(通常为4 MHz) 由传感器探针发射出去,在液体内部传播过程中遇到颗粒后部分能量被反射回来,并被传感器探针接收,接收到的反射波的频率由颗粒运动速度决定,通过发射波与接收波的时间延迟和频率变化就能计算出颗粒运动速度。然而,同PIV和LDV一样,UDV和UVP都不能测量固相浓度,只能测量速度。
4 固液悬浮数值研究
4.1 多相流模型
受测量方法和实验条件的限制,采用实验方法很难实现整个搅拌容器内固相浓度的测量,即便能测量成本也较高。因此采用计算流体动力学(computational fluid dynamics, CFD)方法对搅拌容器内的固相浓度分布进行研究就十分重要。
早期对固液悬浮的数值研究仅考虑固液两相间的单向耦合,不考虑固相的存在对液相的影响,仅计算液相流场,然后通过在每一个控制体积上求解质量平衡方程来计算固相的浓度,该类方法中运用较多的是沉降扩散模型[23,25,117-120]和沉降速度模型[121]。当固含量较高时,固相对液相的影响就不能忽略,因此该类方法仅能用于低固含量(≤5%)时固液悬浮的模拟,对于高固含量的固液悬浮模拟,必须考虑固液两相间的相互作用;与此同时,即便是固含量不高时,为了精确地模拟固液悬浮情况,固液两相间的耦合也不能忽略。此时可采用格子Boltzmann法(lattice-Boltzmann method, LBM),然而该方法计算量巨大,只能用于小尺度搅拌容器内低固含量的模拟,迄今为止,只有少量文献[13,122-123]报道了该方法在搅拌固液悬浮方面的应用。某些特殊情况下,悬浮颗粒的尺寸与搅拌容器的特征尺度相当,或者固含量较高,此时颗粒不能再被处理为稀疏相,而应该“单独看待”,模拟每一个颗粒周围流体的流动情况,这类问题可使用光滑粒子动力学(smoothed particle hydrodynamics, SPH)方法求解。例如,Prakash等[124]采用SPH方法模拟了搅拌容器内高固含量圆柱形木块的悬浮过程,成功地模拟了颗粒悬浮状态与搅拌桨转速之间的关系。
事实上,大多数涉及固液悬浮的工业过程中悬浮颗粒的浓度都不高,固相可被看作是稀疏的,可用拉格朗日法或欧拉法模拟。拉格朗日法将流体相视为连续相,在每一个控制体积上求解N-S(Navier-Stokes)方程;固体相视为离散相,随连续相一起运动,而且和连续相之间存在动量、质量和能量的交换。采用拉格朗日法计算流场和离散相的运动轨迹,便于正确地考虑颗粒与流场之间以及颗粒与壁面、颗粒与颗粒之间的相互作用力,能提供更为详细的有关颗粒运动轨迹的信息,但是它也需要大量的计算机内存和计算时间,当固含量较高时,需求就更大,因而只能用于固含量不超过的固液悬浮模拟[13,66,100,125-131]。然而,在工业固液悬浮过程中,固含量通常高于10%,Lagrange法不再适用,应采用Euler法。
在Euler法中,固相和液相被处理成互相贯穿的连续介质,即每一相占据的体积无法再被其他相占有,因此引进相体积分数这一概念,它是时间和空间的函数,所有相的体积分数之和等于1。另外,每一相都具有类似形式的守恒方程,可采用同样的离散形式进行求解。相对于Lagrange法而言,Euler法计算量小,在高固含量固液悬浮体系模拟中有广泛应用[132-140],适用于模拟工程实际问题。实际应用时可用稳态的多重参考系法或非稳态的滑移网格法模拟搅拌桨的旋转。通常情况下,滑移网格法计算量大,但能获得比多重参考系法更准确的结果[141];有时这两种方法获得的结果比较接近,此时可采用计算量小的多重参考系法[142]。此外,还应注意选择合适的相间作用力模型和湍流模型,以确保模拟结果的精度。常见的相间作用力包括曳力、升力、附加质量力、basset力、湍流扩散力等,但以湍流扩散力和曳力为主,其他相间作用力的影响可以忽略[17,37,133-134,143-144]。
固液悬浮数值模型还有另外一种分类方法,Blais等[86-87]将其分为3大类:微观-微观、介观-介观、介观-微观。微观-微观模型即Lagrange法,流体的解析尺度小于颗粒尺度,颗粒之间的相互碰撞采用离散单元法(discrete element method, DEM) 进行处理,但仅能模拟少量颗粒的运动。介观-介观模型就是通常所说的欧拉两流体模型,液相和固相被处理为相互贯穿的连续体。介观-微观模型即Euler-Lagrange法,以非解析的CFD-DEM模型为代表[87,145-147],流体的解析尺度大于颗粒,通过体均N-S方程(volume-averaged Navier-Stokes equations, VANS)求解,颗粒的运动及其相互作用通过DEM法求解,固液两相间的相互作用通过曳力、升力等来体现。尽管非解析的CFD-DEM模型对流体的解析尺度大,但能精确地模拟大量颗粒(数目高达107~108)的动力学性能[148-149],具有广阔的应用空间。
4.2 湍流扩散力模型
湍流扩散力模型描述了湍流脉动对固液两相间动量传递的影响,当颗粒尺寸小于湍动涡的尺寸时该力尤为重要[135],考虑它的影响时可以更好地预测固相浓度分布和颗粒悬浮高度[150]。常见的湍流扩散力模型有Lopez-de-Bertodano模型[151]、Simonin-Viollet模型[152]和Burns模型[153],应用最广泛的是Lopez-de-Bertodano模型

式中,TD为湍流扩散系数,推荐取值范围0.1~1.0。文献中常用值为0.1[139-140],ANSYS Fluent 16.1中的默认值为1.0。
4.3 相间曳力模型
常见曳力模型有Schiller-Naumann模型[154]、Morsi-Alexander模型[155]、Grace模型[156]、Ishii-Zuber模型[157]、Gibilaro模型[158]、Gidaspow模型[159]、Brucato模型[160]、Huilin-Gidaspow模型[161]等。现有研究表明,对搅拌固液悬浮模拟而言,Brucato模型和Gidaspow模型较为有效[17,162-164]。
Brucato模型考虑了湍流对颗粒的影响,主要用于模拟固含量不超过5%的固液两相及气液固三相悬浮,该模型中曳力系数的表达式为

(21)
s是相对Reynolds数

Brucato模型的缺点在于涉及湍动能耗散率的计算。众所周知,雷诺时均湍流模型对湍动能耗散率的模拟精度过低,大涡模拟和直接数值模拟可提高模拟精度,但计算量大,无法用于工程实际问题。
相比之下,Gidaspow模型更受欢迎,它考虑了颗粒之间的相互作用,是Wen-Yu模型[165]和Ergun模型[166]的组合。该模型中,相间曳力随固含量的增加而增大,固含量低于20%时,使用Wen-Yu模型模拟相间传质

其中曳力系数的表达式为
(24)
固含量高于20%时,使用Ergun模型
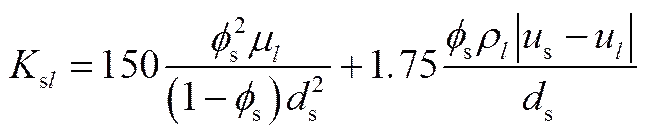
另外,Huilin-Gidaspow模型[161]对Gidaspow模型进行了改进,通过转换函数来实现从Wen-Yu模型到Ergun模型的自然转换
(26)
该模型的相间传质系数为

Tamburini等[137,163]也对由Wen-Yu模型到Ergun模型的过渡进行了处理,提出了一种线性插值方式。
如果悬浮物为多种不同颗粒组成的混合物,则曳力模型必须考虑不同种类颗粒之间的相互作用。文献中有相关报道,例如Montante等[11]模拟了有挡板的多层4叶圆盘涡轮桨搅拌容器内低固含量的固相混合物的悬浮,并进行了实验验证。组成固相混合物的颗粒具有相同的直径,但密度不同。鉴于固含量较低(1.5~3.6 g·L-1),模拟时仅考虑了液相对固相的单向耦合,并忽略了湍流扩散力对颗粒的影响,使用的曳力模型如下

式中,s1和s2为两种不同的颗粒在湍流流体中的沉降速度,与颗粒在静止流体中的最终沉降速度t之间有如下关系[167]
(29)
基于以上假设,他们发现对于由两种颗粒组成的稀疏固相混合物的悬浮而言,不同密度颗粒之间的相互作用可以忽略。
Ayranci等[12]实验研究了由5种不同颗粒两两组合所形成的高固含量的固相混合物的悬浮,分析了颗粒尺寸比和密度比对临界悬浮转速的影响,发现固相颗粒间存在强烈的相互作用,并导致临界悬浮转速的降低。随后,他们使用LBM和大涡模拟(large eddy simulation, LES)方法对玻璃珠和黄铜颗粒组成的混合物在水中的悬浮进行了模拟研究,结果发现尽管混合物的固含量最高只有1%,但颗粒之间仍存在明显的相互碰撞,对悬浮过程产生重要的影响[13]。
4.4 湍流模型
采用数值方法研究固液悬浮时,对湍流流场的研究也十分重要,就目前的研究情况来看,对固液悬浮搅拌容器内流场的模拟采用较多的还是雷诺时均(Reynolds averaged Navier-Stokes, RANS)模型,包括标准-模型、realizable-模型、RNG-模型、-模型、剪应力传输模型(shear stress transport model, SST)、雷诺应力模型(Reynolds stress model, RSM)等。相关研究表明,除了RSM模型外,其他RANS模型的模拟结果基本一致,但RSM模型涉及湍流的各向异性,尽管能给出较为准确的模拟结果,尤其是在搅拌容器顶部流域内,但计算量偏大,通常情况下使用的是各种不同类型的两相-模型[164,168],对搅拌桨运动的模拟采用的是稳态的多重参考系法,相关研究证明该组合方法能取得与实验比较吻合的结果[137-138]。具体而言,两相-模型按照复杂程度由低到高可分为均质、分段、扩散、非对称4种。与直觉相反的是,具有简单形式的两相均质-模型比其他3个模型的模拟精度高,但缺点在于它对悬浮物沉积高度的模拟值偏高[163,169],而且不能捕捉湍流的瞬态特性[17]。另外,Feng等[170]开发了两相显式代数应力模型(explicit algebraic stress model, EASM),发现其精度优于标准-模型,然而不能用于模拟高固含量的搅拌固液悬浮体系。
LES 模型在搅拌固液悬浮方面的应用研究也有报道,不过都是低固含量的悬浮体系[13,127,136,171]。例如Derksen等[127,136]采用LES模型和Lagrange法研究了Rushton桨搅拌容器内球形玻璃珠与水两相体系的悬浮,取得了与实验相吻合的结果,但最高固含量仅为3.6%。后来,他们又将LES 模型与Euler法相结合来研究搅拌容器内的固液悬浮,固含量仅为1%,通过与CARPT实验结果的比较他们指出,当固含量较低时,该组合方法能很好地预测固液悬浮搅拌容器内流场和湍动能分布情况。还有少量学者将直接数值模拟(direct numerical simulation, DNS)用于搅拌固液悬浮研究[30,122,172]。关于湍流模型在搅拌固液悬浮研究的应用情况有相关文献[16,20,130,163-164]给出了具体论述。概括地讲,LES模型和DNS模型比RANS模型能提供更为真实的模拟结果,但计算量大,仅限于低固含量、低Reynolds数、小尺度的固液悬浮体系,以后可考虑使用模拟精度高且计算量小的多尺度湍流模型,例如分离涡模型(detached eddy simulation, DES)、尺度自适应模型(scale-adaptive simulation, SAS)。但是同LES和DNS模型一样,DES和SAS模型都不能与欧拉多相流模型同时使用,仅能与RANS模型相配合。
值得注意的是,尽管大多数固液悬浮都发生在湍流状态下,但制药、食品等过程工业中有时还涉及层流和过渡流状态下的固液悬浮。目前对非湍流状态下的临界悬浮转速、固体颗粒间的相互作用、流型对颗粒浓度分布的影响规律等的认识尚不清晰,相关研究报道极少。就作者所知,只有Lassaigne等[86-87]先后对层流和过渡流状态下无挡板平底搅拌容器内的固液悬浮进行了实验和数值研究,搅拌容器直径=365 mm,搅拌机为斜叶桨,直径=/3,离底高度=/4,悬浮体系是固含量为6%~25%的球形玻璃珠和黏度为1~4 Pa·s的葡萄糖水溶液,搅拌桨转速最高达到800 r·min-1,<350。实验研究时采用的是测压法,数值研究时所用模型为自行开发的适用于高黏度液体的非解析的CFD-DEM模型。数值模拟结果与实验结果吻合较好,成功预测了颗粒的临界悬浮转速、固相浓度分布和液相流型。
5 自由液面固液悬浮
一般地,进行固液悬浮模拟时均不考虑自由液面变形,对于有挡板的搅拌容器而言,由于自由表面涡得到了抑制,这种处理方法是妥当的。然而如前所述,固液悬浮也可在无挡板搅拌容器和偏心搅拌容器内进行,此时自由表面涡的形成是不可避免的,为了获得准确的模拟结果,必须予以考虑。Švec等[173]还指出,自由液面悬浮在工业过程和自然界中占有非常重要的地位,他们基于LBM方法开发了能用于模拟非牛顿流体中刚性颗粒自由液面悬浮的数值模型,可有效地模拟数以万计的刚性颗粒的悬浮过程,但仅限于稀疏固相。
迄今为止,仅有极少搅拌固液悬浮方面的文献提及了自由液面变形[9,124,174-176],且其中又只有极少文献研究了液面变形情况。例如Prakash等[124]采用SPH方法模拟了圆柱形木块在水中的悬浮,木块相对密度为0.5,初始时悬浮在液面处;木块具有两种不同的尺寸,直径和高度分别为16 mm×22.5 mm和25 mm×35 mm,前者加载量为1.5 kg和4 kg,后者为1.5 kg。搅拌容器直径和液位高度均为1 m,搅拌桨为四叶翼型桨,直径=0.4,离底高度=/3。当转速超过180 r·min-1时,数值模型成功地捕捉到了自由液面的变化情况,可是在实际工业生产过程中,悬浮颗粒的尺寸要小得多,SPH方法不再适用。Özcan-Taşkin等[175]在研究桨径比对自浮颗粒悬浮特性的影响时,使用了滑移壁面模型和VOF(volume of fluid)模型模拟自由液面变形。搅拌容器直径=610 mm,搅拌桨为45°倾角的四斜叶桨和海伍德泰勒公司研发的三叶LE-20桨。通过与LDA(laser Doppler anemometry)实验结果的对比发现,当桨径比为=/2时滑移壁面模型和VOF模型得到的结果基本相同;而桨径比=/3时,VOF模型的结果更准确,但计算量也大。Nogueira等[176]模拟了悬浮聚合反应器内的自由液面变形,使用的是RNG-模型和PHOENICS软件中的相间滑移算法模型(inter-phase-slip algorithm model, IPSA),然而他们只模拟了气液两相流场,没有考虑固相的存在,因而不是真实的固液悬浮模拟。
6 结 语
过去60年来,搅拌固液悬浮的研究取得了巨大进展,研究人员开发了各种不同的实验测试方法和数值模型,对湍流状态下有挡板搅拌容器内的固液悬浮及气液固悬浮进行了系统研究,获得了大量有益的结论,为工业生产提供了有力的指导依据。然而,绝大多数研究针对的都是有挡板的搅拌容器,搅拌桨中心安装。近年来,随着其他搅拌形式的出现,例如无挡板中心搅拌、斜插式搅拌、偏心搅拌、往复式搅拌、侧入式搅拌等,使得人们有必要在现有基础上进一步澄清这些形式下的固液悬浮机理,解决这些搅拌固液悬浮形式中出现的新问题,例如气液固三相自由液面变形的模拟及变形对悬浮性能的影响规律。鉴于实验方法的局限性(接触式测量方法对实验结果有干扰,非接触式测量精度高,但设备较昂贵,且只能用于小尺度的实验模型),开发模拟精度高、计算量小且易收敛的多相搅拌固液悬浮数值模型,模拟悬浮过程中的自由液面变形势在必行。尽管多流体VOF模型和欧拉多相流模型可组合使用来模拟液面变形,但只能与RANS模型配合使用,限制了模拟精度,而且难以收敛。所开发的模型最好能与高级的湍流模型配合使用,才能对搅拌固液悬浮进行客观真实的模拟。
符 号 说 明

B——固相质量分数,% C——桨叶离槽底高度,m Cb——桨叶底部离槽底高度,m CD——湍流曳力系数 CDo——静止流体曳力系数 CTD——湍流扩散系数 D——搅拌桨直径,m ds——颗粒直径,m e——偏心率 Fdf——曳力,Pa FTD——湍流扩散力,Pa g——重力加速度,m·s-2 H——悬浮液的静压头,m K,K′——比例常数 Ksl——相间传质系数 k——湍动能,m2·s-2 N——搅拌桨转速,s-1 Njs——临界悬浮转速,s-1 Np——功率准数 Re——Reynolds数 Res——相对Reynolds数 Ret——壁面摩擦Reynolds数 S——Zwietering公式常数 T——搅拌容器直径,m u——时均速度,m·s-1 us——湍流流体中颗粒沉降速度,m·s-1 ut——静止流体中颗粒沉降速度,m·s-1 ut——壁面摩擦速度,m·s-1 Vs——颗粒的真实体积,m3 V′s——颗粒的视在体积,m3 w——搅拌桨叶宽度,m y——边界层厚度,m y*——壁面距离 e——湍动能耗散率,m2·s-3 l——柯尔莫哥洛夫长度,m m——动力黏度,Pa·s n——运动黏度,m2·s-1 r——密度,kg·m-3 t——切应力,Pa f——体积分数,% y——转换函数 下角标 E——实验 l——液相 s——固相 T——理论 W——壁面
References
[1] MICALE G, CARRARA V, GRISAFI F,. Solids suspension in three-phase stirred tanks[J]. Chem. Eng. Res. Des., 2000, 78(3): 319-326.
[2] NIENOW A W, BUJALSKI W. Recent studies on agitated three-phase (gas-solid-liquid) systems in the turbulent regime[J]. Chem. Eng. Res. Des., 2002, 80(8): 832-838.
[3] LI W B, GENG X Y, BAO Y Y,Micromixing characteristics in a gas-liquid-solid stirred tank with settling particles[J]. Chin. J. Chem. Eng., 2015, 23(3): 461-470.
[4] ZU L Z, ZHOU H B, YANG S F,. Configuration optimization and mass transfer in a dual-impeller bioreactor[J]. J. Chem. Eng. Jpn., 2015, 48(5): 360-366.
[5] YANG S F, LI X Y, YANG C,. Computational fluid dynamics simulation and experimental measurement of gas and solid holdup distributions in a gas-liquid-solid stirred reactor[J]. Ind. Eng. Chem. Res., 2016, 55(12): 3276-3286.
[6] DAVOODY M, RAMAN A A A, PARTHASARATHY R. Agitation energy efficiency in gas-solid-liquid stirred vessels operating at ultra-high solids concentrations[J]. Chem. Eng. Res. Des., 2016, 111: 34-48.
[7] BAO Y Y, HAO Z G, GAO Z M,. Suspension of buoyant particles in a three phase stirred tank[J]. Chem. Eng. Sci., 2005, 60(8): 2283-2292.
[8] 包雨云, 龙建刚, 高正明, 等. 上浮颗粒特性对三相搅拌槽内固-液悬浮及气-液分散的影响[J]. 高校化学工程学报, 2006, 20(1): 25-30. BAO Y Y, LONG J G, GAO Z M,. Effects of buoyant particle characteristics on solid-liquid suspension and gas-liquid dispersion in a three phase stirred tank[J]. Journal of Chemical Engineering of Chinese Universities, 2006, 20(1): 25-30.
[9] KHAZAM O, KRESTA S M. Mechanisms of solids drawdown in stirred tanks[J]. Can. J. Chem. Eng., 2008, 86(4): 622-634.
[10] 李良超, 徐斌, 杨军. 基于计算流体力学模拟的下沉与上浮颗粒在搅拌槽内的固液悬浮特性[J]. 机械工程学报, 2014, 50(12): 185-191. LI L C, XU B, YANG J. Sinking/floating particles solid suspension characteristics in stirred tank based on CFD simulation[J]. Journal of Mechanical Engineering, 2014, 50(12): 185-191.
[11] MONTANTE G, MAGELLI F. Mixed solids distribution in stirred vessels: experiments and computational fluid dynamics simulations[J]. Ind. Eng. Chem. Res., 2007, 46(9): 2885-2891.
[12] AYRANCI I, KRESTA S M. Design rules for suspending concentrated mixtures of solids in stirred tanks[J]. Chem. Eng. Res. Des., 2011, 89(10): 1961-1971.
[13] AYRANCI I, KRESTA S M, DERKSEN J J. Experiments and simulations on bidisperse solids suspension in a mixing tank[J]. Chem. Eng. Technol., 2013, 36(11): 1957-1967.
[14] PAUL E L, ATIEMO-OBENG V A, KRESTA S M. Handbook of Industrial Mixing: Science and Practice[M]. Hoboken, New Jersey: John Wiley & Sons, Inc., 2004: 543-584.
[15] OCHIENG A, ONYANGO M S. CFD simulation of solids suspension in stirred tanks: review[J]. Hem. Ind., 2010, 64(5): 365-374.
[16] KASAT G R, PANDIT A B. Review on mixing characteristics in solid-liquid and solid-liquid-gas reactor vessels[J]. Can. J. Chem. Eng., 2005, 83(4): 618-643.
[17] SHAH R E, SHAH R S, SAJJADI B,. Solid-liquid mixing analysis in stirred vessels[J]. Rev. Chem. Eng., 2015, 31(2): 119-148.
[18] JAFARI R, CHAOUKI J, TANGUY P A. A comprehensive review of just suspended speed in liquid-solid and gas-liquid-solid stirred tank reactors[J]. Int. J. Chem. Reactor Eng., 2012, 10(1): 1-32.
[19] SHAMLOU P A. Processing of Solid-Liquid Suspensions[M]. Boston UK: Butterworth-Heinemann Ltd., 2016.
[20] JAHODA M, MACHOŇ V, VLACH L,. Macro-instabilities of a suspension in an axially agitated mixing tank[J]. Acta Polytech., 2002, 42(3): 3-7.
[21] ENG M, RASMUSON A. Influence of solids on macro-instabilities in a stirred tank[J]. Chem. Eng. Res. Des., 2012, 90(8): 1052-1062.
[22] ENG M, RASMUSON A. Large eddy simulation of the influence of solids on macro instability frequency in a stirred tank[J]. Chem. Eng. J., 2015, 259: 900-910.
[23] NIENOW A W, MILES D. The effect of impeller/tank, configurations on fluid-particle mass transfer[J]. Chem. Eng. J., 1978, 15(1): 13-24.
[24] YAMAZAKI H, TOJO K, MIYANAMI K. Concentration profiles of solid suspended in a stirred tank[J]. Powder Technol., 1986, 48(3): 205-216.
[25] BARRESI A, BALDI G. Solid dispersion in an agitated vessel: effect of particle shape and density[J]. Chem. Eng. Sci., 1987, 42(12): 2949-2956.
[26] 肖建军,包雨云,黄雄斌,等. 带导流筒搅拌槽中循环流量的实验研究[J]. 华北工学院学报, 2003, 23(1): 25-29. XIAO J J, BAO Y Y, HUANG X B,. Experimental study on circulating flux in a stirred tank with draft-tube[J]. Journal of North China Insitute of Technology, 2003, 23(1): 25-29.
[27] 陈文民, 黄雄斌, 高正明. 固-液导流筒搅拌槽内流体流动和颗粒悬浮特性[J]. 过程工程学报, 2007, 7(1): 14-18. CHEN W M, HUANG X B, GAO Z M. Characteristics of fluid flow and particle suspension in a solid-liquid draft-tube stirred tank[J]. The Chinese Journal of Process Engineering, 2007, 7(1): 14-18.
[28] GRISAFI F, BRUCATO A, RIZZUTI L. Solid-liquid mass transfer coefficients in mixing tanks: influence of side wall roughness[C]//Institution of Chemical Engineers Symposium Series. Hemsphere Publishing Corporation, 1994, 136: 571-578.
[29] FREUDIG B, HOGEKAMP S, SCHUBERT H. Dispersion of powers in liquids in a stirred vessel[J]. Chem. Eng. Process., 1999, 38(4/5/6): 525-532.
[30] SBRIZZAI F, LAVEZZO V, VERZICCO R,. Direct numerical simulation of turbulent particle dispersion in an unbaffled stirred-tank reactor[J]. Chem. Eng. Sci., 2006, 61(9): 2843-2851.
[31] BRUJES L, LEGRAND J, CARNELLE G. Complete suspension of microcapsules in baffled and unbaffled stirred tanks[J]. Chem. Eng. Technol., 1998, 21(9): 735-744.
[32] 单贤根, 禹耕之, 杨超, 等. 无挡板搅拌槽中液-固体系的分散特性[J]. 过程工程学报, 2008, 8(1): 1-7. SHAN X G, YU G Z, YANG C,. Dispersion characteristics of solid-liquid suspension in an unbaffled stirred tank[J]. The Chinese Journal of Process Engineering, 2008, 8(1): 1-7.
[33] SHAN X G, YU G Z, YANG C,. Numerical simulation of liquid-solid flow in an unbaffled stirred tank with a pitched-blade turbine downflow[J]. Ind. Eng. Chem. Res., 2008, 47(9): 2926-2940.
[34] 周宏宝, 李向阳, 杨超, 等. 基于LED光源反射的液固搅拌槽中颗粒悬浮特性测定的光纤法[J]. 过程工程学报, 2011, 11(6): 933-937. ZHOU H B, LI X Y, YANG C,. An optic method based on LED reflection for measurement of the characteristics of particle suspension in a liquid-solid stirred tank[J]. The Chinese Journal of Process Engineering, 2011, 11(6): 933-937.
[35] LI X, YANG C, ZHANG G,. Experimental studies on suspension of solid particles in a low-shear stirred vessel[J]. Chem. Eng. Technol., 2011, 34(9): 1581-1586.
[36] TAMBURINI A, GENTILE L, CIPOLLINA A,. Experimental investigation of dilute solid-liquid suspension in an unbaffled stirred vessel by a novel pulsed laser based image analysis technique[J]. Chem. Eng. Trans., 2009, 17(1): 531-536.
[37] BRUCATO A, CIPOLLINA A, MICALE G,. Particle suspension in top-covered unbaffled tanks[J]. Chem. Eng. Sci., 2010, 65(10): 3001-3008.
[38] TAMBURINI A, BRUCATO A, BUSCIGLIO A,. Solid-liquid suspensions in top-covered unbaffled vessels: influence of particle size, liquid viscosity, impeller size, and clearance[J]. Ind. Eng. Chem. Res., 2014, 53(23): 9587-9599.
[39] TAMBURINI A, CIPOLLINA A, MICALE G,. Particle suspension in vortexing unbaffled stirred tanks[J]. Ind. Eng. Chem. Res., 2016, 55(27): 7535-7547.
[40] 来永斌, 杨敏官. 无挡板搅拌槽内固液悬浮的试验[J]. 江苏大学学报(自然科学版), 2010, 31(3): 309-313. LAI Y B, YANG M G. Experiment on solid-liquid suspension in unbaffled stirred tank[J]. Journal of Jiangsu University (Natural Science Edition), 2010, 31(3): 309-313.
[41] 杨锋苓, 周慎杰, 张翠勋, 等. 无挡板搅拌槽的固液悬浮特性[J]. 四川大学学报(工程科学版), 2014, 44(4): 185-190. YANG F L, ZHOU S J, ZHANG C X,. Solid-liquid suspension in an unbaffled stirred tank[J]. Journal of Sichuan University (Engineering Science Edition), 2014, 44(4): 185-190.
[42] WANG S, BOGER D V, WU J. Energy efficient solids suspension in an agitated vessel-water slurry[J]. Chem. Eng. Sci., 2012, 74: 233-243.
[43] WANG S, PARTHASARATHY R, BONG E Y,. Suspension of ultrahigh concentration solids in an agitated vessel[J]. AIChE J., 2012, 58(4): 1291-1298.
[44] WANG S, PARTHASARATHY R, WU J,. Optimum solids concentration in an agitated vessel[J]. Ind. Eng. Chem. Res., 2014, 53(10): 3959-3973.
[45] WU J, WANG S, NGUYEN B,. Improved viscous slurry agitation for minerals processing[J]. Miner. Eng., 2015, 78: 21-31.
[46] WU J, WANG S, NGUYEN B,. Improved mixing in a magnetite iron ore tankswirl flow: lab-scale and full-scale studies[J]. Chem. Eng. Technol., 2016, 39(3): 505-514.
[47] WANG S, JIANG M, IBRAHIM S,. Optimized stirred reactor for enhanced particle dispersion[J]. Chem. Eng. Technol., 2016, 39(4): 680-688.
[48] KIPKE K. Suspension by side entering agitator[J]. Chem. Eng. Process., 1984, 18(4): 233-238.
[49] CHEN J, XIAO W. Solids suspension study in a side-entering stirred tank through CFD modeling[J]. Int. J. Chem. Reactor Eng., 2013, 11(1): 331-346.
[50] 都荣礼, 黄雄斌, 王昕, 等. 侧伸式气液搅拌槽内的搅拌功率与传质性能[J]. 过程工程学报, 2008, 8(4): 709-713. DU R L, HUANG X B, WANG X,. Measurement of stirring power and mass transfer by a side-entering gas-liquid agitator[J]. The Chinese Journal of Process Engineering, 2008, 8(4): 709-713.
[51] 郑晓东, 黄雄斌, 都荣礼. 侧伸式搅拌槽固液悬浮性能[J]. 过程工程学报, 2009, 9(3): 417-423. ZHENG X D, HUANG X B, DU R L. Suspension of solid particles by side-entering agitators[J]. The Chinese Journal of Process Engineering, 2009, 9(3): 417-423.
[52] 李永纲, 黄雄斌. 立式圆槽内多轴搅拌器固-液悬浮性能[J]. 过程工程学报, 2012, 12(2): 181-186. LI Y G, HUANG X B. Solid-liquid suspension in a vertical three-impeller stirred tank[J]. The Chinese Journal of Process Engineering, 2012, 12(2): 181-186.
[53] TEZURA S, KIMURA A, YOSHIDA M,. Agitation requirements for complete solid suspension in an unbaffled agitated vessel with an unsteadily forward-reverse rotating impeller[J]. J. Chem. Technol. Biotechnol., 2007, 82(7): 672-680.
[54] YOSHIDA M, KIMURA A, YONEYAMA A,. Design and operation of unbaffled vessels agitated with an unsteadily forward-reverse rotating impeller handling solid-liquid dispersions[J]. Asia-Pac. J. Chem. Eng., 2012, 7(4): 572-580.
[55] 车占富. 斜插式搅拌器内部流场及固液悬浮特性的研究[D]. 镇江: 江苏大学, 2013. CHE Z F. Study on the flow field and solid-liquid suspension in an inclined inserted stirred tank[D]. Zhenjiang: Jiangsu University, 2013.
[56] 杨锋苓, 周慎杰, 张翠勋, 等. 偏心搅拌槽固液悬浮特性[J]. 过程工程学报, 2008, 8(6): 1064-1069. YANG F L, ZHOU S J, ZHANG C X,. Investigation on solid-liquid suspension performance in an eccentrically stirred tank[J]. The Chinese Journal of Process Engineering, 2008, 8(6): 1064-1069.
[57] 杨锋苓, 周慎杰, 张翠勋, 等. 偏心搅拌槽内固-液悬浮特性研究[J]. 华中科技大学学报(自然科学版), 2012, 40(11): 22-26. YANG F L, ZHOU S J, ZHANG C X,. Study on the solid-liquid suspension in eccentrically stirred tanks[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2012, 40(11): 22-26.
[58] GICALA B. Computational fluid dynamics modelling of a suspension of solid particles in a full scale unbaffled vessel[J]. Chem. Process Eng., 2009, 30(3): 475-484.
[59] 周坤. 偏心搅拌槽内固液两相流动特性的研究[D]. 北京: 北京化工大学, 2015. ZHOU K. Study for the flow characteristic of solid-liquid system in eccentrically stirred tank[D]. Beijing: Beijing University of Chemical Technology, 2015.
[60] MERSMANN A, WERNER F, MAURER S,. Theoretical prediction of the minimum stirrer speed in mechanically agitated suspensions[J]. Chem. Eng. Process., 1998, 37(6): 503-510.
[61] 张凤涛, 刘芳, 黄雄斌. 高固含搅拌槽内临界离底悬浮转速的数值模拟[J]. 过程工程学报, 2007, 7(3): 439-444. ZHANG F T, LIU F, HUANG X B. Numerical simulation of critical suspension impeller speed in a high concentration stirred tank[J]. The Chinese Journal of Process Engineering, 2007, 7(3): 439-444.
[62] ZWIETERING T N. Suspending of solid particles in liquid by agitators[J]. Chem. Eng. Sci., 1958, 8(3/4): 244-253.
[63] AYRANCI I, KRESTA S M. Critical analysis of Zwietering correlation for solids suspension in stirred tanks[J]. Chem. Eng. Res. Des., 2014, 92(3): 413-422.
[64] NARAYANAN S, BHATIA V K, GUHA D K,. Suspension of solids by mechanical agitation[J]. Chem. Eng. Sci., 1969, 24(2): 223-230.
[65] BRUCATO A, BRUCATO V. Unsuspended mass of solid particles in stirred tanks[J]. Can. J. Chem. Eng., 1998, 76(3): 420-427.
[66] GUHA D, RAMACHANDRAN P A, DUDUKOVIC M P. Flow field of suspended solids in a stirred tank reactor by Lagrangian tracking[J]. Chem. Eng. Sci., 2007, 62(22): 6143-6154.
[67] BALDI G, CONTI R, ALARIA E. Complete suspension of particles in mechanically agitated vessels[J]. Chem. Eng. Sci., 1978, 33(1): 21-25.
[68] NIENOW A W. Suspension of solid particles in turbine agitated baffled vessels[J]. Chem. Eng. Sci., 1968, 23(12): 1453-1459.
[69] ARMENANTE P M, NAGAMINE E U. Effect of flow off-bottom impeller clearance on the minimum agitation speed for complete suspension of solids in stirred tanks[J]. Chem. Eng. Sci., 1998, 53(9): 1757-1775.
[70] ARMENANTE P M, NAGAMINE E U, SUSANTO J. Determination of correlation to predict the minimum agitation speed for complete solid suspension in agitated vessels[J]. Can. J. Chem. Eng., 1998, 76(3): 413-419.
[71] MOLERUS O, LATZEL W. Suspension of solid particles in agitated vessels(Ⅰ): Archimedes numbers ≤ 40[J]. Chem. Eng. Sci., 1987, 42(6): 1423-1430.
[72] MOLERUS O, LATZEL W. Suspension of solid particles in agitated vessels(Ⅱ): Archimedes numbers > 40, reliable prediction of minimum stirrer angular velocities[J]. Chem. Eng. Sci., 1987, 42(6): 1431-1437.
[73] ARMENANTE P M, HUANG Y T, LI T. Determination of the minimum agitation speed to attain the just dispersed state in solid-liquid and liquid-liquid reactors provided with multiple impellers[J]. Chem. Eng. Sci., 1992, 47(9/10/11): 2865-2870.
[74] PAVLUSHENKO I S, KOSTIN N M, MATVEEV M S. Stirrer speeds in the stirring of suspensions[J]. J. Appl. Chem., 1957, 30: 1235-1243.
[75] NAGATA S. Mixing Principles and Applications[M]. New York: Halsted Press, 1975.
[76] KRAUME M. Mixing times in stirred suspensions[J]. Chem. Eng. Technol., 1992, 15(5): 313-318.
[77] HICKS M T, MYERS K J, BAKKER A. Cloud height in solids suspension agitation[J]. Chem. Eng. Commun., 1997, 160(1): 137-155.
[78] BOURNE J R, SHARMA R N. Homogeneous particle suspension in propeller-agitated flat bottom tanks[J]. Chem. Eng. J., 1974, 8(3): 243-250.
[79] MAC TAGGART R S, NASER-EL-DIN H A, MASLIYAH J H. Sample withdrawal from a slurry mixing tank[J]. Chem. Eng. Sci., 1993, 48(5): 921-923.
[80] BARRESI A A, KUZMANIĆ N, BALDI G. Continuous sampling of a slurry from a stirred vessel: analysis of the sampling efficiency and affecting parameters[J]. IChem. Symp. Ser., 1994, 136: 17-24.
[81] KUZMANIC N, KESSLER E M. Continuous sampling of floating solids suspension form a mixing tank[J]. Ind. Eng. Chem. Res., 1997, 36(11): 5015-5022.
[82] NASR-EL-DIN H, SHOOK C A, COLWELL A. A conductivity probe for measuring local concentrations in slurry systems[J]. Int. J. Multiphase Flow, 1987, 13(3): 365-378.
[83] MAC TAGGART R S, NASER-EL-DIN H A, MASLIYAH J H. A conductivity probe for measuring local solids concentration in a slurry mixing tank[J]. Sep. Technol., 1993, 3(3): 151-160.
[84] 黄雄斌, 闫宪斌, 施力田, 等. 固液搅拌槽内液相速度的分布[J]. 化工学报, 2002, 53(7): 717-722. HUANG X B, YAN X B, SHI L T,. Liquid velocity distributions in solid-liquid stirred vessels[J]. Journal of Chemical Industry and Engineering(China), 2002, 53(7): 717-722.
[85] MICALE G, GRISAFI F, BRUCATO A. Assessment of particle suspension conditions in stirred vessels by means of pressure gauge technique[J]. Chem. Eng. Res. Des., 2002, 80(8): 893-902.
[86] LASSAIGNE M, BLAIS B, FRADETTE L,. Experimental investigation of the mixing of viscous liquids and non-dilute concentrations of particles in a stirred tank[J]. Chem. Eng. Res. Des., 2016, 108(s): 55-68.
[87] BLAIS B, LASSAIGNE M, GONIVA C,. Development of an unresolved CFD-DEM model for the flow of viscous suspensions and its application to solid-liquid mixing[J]. J. Comput. Phys., 2016, 318: 201-221.
[88] 马国华, 霍元素, 王英琛, 等. 固液悬浮体系中固相浓度测量的新方法——光电测量法[J]. 化学工程, 1990, 18(1): 58-61. MA G H, HUO Y S, WANG Y C,. A new method for measurement of solid concentration in the solid-liquid suspension system—photoelectric measurement method[J]. Chemical Engineering(China), 1990, 18(1): 58-61.
[89] YAMAZAKI H, TOJO K, MIYANAMI K. Concentration profiles of solids suspended in a stirred tank[J]. Powder Technol., 1986, 48(3): 205-216.
[90] ANGST R, KRAUME M. Experimental investigations of stirred solid/liquid systems in three different scales: particle distribution and power consumption[J]. Chem. Eng. Sci., 2006, 61(9): 2864-2870.
[91] FERREIRA P J, RASTEIRO M G, FIGUEIREDO M M. A new approach to measuring solids concentration in mixing tanks[J]. Adv. Powder Tech., 1994, 5(1): 15-24.
[92] TAMBURINI A, CIPOLLINA A, MICALE G,. Particle distribution in dilute solid liquid unbaffled tanksa novel laser sheet and image analysis based technique[J]. Chem. Eng. Sci., 2013, 87: 341-358.
[93] MONTANTE G, MICALE G, MAGELLI F,. Experimental and CFD prediction of solid particle distribution in vessel agitated with four pitched blade turbines[J]. Chem. Eng. Res. Des., 2001, 79(8): 1005-1010.
[94] HOSSEINI S, PATEL D, EIN-MOZAFFARI F. Study of solid-liquid mixing in agitated tanks through electrical resistance tomography[J]. Chem. Eng. Sci., 2010, 65(4): 1374-1384.
[95] HUI L K, BENNINGTON C P J, DUMONT G A. Cavern formation in pulp suspensions using side-entering axial-flow impellers[J]. Chem. Eng. Sci., 2009, 64(3): 509-519.
[96] SARDESHPANDE M V, KUMAR G, ADITYA T,Mixing studies in unbaffled stirred tank reactor using electrical resistance tomography[J]. Flow Meas. Instrum., 2016, 47: 110-121.
[97] CARLETTI C, MONTANTE G, BLASIO C D,. Liquid mixing dynamics in slurry stirred tanks based on electrical resistance tomography[J]. Chem. Eng. Sci., 2016, 152: 478-487.
[98] LARACHI F, CHAOUKI J, KENNEDY G,. Radioactive particle tracking in multiphase reactor: principles and applications[M]// CHAOUKI J, LARACHI F, DUDUKOVIC M P. Non-invasive Monitoring of Multiphase Flows. Amsterdam: Elsevier, 1997: 335-406.
[99] RAMMOHAN A R, KEMOUN A, AL-DAHHAN M H,. Characterization of single phase flow in stirred tankscomputer automated radioactive particle tracking (CARPT)[J]. Chem. Eng. Res. Des., 2001, 79(8): 831-844.
[100] FANGARY Y S, BARIGOU M, SEVILLE J P K,. Fluid trajectories in a stirred vessel of non-Newtonian liquid using positron emission particle tracking[J]. Chem. Eng. Sci., 2000, 55(24): 5969-5979.
[101] FANGARY Y S, BARIGOU M, SEVILLE J P K,. A Langrangian study of solids suspension in a stirred vessel by positron emission particle tracking (PEPT)[J]. Chem. Eng. Technol., 2002, 25(5): 521-528.
[102] BARIGOU M. Particle tracking in opaque mixing systems: an overview of the capabilities of PET and PEPT[J]. Chem. Eng. Res. Des., 2004, 82(9): 1258-1267.
[103] FISHWICK R, WINTERBOTTOM M, PARKER D,. The use of positron emission particle tracking in the study of multiphase stirred tank reactor hydrodynamics[J]. Can. J. Chem. Eng., 2005, 83(1): 97-103.
[104] PIANKO-OPRYCH P, NIENOW A W, BARIGOU M. Positron emission particle tracking (PEPT) compared to particle image velocimetry (PIV) for studying the flow generated by a pitched-blade turbine in single-phase and multi-phase systems[J]. Chem. Eng. Sci., 2009, 64(23): 4955-4968.
[105] GUIDA A, NIENOW A W, BARIGOU M. PEPT measurements of solid-liquid flow field and spatial phase distribution in concentrated monodisperse stirred suspensions[J]. Chem. Eng. Sci., 2010, 65(6): 1905-1914.
[106] LIU L, BARIGOU M. Lagrangian particle tracking in mechanically agitated polydisperse suspensions: multi-component hydrodynamics and spatial distribution[J]. Int. J. Multiphase Flow, 2015, 73: 80-89.
[107] 黄正梁, 王靖岱, 阳永荣. 声波的多尺度分解与搅拌釜中浆液浓度的测量[J]. 化工学报, 2006, 57(9): 2062-2067. HUANG Z L, WANG J D, YANG Y R. Measurement of slurry concentration in stirred vessel based on AE measurement by wavelet transform[J]. Journal of Chemical Industry and Engineering(China), 2006, 57(9): 2062-2067.
[108] 任聪静, 王靖岱, 张晓欢, 等. 利用声发射技术测量搅拌釜的淤浆悬浮高度[J]. 化工学报, 2008, 59(6): 1383-1389. REN C J, WANG J D, ZHANG X H,. Measurement of slurry suspension height in stirred tank by multi-scale analysis of acoustic emission technology[J]. Journal of Chemical Industry and Engineering(China), 2008, 59(6): 1383-1389.
[109] 任聪静, 王靖岱, 阳永荣, 等. 声波测量在搅拌釜中固体颗粒临界悬浮转速测定的应用[J]. 化工学报, 2008, 59(8): 1986-1991. REN C J, WANG J D, YANG Y R,. Measurement of critical suspension speed for solid particles in stirred vessel based on acoustic method[J]. Journal of Chemical Industry and Engineering(China), 2008, 59(8): 1986-1991.
[110] 胡雨晨, 黄正梁, 王靖岱, 等. 基于Hilbert-Huang变换的搅拌釜临界悬浮转速的声发射测量[J]. 化工学报, 2012, 63(1): 36-41. HU Y C, HUANG Z L, WANG J D,. Measurement of critical suspension speed in stirred tank using acoustic emission technique based on Hilbert-Huang transform[J]. CIESC Journal, 2012, 63(1): 36-41.
[111] MONTANTE G, PAGLIANTI A, MAGELLI F. Analysis of dilute solid-liquid suspensions in turbulent stirred tanks[J]. Chem. Eng. Res. Des., 2012, 90(10): 1448-1456.
[112] FAN L, XU N. Experimental investigation of fibre particles in a turbulent stirred tank with DPIV[J]. Powder Technol., 2016. http://dx.doi.org/10.1016/j.powtec.2016.10.065
[113] GUIRAUD P, COSTES J, BERTRAND J. Local measurements of fluid and particle velocities in a stirred suspension[J]. Chem. Eng. J., 1997, 68(2): 75-86.
[114] DIETEMANN P, RUEFF M. A study of fibre suspension flow by means of Doppler ultrasound velocimetry and image analysis[C]//PAPTAC 90th Annual Meeting. Montreal, Que., Canada, 2004.
[115] EIN-MOZAFFARI F, BENNINGTON C P J, DUMONT G A,. Measuring flow velocity in pulp suspension mixing using ultrasonic Doppler velocimetry[J]. Chem. Eng. Res. Des., 2007, 85(5): 591-597.
[116] SARDESHPANDE M V, JUVEKAR V A, RANADE V V. Solid suspension in stirred tanks: UVP measurements and CFD simulations[J]. Can. J. Chem. Eng., 2011, 89(5): 1112-1121.
[117] SHAMLOU P A, KOUTSAKOS E. Solids suspension and distribution in liquids under turbulent agitation[J]. Chem. Eng. Sci., 1989, 44(3): 529-542.
[118] MAGELLI F, FAJNER D, NOCENTINI M,. Solid distribution in vessels stirred with multiple impellers[J]. Chem. Eng. Sci., 1990, 45(3): 615-625
[119] RASTEIRO M G, FIGUEIREDO M M, FREIRE C. Modelling slurry mixing tanks[J]. Adv. Powder Tech., 1994, 5(1): 1-14.
[120] SESSIECQ P, MIER P, GRUY F,. Solid particles concentration profiles in an agitated vessel[J]. Chem. Eng. Res. Des., 1999, 77(8): 741-746.
[121] MICALE G, MONTANTE G, GRISAFI F,. CFD simulation of particle distribution in stirred vessels[J]. Chem. Eng. Res. Des., 2000, 78(3): 435-444.
[122] DERKSEN J J. Highly resolved simulations of solids suspension in a small mixing tank[J]. AIChE J., 2012, 58(10): 3266-3278.
[123] MO J, GAO Z, BAO Y,. Suspending a solid sphere in laminar inertial liquid flow-experiments and simulations[J]. AIChE J., 2015, 61(4): 1455-1469.
[124] PRAKASH M, CLEARY P W, HA J,. Simulation of suspension of solids in a liquid in a mixing tank using SPH and comparison with physical modelling experiments[J]. Prog. Comput. Fluid Dyn., 2007, 7(2/3/4): 91-100.
[125] DECKER S, SOMMERFELD M. Calculation of particles suspension in agitated vessels with the Euler-Lagrange approach[J]. IChemE Symposium Series, 1996, 140: 71-82.
[126] CHEN X Q, PEREIRA J C F. Computational modeling of a dilute turbulent liquid-solid flow using a Eulerian-Lagrangian approach[J]. Int. J. Num. Methods Heat Fluid Flow, 2000, 10(4): 409-432.
[127] DERKSEN J J. Numerical simulation of solids suspension in a stirred tank[J]. AIChE J., 2003, 49(11): 2700-2714.
[128] ZHANG X, AHMADI G. Eulerian-Lagrangian simulations of liquid-gas-solid flows in three-phase slurry reactors[J]. Chem. Eng. Sci., 2005, 60(18): 5089-5104.
[129] SRINIVASA T, JAYANTI S. An Eulerian/Lagrangian study of solid suspension in stirred tanks[J]. AIChE J., 2007, 53(9): 2461-2469.
[130] LI Z P, DERKSEN J J, GAO Z M. Models and applications for simulating turbulent solid-liquid suspension in stirred tanks[J]. J. Chem. Eng. Jpn., 2015, 48(5): 329-336.
[131] CHOI Y, HUR N. A numerical study on particle suspension in a stirred vessel with Rushton turbine impeller[J]. J. Chem. Eng. Jpn., 2015, 48(5): 367-373.
[132] BARRUE H, BERTRAND J, CRISTOL B,. Eulerian simulation of dense solid-liquid suspension in multi-stage stirred vessel[J]. J. Chem. Eng. Jpn., 2001, 34(5): 585-594.
[133] KHOPKAR A R, KASAT G R, PANDIT A B,. Computational fluid dynamics simulation of the solid suspension in a stirred slurry reactor[J]. Ind. Eng. Chem. Res., 2006, 45(12): 4416-4428.
[134] MURTHY B N, GHADGE R S, JOSHI J B. CFD simulations of gas-liquid-solid stirred reactor: prediction of critical impeller speed for solid suspension[J]. Chem. Eng. Sci., 2007, 62(24): 7184-7195.
[135] KASAT G R, KHOPKAR A R, RANADE V V,. CFD simulation of liquid-phase mixing in solid-liquid stirred reactor[J]. Chem. Eng. Sci., 2008, 63(15): 3877-3885.
[136] GUHA D, RAMACHANDRAN M P, DUDUKOVIC M P,. Evaluation of large eddy simulation and Euler-Euler CFD models for solids flow dynamics in a stirred tank reactor[J]. AIChE J., 2008, 54(3): 766-778.
[137] TAMBURINI A, CIPOLLINA A, MICALE G,. Dense solid-liquid off-bottom suspension dynamics: simulation and experiment[J]. Chem. Eng. Res. Des., 2009, 87(4): 587-597.
[138] HOSSEINI S, PATEL D, EIN-MOZAFFARI F,. Study of solid-liquid mixing in agitated tanks through computational fluid dynamics modeling[J]. Ind. Eng. Chem. Res., 2010, 49(9): 4426-4435.
[139] PANNEERSELVAM R, SAVITHRI S, SURENDER G D. CFD modeling of gas-liquid-solid mechanically agitated contactor[J]. Chem. Eng. Res. Des., 2008, 86(12): 1331-1344.
[140] PANNEERSELVAM R, SAVITHRI S, SURENDER G D. Computational fluid dynamics simulation of solid suspension in a gas-liquid-solid mechanically agitated contactor[J]. Ind. Eng. Chem. Res., 2009, 48(3): 1608-1620.
[141] TAMBURINI A, CIPOLLINA A, MICALE G,. CFD simulations of dense solid-liquid suspensions in baffled stirred tanks: prediction of solid particle distribution[J]. Chem. Eng. J., 2013, 223: 875-890.
[142] TAMBURINI A, CIPOLLINA A, MICALE G,. CFD simulations of dense solid-liquid suspensions in baffled stirred tanks: prediction of suspension curves[J]. Chem. Eng. J., 2011, 178: 324-341.
[143] LJUNGQVIST M, RASMUSON A. Numerical simulation of the two-phase flow in an axially stirred vessel[J]. Chem. Eng. Res. Des., 2001, 79(5): 533-546.
[144] FLETCHER D F, BROWN G J. Numerical simulation of solid suspensionmechanical agitation: effect of the modeling approach, turbulence model and hindered settling drag law[J]. Int. J. Comp. Fluid Dynam., 2009, 23(2): 173-187.
[145] ZHU H P, ZHOU Z Y, YANG R Y,. Discrete particle simulation of particulate systems: theoretical developments[J]. Chem. Eng. Sci., 2007, 62(13): 3378-3396.
[146] ZHOU Z Y, KUANG S B, CHU K W,. Discrete particle simulation of particle-fluid flow: model formulations and their applicability[J]. J. Fluid Mech., 2010, 661: 482-510.
[147] SHAO T, HU Y Y, WANG W T,. Simulation of solid suspension in a stirred tank using CFD-DEM coupled approach[J]. Chin. J. Chem. Eng., 2013, 21(10): 1069-1081.
[148] PEPIOT P, DESJARDINS O. Numerical analysis of the dynamics of two- and three-dimensional fluidized bed reactors using a Euler-Lagrange approach[J]. Powder Technol., 2012, 220: 104-121.
[149] CAPECELATRO J, DESJARDINS O. A Euler-Lagrange strategy for simulating particle-laden flows[J]. J. Comput. Phys., 2013, 238: 1-31.
[150] GOHEL S, JOSHI S, AZHAR M,. CFD modeling of solid suspension in a stirred tank: effect of drag models and turbulent dispersion on cloud height[J]. Int. J. Chem. Eng., 2012. http://dx.doi.org/10.1155/2012/956975.
[151] LOPEZ DE BERTODANO M. Turbulent bubbly two-phase flow in a triangular duct[D]. New York: Rensselaer Polytechnic Institute, 1992.
[152] SIMONIN O, VIOLLET P L. Modelling of turbulent two-phase jets loaded withdiscrete particles[M]// HEWITT G F, MAYINGER F, RIZNIC J R. Phase-interface Phenomena in Multiphase Flow. New York: Hemisphere, 1990: 259-269.
[153] BURNS A D, FRANK T, HAMILL I,. The Favre averaged drag model for turbulent dispersion in Eulerian multi-phase flows[C]//Proceedings of the 5th International Conference on Multiphase Flow. Yokohama, Japan, 2004, 4: 1-17.
[154] SCHILLER L, NAUMANN Z. A drag coefficient correlation[J]. Z. Ver. Deutsch. Ing., 1935, 77: 318-323.
[155] MORSI S A, ALEXANDER A J. An investigation of particle trajectories in two-phase flow systems[J]. J. Fluid Mech., 1972, 55(2): 193-208.
[156] CLIFT R, GRACE J R, WEBER M E. Bubbles, Drops, and Particles[M]. New York: Academic Press, 1978.
[157] ISHII M, ZUBER N. Drag coefficient, relative velocity in bubbly, droplet or particulate flows[J]. AIChE J., 1979, 25(5): 843-55.
[158] GIBILARO L G, DI FELICE R, WALDRAM S P. Generalized friction factor and drag coefficient correlations for fluid-particle interactions[J]. Chem. Eng. Sci., 1985, 40(10): 1817-1823.
[159] GIDASPOW D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions[M]. San Diego: Academic Press, 1994.
[160] BRUCATO A, GRISAFI F, MONTANTE G. Particle drag coefficients in turbulent fluids[J]. Chem. Eng. Sci., 1998, 53(18): 3295-3314.
[161] HUILIN L, GIDASPOW D. Hydrodynamics of binary fluidization in a riser: CFD simulation using two granular temperatures[J]. Chem. Eng. Sci., 2003, 58(16): 3777-3792.
[162] OCHIENG A, ONYANGO M S. Drag models, solids concentration and velocity distribution in a stirred tank[J]. Powder Technol., 2008, 181(1): 1-8.
[163] TAMBURINI A, CIPOLLINA A, MICALE G,. Influence of drag and turbulence modeling on CFD predictions of solid liquid suspensions in stirred vessels[J]. Chem. Eng. Res. Des., 2014, 92(6): 1045-1063.
[164] WADNERKAR D, TADE M O, PAREEK V K,. CFD simulation of solid-liquid stirred tanks for low to dense solid loading systems[J]. Particuology, 2016, 29: 16-33.
[165] WEN C Y, YU Y H. Mechanics of fluidization[J]. Chem. Eng. Prog. Symp. Ser., 1966, 62: 100-111.
[166] ERGUN S. Fluid flow through packed columns[J]. Chem. Eng. Prog., 1952, 48(2): 89-94.
[167] PINELLI D, MONTANTE G, MAGELLI F. Dispersion coefficients and settling velocities of solids in slurry vessels stirred with different types of multiple impellers[J]. Chem. Eng. Sci., 2004, 59(15): 3081-3089.
[168] AUBIN J, FLETCHER D F, XUEREB C. Modeling turbulent flow in stirred tanks with CFD: the influence of the modelling approach, turbulence model and numerical scheme[J]. Exp. Therm. Fluid Sci., 2004, 28(5): 431-445.
[169] MONTANTE G, MAGELLI F. Modelling of solids distribution in stirred tanks: analysis of simulation strategies and comparison with experimental data[J]. Int. J. Comput. Fluid Dyn., 2005, 19(3): 253-262.
[170] FENG X, LI X Y, CHENG J C,. Numerical simulation of solid-liquid turbulent flow in a stirred tank with a two-phase explicit algebraic stress model[J]. Chem. Eng. Sci., 2012, 82: 272-284.
[171] DERKSEN J J. Long-time solids suspension simulations by means of a large-eddy approach[J]. Chem. Eng. Res. Des., 2006, 84(1): 38-46.
[172] DEEN N G, KUIPERS J A M. Direct numerical simulation (DNS) of mass, momentum and heat transfer in dense fluid-particle systems[J]. Curr. Opin. Chem. Eng., 2014, 5: 84-89.
[173] ŠVEC O, SKOČEK J, STANG H,. Free surface flow of a suspension of rigid particles in a non-Newtonian fluid: a lattice Boltzmann approach[J]. J. Non-Newtonian Fluid Mech., 2012, 179/180: 32-42.
[174] BISWAS P K, DEV S C, GODIWALLA K M,. Effect of some design parameters on the suspension characteristics of a mechanically agitated sand-water slurry system[J]. Mater. Des., 1999, 20(5): 253-265.
[175] ÖZCAN-TAŞKIN G, WEI H Y. The effect of impeller-to-tank diameter ratio on draw down of solids[J]. Chem. Eng. Sci., 2003, 58(10): 2011-2022.
[176] NOGUEIRA E S, PINTO J C, VIANNA JR A S. Analysis of energy dissipation in stirred suspension polymerisation reactors using computational fluid dynamics[J]. Can. J. Chem. Eng., 2012, 90(4): 983-995.
Progress of solid-liquid suspension in stirred vessel
YANG Fengling1,2, ZHOU Shenjie1,2
(1School of Mechanical Engineering, Shandong University, Jinan 250061, Shandong, China;2Key Laboratory of High-efficiency and Clean Mechanical Manufacture (Shandong University), Ministry of Education, Jinan 250061, Shandong, China)
Solid-liquid suspension is one of the typical unit operations in the process industry and accordingly, study on the suspension performance is of great importance. In this paper, developments of investigations on the solid-liquid suspension in stirred vessels in the past six decades were reviewed. Subsequently, configurations of the commonly used stirred systems were introduced. The critical suspension speeds of solid particles in baffled and unbaffled stirred vessels were clarified and compared. Finally, the principles of different experimental and numerical methods related with solid-liquid suspensions were presented. Investigations on the effect of free surface deformation on solids suspension and the research status were briefly summarized. The future development of numerical simulation on the solid-liquid suspension in stirred vessels is discussed.
stirred vessel; solid-liquid suspension; multiphase flow; free-surface; CFD
10.11949/j.issn.0438-1157.20161619
TQ 027
A
0438—1157(2017)06—2233—16
杨锋苓(1979—),男,博士,讲师。
国家自然科学基金项目(21306105);山东省重点研发计划项目(2016GGX103035)。
2016-11-15收到初稿,2017-03-09收到修改稿。
2016-11-15.
YANG Fengling, fly@sdu.edu.cn
supported by the National Natural Science Foundation of China (21306105) and the Key Development Foundation of Shandong Province(2016GGX103035).

