云南省不同生态水文分区参考作物蒸散量算法适用性评价
符 娜 宋孝玉 夏 露 李蓝君 孟春芳,2
(1.西安理工大学西北旱区生态水利工程国家重点实验室, 西安 710048;2.新乡水文水资源勘测局, 新乡 453000)
云南省不同生态水文分区参考作物蒸散量算法适用性评价
符 娜1宋孝玉1夏 露1李蓝君1孟春芳1,2
(1.西安理工大学西北旱区生态水利工程国家重点实验室, 西安 710048;2.新乡水文水资源勘测局, 新乡 453000)
将云南省分为3个区域(Ⅰ,滇西—滇西南山原与高山多水区;Ⅱ,滇西北—滇东北山原河谷中水区;Ⅲ,滇中北高原中水-少水区),基于36个气象站点1958—2013年逐日气象资料,以Penman-Monteith法为标准,利用线性回归法、均方根误差、平均偏差和Nash-Sutcliffe系数对Hargreaves-Samani法、Irmark-Allen法、Priestley-Taylor法、Makkink法、1948-Penman法、Penman-Van Bavel法、Turc法、FAO 24 Radiation法和Jensen-Haise法9种算法的计算精度进行对比。结果表明:1948-Penman法在云南省的适用性最强、计算精度最高,FAO 24 Radiation法与Jensen-Haise法误差较大,其中Ⅰ区适用性最好的是Hargreaves-Samani法,Ⅱ、Ⅲ区1—6月份为1948-Penman法,7—12月份为Priestley-Taylor法;在相对误差空间分布中,Ⅰ区Hargreaves-Samani法、Irmark-Allen法、Priestley-Taylor法、1948-Penman法的相对误差均在20%以下;Ⅱ、Ⅲ区中,Priestley-Taylor法、1948-Penman法的相对误差较小,为0~20%,同时在Ⅲ区中,Irmark-Allen法的相对误差也相对较小;因此,计算云南省的参考作物蒸散量时,整个区域推荐1948-Penman法,滇西—滇西南山原与高山多水区推荐Hargreaves-Samani法,滇西北—滇东北山原河谷中水区和滇中北高原中水-少水区推荐Priestley-Taylor法。
参考作物蒸散量; 云南省; 生态水文分区; 气象因子; 计算方法; 适用性评价
引言
参考作物蒸散量(Reference crop evapotranspiration,ET0)作为计算作物需水量及确保农田水分科学管理的关键性参数[1-2],是一项重要的农业与水文变量,对灌溉制度制定、流域规划及灌溉排水工程设计具有指导意义[3],同时也是区域水资源开发、利用与管理和农作物种植结构调整、区划与布局的重要依据[4]。目前ET0的确定方式主要分为实际测定或数学模拟两种,但在实际中通过仪器测定蒸散量具有一定的局限性,限制于一定区域且工作量大,造成结论难以推广,数学模拟法是基于各种气象因子建立数学模型估算,工作量相对较小,但由于不同的假定情况及输入要求等导致各种估算方法的精度存在差异[5],进而对估算结果有较大影响,因此,研究不同区域参考作物蒸散量算法的适用性非常必要。
按照研究区域具体特征,世界各国学者提出了诸多计算ET0的方法,主要分为辐射法、温度法、综合法和经验法等4种类型,具体有50多种计算方法[6]。1998年,国际粮农组织(FAO)提出了修正的Penman-Monteith公式[7],FAO 56 Penman-Monteith(P-M)法综合考虑了影响蒸散的各种因素,在气候条件差异较大地区(干旱、湿润或风速变化大等)的应用中取得了较好结果[8],国内一些研究成果也证实P-M法具有严谨的理论依据和较高的计算精度[9-12],作为不同区域ET0计算的标准方法被广泛认可。但该方法计算过程较复杂,并且对气象资料的要求高,在气象资料不完整的区域难以应用,因此很多简化的ET0估算方法应运而生,例如辐射法中的Priestley-Taylor法[13]、温度法中的Hargreaves-Samani法[14]、综合法中的Penman-Van Bavel法[15]和经验法中的Irmark-Allen法[16]等。但这些计算方法易受研究区自然环境、地形地貌、气候特征等因素以及模型数学机理的影响,其在不同区域的计算精度存在显著差异,因而,各ET0简化算法在应用时需根据不同区域情况进行适用性评价。
云南省河流众多,水资源丰富,但受降水量时空分布不均的影响,季节性干旱缺水问题突出,水资源供需问题日益显著。省内地形地貌复杂多变、气候条件特殊且差异较大,受气候因子等的影响,ET0在不同区域变化显著,但目前针对云南省不同分区ET0简化算法的研究鲜见报道,进而造成了水资源配置上的盲目性。本文根据云南省不同生态水文分区,采用应用较广泛的FAO 56 Penman-Monteith法、Hargreaves-Samani法、Irmark-Allen法、Priestley-Taylor法、Makkink法、1948-Penman法、Penman-Van Bavel法、Turc法、FAO 24 Radiation法和Jensen-Haise法等10种方法分别计算各生态水文分区参考作物蒸散量,并以FAO 56 Penman-Monteith法作为标准方法,对其他9种算法进行评价,寻求适合云南省不同生态水文分区的ET0简化算法,为云南省农业水资源优化管理和高效利用提供科学依据。
1 研究区概况及数据来源
1.1 研究区概况
云南省位处我国西南边陲,面积38.32万km2,占全国面积的4.1%。作为高原山地省区,云南省山地面积占全省总面积的94%,河谷盆地面积仅占6%,地势西北高、东南低,属于低纬度高原季风气候,日温差大,年温差小,干湿季分明,气温随地势高低呈垂直变化趋势明显。大部分地区年降水量在1 000 mm以上,但时空分布极不均匀,年内84.2%的降水集中在5—10月份的雨季,11月份—翌年4月份为旱季。结合资料系列的完整性,本研究选取云南省36个代表性站点,根据郭建威[17]的研究成果,按照自然地理、气候、水系等特征,将云南省分为滇西—滇西南山原与高山多水区(I)、滇西北—滇东北山原河谷中水区(Ⅱ)和滇中北高原中水-少水区(Ⅲ)3个生态水文分区,分区及站点分布情况见图1。在众多的分区影响因素中,将径流深、河道平均比降、降水量和人均GDP 4个指标作为生态水文分区的决定因素,具体分区特征见表1。
1.2 数据来源
采用的气象数据来自中国气象科学数据共享服务网,在保证站点数量的前提下,剔除气象资料缺测较多的站点,对部分站点的缺测数据进行线性内插法补全,整理后得到云南省36个气象站点1958—2013年逐日地面气象观测资料,包括日平均风速、日照时数、日降水量、日最高气温、日最低气温、日平均气温、日平均相对湿度、日平均水汽压等数据。
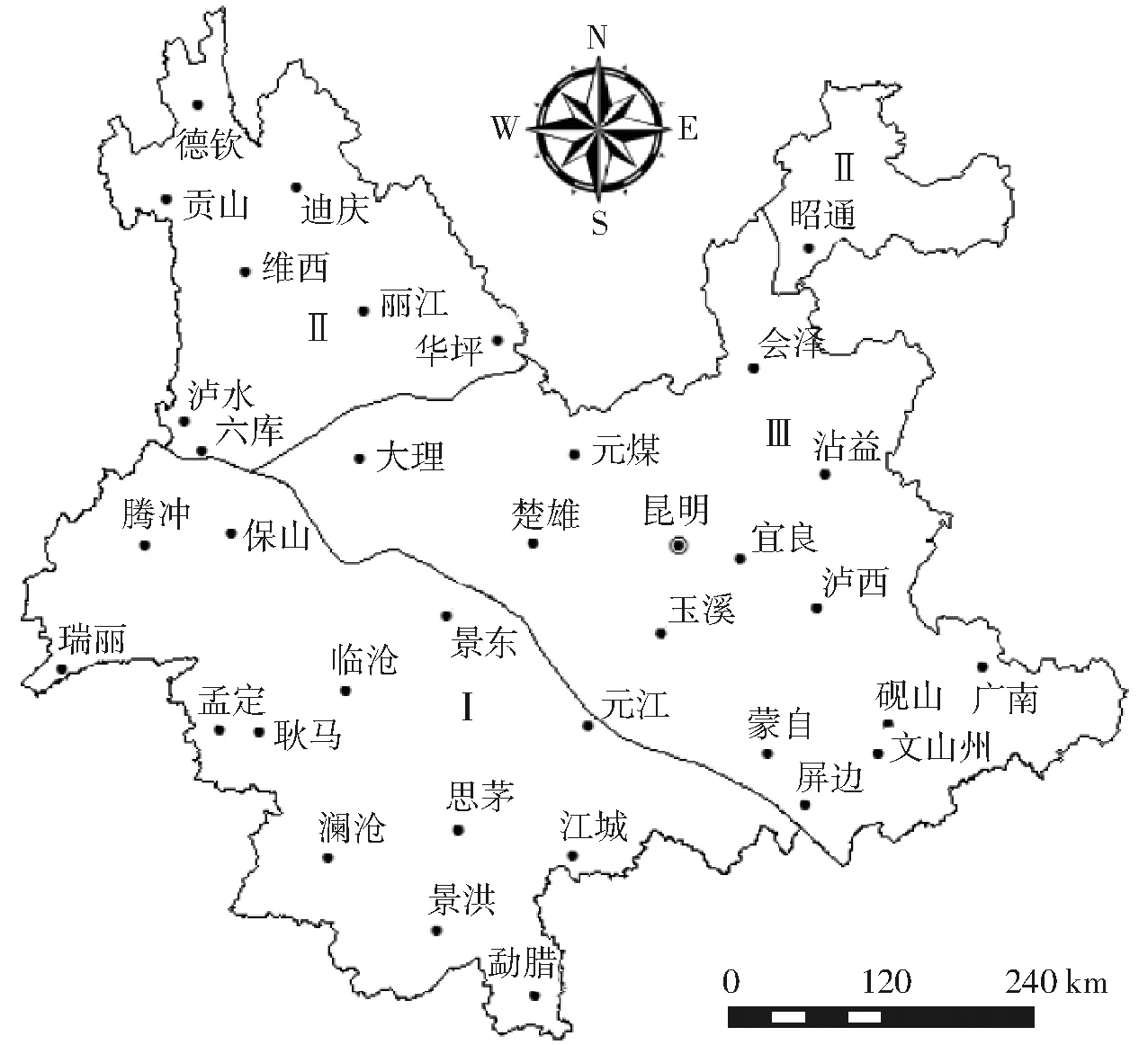
图1 云南省不同生态水文分区及站点分布图Fig.1 Area division and stations distribution in Yunnan Province

表1 云南省不同生态水文分区特征统计Tab.1 Characteristics statistic of different eco-hydrological regionalization in Yunnan Province
2 研究方法
2.1 参考作物蒸散量计算方法
(1)Penman-Monteith法
Penman-Monteith法以能量平衡和水汽扩散论为基础,同时考虑作物的生理特征和空气动力学参数的变化,具有较充分的理论依据和较高的计算精度[18],公式为
(1)
式中Δ——饱和水汽压与温度关系曲线在T处的切线斜率,kPa/℃
Rn——冠层表面净辐射,MJ/(m2·d)
G——土壤热通量,MJ/(m2·d)
γ——干湿计常数,kPa/℃
T——平均温度,℃
u2——2 m高处的平均风速,m/s
ea——实际水汽压,kPa
ed——饱和水汽压,kPa
(2)Hargreaves-Samani法
Hargreaves-Samani法主要考虑平均温度和昼夜温差的影响[14],同时利用大气顶层辐射进行计算,计算误差有随海拔逐渐升高的趋势,在云南省的低海拔地区适用性范围较广,公式为
ET0-HS=C0(Tmax-Tmin)0.5(Tmean+17.8)Ra
(2)
式中ET0-HS——Hargreaves-Samani法计算得到的ET0,mm/d
C0——转换系数,取0.000 936
Tmax、Tmin、Tmean——日最高、最低和平均温度,℃
Ra——大气顶层辐射量,MJ/(m2·d)
(3)Irmark-Allen法
Irmark-Allen法是由IRMARK等根据美国湿润地区资料得到的模拟模型,在湿润地区适用性较好[16],公式为
ET0-IA=0.489+0.289Rn+0.002 3Tmean
(3)
式中ET0-IA——Irmark-Allen法计算得到的ET0,mm/d
(4)Priestley-Taylor法
Priestley-Taylor法基于辐射量进行计算[13],所采用的形式对空气动力学项进行了修正,将空气动力学项折算为辐射量的0.26倍,其精度较之前有所提高,且计算变得相对简便,公式为
(4)
式中ET0-PT——Priestley-Taylor法计算得到的ET0,mm/d
λ——水的汽化潜热,取2.45 MJ/kg
(5)Makkink法
Makkink法是在太阳辐射量基础上提出,该方法在寒冷地区的适用性得到广泛验证[19],公式为
(5)
式中ET0-MK——Makkink法计算得到的ET0,mm/dRs——太阳辐射量,MJ/(m2·d)
(6)1948-Penman法
1948-Penman法采用与FAO 56 Penman-Monteith法不同的空气动力学项,适用于温度较高且空气湿度较小地区[20],公式为
(6)
式中ET0-48PM——1948-Penman法计算得到的ET0,mm/d
(7)Penman-Van Bavel法
Penman-Van Bavel法在海拔高度相对较低与日温差相差较小的条件下适用性较好[15],公式为
(7)
其中
rs=80.8/(u2+0.1)
式中ET0-PVB——Penman-Van Bavel法计算得到的ET0,mm/d
(8)Turc法
Turc法是基于欧洲西部区域提出的[21],被广泛推荐作为湿润地区的估算方法[22],公式为
(8)
式中ET0-Tu——Turc法计算得到的ET0,mm/d
(9)FAO 24 Radiation法
FAO 24 Radiation法源于Makkink公式,主要根据太阳辐射资料来估算参考作物蒸散量[23],计算误差在低海拔高度地区较小,随海拔高度升高,其准确度需要进一步研究,公式为
(9)
其中
式中ET0-FAO24——FAO 24 Radiation法计算得到的ET0,mm/d
ud——白昼平均风速,m/s
RH——平均相对湿度,%
a——参数,取-0.3
(10)Jensen-Haise法
Jensen-Haise法是通过土壤取样,评估了很多蒸散发观测值之后,得到的经验公式[22],因云南红壤分布较为广泛,故选取此方法作为计算方法之一,公式为
(10)
式中ET0-JH——Jensen-Haise法计算得到的ET0,mm/d
N——日照的最大可能时数,h
n——实际日照时数,h
采用以上10种方法对ET0进行模拟计算,以FAO推荐的Penman-Monteith法作为ET0计算的标准方法,对其他9种简易计算方法进行评估。
2.2 评价方法
以FAO 56 Penman-Monteith法计算的ET0作为标准,采用线性回归法、均方根误差(RMSE)、平均偏差(MBE)和Nash-Sutcliffe系数(CD)来评价其他9种算法与标准算法计算结果相比的适用性及精度[24-26],具体公式分别为
(11)
(12)
(13)

其中,RMSE与MBE的值越小、CD的值越大,该算法偏离标准算法的程度越小,与FAO 56 Penman-Monteith法的一致性越好、计算精度越高,对研究区的适用性越强。
3 结果与分析
3.1 云南省不同生态水文分区ET0算法日均值评价
3.1.1 不同ET0算法的适用性评价
云南省不同生态水文分区不同ET0简化算法与P-M法日值之间的回归系数及决定系数见表2。结果显示,云南省不同生态水文分区1948-Penman法、FAO 24 Radiation法与FAO 56 Penman-Monteith法拟合的回归方程斜率均大于1,表明有不同程度偏大,且不同生态水文分区1948-Penman法的决定系数R2均为0.99,与FAO 56 Penman-Monteith法的相关性最显著,其他7种方法Hargreaves-Samani法、Irmark-Allen法、Priestley-Taylor法、Makkink法、Penman-Van Bavel法、Turc法、Jensen-Haise法相比FAO 56 Penman-Monteith法的结果则偏小。其中,在Ⅰ区Priestley-Taylor法、1948-Penman法与FAO 56 Penman-Monteith法拟合的回归方程斜率更接近1,分别为0.88、1.17,除Irmark-Allen法与Jensen-Haise法外其他7种ET0简化算法拟合方程的决定系数R2均在0.85以上,达到极显著水平(p<0.01);在Ⅱ区、Ⅲ区的拟合方程斜率最接近1的均为1948-Penman法,斜率分别为1.15和1.10,决定系数R2达到极显著水平的均为1948-Penman法和FAO 24 Radiation法,Ⅱ区为0.99和0.86,Ⅲ区为0.99和0.94。不同算法在云南省拟合方程的决定系数R2达到极显著水平的有Priestley-Taylor法、Makkink法、1948-Penman法、Penman-Van Bavel法和FAO 24 Radiation法,决定系数R2分别为0.85、0.85、0.94、0.99、0.85,其中,Priestley-Taylor法、1948-Penman法在Ⅰ区的适用性较强,1948-Penman法在Ⅱ区与Ⅲ区的适用性较强,且1948-Penman法在整个云南省的适用性均为最强。

表2 云南省不同生态水文分区不同ET0简化算法与P-M法日值之间的回归系数及决定系数Tab.2 Regression coefficients and determination coefficients between different daily ET0 simplification methods and P-M method in different eco-hydrological regionalization of Yunnan Province
注:** 表示拟合效果达到p<0.01的极显著水平。
3.1.2 不同ET0算法的精度对比
表3为云南省不同生态水文分区9种ET0简化算法与Penman-Monteith法的均方根误差(RMSE)、平均偏差(MSE)和Nash-Sutcliffe系数(CD)对比结果。根据RMSE的结果,其值越小,表明2种方法之间的关系越密切,差异越小;MBE越接近0,差异越小;CD越大,则说明该算法与P-M法的一致性较好。研究表明:Ⅰ区各项指标中,Irmark-Allen法、Priestley-Taylor法、1948-Penman法表现良好,其RMSE值在0.20~0.57 mm/d之间,MBE值为0.26~0.44 mm/d,CD值为0.52~0.76,其中1948-Penman法的精度最高,其CD值达到0.76,其次是Priestley-Taylor法和Irmark-Allen法,其他方法的CD系数均较小,其中FAO 24 Radiation法计算精度最低,其RMSE、MBE、CD值分别为103.15 mm/d、3.24 mm/d和-14.29。Ⅱ区Priestley-Taylor法精度最高,其RMSE为0.28 mm/d,MBE则达到了0.01 mm/d,而CD值达到了0.71,计算精度明显高于其他方法,1948-Penman法和Irmark-Allen法精度次之,FAO 24 Radiation法与Jensen-Haise法精度较低,RMSE值均在9.59 mm/d以上,CD值小于-3.07。Ⅲ区1948-Penman法的计算精度最高,RMSE值为0.18 mm/d,MBE值为0.45 mm/d,而CD值则达到了0.83,其他方法中,RMSE均大于0.72 mm/d,最大值为114.07 mm/d,MBE值在-1.57~3.19 mm/d之间,CD最小值为-7.54,其精度较1948-Penman法低。通过对整个云南省的模拟精度分析可以得出,1948-Penman法的精度最高,其RMSE、MBE、CD值分别为0.19 mm/d、0.44 mm/d、0.78,FAO 24 Radiation法精度最低,其RMSE、MBE、CD值分别为97.22 mm/d、3.09 mm/d、-10.80。因此,1948-Penman法在云南省的计算精度最高,可作为云南省ET0简化计算推荐方法。

表3 云南省不同生态水文分区不同ET0简化算法精度对比Tab.3 Comparison of ET0 calculation accuracy among simplification methods in different eco-hydrological regionalization of Yunnan Province
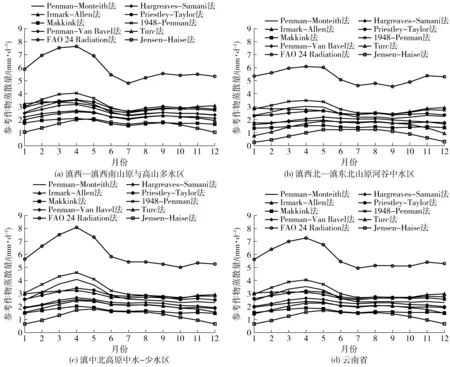
图2 云南省不同生态水文分区9种ET0简化算法与Penman-Monteith法逐月ET0计算结果对比Fig.2 Comparison of monthly ET0 calculated by Penman-Monteith and other nine models of different eco-hydrological regionalization in Yunnan Province
3.2 云南省不同生态水文分区ET0算法月均值评价
云南省不同生态水文分区9种ET0简化算法与Penman-Monteith法逐月ET0均值对比结果见图2。结果表明:不同ET0简化算法计算得到的ET0月均值在年内变化趋势基本一致,总体呈现先增加后减小的二次抛物线形式。在不同生态水文分区,大多数算法的计算结果为7月份的ET0最小,4月份最大,其中结果有较大差异的算法是Jensen-Haise方法,在3个区域中的表现为1月份和12月份最小,5月份最大。以Penman-Monteith法作为参考标准,可以看出,3个区域中1948-Penman法、FAO 24 Radiation法计算结果均在Penman-Monteith法之上,结果偏大,Hargreaves-Samani法、Makkink法、Penman-Van Bavel法、Turc法、Jensen-Haise法的计算结果均在Penman-Monteith法之下,结果偏小,而Priestley-Taylor法、Irmark-Allen法在Ⅰ区偏大,在Ⅱ、Ⅲ区的1—6月份结果偏小,7—12月份结果偏大。从月均值变化来看,Ⅰ区Hargreaves-Samani法在所有月份中计算最为准确,Ⅱ、Ⅲ区1—6月份中1948-Penman法的计算结果较为接近Penman-Monteith法,7—12月份中Priestley-Taylor法的估算结果较为准确。

图3 云南省不同生态水文分区9种ET0简化算法结果与Penman-Monteith法的相对误差空间分布Fig.3 Spatial distributions of relative error of nine simplification methods of different eco-hydrological regionalization in Yunnan Province compared with Penman-Monteith method
3.3 云南省不同生态水文分区ET0算法空间适用性评价
云南省不同生态水文分区9种ET0简化算法结果与Penman-Monteith法的相对误差空间分布如图3所示。研究表明:在Ⅰ区中,Hargreaves-Samani法、Irmark-Allen法、Priestley-Taylor法、1948-Penman法4种方法的相对误差(RE)介于0~20%之间,适用性较好,Penman-Van Bavel法、Turc法在Ⅰ区中表现为部分地区RE小于20%,而在剩余部分其RE则扩大至20%~40%,Makkink法在Ⅰ区中其RE为20%~40%,Jensen-Haise法大部分地区RE为40%~60%,仅在靠近边境地区的瑞丽、孟定、耿马、景洪、勐腊站点RE降至20%以下,而FAO 24 Radiation法在Ⅰ区的计算结果明显偏大,其RE除元江站点值在100%以下,其余地区的RE均超过100%。在Ⅱ区的RE空间分布中,仅有Priestley-Taylor法的RE小于20%,其适用性明显高于其他方法,1948-Penman法和Irmark-Allen法除德钦、迪庆2个站点的RE超过20%外,其余地区RE也在20%以下,Hargreaves-Samani法、Penman-Van Bavel法在Ⅱ区中西北部地区部分站点的RE在20%以下,其余大部分Ⅱ区的RE在20%~40%范围内,Makkink法的RE空间分布与Turc法相比看出,这2种方法在Ⅱ区的空间分布中表现为适用性的相互补充,其RE范围总体为20%~60%,Jensen-Haise法在Ⅱ区中大部分区域的RE在60%~80%之间,在德钦、迪庆站点达到了80%以上,这表明该方法在Ⅱ区适用性较差,FAO 24 Radiation法在Ⅱ区RE除元谋站点外,其他站点的RE在100%以上。在Ⅲ区中,Irmark-Allen法、Priestley-Taylor法、1948-Penman法的RE均在20%以下,表明这3种方法在Ⅲ区适用性高于其他方法,而Hargreaves-Samani法在Ⅲ区的RE出现了南北差异,从图中可以看出在Ⅲ区的南部地区其RE小于20%,而北部地区RE在20%~40%之间,Penman-Van Bavel法、Turc法的RE均在20%~40%之间,适用性较差,Makkink法、FAO 24 Radiation法、Jensen-Haise法的RE均大于40%,FAO 24 Radiation法在部分地区达到100%以上,表明这3种方法在Ⅲ区适用性较差。Priestley-Taylor法、1948-Penman法在整个云南省的RE基本在20%以下,这2种方法在整个云南省适用性较好。Hargreaves-Samani法主要考虑平均温度和昼夜温差的影响,同时利用大气顶层辐射量进行计算,其中Ⅰ区地势起伏变化不大,日温度变化幅度较小,计算结果较为准确,Ⅱ、Ⅲ区随着海拔高度升高,日温度变化较大,导致RE在Ⅰ区的适用性高于其他2个区,Makkink法、Turc法、Jensen-Haise法在Ⅰ、Ⅱ、Ⅲ区的RE随着纬度的增加,精度逐渐降低,表明这3种方法在低纬度地区适用性高于高纬度地区。Irmark-Allen法仅在云南省西北部高寒地区适用性表现变差,其余地区表现较好。而FAO 24 Radiation法在整个云南省的适用性偏差较大,不能真实反映地区的参考作物蒸散量。
4 讨论
国内外有关大区域ET0算法适用性评价的研究较少。KISI[27]研究Turkey的Isparta等5个站点的ET0,得出Vail-T-Rs法和Hargreaves-Samani法在研究区内的计算精度较高。樊军等[8]对陕西省3个站点进行研究,得出Penman系列方法之间关系密切,Kimberly PM-72法最佳的结论。为避免评价的局限性,本文选取整个云南省36个站点作为研究对象,具有各分区跨幅大、站点分布广的特点。结果显示,1948-Penman法、FAO 24 Radiation法与FAO 56 Penman-Monteith法相比有不同程度偏大,Hargreaves-Samani法、Irmark-Allen法、Priestley-Taylor法、Makkink法、Penman-Van Bavel法、Turc法、Jensen-Haise法的结果偏小。其中1948-Penman法在不同生态水文分区的决定系数R2均为0.99,与FAO 56 Penman-Monteith法的相关性最显著,1948-Penman法在整个云南省的适用性最强、计算精度最高,可作为云南省ET0简化计算推荐方法,这与贾悦等[3]研究长江流域得出长江上游内综合法的计算精度较高于温度法的结论一致。而FAO 24 Radiation法计算精度最低,其RMSE、MBE、CD值分别为103.15 mm/d、3.24 mm/d和-14.29,造成其精度较低的主要原因在于FAO 24 Radiation公式中的常数项a为经验值,但许多学者通过分析各自的资料得到了不同的a值,并发现其具有日变化和季节变化,因此若将a值当做常数计算,则会造成一定的偏差,从而在对云南省运用该公式时,需根据当地资料进行经验系数的修正。
各生态水文分区的最佳ET0简化算法不同。在滇西-滇西南山原与高山多水区中,9中方法中Hargreaves-Samani法、Irmark-Allen法、Priestley-Taylor法、1948-Penman法的计算精度较高,其RE都小于20%;在滇西北—滇东北山原河谷中水区的方法适用性研究中,得出Priestley-Taylor法和1948-Penman法适用性最高;而在滇中北高原中水-少水区内,Irmark-Allen法、Priestley-Taylor法、1948-Penman法较其余方法的RE低,适用性较强。这与李晨等[6]利用46个站点对四川省不同区域参考作物蒸散量计算方法适用性的研究得出川西南地区表现最好的方法为Priestley-Taylor法的结论一致。
因不同类型ET0简化算法的空间适应性不同,因此分析各方法在不同地域上适用性。Hargreaves-Samani法主要考虑平均温度和昼夜温差的影响,同时利用大气顶层辐射进行计算,其中Ⅰ区地势起伏变化不大,日温度变化幅度较小,计算结果较为准确,Ⅱ、Ⅲ区随着海拔高度升高,日温度变化较大,导致RE在Ⅰ区的适用性高于其他2个区,Makkink法、Turc法、Jensen-Haise法在Ⅰ、Ⅱ、Ⅲ区的RE随着纬度的增加,精度逐渐降低,表明这3种方法在低纬度地区适用性高于高纬度地区,与杜加强等[28]得出的基于温度的算法在低海拔高度站点、生长季与P-M结果的一致性要高于高海拔高度站点、非生长季的结论一致。Irmark-Allen法仅在云南省西北部高寒地区适用性表现变差,其余地区表现较好。而FAO 24 Radiation法在整个云南省的适用性偏差较大,不能真实反映地区的参考作物蒸散量。由于辐射法中的Priestley-Taylor法主要考虑太阳辐射量,云南省作为我国低纬度高海拔地区,其辐射量较大,同时气候垂直分布明显,温度日较差大,所以Priestley-Taylor法在整个云南地区计算精度较高,符合WEIB等[29]得出的Priestley-Taylor方法较适宜于在全球尺度应用的结论。同时,本研究中未对云南省部分气候独特地区进行方法的适用性研究,例如元谋干热河谷地区、海拔高度落差较大的山谷地区等地区,需要在后期工作中继续研究。
5 结论
(1)1948-Penman法在整个云南省的适用性最强、计算精度最高,可作为云南省ET0简化计算推荐方法。此外,在滇西—滇西南山原与高山多水区Priestley-Taylor法的适用性较强,其计算精度较高,FAO 24 Radiation法计算精度最低;滇西北—滇东北山原河谷中水区Priestley-Taylor法和Irmark-Allen法的计算精度较高,FAO 24 Radiation法与Jensen-Haise法精度较低。
(2)云南省不同生态水文分区中,滇西—滇西南山原与高山多水区中Hargreaves-Samani法更接近于Penman-Monteith法的计算结果,曲线的拟合程度较高,因此在云南省滇西—滇西南山原与高山多水区缺少辐射和风速资料的站点,可以考虑利用Hargreaves-Samani法代替Penman-Monteith法;在滇西北—滇东北山原河谷中水区、滇中北高原中水-少水区的1—6月份中1948-Penman法的精度较其他方法较高,此方法可以适用于滇西北—滇东北山原河谷中水区、滇中北高原中水-少水区中湿润下垫面站点的计算;在滇西北—滇东北山原河谷中水区、滇中北高原中水-少水区的7—12月份中Priestley-Taylor法的估算结果较为准确,因此在滇西北—滇东北山原河谷中水区、滇中北高原中水-少水区中缺少空气动力学资料时,Priestley-Taylor法可以用来计算参考作物蒸散量。
(3)Hargreaves-Samani法等9种ET0简化算法的空间差异性明显。Hargreaves-Samani法、Irmark-Allen法、Priestley-Taylor法、1948-Penman法在在滇西—滇西南山原与高山多水区中精度较高,其RE小于20%;在滇西北—滇东北山原河谷中水区中,相对误差最小的是Priestley-Taylor法、1948-Penman法;在滇中北高原中水-少水区内,Irmark-Allen法、Priestley-Taylor法、1948-Penman法适用性较其他方法高。
1 赵璐,梁川,崔宁博,等.不同ET0计算方法在川中丘陵地区的比较及改进[J].农业工程学报,2012,28(24):92-98. ZHAO Lu,LIANG Chuan,CUI Ningbo,et al.Comparison and improvement of different calculation methods forET0in hilly area of central Sichuan Basin[J].Transactions of the CSAE,2012,28(24):92-98.(in Chinese)
2 张倩,段爱旺,高阳,等.基于温度资料估算参考作物腾发量的方法比较[J/OL].农业机械学报,2015,46(2):104-109.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150216& journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.02.016. ZHANG Qian,DUAN Aiwang,GAO Yang,et al.Comparative analysis of reference evapotranspiration estimation methods using temperature data[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2015,46(2):104-109.(in Chinese)
3 贾悦,崔宁博,魏新平,等.基于反距离权重法的长江流域参考作物蒸散量算法适用性评价[J].农业工程学报,2016,32(6):130-138. JIA Yue,CUI Ningbo,WEI Xinping,et al.Applicability evaluation of different algorithms for reference crop evapotranspiration in Yangtze River Basin based on inverse distance weighted method[J].Transactions of the CSAE,2016,32(6):130-138.(in Chinese)
4 杨永红,张展羽,阮新建.西藏参考作物蒸发蒸腾量的时空变异规律[J].水科学进展,2009,20(6):775-781. YANG Yonghong,ZHANG Zhanyu,RUAN Xinjian.Temporal and spatial variation law of reference crop evapotranspiration in Tibet[J].Advances in Water Science,2009,20(6):775-781.(in Chinese)
5 李志.参考作物蒸散简易估算方法在黄土高原的适用性[J].农业工程学报,2012,28(6):106-111. LI Zhi.Applicability of simple estimating method for reference crop evapotranspiration in Loess Plateau[J].Transactions of the CSAE,2012,28(6):106-111.(in Chinese)
6 李晨,崔宁博,冯禹,等.四川省不同区域参考作物蒸散量计算方法的适用性评价[J].农业工程学报,2016,32(4):127-134. LI Chen,CUI Ningbo,FENG Yu,et al.Adaptation evaluation for reference evapotranspiration methods in different regions of Sichuan[J].Transactions of the CSAE,2016,32(4):127-134.(in Chinese)
7 ALLEN R G,PEREIRA L S,RAES D,et al.Crop evapotranspiration:guidelines for computing crop water requirements[R].Rome:FAO Irrigation and Drainage,1998.
8 樊军,邵明安,王全九.黄土区参考作物蒸散量多种计算方法的比较研究[J].农业工程学报,2008,24(3):98-102. FAN Jun,SHAO Ming’an,WANG Quanjiu.Comparisons of many equations for calculating reference evapotranspiration in the Loess Plateau of China[J].Transactions of the CSAE,2008,24(3):98-102.(in Chinese)
9 曹雯,申双和,段春锋. 西北地区生长季参考作物蒸散变化成因的定量分析[J].地理学报,2011,66(3):407-415. CAO Wen,SHEN Shuanghe,DUAN Chunfeng.Quantification of the causes for reference crop eapotranspiration changes in growing season in Northwest China [J].Acta Geographica Sinica,2011,66(3):407-415.(in Chinese)
10 姬兴杰,朱业玉,顾万龙.河南省参考作物蒸散量变化特征及其气候影响分析[J].中国农业气象,2013,34(1):14-22. JI Xingjie,ZHU Yeyu,GU Wanlong.Analysis on trends in annual reference crop evapotranspiration and its impact climatic factors in Henan province during 1971 to 2010[J].Chinese Journal of Agrometeorology,2013,34(1):14-22.(in Chinese)
11 冯禹,崔宁博,魏新平,等.川中丘陵区参考作物蒸散量时空变化特征与成因分析[J].农业工程学报,2014,30(14):78-86. FENG Yu,CUI Ningbo,WEI Xinping,et al.Temporal-spatial distribution characteristics and causes analysis of reference crop evapotranspiration in hilly area of central Sichuan [J].Transactions of the CSAE,2014,30(14):78-86.(in Chinese)
12 王卫光,邢万秋,彭世彰,等.海河流域50年来参考腾发量的时空变化规律及其影响原因[J].应用基础与工程科学学报,2012,20(2):237-252. WANG Weiguang,XING Wanqiu,PENG Shizhang,et al.Spatial and temporal patterns of reference evapotranspiration changes and their causes in the Haihe River Basin during the past 50 years,China [J].Journal of Basic Science and Engineering,2012,20(2):237-252.(in Chinese)
13 PRIESTLEY C H,TAYLOR R J.On the assessment of surface heat flux and evapotranspiration using large-scale parameters[J].Monthly Weather Review,1972,100(2):81-92.
14 HARGREAVES G H,ALLEN R G.History and evaluation of Hargreaves evapotranspiration equation[J].ASCE Jounal of Irrigation and Drainage Engineering,2003,129(1):53-63.
15 VAN BAVEL C H M.Potential evapotranspiration:the combination concept and its experimental verification[J].Water Resources Research,1966,2(3):23-34.
16 IRMAK S,IRMAK A,ALLEN R S,et al.Solar and net radiation-based equations to estimate reference evapotranspiration in humid climate[J].ASCE Journal of Irrigation and Drainage Engineering,2003,129(5):336-347.
17 郭建威.云南省山区性中小河流生态环境流量研究[D].武汉:长江科学院,2011. GUO Jianwei.Study of eco-environmental flow from medium and small mountain rivers in Yunnan Province[D].Wuhan:Changjiang River Scientific Research Institute,2011.(in Chinese)
18 符娜,李闯,刘艳伟,等.基于灌溉需求指数的滇中地区烤烟需水量时空变化分析[J/OL].农业机械学报,2016,47(4):155-161.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160421&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2016.04.021. FU Na,LI Chuang,LIU Yanwei,et al.Temporal and spatial variation analysis of water requirement of tobacco in middle of Yunnan Province based on irrigation requirement index[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2016,47(4):155-161.(in Chinese)
19 MAKKINK G F.Testing the Penman formula by means of lysimeters[J].Jinst Water Engineers,1957,11(3):277-288.
20 PENMAN H L.Natural evaporation from open water,bare soil and grass[J].Proceedings of the Royal Society A,1948,193:120-146.
21 DOUGLAS E M,JACOBS J M,SUMNER D M,et al.A comparison of models for estimating potential evapotranspiration for Florida land cover types[J].Journal of Hydrology,2009,373(3-4):366-376.
22 TRAJKOVIC S.Evaluation of reference evapotranspiration equations under humid conditions[J].Waters Resource Management,2009,23(14):3057-3067.
23 HAUSER V L,GIMON D M,HORIN J D.Draft protocol for controlling contaminated groundwater by phytostabilization[R].Prepared for Air Force Center for Environmental Excellence Technology Transfer Division,1999,11.
24 胡增运,倪勇勇,邵华,等.CFSR、ERA-Interim和MERRA降水资料在中亚地区的适用性[J].干旱区地理,2013,36(4):700-708. HU Zengyun,NI Yongyong,SHAO Hua,et al.Applicability study of CFSR, ERA-Interim and MERRA precipitation estimates in Central Asia[J].Arid Land Geography,2013,36(4):700-708.(in Chinese)
25 虞连玉,蔡焕杰,姚付启,等.植被指数反演冬小麦植被覆盖度的适用性研究[J/OL].农业机械学报,2015,46(1):231-239.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150133 &journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.01.033. YU Lianyu,CAI Huanjie,YAO Fuqi,et al.Applicability of vegetation indices to estimate fractional vegetation coverage[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2015,46(1):231-239.(in Chinese)
26 卫新东,刘守阳,陈滇豫,等.Shuttleworth-Wallace模型模拟陕北枣林蒸散适用性分析[J/OL].农业机械学报,2015,46(3):142-151.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20150320&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2015.03.020. WEI Xindong,LIU Shouyang,CHEN Dianyu,et al.Applicability of Shuttleworth-Wallace model for evapotranspiration estimation of jujube forests in Loess hilly-gully region[J/OL].Transactions of the Chinese Society for Agricultural Machinery,2015,46(3):142-151.(in Chinese)
27 KISI O.Comparison of different empirical methods forestimating daily reference evapotranspiration in mediterranean climate[J].Journal of Irrigation and Drainage Engineering,2014,140(1):336-347.
28 杜加强,熊珊珊,刘成程,等.黄河上游地区几种参考作物蒸散量计算方法的适用性比较[J].干旱区地理,2013,36(5):831-840. DU Jiaqiang,XIONG Shanshan,LIU Chengcheng,et al.Comparison of models for estimating reference crop evapotranspiration in the headwater catchment of the Yellow River basin,China[J].Arid Land Geography,2013,36(5):831-840.(in Chinese)
29 WEIB M,MENZEL L.A global comparison of four potential evapotranspiration equations and their relevance to stream flow modeling in semi-arid environments[J].Advances in Geosciences,2008,18:15-23.
Adaptation Evaluation for Reference Evapotranspiration Calculation Methods in Different Eco-hydrological Regionalization of Yunnan Province
FU Na1SONG Xiaoyu1XIA Lu1LI Lanjun1MENG Chunfang1,2
(1.StateKeyLaboratoryofEco-hydraulicEngineeringinAridArea,Xi’anUniversityofTechnology,Xi’an710048,China2.XinxiangHydrologyandWaterResourcesSurveyBureau,Xinxiang453000,China)
Adaptation evaluation for reference evapotranspiration (ET0) methods can obtain simplified calculation methods ofET0under the conditions of lacking meteorological data and increase the accuracy with the lack of meteorological data in the large area. To obtain the best calculation methods and assess its adaptability, Yunnan Province was divided into three regions, including the mountain plateau and high mountain water abundance region in western and southwestern of Yunnan (Ⅰ), the mountain plateau and river valley water middle region in northwestern and northeastern of Yunnan (Ⅱ) and the plateau water middle and shortage region in central and northern of Yunnan (Ⅲ), and the dailyET0was calculated in 36 stations from 1958 to 2013. Ten kinds of methods, such as FAO 56 Penman-Monteith, Hargreaves-Samani, Irmark-Allen, Pristley-Taylor, Makkink, 1948 Penman, Penman-Van Bavel, Turc, FAO 24 Radiation and Jensen-Haise, were used to calculate the dailyET0of each station of Yunnan Province. Penman-Monteith method was used as the standard method to calculate the dailyET0because of its accuracy, and the precision of other methods was evaluated by the linear regression coefficient, the daily relative root mean square error, the mean bias error and the coefficient of Nash-Sutcliffe. The results showed that 1948-Penman method had the strongest applicability and the highest calculation accuracy, and Radiation FAO 24 method and Jensen-Haise method had large error. Among all the methods, Hargreaves-Samani method was the best one in region Ⅰ, and 1948-Penman method was the most appropriate from January to June while Priestley-Taylor method was the most suitable from July to December of each year for regions Ⅱ and Ⅲ. In the spatial distribution of relative error, the relative error of Hargreaves-Samani method, Irmark-Allen method and Priestley-Taylor method was below 20%, so the three methods were appropriate for region I, and the relative error of Priestley-Taylor method and 1948-Penman method was in the range of 0~20%, as the minimum in regions Ⅱ and Ⅲ, and the relative error of Irmark-Allen method was small in region Ⅱ. When reference crop evapotranspiration was calculated in Yunnan Province, as a consequence, 1948-Penman method was recommended in the whole region, Hargreaves-Saman method was recommended in mountain plateau and high mountain water abundance region in western and southwestern of Yunnan, Priestley-Taylor method was recommended in mountain plateau and river valley water middle region in northwestern and northeastern of Yunnan.
reference evapotranspiration; Yunnan Province; eco-hydrological regionalization; meteorological factors; calculation methods; adaptation evaluation
2016-09-13
2016-10-20
国家自然科学基金项目(51239009、41171034)、陕西省水利科技计划项目(2016slkj-11)和陕西省教育厅省级重点实验室科研计划项目(14JS059)
符娜(1990—),女,博士生,主要从事水文学及水资源研究,E-mail: fnsnow@163.com
宋孝玉(1971—),女,教授,博士生导师,主要从事水文学及水资源研究,E-mail: songxy@xaut.edu.cn
10.6041/j.issn.1000-1298.2017.05.026
S161.4
A
1000-1298(2017)05-0208-10

