基于三次拉格朗日曲线拟合轨迹的斜置式扎穴机构研究

王金武 周文琪 王 秀 李 鑫 王金龙 李树伟

(1.东北农业大学工程学院， 哈尔滨 150030； 2.北京农业智能装备技术研究中心， 北京 100097)

基于三次拉格朗日曲线拟合轨迹的斜置式扎穴机构研究

王金武1周文琪1王 秀2李 鑫1王金龙1李树伟1

(1.东北农业大学工程学院， 哈尔滨 150030； 2.北京农业智能装备技术研究中心， 北京 100097)

为更好地满足斜置式扎穴机构喷肥针的入出土轨迹姿态以及不损伤作物的农艺要求，提出基于三次拉格朗日曲线拟合扎穴轨迹的逆向设计参数优化方法，为得到理想的“杏胡形”扎穴轨迹，通过改变相对轨迹上若干型值点的坐标，控制喷肥针入出土姿态并建立喷肥针的运动学模型，采用Matlab GUI开发平台，编写了斜置式非规则齿轮行星轮系扎穴机构的逆向设计与运动学分析仿真软件，最终得到非规则齿轮行星轮系的节曲线、喷肥针的入出土角及喷肥针尖的速度随行星架转角的变化曲线。通过高速摄影试验，观察和分析了在扎穴机构不同斜置角度下喷肥针尖相对运动轨迹的变化规律。试验结果表明，随着机构斜置角度的增大，喷肥针轨迹横向尺寸不变，纵向尺寸减小，扎穴轨迹段曲线逐渐向里收缩。在保证喷肥针扎入土壤一定深度情况下，喷肥针入出土角逐渐增大，随着机构斜置角度的增大，喷肥针轨迹的穴口宽度逐渐增大。

液态施肥机； 扎穴机构； 运动轨迹； 三次拉格朗日曲线

引言

扎穴深施肥技术是将液肥集中施于土壤耕作层的作物根系附近，有利于加快作物对液肥的吸收，提高作物的产量和质量[1]。因此，研制深施型液态施肥机具对扎穴深施肥技术的大范围推广有着重大的现实意义[2-5]。

东北农业大学研制的深施型液态施肥机核心部件——扎穴机构，采用曲柄摇杆式时，虽然能满足深施液态肥的功能，但其固有运动惯性力和其本身的结构形式使得扎穴次数进一步提高时，振动大大加剧；椭圆齿轮行星系扎穴机构虽然经过运动学和动力学优化，由于仅有一个喷肥针工作，实际扎穴仅为400次/min，进一步提高扎穴次数振动仍会加剧，因此实现不了高速扎穴性能；全椭圆齿轮行星系扎穴机构虽然能实现高速扎穴，但其存在喷肥针入出土垂直度差，导致穴口增大，影响液肥的挥发，造成肥料浪费和环境污染；采用二级传动的非圆齿轮行星轮系扎穴机构[6-8]，虽然喷肥针的入出土垂直角度均有所提高，但齿轮啮合精度较高，很难达到传动特性要求；变形椭圆齿轮式扎穴机构采用5个变形椭圆齿轮组成的驱动轮系[9]，相比上述几种扎穴机构，喷肥针的入出土垂直度均有提高，且变形齿轮啮合精度不高，可满足其传动特性，但由于机构采用正求方法进行设计，对机构进行优化时，此方法具有一定的盲目性，很难找到最佳的优化目标，而且喷肥针扎穴形式为正入式扎穴，对作物损伤较大[10-12]。因此，喷肥针的入出土垂直度与不损伤作物双目标无法兼得。

针对上述问题，本文提出基于三次拉格朗日曲线拟合轨迹的斜置式非规则齿轮行星轮系扎穴机构。采用逆向设计的整体思路[13-15]，避免通过正向设计时运用参数试凑方法得到喷肥针轨迹的盲目性，并充分利用三次拉格朗日曲线拟合特性，以满足喷肥针在入土到出土过程段对轨迹的高精度拟合。

1 斜置式非规则齿轮行星轮系扎穴轨迹和姿态分析

斜置式扎穴机构相对运动轨迹与工作位置如图1所示。以轨迹平面偏向扎穴位置竖直平面20°为例进行说明，喷肥针从E点扎入土壤并从F点拔出，此处形成的轨迹段为扎穴轨迹段。其优化目标为：①为避免垄面上出现较大穴口，喷肥针在扎入与拔出土壤时，其在竖直平面的投影应尽量与垄面呈90°。②为避免喷肥针在垄面上划出一道沟痕，实现高速扎穴，扎穴轨迹段的曲率变化要迅速。③为避免对作物茎叶造成机械损伤，轨迹平面与竖直平面偏置一定角度。因此合理的斜置角度是保证不损伤作物以及满足穴口小的尺寸要求。

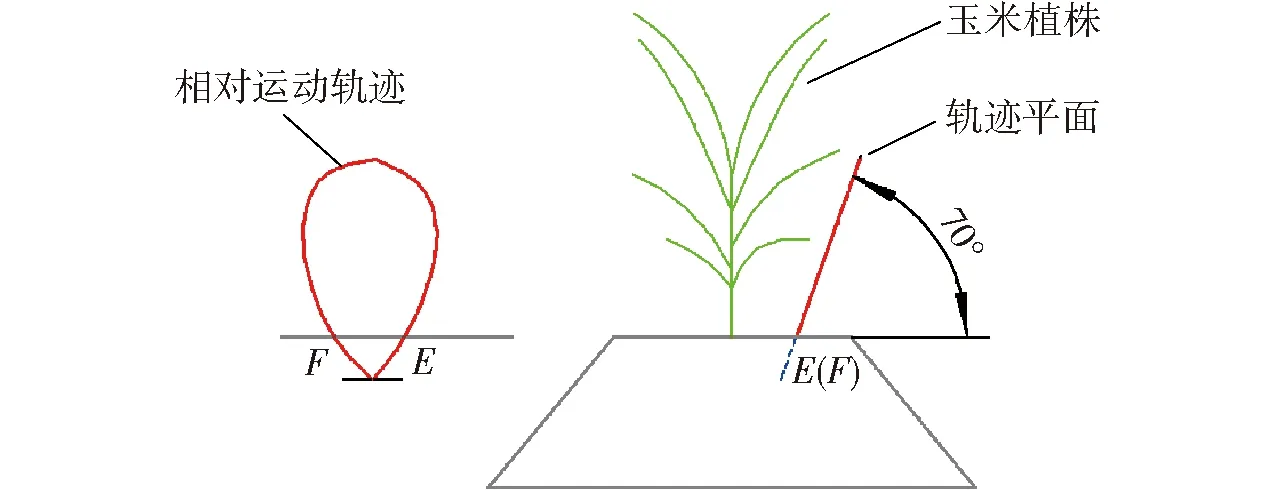
图1 喷肥针“杏胡”形轨迹Fig.1 Trajectory of spray fertilizer needle

2 “杏胡形”轨迹再现算法

获得喷肥针“杏胡形”轨迹上的各个位置坐标是机构逆向设计的基础，其关键在于轨迹曲线的构造需满足曲率连续性和轨迹调整方便的要求。三次拉格朗日曲线拟合特性可以保证曲线上各点的2阶连续性，尤其在扎穴轨迹段拟合精度高，同时通过调整给定的型值点可以方便地控制输出轨迹形状，因此选定此曲线作为封闭轨迹的拟合曲线[16]。

2.1 型值点数量的确定

型值点数量决定方程的求解复杂性，由于拟合的封闭曲线通过型值点，型值点也基本决定了封闭曲线的形状。因此，根据其运动特性选取5个主要型值点控制扎穴轨迹段曲线的形状和变化规律，各个型值点分别为：喷肥针进入垄面时的相对运动轨迹点Q3，喷肥针入土时相对运动轨迹姿态的关键点Q4，轨迹的最低点Q5，喷肥针出土时相对运动轨迹姿态的关键点Q6，喷肥针退出垄面时的相对运动轨迹点Q7。在轨迹空程段(垄面上的轨迹段)，选取其他型值点作为辅助点即可，总体型值点分布图[17]如图2所示。

图2 轨迹型值点布置示意图Fig.2 Sketch of arranging points on static trajectory

2.2 由型值点逆向求解三次拉格朗日曲线的控制点

根据三次拉格朗日曲线求解理论，设定n+1个控制曲线顶点pi(i=0,1,…,n)，同时定义节点矢量U=(u0,u1,…,un+4)。可采用积累弦长参数化求取，其参数的计算式为

(1)

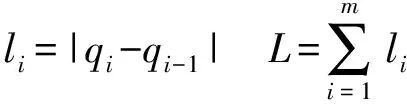
三次拉格朗日曲线方程[14]为

(2)

式中pj——第j个控制顶点Nj,3(u)——在j点处的三次拉格朗日基函数

将定义域u∈[ui,ui+1]⊂[uk,un+1]内的节点值代入式(2)得

(3)

式(3)包含m+1个方程，但首末数据点相重(q0=qm)，方程剩下m=n-2个。首末3个控制顶点相重(p0=pn-2,pn-1=p1,pn=p2)，控制点未知数也剩下n-2个，因此该方程组可解。将式(3)写成矩阵形式，即可求出全部未知点。

2.3 由控制点计算喷肥针尖轨迹

给定控制顶点pi(i=0,1,…,n)、次数k=3及节点矢量U，便可定义一条三次拉格朗日曲线。并给出曲线定义域内一有效参数值区间为u∈[ui,ui+1]⊂[uk,un+1]，即可采用德布尔算法[8]的递推公式求解三次拉格朗日曲线上对应一点p(u)。

(4)

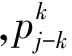
3 喷肥针运动学模型的建立

影响喷肥针斜置式扎穴的驱动部件为非规则齿轮行星轮系，为了方便计算与分析，将其转化为正入式扎穴时的工作状态，如图3所示。根据斜置式扎穴机构的结构特点，建立喷肥针的运动学模型，在此基础上计算出关键点的相对速度及绝对速度方程[19-20]。

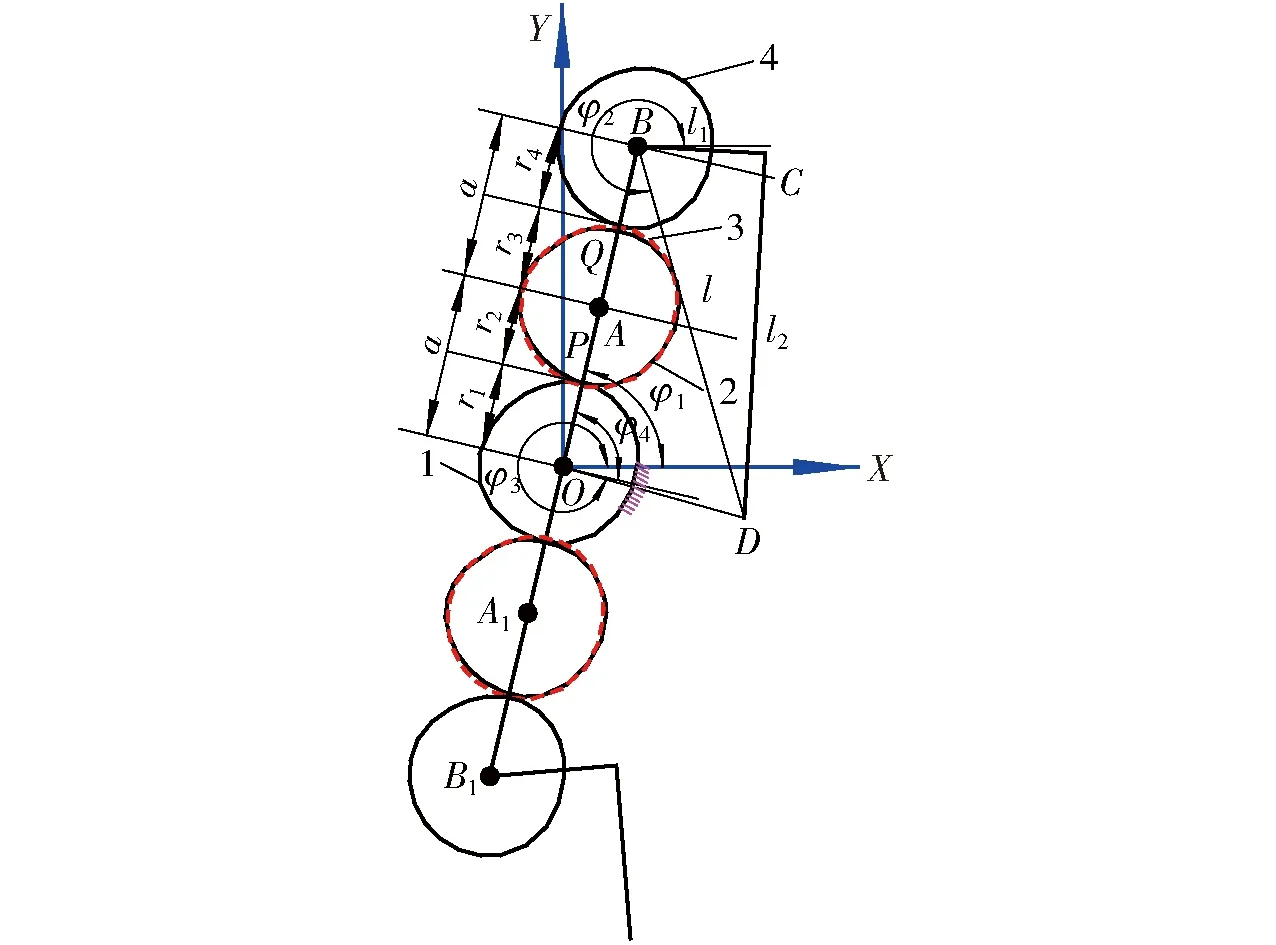
图3 非规则齿轮行星轮系扎穴机构简图Fig.3 Diagram of non-circular planet gear trains pricking hole mechanism1.太阳轮 2.第1级中间轮 3.第2级中间轮 4.行星轮

3.1 相对位移方程

中间轮旋转中心A的相对位移方程为

(5)

式中xA——A点的水平相对位移yA——A点的垂直相对位移φ1——行星架的角位移(大于零)，(°)a——太阳轮与第1级中间轮以及第2级中间轮与行星轮的中心距，mm

行星轮旋转中心B的相对位移方程为

(6)

式中xB——B点的水平相对位移yB——B点的垂直相对位移

喷肥针尖点D的相对位移方程为

(7)

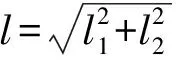
式中xD——D点的水平相对位移yD——D点的垂直相对位移l——行星轮轴心与喷肥针尖点的距离，mmφ2——喷肥针尖点的角位移(大于零)，(°)l1——摇臂长度，mml2——喷肥针长度，mm

因此最终求得斜置式扎穴时的喷肥针尖点相对速度方程为

(8)

3.2 绝对位移方程

中间轮旋转中心A的绝对位移方程为

(9)

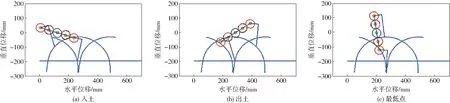
图5 喷肥针扎穴过程中姿态Fig.5 Postures of spray fertilizer needle pricking hole

行星轮旋转中心B的绝对位移方程为

(10)

式中xBa——B点的水平绝对位移yBa——B点的垂直绝对位移

喷肥针尖点D的绝对位移方程为

(11)

式中xDa——D点的水平绝对位移yDa——D点的垂直绝对位移

最终求得斜置式扎穴时的喷肥针尖点绝对速度方程为

(12)

4 扎穴机构运动学仿真

根据前期所建立的非规则齿轮行星轮系扎穴机构逆向求解方法，开发斜置式非规则齿轮行星轮系扎穴机构逆向设计与运动学仿真软件，软件界面如图4所示[11,19]。应用软件的人机交互功能，得到喷肥针入土点、最低点以及出土点的姿态，如图5所示。喷肥针入土角为79.8°，出土角为73°。点击运动学分析模块，得到喷肥针尖点速度随行星架转角的变化规律。从图6分析可获得，喷肥针在入土与出土过程中，行星架转角在133°～229°之间，喷肥针水平速度趋近于零，垂直速度呈递增的规律。在此种情况下，机构的前进速度与喷肥针的水平速度大小几乎相等方向相反，喷肥针无推土和刨土现象发生，此时垄面会达到穴口小的农艺要求。

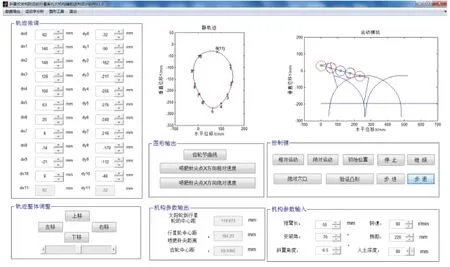
图4 软件主界面Fig.4 Initial interface of software

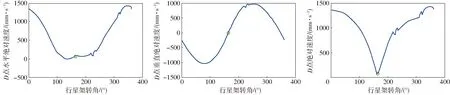
图6 喷肥针尖点速度曲线Fig.6 Speed curve of cusp of spray fertilizer needle

5 喷肥针尖轨迹高速摄像试验

5.1 试验台设计

为得到斜置式扎穴轨迹随斜置角度的变化规律，本文设计高速摄像试验台，并对斜置式非规则齿轮行星轮系扎穴机构喷肥针的相对运动进行拍摄，得到喷肥针的相对运动轨迹,并对其进行分析[21-22]。

如图7所示，斜置式非规则齿轮行星轮系扎穴机构高速摄像试验台主要由高速摄像机(型号为Phantom V5.1，美国Vision Research公司)、强光灯、扎穴装置试验台车(包括变频柜、试验台车、电动机、扎穴机构和传动装置)与计算机等部分组成。其中电动机由变频柜控制(型号为Y90S-4，上海力博电机有限公司)，控制扎穴机构的周转运动，喷肥针固装在扎穴机构的摇臂上，通过非规则齿轮变传动的特性完成喷肥针的相对运动轨迹。图8为图7红色椭圆形区域扎穴机构放大图。

图7 斜置式非规则齿轮行星轮系扎穴机构高速摄像试验台Fig.7 Test-bed of non-circular planetary gear trains pricking hole mechanism for diagonal1.试验台车 2.计算机 3.高速摄像机 4.扎穴机构 5.强光灯

图8 扎穴机构放大图Fig.8 Enlarged image of pricking hole mechanism1.电动机 2.喷肥针

5.2 试验测试及方法

根据田间实际农艺要求，调节试验台行星架转速至75 r/min平稳转动，此时电动机频率为3.8 Hz，试验台车无前进运动。在机构斜置角度为6.5°、20°、33.5°时，通过高速摄像机对其进行图像采集及录制相关视频。运用Phantom V5.1软件的Measurements Angle模块处理相关试验图片及数据，记录喷肥针入土与出土过程中倾斜角及姿态变化。

5.3 试验结果与分析

喷肥针在不同斜置角度时，相对运动轨迹形态如图9所示。随斜置角度的变大，轨迹纵向尺寸减小，横向尺寸不变，喷肥针扎穴轨迹段逐渐向内收缩，实际测得轨迹与理论得到轨迹相同。因此在保证扎穴一定深度的情况下，随着斜置角度的改变，喷肥针入、出土姿态和轨迹不相同。

喷肥针在扎穴过程中，随着机构斜置角度的增大，喷肥针入土角度逐渐减小，实际测得角度分别为79.6°、78.3°和77.4°；喷肥针出土角度逐渐减小，实际测得角度分别为78.2°、75.7°和69.8°。上述入出土角度与理论分析一致，验证了该种方法的合理性。经分析可得到，随着机构斜置角度增大，为保证一定扎穴深度，喷肥针需提前入土，因此在入土到最低点过程中，喷肥针前倾角度较大且时间较长；同理分析，在最低点到出土过程中，喷肥针后仰角度也较大且时间较长，因此在实际作业过程中，喷肥针出现向前推土与向后抛土现象，即垄面上穴口逐渐变大。

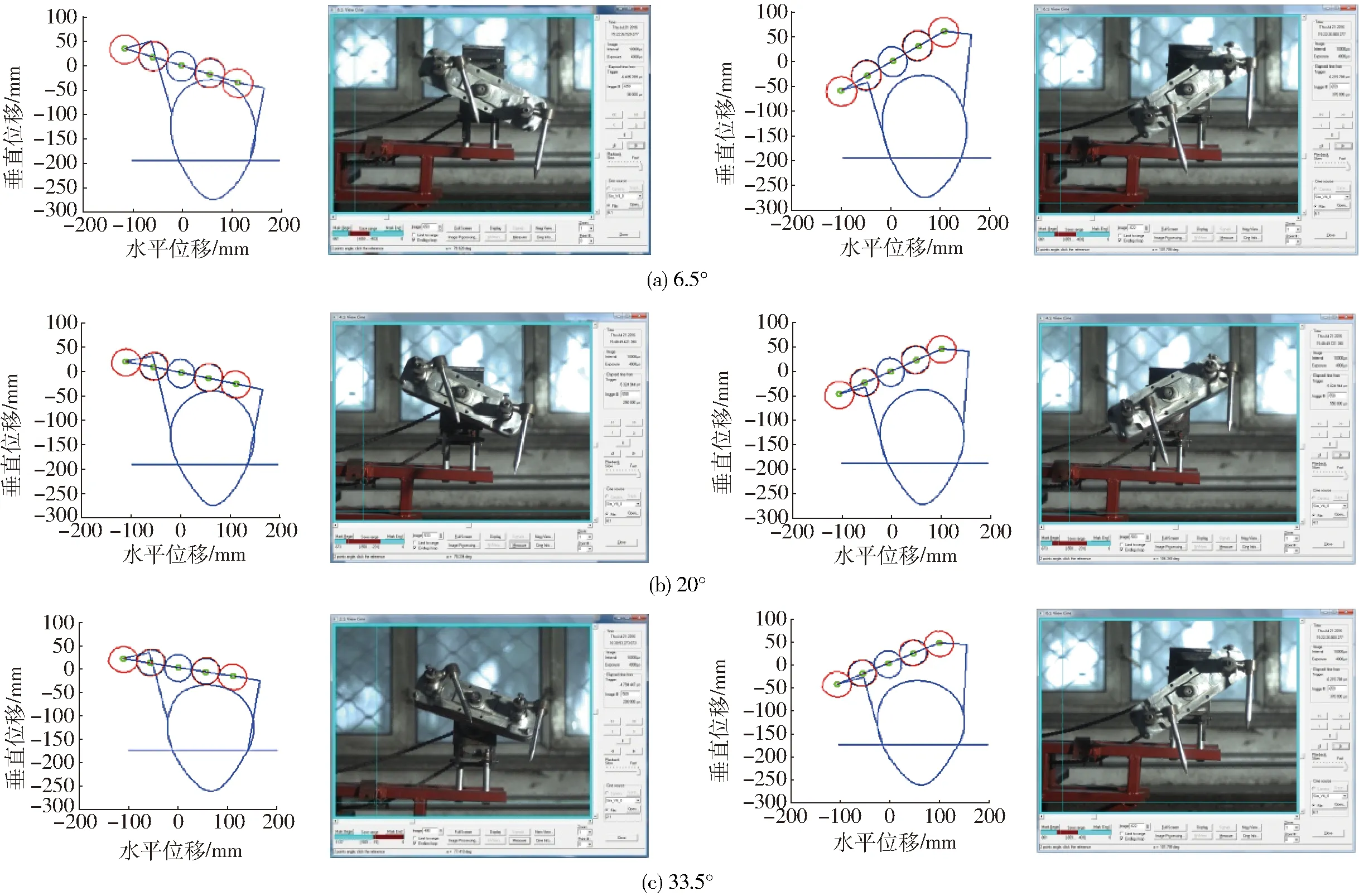
图9 喷肥针尖相对运动轨迹Fig.9 Relative motion tracks of spray fertilizer needle point

6 结论

(1)根据斜置式扎穴轨迹的姿态要求，通过三次拉格朗日曲线拟合方法拟合相对运动轨迹，利用逆向求解方法，编写扎穴机构运动学仿真分析软件，获得喷肥针入土点、最低点以及出土点的姿态变化，并形成“杏胡形”喷肥针的运动轨迹。

(2)建立喷肥针的运动学模型，通过解析法获得斜置式喷肥针尖点的相对速度与绝对速度方程。

(3)对扎穴机构在不同斜置角度下，进行高速摄像试验，分析喷肥针斜置式扎穴的轨迹姿态动态变化规律。结果表明，随着机构斜置角度的增大，喷肥针入、出土角度逐渐减小，实际测得入土角度分别为79.6°、78.3°和77.4°，出土角度分别为78.2°、75.7°和69.8°。验证了应用三次拉格朗日曲线拟合方法得到的扎穴机构轨迹可满足喷肥针斜置式扎穴的要求。

1 张义峰，杨景波，衣淑娟.牧草免耕播种与液体施肥机的设计[J].黑龙江八一农垦大学学报，2011，23(4)：20-22. ZHANG Yifeng, YANG Jingbo, YI Shujuan. Design on machine of fodder grass zero tillage seeding and liquid apply fertilizer[J]. Journal of Heilongjiang Bayi Agricultural University,2011,23(4):20-22.(in Chinese)

地质雷达接收信号通过转换处理后传送到计算机端接收处，再通过对应的数据处理（如零点调整、减背景、增益）后形成雷达探测图像。只要探测物与周围介质存在介电常数差异，图像就会显示出异常，并根据同相轴追踪得到探测物反射波的旅行时长T，由公式（1）便能得出目的层所在的深度：

2 王云霞.液体肥料的应用现状与发展趋势[J].化肥设计，2003，41(4)：10-13.

3 徐秀成．提高肥料利用率化工部门能做些什么[J]．磷肥与复肥，1999，14(3)：6-11. XU Xiucheng. What can departments of chemical industry do for raising fertilizer use efficiency [J]. Phosphate & Compound Fertilizer,1999,14(3):6-11.(in Chinese)

4 窦桂梅，刘巧英．机械深施化肥应用技术研究[J]．山西农业科学，2000，28(2)：56-58． DOU Guimei, LIU Qiaoying. Research on application technology of mechanized deep fertilization[J]. Agricultural Science of Shanxi, 2000,28(2):56-58.(in Chinese)

5 李伟，李絮花，李海燕，等.控释尿素与普通尿素混施对夏玉米产量和氮肥效率的影响[J].作物学报，2012,38(4):700-709. LI Wei, LI Xuhua, LI Haiyan, et al. Effect of different mixing rates of controlled-release urea and common urea on grain yield and nitrogen use efficiency of summer maize [J]. Acta Agronomica Sinica,2012,38(4):700-709.(in Chinese)

6 王金武，周文琪，张春凤，等. 非规则齿轮行星系扎穴机构反求设计与试验[J/OL].农业机械学报，2015，46(11):71-75. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20151111&journal_id=jcsam.DOI: 10.6041/j.issn.1000-1298.2015.11.011. WANG Jinwu，ZHOU Wenqi，ZHANG Chunfeng，et al. Reverse design and experiment of non-circular gear planetary system picking hole mechanism [J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2015,46(11):71-75.(in Chinese)

7 刘春香，王金武，周文琪，等.液肥深施双斜孔式喷肥针动力学分析与试验[J/OL].农业机械学报，2016，47(3):54-58. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_ no=20160308& journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2016.03.008. LIU Chunxiang， WANG Jinwu， ZHOU Wenqi, et al. Dynamics analysis and experiment of double oblique hole spray fertilizer needle of liquid fertilizer deep-fertilization[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2016,47(3):54-58.(in Chinese)

8 刘春香，王金武，唐汉，等.基于贝塞尔曲线的液肥扎穴机构动力学分析与试验[J/OL].农业机械学报，2016，47(5)：116-122. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20160516&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2016.05.016. LIU Chunxiang，WANG Jinwu，TANG Han, et al. Dynamics analysis and test on picking hole mechanism of liquid fertilizer based on bezier curve[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2016,47(5):116-122. (in Chinese)

9 冯金龙，王金武，周文琪，等. 变形椭圆齿轮式扎穴机构设计与工作参数试验优化[J/OL]. 农业机械学报，2017，48(4)：1-8.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20170411&journal_id=jcsam.10.6041/j.issn.1000-1298.2017.04.011. FENG Jinlong，WANG Jinwu，ZHOU Wenqi, et al. Design of pricking hole mechanism with deformation elliptical gears and optimization of experiment with work parameters[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017，48(4)：1-8. (in Chinese)

10 何剑南.液肥注射式工作部件的工作机理与试验研究[D].哈尔滨：东北农业大学，2013. HE Jiannan. Study on working principle and experiment of work components of liquid fertilizer injection type[D]. Harbin:Northeast Agricultural University,2013.(in Chinese)

11 陈建能，黄前泽，王英，等.钵苗移栽机非圆齿轮行星轮系栽植机构参数分析与反求[J].农业工程学报，2013，29(8)：18-26. CHEN Jianneng, HUANG Qianze, WANG Ying,et al.Parametric analysis and inversion of transplanting mechanism with planetary non-circular gears for potted-seedling transplanter[J]. Transactions of the CSAE, 2013,29(8):18-26.(in Chinese)

12 王金武，潘振伟，杨欣伦，等.深施型液态施肥机液肥转子式转换器设计与试验[J/OL].农业机械学报，2014，45(10)：110-115．http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20141018&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2014.10.018. WANG Jinwu, PAN Zhenwei, YANG Xinlun, et al. Design and experiment of rotary converter of liquid fertilizer[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2014,45(10):110-115.(in Chinese)

13 王金武，张春凤，周文琪，等.基于MATLAB仿真的非规则齿轮行星系扎穴机构的优化设计[J].农业工程学报，2016，32(3)：22-28. WANG Jinwu, ZHANG Chunfeng, ZHOU Wenqi,et al. Optimization design of non-circular planetary gear trains pricking hole mechanism based on MATLAB[J].Transactions of the CSAE, 2016,32(3):22-28.(in Chinese)

14 YOSHIAKI Yokoyama， KIYOSHI Ogawa．Dynamic characteristic of the noncircular planetary gear mechanisms with nonuniform motion[J]．Bulletin of the JSME，1974，17(103)：149-152.

15 陈修龙，孙德才，王清.基于拉格朗日的冗余驱动并联机构刚体动力学建模[J/OL].农业机械学报，2015，46(12)：329-336. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20151245&journal_id=jcsam. DOI：10.6041/j.issn.1000-1298.2015.12.045. CHEN Xiulong, SUN Decai, WANG Qing. Rigid dynamics modeling of redundant actuation parallel mechanism based on Lagrange method[J/OL]. Transactions of the Chinese Society for Agricultural Machinery,2015,46(12):329-336.(in Chinese)

16 赵雄，陈建能，王英，等.水稻钵苗“D形”静轨迹移栽机构逆向设计与分析[J].农业工程学报，2012，28(8)：92-97. ZHAO Xiong, CHEN Jianneng, WANG Ying,et al. Reverse design and analysis of rice seedling transplanter with D-shape static trajectory[J]. Transactions of the CSAE, 2012, 28(8): 92-97. (in Chinese)

17 张春凤.非圆齿轮行星系扎穴机构的反求设计与仿真[D].哈尔滨：东北农业大学，2014. ZHANG Chunfeng. Reverse design and kinematic analysis of non-circular planetary gear trains pricking hole mechanism[D].Harbin: Northeast Agricultural University,2014. (in Chinese)

18 吴序堂，王贵海．非圆齿轮及非匀速比传动[M].北京：机械工业出版社，1997.

19 俞高红，赵凤芹，武传宇，等.正齿行星轮分插机构的运动特性分析[J].农业机械学报，2004，35(6)：55-57，51. YU Gaohong, ZHAO Fengqin, WU Chuanyu, et al. Analysis of kinematic property of separating-planting mechanism with planetary gears[J]. Transactions of the Chinese Society for Agricultural Machinery,2004,35(6):55-57,51.(in Chinese)

20 黄前泽．钵苗移栽机行星轮系植苗机构关键技术研究及试验[D]．杭州：浙江理工大学，2012． HUANG Qianze. Study on key technology and test of transplanting mechanism with planetary gears for potted-seeding transplanter[D].Hangzhou:Zhejiang Sci-Tech University,2012. (in Chinese)

21 余佳佳，丁幼春，廖宜涛，等.基于高速摄像的气力式油菜精量排种器投种轨迹分析[J].华中农业大学学报，2014，33(3):103-108. YU Jiajia, DING Youchun, LIAO Yitao,et al. High-speed photography analysis of dropping trajectory on pneumatic metering device for rapeseed[J]. Journal of Huazhong Agricultural University，2014，33(3):103-108. (in Chinese)

22 陶桂香，衣淑娟，汪春，等.基于高速摄像技术的水稻钵盘精量播种装置投种过程分析[J].农业工程学报，2012，28(2)：197-201. TAO Guixiang, YI Shujuan, WANG Chun, et al. Analysis on dropping processing of precision sowing device in rice seeding bowl by high-speed photography[J].Transactions of the CSAE, 2012,28(2):197-201.(in Chinese)

Oblique Type Pricking Hole Mechanism Based on Lagrange Curve for Cubic Fitting Trajectory

WANG Jinwu1ZHOU Wenqi1WANG Xiu2LI Xin1WANG Jinlong1LI Shuwei1
(1.CollegeofEngineering,NortheastAgriculturalUniversity,Harbin150030,China2.BeijingResearchCenterforIntelligentAgriculturalEquipment,Beijing100097,China)

The effects of liquid fertilization for concentrating near crop root system are to speed up the absorption of crops and improve the yield and quality of crops. Deep-into type liquid fertilizer applicator makes the liquid fertilizer into the soil. Aiming to meet the agronomic requirement of trajectory and posture of spray fertilizer needle of oblique type pricking hole mechanism when it got into and out soil and spray fertilizer needle did not damage crops, an optimization method of parameters reverse design was put forward based on Lagrange curve for cubic fitting trajectory. In order to obtain the ideal “xing hu” shaped trajectory for pricking hole, the posture of spray fertilizer needle got into and out soil was controlled by changing the coordinates for some types of value points on static trajectory, and then the kinematics model of spray fertilizer needle was established. The simulation software of reverse design and kinematics analysis was compiled, which was written by Matlab GUI development platform. Finally, the pitch curve of non-circular planetary gear trains, the angle of spray fertilizer needle got into and out soil and speed curve of spray fertilizer needle point along with the change of planet frame angle were got. High-speed photography bench was established and tested. The regulars of relative motion trajectory and absolute motion trajectory of spray fertilizer needle in different oblique angles of pricking hole mechanism were observed and analyzed. The results showed that as the oblique angles of institution increased, the lateral size of track of spray fertilizer needle remained the same, the longitudinal size of track of spray fertilizer needle was decreased, the trajectory curve of pricking hole mechanism was gradually inward contraction. The angles of spray fertilizer needle got into and out the soil were increased gradually when the soil depth was certain; as the oblique angles of institution increased, the width of hole mouth was increased.

liquid fertilizer applicator； pricking hole mechanism； moving trajectory； Lagrange curve for cubic

2016-09-06

2016-09-29

国家自然科学基金项目(51675093)和黑龙江省教育厅科学技术研究项目(12531025)

王金武(1968—)，男，教授，博士生导师，主要从事田间机械和机械可靠性研究，E-mail: jinwuw@163.com

10.6041/j.issn.1000-1298.2017.05.009

S224.21

A

1000-1298(2017)05-0079-07