基于并行离散群居蜘蛛优化算法和压缩感知的WSNs稀疏事件检测

余晓兰，徐跃进，周战馨

(1.重庆城市职业学院，重庆永川 402160; 2重庆大学，重庆 400044；3.常州大学，江苏常州 213000)

工程与应用

基于并行离散群居蜘蛛优化算法和压缩感知的WSNs稀疏事件检测

余晓兰1，徐跃进2，周战馨3

(1.重庆城市职业学院，重庆永川 402160; 2重庆大学，重庆 400044；3.常州大学，江苏常州 213000)

对无线传感器网络(WSNs)弱稀疏性事件检测问题进行研究，提出了一种基于并行离散群居蜘蛛优化算法和压缩感知的WSNs稀疏事件检测方案。该方案采用压缩感知(CS)技术进行稀疏事件分析检测，针对事件向量稀疏度未知的特性，设计基于MPI框架的并行离散群居蜘蛛优化算法(PDSSO)，重新定义蜘蛛编码方式和自适应迭代进化机制，给出并行转移策略，并将PDSSO应用于CS重构算法中；针对观测字典难以满足约束等距条件的特点，对稀疏矩阵和测量矩阵进行奇异值预处理操作，在保持稀疏度不变的基础上提高了算法重构性能。仿真结果表明，与GMP等检测方法相比，该方案有效提高了WSNs稀疏事件检测成功率，降低了误检率和漏检率。

无线传感器网络；稀疏事件检测；压缩感知；离散群居蜘蛛优化算法；并行处理

0 引 言

无线传感器网络(WSNs)稀疏事件检测作为WSNs重要应用之一[1]，已经被成功应用于森林火灾预警、危险化学物质泄漏监测、城市消防等领域[2]。对于大规模WSNs，往往只有少部分传感器节点处于工作状态，以达到降低网络能耗、延长网络寿命的目的。因此，如何利用有限的网络节点实现高质量的稀疏事件检测已经成为当前研究热点[3]。

学者Donoho等[4]在2006年提出的压缩感知(CS)理论通过系列非线性优化算法，能够从少量观测值中实现原始信号的精确重构。同传统信号处理方式不同，CS理论只需要采集少量测量数据，符合WSNs稀疏事件检测要求，为稀疏事件检测提供了全新的研究思路。李鹏等[5]提出了一种基于压缩感知和GM(1,1)的异常事件检测方案，该方案不需要了解异常事件分布先验知识，而且一定程度降低了网络能耗；Xia等[6]构建了l1范数最小化问题求解模型，通过采用OMP算法和自适应修正技术实现了异常事件检测判定；Sun等[7]将故障节点读数恢复问题等效为鲁棒均值计算问题，并提出了定点迭代算法，提高了异常事件检测方案鲁棒计。然而由于WSNs常常部署在恶劣环境，而且受到节点能量有限等因素影响，目前的稀疏事件检测方法还难以很好的应用于实际环境中。

信号重构算法是CS理论关键技术之一，其很大程度的决定了原始信号重构精度[8]，凸优化、组合优化和贪婪迭代是常见的重构算法，但是大多数重构算法需要稀疏度已知等先验知识，此外，观测字典约束等距条件(Restricted Isometry Property，RIP)判定也是CS理论亟需深入研究解决的问题[9]，为此，针对无线传感器网络弱稀疏性事件检测问题，提出了一种基于并行离散群居蜘蛛优化算法和压缩感知的WSNs稀疏事件检测方案，主要做了以下几方面工作：

(1)设计基于MPI框架的并行离散群居蜘蛛优化算法(PDSSO)，创新性重新定义蜘蛛编码方式，给出自适应迭代进化机制和适用于MPI框架下的并行转移策略，明显改善了算法求解离散优化问题的性能。

(2)对CS重构算法改进方法进行研究，将PDSSO应用于CS重构算法中，实现了对稀疏度未知信号的精确重构。

(3)构建WSNs稀疏事件检测模型，设计构造稀疏矩阵和测量矩阵，并对其进行奇异值预处理操作，在满足RIP条件的同时确保了数据稀疏度不变，从而进一步度提高了原始信号重构结果精度，最后通过仿真实验以验证该方案的有效性。

1 问题描述

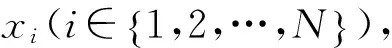
图1 WSNs稀疏事件检测模型

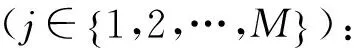
(1)

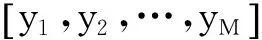
(2)

当M≪N时，式(2)为欠定方程组，其求解过程实质为利用少量测量信号实现稀疏信号逼近[10]，此时可以采用压缩感知技术进行稀疏信号精确重构，从而实现WSNs稀疏事件检测。

2 并行离散群居蜘蛛优化算法与CS重构算法

2.1 离散群居蜘蛛优化算法

Cuevas等[11]通过模拟蜘蛛生物学行为，提出了一种新的智能优化算法：群居蜘蛛优化算法(SocialSpiderOptimizationAlgorithm，SSO)，SSO算法将蜘蛛网等效为算法搜索空间，蜘蛛个体即为优化问题的解，种群内个体协同进化更新，最终实现寻找最优解的目的(SSO算法)。目前关于SSO算法的研究主要集中于求解连续优化问题，而有关离散群居蜘蛛优化(DSSO)算法的研究则相对较少。结合稀疏向量特性，本文重新定义蜘蛛编码方式，并给出自适应迭代进化机制(以雌性蜘蛛和最小化问题为例)。

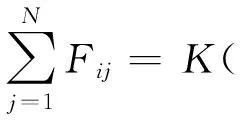
(3)

其中K为正整数，Fij为第j个编码位。

加法算子(⊕) 定义蜘蛛个体Fi与Fj之间加法算子为系列编码置换集合，即：

(4)

从式(4)可以看出任意两个不同的蜘蛛个体可以通过系列编码置换实现相互转换(如图2(b)所示)。

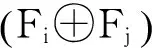
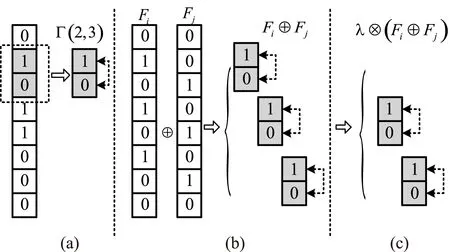
图2 离散蜘蛛编码相关变换

自适应迭代进化机制 对于DSSO算法，其蜘蛛个体Fi迭代更新方式为：

Fi(t+1)=Fi(t)+⎣αμc」⊗(Fi(t)⊕Sc(t))+

⎣βμb」⊗(Fi(t)⊕Sb(t))

(5)

μj=μmin+(μmax-μmin)

(6)

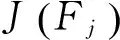
2.2 基于MPI框架的PDSSO算法实现

MPI的提出使得大规模并行计算成为可能。在MPI框架下，并行算法平行运行在局域网内不同PC上，相互之间通过一定互通机制实现信息交流。本文采用基于群体分组的并行离散群居蜘蛛优化算法(PDSSO)，图3给出了PDSSO实现示意图，其中Q个蜘蛛种群同时进行迭代更新操作，每个蜘蛛种群q对应的蜘蛛编码位非零数为Kq(q=1,2,…,Q)。

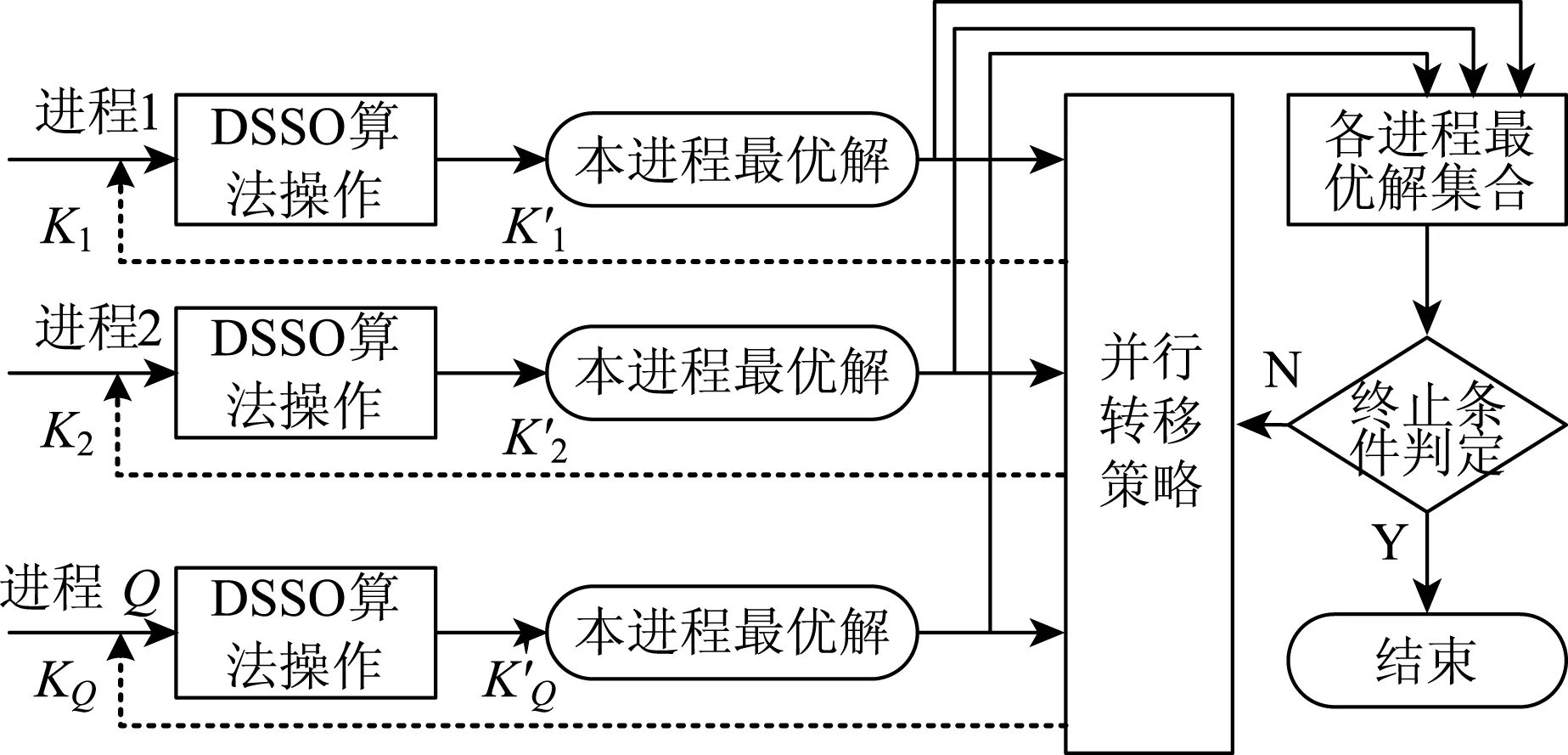
图3 并行离散群居蜘蛛优化算法实现示意图

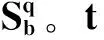
(7)

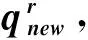
算法运算后期，当所有种群满足式(7)时，进行算法终止条件判断，即有：

(8)

其中，Θ为算法终止控制系数。当有H(H≥2)个种群满足式(8)时，所有种群适应度最好的个体即为目标函数最优解，其对应的Kqs即为最终所要求解的蜘蛛编码位非零数。

2.3 基于PDSSO的CS重构算法

CS理论认为，对于N维信号xN×1，如果存在矩阵ΨN×N，使得xN×1在ΨN×N的线性表示是稀疏的，即：

xN×1=ΨN×NsN×1

(9)

则称ΨN×N为稀疏矩阵，sN×1为xN×1在ΨN×N下的线性表示，并且稀疏度为K(K≪N)。选取一个与ΨN×N非相关的测量矩阵ΦM×N，将xN×1用少量测量数据进行表示，即：

(10)

其中，yM×1为M×1向量测量向量。当M≪N时，式(10)是欠定问题，但是如果观测字典AM×N满足RIP条件，则可以通过l0范数求解实现原始信号恢复，即：

(11)

l0最小范数求解属于NP-hard难题，运算量十分巨大。本文将PDSSO算法应用到CS稀疏重构算法中，将稀疏重构信号等效为蜘蛛个体编码方式，通过多个种群并行进化，以获得稀疏度K和编码非零位置等相关信息，再利用最小二乘法获取非零元素幅度信息，最终实现原始信号重构处理。

目标函数 对于蜘蛛个体Fi，其目标函数定义为：

minJ(si)=‖y-ΦΨsi‖2

(12)

其中，si为蜘蛛个体编码，这里即为稀疏向量sN×1。

基于PDSSO的CS重构算法PDSSORA工作过程可以描述为：

算法初始化。设置ε、Θ以及PDSSO算法相关参数，对蜘蛛种群进行初始化，设置MPI运行环境。

{

Forq=1:Q//对每个蜘蛛种群进行迭代更新

While (t≤Tmax) do

{

蜘蛛种群q内个体执行自适应迭代进化机制。

}

更新种群q最优个体信息。

End for

Q个蜘蛛种群执行并行转移策略。

更新各进程最优解集合。

}

程序结束，输出结果。

3 WSNs稀疏事件检测

3.1 稀疏矩阵与测量矩阵构造

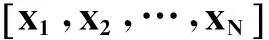
(13)

CS理论认为，利用M个工作节点测量值yM×1就可以恢复原始信号，即：

(14)

3.2 奇异值预处理

虽然观测字典A能够以一定概率满足RIP条件，但是稀疏矩阵Ψ和测量矩阵Φ是相关的，会使得信号稀疏度发生变化，进而影响了原始信号重构结果准确度，为此本文对观测字典A进行奇异值预处理操作，进一步提高了PDSSORA算法重构结果鲁棒性。根据矩阵奇异值分解定理可知，对于观测字典A有：

(15)

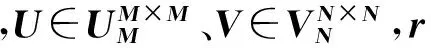
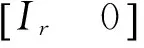
(16)

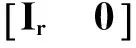
y′=Os

(17)

从式(16)可以看出，矩阵O为VH前r行，并且VH为酉矩阵，所以O行向量相互正交，对O进行单位化处理有：

(18)

从式(17)可以看出，通过单位化矩阵O得到矩阵X，因此X为部分正交矩阵，满足RIP条件，即：

(19)

(20)

从式(20)可以看出，s′与s具有相同的稀疏度，而且没有改变非零编码位置，因此可以采用矩阵X作为CS观测字典，实现稀疏信号精确重构。

4 实验仿真

4.1 实验设置

WSNs监控区域内部署W=400个传感器节点，存在N=100个事件源，选取4台PC机组成局域网，在MPICH并行环境中进行测试。相关参数设置如下：α=0.2、β=0.4、ω0=0.5、Tmax=300，SSO算法参数设置参考文献[13]。评价指标设定为检测成功率Pc和平均相对误差σre：

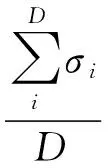
(21)

(22)

其中D为实验次数，σi为第i次试验相对误差，θ为检测成功控制阀值。

4.2 实验结果分析

1.不同检测方案性能对比分析

为进一步分析本文WSNs稀疏事件检测方案PDSSORA的性能，选取基于贪婪匹配跟踪算法(GMP)检测方案和文献[14]提出的基于多次凸优化算法检测方案进行对比实验，每种检测方案重复实验D=100次，图4给出了M=40、稀疏度K未知情况下，PDSSORA和GMP重构信号结果对比。表1给出了稀疏度K取不同数值时，不同检测方案性能对比(M=100)。

图4 PDSSORA和GMP重构信号结果对比(K未知)

从图4可以看出，当K未知时，对于不同稀疏度信号重构，PDSSORA全部实现了非零位置精确定位，而GMP方案随着K的增加，定位效果越来越差，这表明PDSSORA可以完成对K未知原始信号的准确恢复。从表1可以看出，在K确定的情况下，随着K的不断增加，PDSSORA的检测成功率全部为100%，并且平均相对误差要小于其他两种检测算法；而GMP和文献[14]方案的检测成功率逐渐降低，特别的，当K=60时，GMP的Pc已经低于50%。由于采用并行计算模型，PDSSORA运算时间明显快于其他两种方案。

2.并行效率分析

为分析采用MPI框架对PDSSO运算效率影响，分别设置局域网内计算机数量为2台、4台、8台，并与串行算法进行对比。表2给出了PDSSO算法效率结果对比，对比指标为加速比Sp=T1/TP(P、T1和TP分别为局域网内电脑数量、串行算法运算时间和并行算法运算时间)和效率Ep=SP/p。

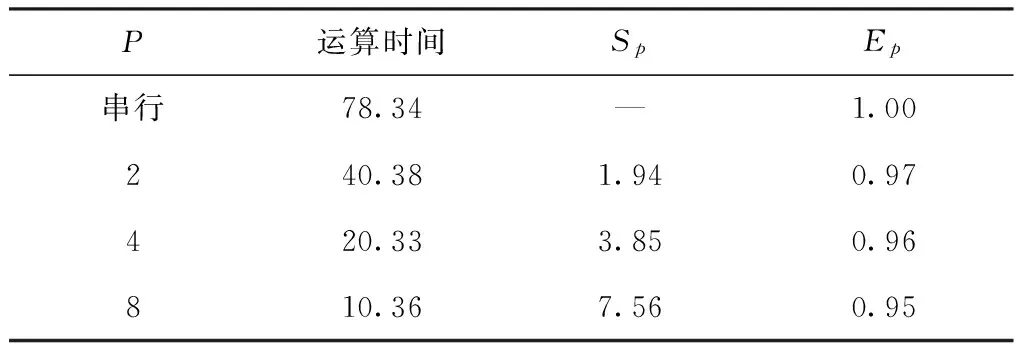
表2 PDSSO算法效率结果对比

从表2可以看出，采用MPI框架能够有效缩短算法计算时间，提高算法运算效率。

3.参数M设置对检测方案性能影响分析

为分析参数设置M对检测方案性能的影响，分别选PDSSORA、GMP和文献[14]方案进行实验。图5给出了设置不同M取值时，三种检测方案对比结果(K未知时)。

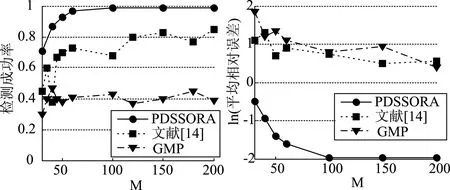
图5 不同M取值3种检测方案性能对比

从图5可以看出，K未知时，随着M不断增加，PDSSORA检测成功率逐渐升高，当M≥100时，Pc≈100%，并且平均相对误差不断减小。而GMP和文献[14]方案的检测成功率波动性较大，都低于85%，并且平均相对误差远远高于PDSSORA，这是因为GMP和文献[14]方案在信号重构过程中需要稀疏度等先验信息，而PDSSORA则可以实现对K未知信号的精确重构。

4.算法抗噪能力分析

为了分析PDSSORA抗噪能力，在测量信号中引入高斯白噪声，分别设置不同SNR取值，并选PDSSORA、GMP和文献[14]方案进行实验(M=80、K=25)。图6给出了不同SNR取值情况下三种检查方案性能对比。

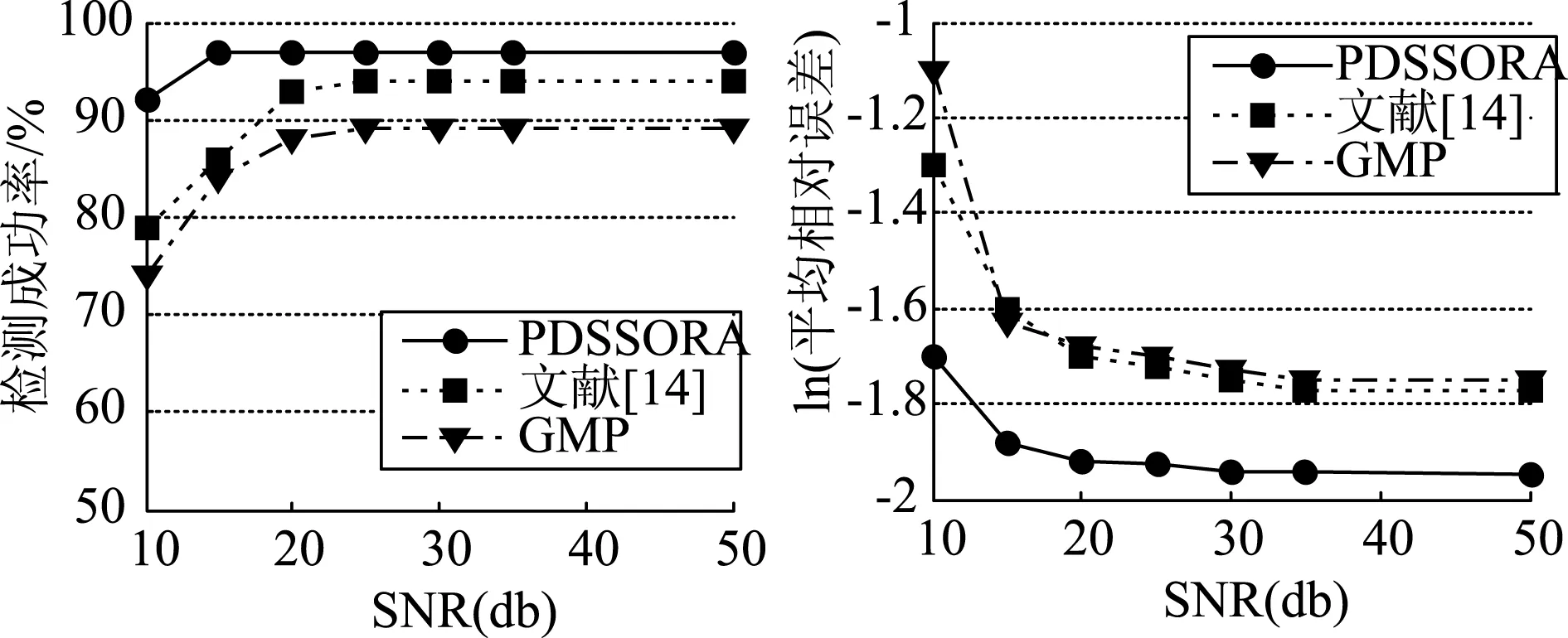
图6 不同SNR取值三种方案性能比较

从图6可以看出，当SNR处于较低水平时，三种算法的检测成功率Pc和平均相对误差σre变化不大；当SNR小于20 dB时，Pc和σre发生了明显变化，但是无论是Pc还是σre，PDSSORA要优于其它两种方案，特别的当SNR取值10 dB时，PDSSORA的Pc仍然可以达到90%以上，这表明PDSSORA具有较强的抗噪声干扰能力。

5 结 语

提出了一种基于并行离散群居蜘蛛优化算法和压缩感知的WSNs稀疏事件检测方案。分别对并行离散群居蜘蛛优化算法实现、CS重构算法改进以及稀疏矩阵与测量矩阵构造问题进行了研究，实现了对稀疏度未知事件向量信号的精确恢复，仿真实验验证了算法的有效性，并且证明了该算法不仅提高了稀疏事件检测成功率，而且具备较强的抗干扰能力。

[1] 李洪成，吴晓平，严博.面向MANET异常检测的分布式遗传k-means研究[J].通信学报，2015，36(11)：167-173.

[2] 刘志新，刘强，袁亚洲，等.基于贝叶斯估计与虚拟力导向混合遗传算法的无线传感网络定位方案[J]. 控制与决策，2013，28(6)：899-903.

[3] 冯立波，罗桂兰，杨存基，等. WSN中基于粒子滤波的入侵检测算法实现[J]. 传感技术学报，2013，26(11)：1573-1578.

[4] D Donoho. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[5] 李鹏，王建新，曹建农.无线传感器网络中基于压缩感知和GM(1,1)的异常检测方案[J].电子与信息学报，2015，37(7)：1586-1590.

[6] Xia Yu, Zhao Zhi-feng, and Zhang Hong-gang. Distributed anomaly event detection in wireless networks using compressed sensing[C]. 2011 11th International Symposium on Communications and Information Technologies, Hangzhou, China, 2011: 250-255.

[7] Sun Bo, Shan Xue-mei, Wu Kui, et al.. Anomaly detection based secure in-network aggregation for wireless sensor networks [J]. IEEE Systems Journal, 2013, 7(1): 13-25.

[8] 张宗念，黄仁泰，闫敬文.压缩感知信号盲稀疏度重构算法[J].电子学报, 2011, 39(1): 18-22.

[9] 周锋，曾雪迎，杨力华.一种基于正则化的稀疏表示方法[J]. 数学学报中文版，2015，58(4)：649-660.

[10]何风行，余志军，刘海涛.基于压缩感知的无线传感器网络多目标定位算法[J]. 电子与信息学报，2012，34(3)：716-721.

[11]Cuevas E, Cienfuegos M. Zaldiva D, et al. A swarm optimization algorithm inspired in the behavior of the social spider [J]. Expert System with Applications, 2013, 40(16):6374-6384.

[12]刘洲洲，王福豹.基于离散萤火虫压缩感知重构的无线传感器网络多目标定位[J].光学精密工程，2014，22(7)：1904-1911.

[13]王艳娇，李晓杰，肖婧.基于动态学习策略的群集蜘蛛优化算法[J].控制与决策，2015，30(9)：1575-1582.

[14]赵秀兰，李克清.弱稀疏性下的无线传感器网络事件检测算法[J].计算机应用与软件，2014，31(3)：104-107.

周战馨 (1970—) ，女，吉林人，副教授，博士，研究领域：自组织网络、智能控制等。

Sparse Event Detection Based on Parallel Discrete Social Spider Optimization Algorithm and Compressed Sensing in Wireless Sensor Networks

YU Xiao-lan1, XU Yue-jin2, ZHOU Zhan-xin3

(1.Chongqing City Vocational College, Chongqing yongchuan, China,402160;2.Chongqing University, Chongqing 400044, China;3. Changzhou University, Changzhou, Jiangsu, 213000)

The problem of sparse event detection in wireless sensor networks (WSNs) is studied, and a new sparse event detection scheme based on parallel discrete social spider optimization algorithm and compressed sensing is proposed. Compressed sensing (CS) technology is used for sparse event detection, and the parallel discrete communal spiders optimization algorithm (PDSSO) based on MPI framework is designed in view of the unknown sparse degree of event vector. A new definition of the spider encoding, an adaptive iterative evolution mechanism and a parallel transfer strategy is proposed in PDSSO, for which is introduced to CS reconstruction algorithm. The singular value pretreatment operation is designed for the sparse matrix and measurement matrix in order to keep the sparse degree and improve the performance of reconstruction algorithm. The simulation results show that, compared to GMP and other detection methods, this scheme can effectively improve the WSNs sparse event detection success rate, and reduce the false detection rate and false negative rate.

wireless sensor networks (WSNs); anomaly event detection; compressed censing; social spider optimization algorithm; parallel processing

10.3969/j.issn.1673-5692.2017.01.019

2016-06-09

2016-12-19

全国教育科学规划重点课题(DBC2012039)；重庆市资助课题(113296 )

TP393

A

1673-5692(2017)01-202-07

余晓兰(1981—)，女，重庆人，硕士，讲师，主要研究方向为机器人及自动化、系统开发研究、数据库与信息处理，物联网等；

E-mail：842669898@qq.com

徐跃进(1979—)，男，江西人，硕士，工程师，主要研究方向：汽车控制及自动化等；