“十三五”期间我国卫生总费用预测

国家卫生计生委统计信息中心(100044)

戴明锋 孟 群△

“十三五”期间我国卫生总费用预测

国家卫生计生委统计信息中心(100044)

戴明锋 孟 群△

目的 预测“十三五”期间我国卫生总费用增长情况以及个人卫生支出占卫生总费用的比重。方法 采用ARIMA模型和GM(1,1)模型，根据我国2000-2015年各年卫生总费用数据建立模型，并预测“十三五”期间卫生总费用。结果 所建立的模型能够很好地拟合历史数据，GM(1,1)模型由于受“十二五”期间卫生总费用增长速度快的原因，预测结果有高估趋势。结论 “十三五”期间，卫生总费用继续增长，按照当前的增长速度，到2020年，个人卫生支出占卫生总费用的比重有望下降到25%以下，卫生总费用占GDP的比重将达到7%。

卫生总费用 ARIMA模型 GM(1,1)模型 趋势预测

卫生总费用是一个国家或地区在一定时期内(通常为一年)，为开展卫生服务活动从全社会筹集的卫生资源的货币总额，按来源法核算。它反映在一定经济条件下，政府、社会和居民个人对卫生保健的重视程度和费用负担水平，以及卫生筹资模式的主要特征和卫生筹资的公平性、合理性。测算卫生总费用，可以为政府调整和制定卫生经济政策提供依据，也是评价社会对人群健康的重视程度，是分析保健体制公平与效率的重要依据。自2009我国实施新医改以来，一直将卫生总费用的一些指标纳入到医改监测中。“十三五”期间，随着医改的不断深入，居民健康管理意识不断增强，医疗服务需求的不断增加，卫生总费用也会不断增长，战略规划目标的实现存在着困难与挑战[1]。预测“十三五”期间卫生总费用，对于卫生部门制定规划和决策提供数据支撑。

数据来源与方法

1.数据来源

本研究的卫生总费用数据来源于历年《中国卫生和计划生育年鉴》，《中国卫生总费用研究报告》等资料，本文收集2000-2015年共16年的数据，包括卫生总费用、政府卫生支出、社会卫生支出、个人卫生支出，其中，2015年为初步测算数。

2.方法

总结近年关于卫生总费用预测的研究文献，大都采用ARIMA模型[2-3]或者GM(1，1)模型[4-5]。ARIMA模型适合任何时间序列的短期预测，GM(1,1)适合对含有不确定因素的系统进行预测。我国正处于深化医药卫生体制改革的关键时期，各种卫生筹资政策的出台，对政府、社会以及居民个人卫生支出将产生不同程度的影响，未来卫生筹资结构不会稳定延续原有状态，甚至在个别年份有可能出现重大调整[6]，具有灰色系统的特征，因此本文分别采用ARIMA模型和GM(1,1)模型进行预测。

(1)ARIMA模型

ARIMA模型的基本思想是将预测对象随时间推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列[7]。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。ARIMA(p，d，q)模型表达式为

φ(B)(1-B)dYt=θ(B)et

(1)

式中，φ(B)=1-φ1B-φ2B2-…-φPBP，θ(B)=1-θ1B-θ2B2-…-θqBq

d为差分阶数，p和q分别是平稳序列的自回归和移动平均阶数；φ(B)和θ(B)分别为自回归算子和移动平均算子。

(2)GM(1，1)模型

GM(1，1)模型是灰色系统理论的核心内容之一，它的特点是需要样本少，计算简单，比传统的预测方法具有优越性[8]。基本理论如下：

设x(0)=(x(0)(1),x(0)(2),…,x(0)(n))为原始数列，其1次累加生成数列为

x(1)=(x(1)(1),x(1)(2),…,x(1)(n))

定义x(1)的灰导数为

d(k)=x(0)(k)=x(1)(k)-x(1)(k-1)

令z(1)为数列的邻值生成数列，即

z(1)(k)=αx(1)(k)+(1-α)x(1)(k-1)

于是定义GM(1，1)的灰微分方程模型为

d(k)+az(1)(k)=b，即x(0)(k)+az(1)(k)=b

(2)

(2)式中，x(0)(k)称为灰导数，α称为发展系数，z(1)(k)称为白化背景值，b称为灰作用量。将时期k=2,3,…,n代入(2)式有：

记

于是定义GM(1，1)模型可表示为

Y=Bu

用最小二乘估计得到

(3)

(4)

(5)

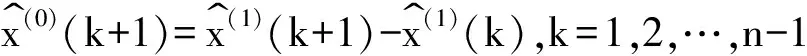
(6)

结 果

1.我国卫生总费用变化趋势

2000-2015年，我国卫生总费用由4586.33亿元增长到40974.64亿元，增长了接近8倍，而同期GDP增长5.8倍，卫生总费用的增长速度高于GDP的增长速度。卫生总费用占GDP的比重由4.6%上升到6.05%。卫生总费用中，政府卫生支出增长16.6倍，社会卫生支出增长13.1倍，个人卫生增长3.4倍，个人卫生支出占卫生总费用比重逐年下降，从2001年最高值59.97%下降到2015年的30%以下。

2.ARIMA模型建立与预测

ARIMA模型的建立需要经过平稳性检验、模型识别、模型定阶、参数估计与诊断，然后根据建立的模型进行预测。

(1)序列的平稳性检验

2000-2015年我国卫生总费用呈增长趋势，需要进行平稳化处理。对数据进行差分处理，使之转化为平稳的时间序列，序列经过两次差分后，表现较为平稳，如图1所示。采用ADF检验，在0.05的检验水准下，差分后的序列平稳。

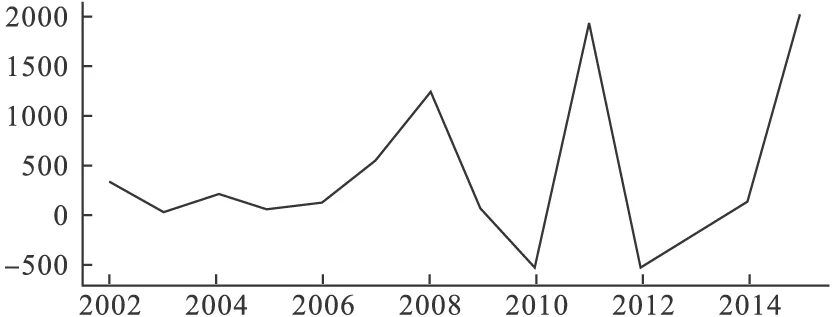
图1 二阶差分后的我国卫生总费用序列图

(2)时间序列模型的识别

根据自相关图和偏自相关图来判断模型的类型。若平稳序列的偏相关函数是截尾的，而自相关函数是拖尾的，可断定序列适合AR模型；若平稳序列的偏相关函数是拖尾的，而自相关函数是截尾的，则可断定序列适合MA模型；若平稳序列的偏相关函数和自相关函数均是拖尾的，则序列适合ARIMA模型。观察图2，自相关系数和偏自相关系数都是拖尾的，所以建立ARIMA模型。

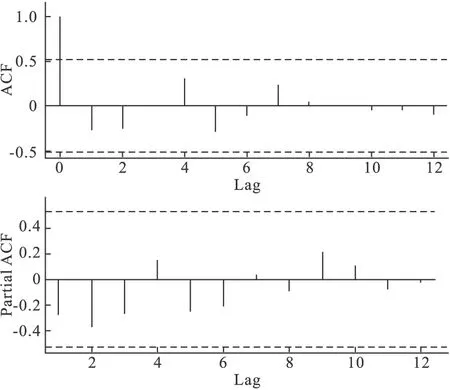
图2 二阶差分后的卫生总费用自相关和偏自相关图

(3)模型的阶数p与q的确定

由图2可以看出，偏自相关系数在滞后两阶后衰减，基本没有超出两个标准差的范围，所以p可以取1或者2，自相关系数在滞后一阶后迅速衰减，所以q可以取1。因此，可以采用ARIMA(1，2，1)或者ARIMA(2，2，1)模型。

(4)模型参数估计与诊断检验

采用极大似然估计法对初选模型ARIMA(1，2，1)和ARIMA(2，2，1)模型检验，结果如表1和2所示。

表1 ARIMA(1，2，1)的估计结果

*：残差平方和 732724:对数似然-114.41,赤池准则 234.83

表2 ARIMA(2，2，1)的估计结果

*：残差平方和 719680:对数似然-114.31,赤池准则 236.62

从模型定阶准则看，ARIMA(1，2，1)和ARIMA(2，2，1)的对数似然、AIC两个指标值都差别不大，但ARIMA(2，2，1)模型的AR(1)和AR(2)参数值小于1，不符合常理，因此选择ARIMA(1，2，1)模型。

(5)ARIMA模型预测

根据建立的模型预测“十三五”期间卫生总费用结果如表3所示。

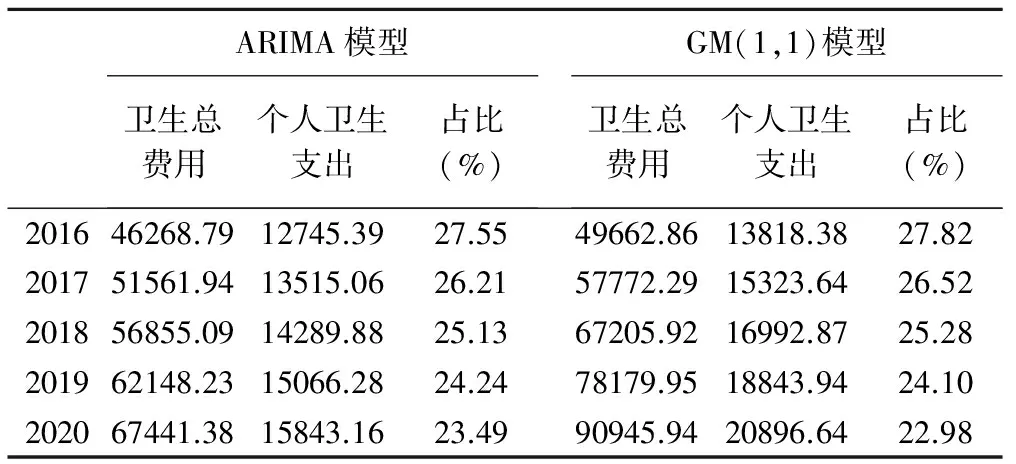
表3 “十三五”期间卫生总费用和个人卫生支出预测结果

3.GM(1,1)模型预测

根据前面GM(1，1)模型的建模思路，得到灰色模型为

x(0)(k)-0.1513x(1)(k)=4064.641

平均相对误差为4.51%，相对精度为95.49%，预测精度较好。绘制预测值与实际值的对比图，如图3所示，可以看出，原始数据和预测数据两条曲线基本重合，所建立的灰色模型能够很好地拟合卫生总费用的变化情况，将模型进行外推，预测“十三五”期间卫生总费用情况如表3所示。

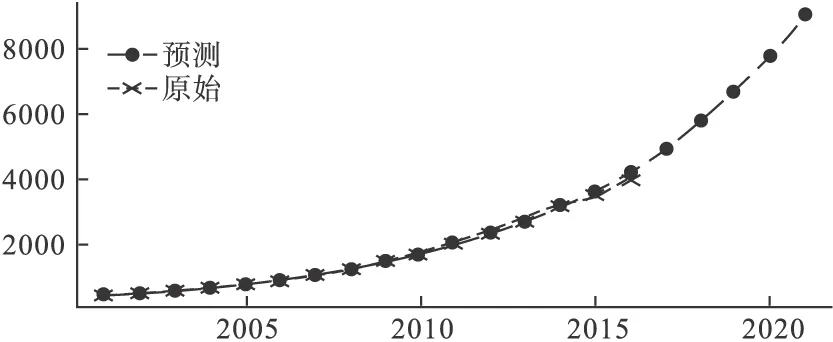
图3 卫生总费用预测值与观测值对比图

4.个人卫生支出预测

为了解个人卫生支出在卫生总费用中的比重，需要预测“十三五”期间个人卫生支出，同样采用ARIMA模型和GM(1,1)模型进行预测，结果见表3。

讨 论

由于收集的资料有限，本文考虑了卫生费用随时间变化自身的变化，没有考虑影响卫生总费用变动的影响因素，预测结果仅作为政策制定的参考，而不能成为决定性的依据。在今后的研究中，需要进一步深化。本文采用ARIMA模型和GM(1，1)模型对“十三五”期间我国卫生总费用进行预测，两种模型都具有比较好的预测结果，GM(1，1)模型由于受“十二五”期间我国卫生总费用增长趋势较快增长的影响，预测结果显著高于ARIMA模型的结果，ARIMA模型不仅考虑了自身变动的影响，还考虑了随机扰动项的影响，所以预测结果更为合理一些。

根据两种模型计算的个人卫生支出占卫生总费用的比重可以看出，按照过去的发展趋势，“十三五”期间个人卫生支出占比持续下降，到2020年有望降到25%以下，居民就医负担有所减轻。根据全面建设小康社会的目标，预计到2020年我国GDP将超过100万亿，如果卫生总费用保持现有的增长速度，到2020年，卫生总费用占GDP的比重将达到7%左右，“十二五”期间，卫生总费用占GDP的比重增长了1个百分点，“十三五”期间，卫生总费用占GDP的比重继续增长一个百分点。

通过模型预测，可以知道“十三五”期间，我国卫生总费用呈增长趋势，根据《“健康中国2030”规划纲要》[9]提出的健全政府健康领域相关投入机制，调整优化财政支出结构，加大健康领域投入力度，科学合理界定中央政府和地方政府支出责任，履行政府保障基本健康服务需求的责任。因此“十三五”期间，在卫生总费用不断增长的情况下，要加强卫生总费用的控制，优化布局，调整结构，加强动态监管。

[1]万泉，张毓辉，翟铁民，等.基于“十二五”卫生事业发展目标我国卫生总费用预测分析.中国卫生经济，2013,32(6)：27-29

[2]陈沛军,黎东生.基于ARIMA模型的中国卫生总费用预测分析.医学与社会,2016,3:18-20.

[3]郑骥飞,尹文强,于倩倩，等.基于ARIMA模型的“十三五”期间卫生总费用趋势预测.中国卫生统计,2016,33(5):823-825.

[4]相静,孔杨,徐天和.基于灰色系统GM(1,1)模型的山东省卫生总费用预测研究.中国卫生统计,2016,33(4):653-656.

[5]许建强,郑娟,井淇,等.深化医改关键时期我国卫生总费用构成预测分析.中国卫生经济,2015,34(4):43-46.

[6]赵郁馨，谢小平，翟铁民.2007年中国卫生总费用分析与预测.中国卫生经济，2009,28(4):14-18.

[7]数据分析与EViews应用.北京：中国人民大学出版社，2014:121-128.

[8]张彬，西桂权.基于背景值和边值修订的GM(1,1)模型优化.系统工程理论与实践，2013，33(3)：836-838.

[9]《“健康中国2030”规划纲要》2016-10-25.http://news.xinhuanet.com/health/2016-10/25/c_1119786029.htm.

(责任编辑：郭海强)

△ 通信作者：孟群，E-mail:mengq@nhfpc.gov.cn