样本量及抽样过程对线性模型中自变量重要性估计方法的影响研究*
伍立志 贾孝霞 沈其君
样本量及抽样过程对线性模型中自变量重要性估计方法的影响研究*
伍立志1贾孝霞2沈其君3△
目的 通过从同一总体中抽样产生不同样本量及相同样本量的重复抽样数据集,来观察并评价样本量对重要性估计方法的影响以及重复抽样过程对各方法估计稳定性的影响。方法 简单介绍已有的几种重要性评价方法,调用SAS中的PROC SURVEYSELECT 过程从同一总体中重复抽样,观察样本量变化、重复抽样过程对重要性估计结果的影响,评价各方法的稳定性。结果 样本量较小时,各方法的重要性估计值变异较大,随着样本量增大估计值也逐渐趋于稳定。优势分析、相对权重、乘积尺度(βr)的重要性估计值之和与模型R2之差,小于标准回归系数平方(β2)、简单相关系数平方(R2),优势分析法的稳定性最好。结论 在现有的几种常见重要性估计方法中,优势分析法的重要性估计稳定性最好,相对权重法虽然与优势分析法最为接近,但仍有不足之处。
线性模型 相对重要性 样本量 抽样过程 模拟研究
线性模型是在卫生、环境调查等领域中常用的一种数据分析方法,如何分析和解释线性模型中自变量对因变量变异的贡献,估计各自变量的相对重要性一直是研究者关注并争论的话题,先后有数量众多的评价方法被提出并推广应用[1-2]。当研究中自变量之间相互独立时,可以应用标准回归系数、Pearson相关系数以及偏相关和半偏相关系数等指标。如果自变量之间互相存在关联时,自变量相对重要性估计变得较为复杂,以上几种指标已不再适用[3]。目前多数学者推荐的估计方法为乘积尺度法、优势分析法和相对权重等方法。本次研究通过模拟随机抽样数据样本,并调用SAS中的PROC SURVEYSELECT 过程从同一总体中重复抽样,观察样本量变化、重复抽样过程对重要性估计结果的影响,将学者推荐的这几种方法与传统的相关系数平方和标准回归系数平方进行比较,评价各方法的稳定性。
自变量相对重要性估计方法简介
1.乘积尺度法
Hoffman于1960年指出模型中自变量(x)的标准回归系数(βx)与相应的简单相关系数(rxy),两者之积和即为决定系数R2,对应的以其乘积βxrxy为每一自变量对因变量变异的贡献,Hoffman的这一方法被Bring等人命名为“乘积尺度”(product measure)[4]。这一方法明显的缺点就是存在自变量实际对因变量变异有贡献时却出现0值或负值等无法解释的情况。
2.优势分析
1993年,Budescu首次提出了“优势分析”这一方法,对于任意两个自变量xi和xj,相对于余下p-2个自变量的任意子集xh,xi均能取得比xj更大的半偏相关系数平方,则称xi对xj具有“优势”[5],Azen和Budescu在2003年修订了“优势”这一定义。将优势分析方法分为完全优势分析、条件优势分析和一般优势分析[6],本文采用了一般优势分析的方法和定义来估计各自变量的相对重要性[7]。
3.相对权重
Johnson提出了ε法即相对权重。它是将自变量Xj正交转换得到的正交变量ZK,以因变量Y对Zk做回归得到回归系数βk,每个自变量Xj分别对Zk做回归得到回归系数λjk。要计算每个自变量的相对重要性,只需计算每个自变量对应两组回归系数的积和ε[8]。公式如下:
(1)

参数设置及实验过程
为考察样本量变化时对各重要性方法的影响,使用同一相关阵通过前述过程生成不同样本量的模拟样本,分别使用不同方法进行自变量相对重要性估计,观测不同方法的估计结果差异。而在考察抽样过程的影响时,先模拟一个样本量为10000的数据集作为抽样所用的总体,抽样过程调用SAS中的PROC SURVEYSELECT 过程,样本量大小100。研究所用的总体相关结构如下表所示:

表1 总体相关阵
生成模拟数据
Kaiser等人在1962年[11]提出一个矩阵分解过程,证明了将一个特定的矩阵左乘一个完全独立随机正态矩阵时,等价于从这一特定矩阵所代表的总体中进行随机抽样的过程。其基本过程如下:
(2)
结 果
1.不同样本量对各方法重要性指标的影响
为考察样本量变化时对各重要性方法的影响,使用同一相关阵通过前述过程生成不同样本量的模拟样本,分别使用不同方法进行自变量相对重要性估计,观测不同方法的估计结果差异。本文所用的总体相关阵如下表所示:

表2 总体相关阵
各自变量重要性估计值之和应该等于总模型的R2,这是在评价自变量重要性估计方法时的一条重要准则[13],因此本文计算了各模拟样本中各方法重要性估计值之和,将变量重要性指标和与R2之差的绝对值作为评价各方法估计偏差的统计量,如下表所列:

表3 各方法的重要性指标之和与模型R2之偏差
样本量设置为从100到10000逐级增加,从上表可以看出,重要性的直接效应指标简单相关系数平方R2对应的差值为0.4584±0.0391,而总效应指标标准回归系数平方β2对应的差值为0.2810±0.0127,均不能满足估计值之和应该等于总模型的r2这一基本准则。而优势分析的偏差量为0.0000±0.0000,相对权重和乘积尺度法(βr)对应的差值分别为0.0019±0.0030和0.0079±0.0077,这三个方法的差值均比R2和β2小,且极接近0,尤以优势分析为甚。此外,可见样本量较小时,相对权重和乘积尺度法的重要性估计值之和与模型R2总仍有差距,当样本量增大时,估计值之和与模型R2间差值缩小,但相对权重仍好于乘积尺度。而优势分析则不受样本量变化的影响。
由于各样本均来自同一总体,因此各模拟数据集虽然样本量不同,但自变量相对重要性估计值之间仍具有可比性。以各自变量估计方法对应的差值作图如下,以观察各方法随样本量增大而出现的变化趋势:

图1 不同样本量的模拟样本中自变量重要性估计值
从上图可以看出,r2的估计值明显偏大,β2的估计值明显偏小,而优势分析、相对权重以及乘积尺度三种方法的估计值相差无几。虽然各样本均来自同一总体相关阵,但可以看出,样本量较小时,各方法的重要性估计值变异较大,随着样本量增大估计值也逐渐趋于稳定。
2.同一总体中重复抽样对各方法重要性指标的影响
随机抽样是研究者为了研究目标人群总体参数的重要手段,众所周知,随机抽取的样本并不能完全等价于总体。从上节的结果可以看出,当样本量较小时,各重要性评价方法的估计结果并不稳定,因此,有必要观察和比较从同一总体中重复抽样时,各方法的稳定性。
本研究中,重复抽样的总体仍沿用上节中的四各自变量相关阵,并模拟一个样本量为10000的数据集作为抽样所用的总体,抽样过程调用SAS中的PROC SURVEYSELECT 过程,样本量大小100。研究所用的总体相关结构和各自变量相对重要性见表4。
本次研究共完成1000次抽样,使用以上五种方法对每一个抽样样本进行相对重要性评价,将样本的估计值与总体参数相比较,并使用变异系数来评价各方法估计值的稳定性。结果如下:

表4 总体相关结构与自变量相对重要性
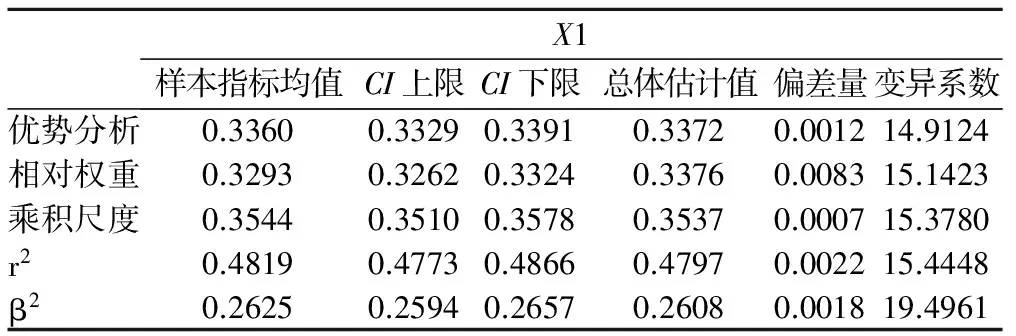
表5 抽样样本中X1的重要性指标估计值

表6 抽样样本中X2的重要性指标估计值

表7 抽样样本中X3的重要性指标估计值

表8 抽样样本中X4的重要性指标估计值
可以看出,优势分析、相对权重、乘积尺度(βr)和标准回归系数平方(β2)、简单相关系数平方(R2)在评价各自变量的相对重要性时,前三种方法的变异系数均比后两种方法小,表现出了更好的稳定性。从样本指标均值与总体估计值间的偏差量来看,相对权重法的偏差量为0.0009~0.0085,简单相关系数平方(R2)为0.0002~0.0080,变化较大。优势分析的偏差量为0.0012~0.0048,乘积尺度和标准回归系数平方的偏差量分别为0.0007~0.0028和0.0001~0.0032。
讨 论
评价不同样本量对重要性估计结果的影响时,研究结果显示标准回归系数平方的指标值之和明显小于模型中R2,而简单相关系数平方的指标值之和明显大于模型R2,其原因在前文中已有讨论,这也与其他研究者的结论一致。两方法的指标值之和与模型R2的差值也未随样本量增大而表现出明显的变化趋势。乘积尺度、优势分析、相对权重法三种方法的指标和与R2之差,均十分接近于0,其中优势分析法的差值为0.0000±0.0000,且不随样本量大小变化而改变。而相对权重和乘积尺度法(βr)对应的差值分别为-0.0019±0.0030和0.0005±0.0111。此外,可见样本量较小时,相对权重和乘积尺度法的重要性估计值之和与模型R2总仍有差距,当样本量增大时,估计值之和与模型R2间差值缩小。
为了评估对同一总体的重复抽样过程是否影响各方法的重要性估计结果,本研究使用了变异系数来作为评价指标,发现标准回归系数平方的结果变异程度最大,简单相关系数平方次之,而优势分析的结果变异最小,重要性估计结果最为稳定。
在实际工作中,需估计自变量相对重要性时,如果自变量间存在共线性,不应使用标准回归系数平方和简单相关系数平方等传统指标。相对权重法要好于乘积尺度法,但优势分析法对模拟R2的估计最为贴近。尽管优势分析法的计算较为复杂,但随着计算机硬件的升级,这一问题不再突出。因此当研究数据样本量较小时(<500)时,研究者应尽量使用优势分析法来进行自变量的相对重要性估计,样本量较大(>600)或为计算简便,可选用相对权重法。
[1]贾孝霞,伍立志,杨文.对策理论在线性回归模型自变量重要性估计中的分析及应用.第二军医大学学报,2014,25(8):865-869.
[2]代鲁燕,张波,黄启风.相对权重法在线性模型自变量相对重要性中的估计及其应用.中国卫生统计,2013,30(1):19-20.
[3]贾孝霞,伍立志,沈其君.线性回归中自变量重要性估计的平均秩序方差分解法.中国卫生统计,2014,31(3):535-537.
[4]Bring J.A geometric approach to compare variables in a regression model.Am Stat,1996,50(3):57-62.
[5]Budescu DV.Dominance analysis A new approach to the problem of relative importance of predictors in multiple regression.Psychol Bull,1993,114(3):542-551.
[6]Azen R,Budescu DV.The dominance analysis approach for comparing predictors in multiple regression.Psychol Methods,2003,8(2):129-148.
[7]Huo Y,Budescu DV.An Extension of Dominance Analysis to Canonical Correlation Analysis.Mult Behav Res,2009,44(5):688-709.
[8]Johnson JW.A Heuristic Method for Estimating the Relative Weight of Predictor Variables in Multiple Regression.Mult Behav Res,2000,35(1):1-19.
[9]Lebreton JM,Tonidandel S.Multivariate relative importance:Extending relative weight analysis to multivariate criterion spaces.J Appl Psychol,2008,93(2):329-345.
[10]张波,代鲁燕,黄启风.logistic回归中自变量相对重要性的相对权重估计.中国卫生统计,2012,29(2):191-192.
[11]Kaiser HF,Dickman K.Sample and population score matrices and sample correlation matrices from an arbitrary population correlation matrix.Psychometrika,1962,27(2):179-182.
[12]Fan X,Felsovaly A,Sivp SA.SAS for Monte Carlo Studies A Guide for Quantitative Researchers.SAS Publishing,2003.
[13]Cjap YCE,Zhao Y,Kupper LL.Quantifying the Relative Importance of Predictors in Multiple Linear Regression Analyses for Public Health Studies.J Occup Environ Hyg,2008,5(8):519-529.
(责任编辑:郭海强)
The Impact of Sample-size and Sample-process on Several Usual Importance Evaluate Methods
Wu Lizhi,Jia Xiaoxia,Shen Qijun
(SchoolofMedicine,NingboUniversity(315211),Ningbo)
Objective Implement random sample from a simulation population,to evaluate the The impact of sample-size and sample-process on several usual importance evaluate methods,observe the stability of those methods.Methods This study introduced existed importance methods,using PROC SURVEYSELECT procedure to sample a fixed population for 1000 times,generating 1000 same size sample,to evaluate the stability of relative importance methods.We sampled the population to generate datasets with different sample size to observe impact of sample-size on those methods.Results The sum of squared correlation coefficients′ estimator is bigger than model R-square,squared standardized regression coefficients′ sum is smaller.In contrary,sum of the Product Measure,Relative Weight and Dominance Analysis are extremely close to model R-square.When the sample size small than 1000,the estimator have obviously variation,but the variation decreased when the sample size rise up.Conclusion The dominance analysis has best stability,also has the best match of model R2in those methods.
Relative importance;Sample-size;Sample-process;Monte Carlo simulation
国家自然基金(81172771)浙江省医药卫生科技项目(2016KYB062)
1.浙江省疾病预防控制中心(310051)
2.浙江医药高等专科学校
3.宁波大学医学院预防医学系
△通信作者:

