改进的POCS算法的超分辨率单幅图像重建∗
朱耀麟,2王祖全齐静武桐
图像处理
改进的POCS算法的超分辨率单幅图像重建∗
朱耀麟1,2王祖全1齐静1武桐1
(1.西安工程大学电子信息学院西安710048)(2.西北工业大学电子信息学院西安710072)
超分辨率图像重建的目的是从几个低分辨率(LR)的模糊、有噪声、欠采样以及移位的图像中获得一个高分辨率(HR)高质量的图像。论文基于凸集投影的超分辨率图像重建算法,分析重建后图像边缘模糊的成因,提出了一种保留边缘的超分辨率变正则化图像重建的方法。该方法对退化图像建立精确的退化过程模型,通过自适应选取正则化参数动态调节重建误差逼近项和凸集约束项,从而实现超分辨率重建。在几张图片上的测试效果证明了论文算法相对于现有其他方法的优越性,该算法能够有效地保证复原求解的收敛性并保持复原图像的边缘细节,且峰值信噪比具有较大提升,对经模糊和噪声污染的图像有较好的复原效果。
图像重建;最大后验估计;凸集投影;正则化
Class NumberTN911.73
1 引言
超分辨率图像重建技术是在很多实际例子中对于提高图像分辨率是很实用的而且必要的,它可以弥补图像像素丢失,消除图像噪声,恢复图像细节信息,从而获得高分辨率图像。例如医学图像、卫星图像、视频软件等,它们的共同点是都能够获得几张内容相同的低分辨率图像。而相对于序列图像的超分辨率重建,单幅图像的超分辨率重建技术无需相同场景下的多幅低分辨率的图像,只需当前场景中的一幅低分辨率图像就可重构出同一场景下的高分辨率图像,在实际应用中能更加贴合需求。
单幅图像重建在1984年由Tsai等提出,利用同一场景下的多幅低分辨率图像序列间的互补和冗余信息重建出一幅高分辨率图像的序列图像重建算法。后来历经插值重建,序列重建和基于学习的重建三个重要阶段。HR图像的细节信息是通过LR图像的FFT或DWT变换的细节信息来估算的[1]。最成功的方法就是空间域上的随机方法,例如在文献[1~2]中利用多尺度空间域相似学习算法及曲率迭代插值算法,MAP(最大后验法算法),ML(极大似然算法)以及POCS(凸集投影法)。文献[3]利用基于Huber-Markov先验模型的MAP-POCS法实现图像的频谱外推,对频率分量进行校正,去除了调制传递函数过零点附近的伪信息。文献[5,7]利用学习的超分辨率方法对大量的高低分辨率图像样本进行训练最终获得图像的先验知识,再对图像进行超分辨率重建。文献[6,8]提出的基于例子的单幅图像超分辨率重建方法,通过马尔科夫网络学习得到高低分辨率图像之间的先验知识,这类方法的重建效果比较理想,尤其在人脸和文字处理领域,然而需要大量高低分辨率图像作为训练样本数据库。在所有这些方法中,可以引入一个价值函数[2],来做出HR和LR图像之间关系的线性模型,从而能够估算HR图像。然而,这些方法中用到的线性模型是一个难题,因为它的变换矩阵可能是单一的,因此唯一的解是不能获得预期效果的。
在本文中,通过选择保留边缘来稳定不适定问题的倒置,以及考虑噪声的影响,来解决重现HR图像的问题,已得的结果显示了这个新方法的性能。像重建的成像模型。
而参考帧的建立,一般采取对观察图像序列中的一帧进行双线性插值和迭代,使之达到所要求的高分辨率的办法。文献[4]中对混合MAP-POCS法初始值的构造往往采用双线性插值法,保证了观察图像中所有的点都被投射到参考帧中正确的位置[4]。修正参考帧的方法是基于PSF的,也就是把观察序列中的所有图像点投影到参考帧上,找出参考帧在它的PSF范围内的像素点,由PSF计算出这个像素点的灰度估计值,将其与观察序列中的实际值进行比较,如果误差超出了允许范围,就对参考帧中的像素点灰度值进行修正,使灰度估计值与实际值的误差减小到所要求的范围内[5,7]。
实际操作过程为:先选定参考帧,再计算各帧之间的运动矢量,并构造相应的算子Dk,然后将HR图像的任一初始估计值f0(通常是参考帧的双线性插值)投影到每一个约束集CK上,如下式所示:

式中n为低分辨率图像的数目。不断重复上述投影过程以更新高分辨率图像的估计值。SR重建问题的POCS方法在文献[6]被提出。设运动信息已知,然后可以根据每张低分辨率(LR)图像中的每个像素定义一个数据连续性约束集。任意(LR)图像的凸集可以由下式给出:
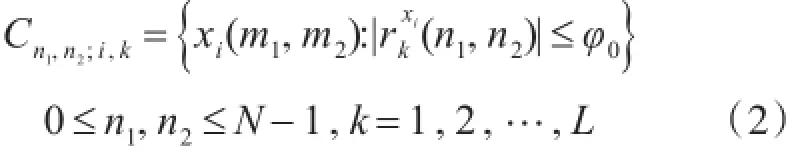
2 POCS算法原理
首先对超分辨率图像进行预估获得连续多帧低分辨率图像序列,也就是建立参考帧,然后根据观察图像序列对参考帧进行修正和插值放大作为参考图像,直至得到可以接受的复原结果[3]。
用矢量H表示原始高分辨率图像,L表示待重建的低分辨率图像,则成像模型表示为;L= DBMH+n,M是几何运动矩阵,B是模糊矩阵,D是下采样矩阵,n是附加噪声。此逆过程就是单幅图其中每个像素的值是被约束的,因此它是残差。

数量上在集合中被φ0所限制。由于φ0是由噪声的统计量决定的,理想图像的解是属于满足某个确定统计条件的集合的。
一个任意的xi(m1,m2)到Cn1,n2;i,k映射定义为

能量限制值,正定集,有限支持集等约束集都可以影响和改善结果。一个经常用到的幅度约束集为
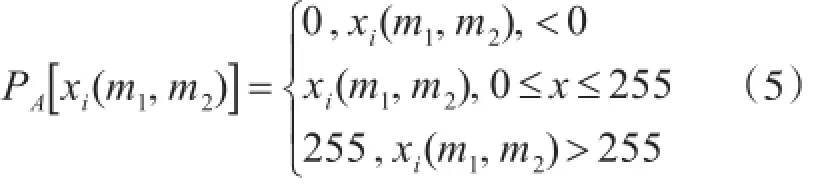
3 单幅图像重建的改进算法
从式(1)可以看出重建图像质量的好坏与双线性插值出来的初始估计有直接联系。而双线性插值是将原始图像上的各点首先对应到放大图像的各点,在此基础上作插值,并不区分边缘与平滑区域,这是造成边缘模糊的主要原因,因此改进算法要对边缘点进行正则化处理,用保持原始图像的边缘信息进行图像插补的方法代替双线性插值求解POCS算法中图像的初始估计[9~10]。算法重点处理的是沿边缘方向,沿边缘两侧,边缘到平滑区域的过度处理以及边缘密集区处理[11]。
4 改进算法仿真结果
在我们的仿真实验中,低分辨率图像由以下方法获得:由-10到10像素的平均分布获得随机移位,由5像素角度为5°的线性移位获得模糊效果,抽样值为L1=L2=2。此外,这些低分辨率图像还被高斯白噪声(AWGN)干扰,信噪比SNR=20dB。图1显示了莉娜的原始测试图片和它的低分辨率图片。为了从数值上评价该算法的效果,我们需要计算原始图像和重建图像的峰值信噪比PSNR和结构相似度SSIM[8]。以dB为单位的PSNR定义如下

其中N为像素总数,X为原始图像,X为重建图像[4]。

图1 (a)原始图像(两倍大小),(b,c,d,e)为四种用来估算高分辨率图像的LR图像序列
首先,为了挑选最佳的线性模型,尝试了许多权值(m)和偏移量(c)。表1显示了三个已知测试图像的结果。当m=10-10,c=0时得到最佳结果。
图2显示了三种算法对于莉娜图像的结果,以及对原始图像微分后的直方图,它显示出了三种方法中的误差量。
然后,评价了MAP,MAP-POCS和改进算法的效果,并通过不同的测试图片进行对比。表1显示了m=10-10,c=0时,不同图片使用ML、POCS-MAP算法、原始POCS算法和改进算法后的PSNR值。

表1 三种估值算法通过PSNR的定量效果比较

图2 a~d显示原始图像,而e~h显示了Barbara,辣椒,以及测试图像1,2经过改进算法重建后的图像
在视觉效果上,从图1~2可以看出本文方法较好地保留了原始图像的边缘及纹理等细节,其重建结果要由于原始POCS算法。而与文献[4]MAP-POCS法相比,单纯从图中很难根据人的肉眼区别出其差异。表1计算出了PSNR和SSIM数值,其中可以清晰地显示出其重建结果。MAP算法得到的复原图像图像内的噪声虽然减小了许多,但颜色度显得不纯正,边缘有震荡现象,噪声消除得不是很明显。MAP-POCS算法得到的复原图像,可以看到该图像轮廓的清晰度增强,边缘得到了较好的保持,边缘上的噪声带几乎看不到了,说明噪声减少了。而本文算法颜色较好,因为在超分辨率图像复原之前,我们对降质图像序列进行了去噪预处理,防止了噪声污染,减弱了图像边缘弱化和模糊。
5 结语
本文解决了从几个内容相同的低分辨率图像中获得一个高分辨率图像的问题,在对成像过程建立精确的边缘模型的基础上,采用变正则构造初始参考图像,在大量不同分辨率的各种图像上测试了我们的方法,并且与其他现有随机方法相比显示了其出众的效果,对模糊图像和噪声污染的图像有较好的复原效果。
[1]杨欣,唐庭阁,费树岷,等.基于投影修正和POCS的图像超分辨率重建[J].江苏大学学报:自然科学版,2013,34(5):564-568.
YANG Xin,TANG Tingge,FEI Shumin,et al.Image re⁃con-Struction with super-resolution based on projection modification and POCS[J].Jiangsu university:Natural Sci⁃ence Edition,2013,34(5):564-568.
[2]贾平,李家德,张叶.采用非局部均值的超分辨率重构[J].光学精密过程,2013,21(6):1576-1585.
JIA Ping,LI Jiade,ZHANG Ye.Using nonlocal average su⁃per-resolution reconstruction[J].Optical precision pro⁃cess,2013,21(6):1576-1585.
[3]刘梓,宋晓宁,於东军.基于多成分字典和稀疏表示的超分辨率重建算法[J].南京理工大学学报,2014,3(1):1-5.
LIU Zi,SONG Xiaoning,YU Dongjun.Composition based on dictionary and sparse representation of super-resolu⁃tion reconstruction algorithm[J].Journal of Nanjing Uni⁃versity of Technology,2014,3(1):1-5.
[4]王静,章世平,孙权森,等.基于MAP估计的遥感图像频域校正超分辨率算法[J].东南大学学报:自然科学版,2010,40(1):84-88.
WANG Jing,ZAHNG Shiping,SUN Quansen,et al.MAP based remote sensing image super-resolution with frequen⁃cy domain correction[J].Journal of Southeast University:Natural Science Edition,2010,40(1):84-88.
[5]H.Shen,P.Li,L.Zhang,Y.Zhao.“A MAP algorithm to super-resolution image reconstruction,”in Proc.IEEE Int.conf.Image and Graphics(ICIG'04),pp.544-547,2009.
[6]禹晶,苏开娜,肖创柏.一种改善超分辨率图像重建中边缘质量的方法[J].自动化学报,2007,33(6):577-582.
YU Jing,SU Na,XIAO Gen parker.a method to improve the edge of super-resolution image reconstruction quality[J].Journal of automation,2007,33(6):577-582.
[7]M.Elad,A.Feuer.Restoration of a single super resolution image from several blurred,noisy,and under-sampled measured images[J].IEEE Trans.Image Processing,2011,6:1646-1658.
[8]陈杰,朱秀昌.一种基于彩色化的单幅彩色图像超分辨率重建[J].南京邮电大学学报:自然科学版,2013,33(4):6-12.
CHEN Jie,ZHU Xiuchang.Based on the color of a single color image super-resolution reconstruction[J].Journal of nanjing university of posts and telecommunications:natu⁃ral science edition,2013,33(4):6-12.
[9]绍乐图,陈晨,张红刚,等.改进的混合MAP-POCS超分辨率图像复原算法研究[J].电光与控制,2015,2:41-45.
SHAO Letu,CHEN Chen,ZHANG Honggang,et al.Im⁃proved hybrid MAP-POCS super-resolution image restora⁃tion algorithm study[J].Electric and control,2015,2:41-45.
[10]江静,张雪松.图像超分辨率重建算法综述[J].红外技术,2012,34(1):24-30.
JIANG Jing,ZHANG Xuesong.Image super-resolution reconstruction algorithm review[J].Infrared technology,2012,34(1):24-30.
[11]史郡,王晓华.基于改进的K-SVD字典学习的超分辨率图像重建[J].电子学报,2013,41(5):9797-1000.
SHI Jun,WANG Xiaohua.Based on the improved KSVD dictionary learning super-resolution image recon⁃struction[J].Journal of electronics,2013,9(5):9797-1000.
An Improved POCS Algorithm for Super-resolution Single Image Reconstruction
ZHU Yaolin1,2WANG Zuquan1QI Jing1WU Tong1
(1.School of Electronics and Information,Xi'an Polytechnic University,Xi'an710048)(2.School of Electronics and Information,Northeasten Polytechnic University,Xi'an710072)
Super-resolution image reconstruction has been one of the most important research areas in recent years,whose goals is are to obtain a high resolution(HR)image from several low resolution(LR)blurred,noisy,under sampled and displaced images.Relation of the HR image and LR images can be modeled by a linear system using a transformation matrix and additive noise.However,an unique solution may not be available because of the singularity of transformation matrix.To overcome this ill-posed problem,stochastic methods such as ML and MAP have been introduced.However,their performance is not good because the effect of noise energy has been ignored.In this paper,an adaptive regularization approach is proposed based on the fact that the regularization parameter should be a linear function of noise variance.The performance of the proposed approach has been tested on several images and the obtained results demonstrate the superiority of our approach compared with existing methods.
image reconstruction,maximum a-posteriori,projection on convex sets,adaptive regularization
TN911.73
10.3969/j.issn.1672-9722.2017.05.035
2016年11月9日,
2016年12月25日
国家自然科学基金(编号:61303120);陕西省科技厅国际合作项目(编号:2016KW043);陕西省教育厅科学研究计划资助项目(编号:15KJ1320)资助。
朱耀麟,男,博士(后),副教授,硕士生导师,主要研究为图像处理和模式识别。王祖全,男,硕士研究生,研究方向:图像处理。齐静,女,副教授,研究方向:图像处理。武桐,女,讲师,研究方向:图像处理。

