多目标跟踪蜂拥控制算法研究与仿真∗

张金春1王帅磊曹彪3杨芸

多目标跟踪蜂拥控制算法研究与仿真∗

张金春1王帅磊2曹彪3杨芸2

（1.海军航空工程学院基础部烟台264001）（2.海军航空工程学院研究生管理大队烟台264001）（3.海军航空工程学院基础实验部烟台264001）

针对蜂拥控制算法在多目标跟踪问题中的应用，提出了多目标跟踪蜂拥控制算法。假设智能体不确定具有目标信息，通过Lyapunov稳定性理论，分析了使系统稳定的条件，给出了稳定状态的形式。并证明了如果智能体被预先指定了跟踪的目标，则每个群体达到蜂拥，并且不发生碰撞。对不同的网络初始连通性和两种目标运动模式分别作了仿真，证明了算法的有效性。

多目标；跟踪；蜂拥控制；Lyapunov稳定性；连通性；运动

Class NumberTP273

1 引言

蜂拥控制来源于对自然界生物群体的运动行为的观察和抽象，自提出［1～2］以来，引起了许多领域的研究人员的兴趣，并在多个方面做了大量研究，主要包括机器人［3～6］、移动传感器网络［7～8］以及控制算法［9～10］等方面。

在利用蜂拥控制算法进行多目标跟踪的研究中，钟午［10］针对传统算法中不利于系统收敛的局部作用力引入了排斥势能函数，并提出了新的多领导者蜂拥算法；罗小元［11］对跟踪不同目标的智能体分别建立了势场函数，实现对多目标的跟踪；Luo［12］给每个目标设置了可接受的智能体数量，并提出一种根据智能体与目标的距离来决定如何跟随多目标的算法，算法中包含了与距离相关的概率项；王海［13］提出以局部自适应追踪为基础的牵制算法，由少数信息个体带动邻居跟踪多个目标；ZHANG［14］在仅具有位置信息的情况下，将动态的复杂边界作为多个目标，利用智能体对其进行跟踪，实现对动态边界的实时监视。

已有研究中，对于智能体网络的连通性有不同的假设，并且智能体对于目标的信息获取方式有所区别，但缺乏系统的理论分析，关于目标的运动模式对智能体形成蜂拥的影响的研究也较少。本文在假设智能体预先不一定具有目标信息的基础上，提出了多目标跟踪蜂拥控制算法，给出了系统稳定的条件，并通过Lyapunov稳定性理论，系统地分析了算法的稳定性。针对不同的网络连通性和不同的目标运动模式，通过仿真验证了有效性。

2 蜂拥控制

2.1问题描述

在n维空间，考虑N个移动智能体的运动，将每个智能体视为质点。第i个智能体的位置为qi∈Rn，速度为pi∈Rn，其运动方程为

其中ui∈Rn为第i个智能体的控制输入项。

在任意时刻t，以智能体i所在位置为中心，感知半径r为邻域的半径，则邻域内所有其他智能体为i的邻居，记作

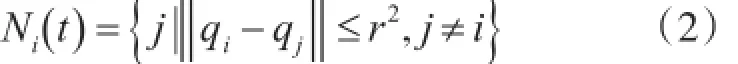
其中‖·‖为Euclid范数。

将智能体i视作网络的节点，智能体i与其邻居由无向边连接，系统内所有节点和连边构成的网络用无向图G(t)表示，对应的邻接矩阵为A(G(t))=[aij(t)]，其中

图G(t)的Laplacian矩阵为L(G(t))=[lij(t)]，其中

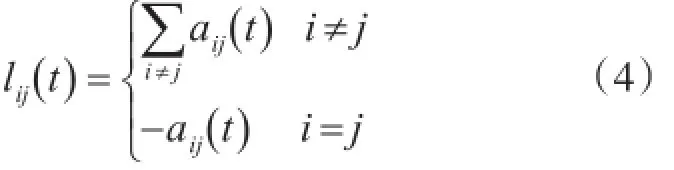
由定义可知，L(G(t))为半正定矩阵，简记为L。

假设系统中有M个目标，所有目标的运动方程都为：

其中q∈Rn和p∈Rn分别为目标的位置向量与速度向量。

2.2控制算法

按照Reynolds［1］提出的三条规则，智能体的运动要满足：1）分离：与邻域内其他智能体避免碰撞；2）聚合：与其他智能体保持紧凑；3）速度匹配：与其他智能体保持速度一致。根据Olfati-Saber提出的蜂拥控制算法［2］，智能体的控制输入为

其中，当智能体具有目标信息时，hi=1，否则hi=0，qγi为智能体i所要跟踪的目标的位置向量，pγi为目标的速度向量，uγi

为目标的加速度向量，下标γi表示该目标被智能体i跟踪。

本文中，如果智能体与目标的距离小于感知半径，则该智能体具有目标信息；如果智能体与目标的距离大于感知半径，但与目标之间有一条连通路径，则该智能体仍能通过其他智能体获得目标信息。因此在运动过程中，当‖‖qij≤r时，智能体i和j之间仅存在两种情况：1）hi=hj=0；2）hi=hj=1。因为‖‖qij≤r时，i和j之间存在通信，只要其中一个具有目标信息，不考虑通信延迟，则另一个也能够获取目标信息。因此，相邻的两个智能体只能同时具有或者同时不具有目标信息。推广到智能体组成的连通网络，如果其中至少存在一个直接型智能体，则整个网络中的所有智能体都能具有目标信息，即h1=h2=…=hN=1；否则h1=h2=…=hN=0，任意一个智能体不具有目标的信息，智能体只依靠相互之间的影响形成群集运动。

系统的总能量包括智能体之间的势能，智能体与目标之间的相对势能和相对动能，可以写作

因此，Q是一个正半定方程。在初始时刻t=0，假设系统能量Q(0)的值是有界的。

3算法分析

对于由智能体组成的系统以及多个目标，根据运动方程式（1）和式（5），控制输入式（7）和系统能量函数式（8），可以得出如下结论：

1）智能体与所要跟踪的目标的距离是有界的；

2）智能体的速度能够收敛到所要跟踪的目标的速度；

3）如果初始能量Q(0)＜(κ+1) e，其中e=minΨα()‖‖qij，则至多会有κ对智能体发生碰撞，当κ=0时，任何两个智能体之间不会发生碰撞；

证明：

在时间区间[tk-1,tk)内，对系统能量求导得

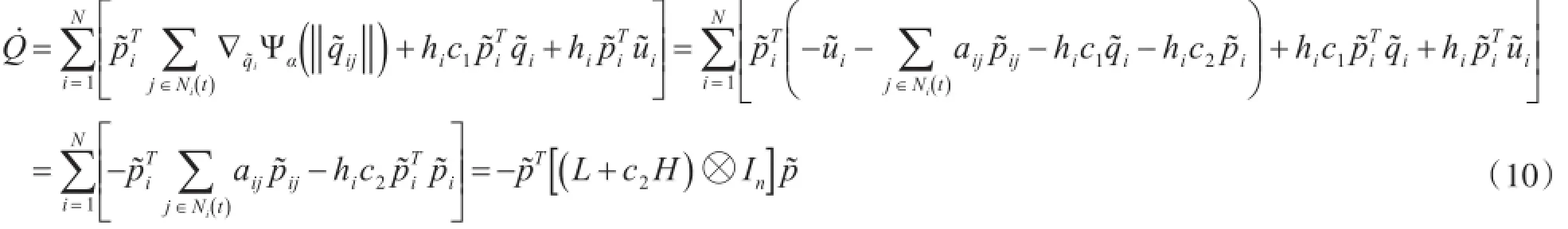
其中，H=diag(h1,h2,…,hN)。由于存在多个目标，对上式作如下处理。对任意时刻t，存在正交变换矩阵K∈RN×N，使矩阵L+c2H转换为分块矩阵，即其中Li为跟踪第i个目标的所有智能体组成的网络的Laplacian矩阵，Lm+1为不跟踪任何目标的智能体组成的网络的Laplacian矩阵，Hi为相应的由系数hi组成的对角矩阵。又令

则有

结合式（10），可以得到

对于系统能量Q有

其中d∈(0,r)。根据人工势函数的定义，新产生连边的能量值是有界的，因此Qmax也是有界的。对系统来说，仅存在有限个时刻，使得mt1+mt2+…+mtk≤M，即网络内的连边不会无限增加。

由式（9）和（11）可知，对hi=1有并有对hi=0，当且仅当=qi时满足集合：

是正不变紧集。根据拉萨尔不变性，所有始于Ω的解都会趋于最大不变集：当=0可知=0，即p=0，即对hi=1有 pi-pγi=0，对hi=0有pi=0。因此具有目标信息的智能体的速度会收敛到目标的速度，并且所有跟随相同目标的智能体的速度都会收敛到相同目标的速度；稳定状态时不具有目标信息的智能体保持静止。结论1和2证毕。

由式（17）可知，Q()t≤Qmax。如果有κ对智能体发生碰撞，则至少有κ+1个智能体发生了碰撞。根据人工势函数的定义，当两个智能体将要发生碰撞时，有因此有与假设矛盾，因此至多有κ对智能体之间能够发生碰撞。当κ=0时，任意两个智能体不会发生碰撞。

4仿真验证

通过证明可知，当h1=h2=…=hN=1时，所有的智能体都能够跟踪到目标。下面以此进行仿真验证。

4.1参数及条件

在二维平面上，考虑由50个智能体和3个目标组成的系统，指定10个智能体跟踪目标1，20个智能体跟踪目标2以及20个智能体跟踪目标3。初始状态下，智能体和目标的位置随机分布在[0,70]×[0,70]的区域内，智能体的速度随机分布在[-1,1]×[-1,1]的区间内随机选定，目标的速度在[-5,5]×[-5,5]的区间内随机选定。智能体的感知半径为r=6，智能体之间的期望距离为d= 5。σ范数中参数ε=0.1；定义ρh(z)中h=0.9；ϕ(z)中a=1，b=2；参数c1=0.1，c2=0.2。对智能体网络初始连通和非连通的情况都进行了仿真，并在两种情况下分别比较了目标作匀速运动和变速运动的情况。

4.2智能体网络初始连通

在初始时刻，智能体组成了连通的网络，3个目标的位置随机选定。图1中箭头的方向和长度表示速度的方向和大小。

目标在运动方程的作用下分别作匀速运动和变速运动时，智能体都能准确跟踪上相应的目标，形成一致的运动轨迹，最终分成了3个群体。按照预设的数量，10个智能体跟踪上了目标1，20个智能体跟踪上了目标2，20个智能体跟踪上了目标3，达到了预期目的。

图1智能体网络初始连通

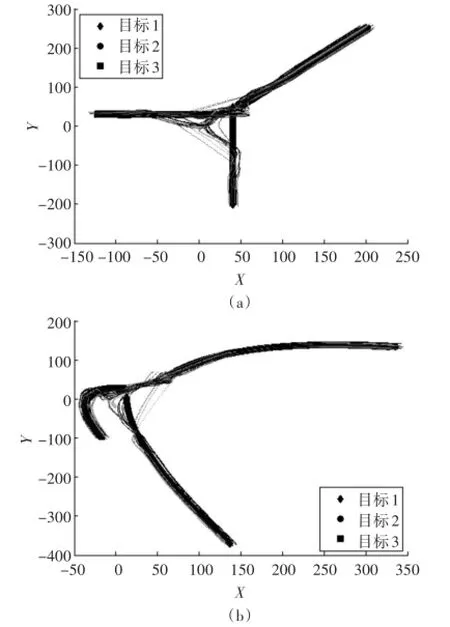
图2目标与智能体的运动轨迹

图3（a）和（b）为目标匀速运动时，智能体速度在X和Y方向上的收敛情况。图3（c）和（d）为智能体变速运动时，智能体速度在X和Y方向上的收敛情况。可以看出，经过一段时间的变化，每个智能体的速度都收敛到了相应目标的速度，并最终与目标速度保持一致。

4.3智能体网络初始非连通

在非连通条件下，智能体网络在初始状态的连通性较差，仅有少数智能体之间存在连接。

目标在运动方程的作用下分别作匀速运动和变速运动。尽管智能体网络在初始时刻的连通性较差，但智能体仍然能准确跟踪上相应的目标，形成一致的运动轨迹，并最终分成3个群体。按照预设的数量，10个智能体跟踪上了目标1，20个智能体跟踪上了目标2，20个智能体跟踪上了目标3，达到了预期目的。

图3 智能体速度收敛情况

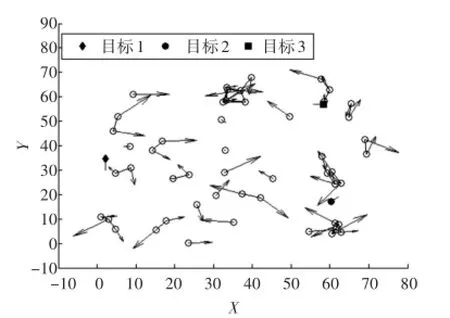
图4 智能体网络初始非连通

图5目标与智能体的运动轨迹

图6 （a）和（b）图为目标作匀速运动时，智能体速度在X和Y方向上的收敛情况。图6（c）和（d）图为目标作变速运动时，智能体速度在X和Y方向上的收敛情况。可以看出，智能体的速度仍然能够收敛到目标的速度，并最终与目标保持一致。

5 结语

本文提出了多目标跟踪蜂拥控制算法，理论上证明了该算法能够保证智能体准确跟踪上预设目标，跟踪相同目标的智能体速度能够达到一致，并形成稳定的群体运动。在网络初始连通和非连通条件下，分别比较了目标作匀速运动和变速运动的情况，仿真结果验证了算法的有效性。

图6 智能体速度收敛情况

［1］Reynolds C W.Flocks，Herds and Schools：A Distributed Behavioral Model［C］//ACM SIGGRAPH computer graph⁃ics.ACM，1987，21（4）：25-34.

［2］Olfati-Saber R.Flocking for Multi-Agent Dynamic Sys⁃tems：Algorithms and Theory［J］.Automatic Control IEEE Transactions on，2006，51（3）：401-420.

［3］Jia Y，Wang L.Experimental Implementation of Distribut⁃ed Flocking Algorithm for Multiple Robotic Fish［J］.Con⁃trol Engineering Practice，2014，30：1-11.

［4］Vásárhelyi G，Virágh C，Somorjai G，et al.Outdoor Flock⁃ing and Formation Flight with Autonomous Aerial Robots［C］//2014 IEEE/RSJ International Conference on Intelli⁃gent Robots and Systems.IEEE，2014：3866-3873.

［5］陈世明，聂森，谢竞，等.非完整移动机器人群体的优化蜂拥控制［J］.控制与决策，2012，27（12）：1839-1843.

CHEN Shiming，NIE Sen，XIE Jing，et al.Optimal Flock⁃ing Control of Nonholonomic Mobile Robot Swarm［J］. Control and Decision，2012，27（12）：1839-1843.

［6］王祥科，李迅，郑志强.多智能体系统编队控制相关问题研究综述［J］.控制与决策，2013，28（11）：1601-1613.

WANG Xiangke，LI Xun，ZHENG Zhiqiang.Survey of De⁃velopments on Multi-agent Formation Control Related Problems［J］.Control and Decision，2013，28（11）：1601-1613.

［7］La H M，Sheng W.Adaptive flocking control for dynamic target tracking in mobile sensor networks［C］//2009 IEEE/ RSJ International Conference on Intelligent Robots and Systems.IEEE，2009：4843-4848.

［8］娄柯，崔宝同，李纹.基于蜂拥控制的移动传感器网络目标跟踪算法［J］.控制与决策，2013，28（11）：1637-1642，1649.

LOU Ke，CUI Baotong，LI Wen.Target Tracking Algo⁃rithm of Mobile Sensor Networks Based on Flocking Con⁃trol［J］.Control and Decision，2013，28（11）：1637-1642，1649.

［9］Gazi V，Passino K M.A class of attractions/repulsion func⁃tions for stable swarm aggregations［J］.International Jour⁃nal of Control，2004，77（18）：1567-1579.

［10］钟午，张伟，康怀褀，等.一种改进的多领导者蜂拥算法及其性能分析［J］.小型微型计算机系统，2014，35（9）：2116-2121.

ZHONG Wu，ZHANG Wei，KANG Huaiqi，et al.An Im⁃proved Flocking Algorithm with Multiple Leaders and Its Performance Analysis［J］.Journal of Chinese Computer Systems，2014，35（9）：2116-2121.

［11］罗小元，李绍宝，关新平.多智能体多目标跟踪算法研究［J］.控制工程，2008，15（4）：420-422.

LUO Xiaoyuan，LI Shaobao，GUAN Xinping.Multi-tar⁃get Tracking Algorithm for Multi-agent［J］.Control Engi⁃neering of China，2008，15（4）：420-422.

［12］Luo X，Li S，Guan X.Flocking algorithm with multi-tar⁃get tracking for multi-agent systems［J］.Pattern Recogni⁃tion Letters，2010，31（9）：800-805.

［13］王海，罗琦，徐腾飞.融合局部自适应追踪的多目标牵制蜂拥算法［J］.计算机应用，2014，34（12）：3428-3432.

WANG Hai，LUO Qi，XU Tengfei.Multi-target Pinning FlockingAlgorithmCombinedwithLocalAdaptive Tracking［J］.Journal of Computer Applications，2014，34（12）：3428-3432.

［14］Zhang G，Fricke G K，Garg D P.Spill detection and pe⁃rimeter surveillance via distributed swarming agents［J］. IEEE/ASME Transactions on Mechatronics，2013，18（1）：121-129.

Research and Simulation on Multi-target Tracking Flocking Control Algorithm

ZHANG Jinchun1WANG Shuailei2CAO Biao3YANG Yun2
（1.Company of Basic Sciences，Naval Aeronautical and Astronautical University，Yantai264001）（2.Gradugate Administrative Group，Naval Aeronautical and Astronautical University，Yantai264001）（3.Basic Experiment Department，Naval Aeronautical and Astronautical University，Yantai264001）

For implementation of flocking control algorithm in multi-target tracking，this paper proposes a multi-target track⁃ing flocking control algorithm.It is assumed that each agent uncertainly have the information of a target.By Lyapuvov stability theo⁃ry，the paper analyzes the condition to make the system stable，and gives the stable state.It also demonstrates that if an agent has a presupposed target，then each group can form a flock，and no agents collide.The simulation verifies the effectiveness of it by differ⁃ent initial connectivity of the network and two kinds of movement patterns of the targets.

multi-target，tracking，flocking control，Lyapunov stability，connectivity，movement

TP273

10.3969/j.issn.1672-9722.2017.05.015

2016年11月17日，

2016年12月21日

张金春，男，硕士，教授，研究方向：复杂系统。王帅磊，男，硕士研究生，研究方向：军事系统的优化与控制。曹彪，男，硕士，讲师，研究方向：航空装备保障。杨芸，男，硕士研究生，研究方向：离散动态系统。