基于ARMA-GARCH模型的上证综指收益率波动性研究

文/刘旺强，上海大学

基于ARMA-GARCH模型的上证综指收益率波动性研究

文/刘旺强，上海大学

本文摘要：收益率波动性研究是资产定价领域研究的一个重要组成部分，本文以上证综指为研究对象，运用GARCH模型对2005年1月4日至2016年3月31日上证综指日收益率进行了实证研究。研究结果显示：上证综指收益率序列具有明显的波动集聚性和异方差的特征，即具有ARCH效应。基于时间序列特性的ARMA-GARCH模型能够较好的解释时间序列本身的自相关性以及条件异方差性，运用该模型可以较好地对上证综指波动情况进行拟合。

ARMA-GARCH模型；股票价格指数；波动率；ARCH效应

1 引言

上证综指覆盖了上海交易所所有上市公司股票，代表了大中小盘股股票的综合表现，行业分布均衡，指数的整体波动性较小，可以全面反映股票市场总体走势以及价格波动情况，具有良好的市场代表性。国内许多学者对上证综指进行了广泛的研究与论证。本文基于ARMA-GARCH模型对上证指数收益率序列的波动特性的基本特征进行分析，进而对近十年间上证指数收益率序列的变动情况进行模型拟合，以期对其波动情况进行预测。

2 模型介绍

2.1 自回归条件异方差模型（ARCH模型）

一般的回归分析和时间序列分析中，通常假设计量模型的随机扰动项满足同方差性。而一些时间序列特别是金融时间序列，经常会表现出波动性集群现象，其方差是随着时间变化而变化的，即表现出“异方差性”。Engle（1982）提出的自回归条件异方差模型（autoregressive conditional heteroscedasticity model，简称ARCH）模型很好的解决了时间序列的波动性问题，不断被用来研究金融市场的收益序列变化的问题，同时奠定了金融时间序列波动异方差模型的基础。

ARCH（p）一般形式如下：

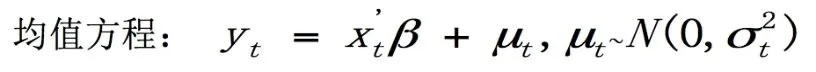
方差方程：

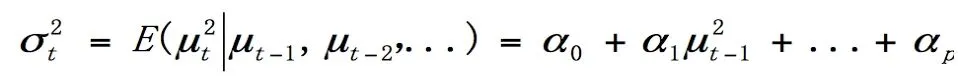
其中，yt和xt分别表示因变量和自变量， 表示不存在序列相关性的随机干扰项，p表示滞后阶数。模型还要求 ＞0， + +… ＜1。需要注意的是，ARCH（p）模型中仍然假设随机干扰项不存在序列相关，但是条件方差很可能存在序列相关，因此建模后还需要对残差序列是否存在ARCH效应进行检验。对残差序列进行ARCH检验的常用方法主要有残差平方自相关图检验法和拉格朗日乘数法。

ARCH模型最主要的特征是可以体现时间序列波动的时变性和波动集群性。

2.2 广义自回归条件异方差模型（GARCH模型）

GARCH模型成为广义自回归条件异方差模型，是ARCH模型的扩展，由Bollerslev（1986）提出，其一般形式如下：

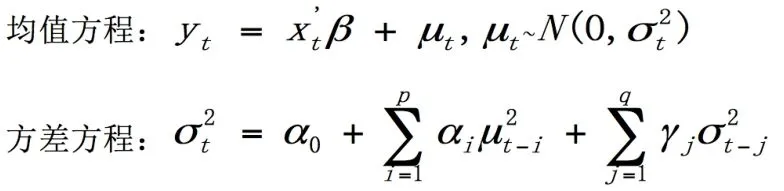
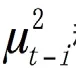
此外，ARCH族模型还包括GARCH-M（GARCH-in-mean）模型、TARCH（Threshold ARCH）模型、EGARCH（Exponential GARCH）模型等等。

3 实证分析

3.1 数据的选取与描述性统计分析

3.1.1 数据选取

本文选取2005年1月4日至2016年3月31日上证综指每日收盘价，共2730个数据。以相邻两天收盘价指数的对数一阶差分来代表上证指数的日收益率，计算公式为：Rt=ln（Pt）-ln（Pt-1），其中Pt和Pt-1分别代表t日和t-1日的收盘股价指数。

本文数据来源于Wind数据库，数据的处理采用EXCEL 2013、EVlEWS 8.0分析软件。

3.1.2 描述性统计分析

分别对2005年1月4日至2016年3月31日的上证综指收益率序列利用Eviews软件进行描述性统计分析，结果如下：

表1 上证综指日收益率序列统计特征

从上述描述性统计数据可看出，2005年1月4日至206年3月31日上证综指日收益率序列集中分布于0附近，均值较低，说明上证综指整体收益率较低。偏度为-0.545793，整体呈左偏。峰度为6.642316，说明日收益率序列分布较为集中，J-B统计量较大，为1643.999，且相伴概率接近于0，收益率不服从正态分布。

综上，结合上证综指收益率序列时序图（略）可见，上证综指日收益率序列具有时间序列普遍表现出的波动集群性和尖峰厚尾特性，且不服从正态分布。

3.1.3 上证综指收益率序列平稳性检验

序列的平稳性是时间序列分析的重要前提，为此需要对上证综指收益率序列是否平稳进行检验，下面采取单位根检验方法进行平稳性检验，结果如下表：

表2 上证综指日收益率序列平稳性检验

从上表可看出，上证综指收益率序列是平稳的时间序列。

3.1.4 上证综指日收益率序列ARCH效应检验

从收益率序列时序图（略）可直观看出，收益率序列出现大的波动后往往伴随着大的波动，小的波动后面伴随着更小的波动，即波动具有集群性，这说明收益率序列的误差项具有异方差特征，为此对收益率序列的残差序列进行ARCH效应检验，检验方法通常采取ARCH LM检验法以及残差自相关图（Q检验）法。此处以ARCH LM检验方法对上证综指收益率残差序列进行ARCH效应检验，结果如下表所示：

表3 上证综指日收益率序列ARCH效应检验结果

从表3可看出，P值接近于0，小于置信度0.05，拒绝原假设，即残差序列存在ARCH效应。

通过残差平方的自相关图也可看出，上证综指收益率序列的残差平方自相关系数（ACF）与偏自相关系数（PACF）不显著为0，也验证了收益率残差项存在ARCH效应。

3.2 ARMA-GARCH模型建模

考虑到上证综指收益率序列具有的异方差特性以及自相关性，本文拟考虑建立ARMA-GARCH模型对2005年1月4日至2016年3月31日上证总指数收益率序列进行模型拟合。结合上证综指收益率序列残差自相关图与偏自相关图，考虑其截尾与拖尾情形，并根据AlC信息准则，最后确定以ARMA（1,1）模型为上证指数收益率序列的均值方程。就波动率方程而言，一般的GARCH（1,1）模型能够较好的模拟大多数时间序列波动情形以及较好地解释时间序列的异方差性。因此，最后确定以GARCH（1,1）模型来模拟收益率序列的波动。

综上而言，最后确定以ARMA（1,1）-GARCH（1,1）模型来模拟上证综指收益率序列，最后得到的方程如下所示：

从分析结果可以看到，所有的参数都是显著的，说明前面验证的上证综指收益率序列存在的自相关性与异方差特性确实存在，括号中的z统计量以及AlC与SC值也说明ARMA（1,1）-GARCH（1,1）模型对上证综指收益率序列的拟合度较高，能够很好的解释收益率序列的波动特性。

4 结论与政策建议

从上述实证研究结果可以看出，上证综指收益率序列所具有的波动集群性表明我国股票市场波动幅度较大，我国股票市场发展还不太完善，历史发展环境的制约，我国股票市场特有的模式以及运行机制上的特殊性决定了我国股票市场价格波动还存在诸多风险。

针对上述问题并结合本文研究结果，在此提出一些建议：

（一）完善市场监管，尽量减少政府对市场的直接干预，适时适度引导。政府对于股市的频繁干预是我国股票市场的一个重要问题，应适时适度发挥政府作用，加强监管。

（二）建立股票市场信息发布及传递机制，确保股市信息能够准确快速及时地传递，最大程度减少信息不对称带来的弊端，防止股票市场的大度波动。

（三）我国股票市场发展尚不成熟, 波动具有条件异方差效应,政府可以利用其计量工具进行模拟和预测分析结果, 制定相应政策, 提高股市监管能力, 而投资者则可以运用股市波动规律, 从而尽可能规避市场风险。

[1]高铁梅.计量经济学分析与建模-EVIEWS应用与案例[M].清华大学出版社.2006

[2]刁艳华，李文华：基于Garch 模型的股票市场股指收益率波动性研究[J].财税金融，2013，06（02）：76-77

[3]黄慧：中国股市波动特征的实证研究——基于GARCH 族模型[J].科技创业，2015,8（23）:48-49