一种改进的交叉组合包分类研究

本文提出一种改进的基于交叉组合的包分类方法，基于对各维空间的无重叠的划分基础上进行分类，采用等价区间的办法来降低空间需求，该方法在提高处理速度的同时，所需存储空间也降低了三分之二。使用自治系统网络前缀产生模拟的分类数据库，用非随机方式及随机方式产生不同大小的数据库来对这个算法进行了验证，证明了这个算法的有效性。

【关键词】包分类 交叉组合 等价区间

数据包分类指根据数据包所携带的IP包头、传输层头部信息等查找预先设置的分类器，根据匹配规则来区分不同的数据包。包分类的结果决定了数据包应得到什么样的服务等级或者数据包属于哪一个数据流，包转发引擎根据分类的结果采用相应的处理。在千兆网络取证系统中，网络取证机数据包的采集、分析及转发是整个系统的核心，由于被取证机的网络数据量异常庞大，这就要求网络取证机对IP包进行分类，根据分类结果完成对数据包的不同过滤处理，对感兴趣的IP数据包进行转发存储至取证存储机，其它数据流进行丢弃，再转发至后端的取证分析机。

包分类的数据模型如下：一个数据包分类器包含M条规则RLj（1≤j≤M），如果对报文头的S个字段进行分类，规则RLj包含以下几个部分：

（1） RLj[i]（1≤i≤K）：用于表示数据包头的K个字段关系的正则表达式，它可以是特定的值、前缀表达式或是作用范围等；

（2）优先级Pri（RLj）：它定义了在分类器中规则的优先级，用来决定当数据包匹配多条规则，哪条规则有更高的优先级。

（3）Act（Rj）：它表示当规则匹配时，应该执行的动作。

假定数据包P的包头有K个字段（F1，F2，…，Fk），K维的包分类器可以在所有匹配规则中寻找到优先级最高的规则RLh，即：Pri（RLm）>Pri（RLi），1≤i≤M且i≠h。RLh被认为是数据包P的最佳匹配规则。

在包分类问题，主要在以下方向进行研究：基于并行分解-综合的算法。先将多维查找分解成并行的几个查找，然后综合它们的结果，最后得到匹配结果。例如BV，ABV等算法就是通过并行来查找各维的匹配情况，然后将各维的匹配结果通过规则映射的位图“位与”得到匹配规则，这类算法的缺点是当规则库比较大时，得到的位图会比较庞大。RFC算法借助于硬件流水线的方法，通过多阶段的并行分解过程，可以达到很好的查找性能，但缺点是性能通常受到阶段数和如何选取前一阶段结果的策略等因素的制约。而交叉组合（Cross-Product）算法通过并行查找各维匹配的前缀，从它们的各种组合中选出合适的匹配规则，交叉组合法在查找的时间上有很大的优势。在K维的情况下，它只需要K次线性查找和一次查表的时间，时间复杂度为O（KN）。但它的空间复杂度却是O（NK），在实际应用中可能因交叉组合表太大，造成路由器的存储体无法存储的情况，能不能在提高查找的速度的同时，对空间进行压缩呢？以下提出了一种改进的交叉组合算法。

1 改进的交叉组合算法

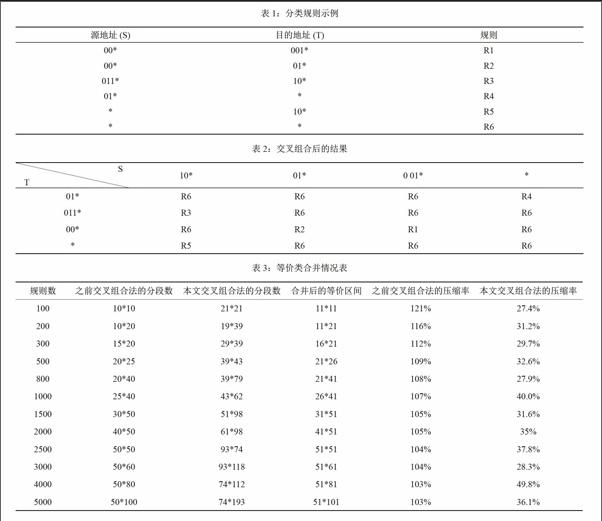
对于D维的情况，交叉组合需要进行D次的线性查找。由于地址范围相互之间可能重叠的原因，只能顺序查找方法，而不能采用快速的一维查找方法；每一维同一个IP包地址可能与几个部分同时匹配，所以可能匹配多条规则，需要从多条规则中寻找出最高优先级的规则。因此这一查找的效率并不是很高。表1是一个分类规则集的示例，对规则集C中地址S，T进行排序，产生交叉组合表如表2所示。

当使用交叉组合法来查找点P（0110，1000）时，则需要先对S进行顺序查找，得到匹配的S为{01*，011*，*}，再对T进行顺序查找，得到匹配的T为{10*，*}，再查表2，可得到6条匹配规则{R3，R4，R5，R6}，找出其中优先级最高的规则R3（假设以序号前后做为优先级的高低），以R3为最佳匹配规则。

以上过程可以看出，由于在每一维（S，T）中，规则所定义的范围相互之间有冲突，会有重叠区域，这样在各维的查找结果会存在多个匹配的前缀。

图1给出规则库的交叉组合区域图，R3、R4、R5和R6有共同的相交区域。当寻找H点的匹配规则时，有4条规则都匹配，由于R6与其它区域都相交，故任一次匹配查找都会找到R6，当某个点与其它规则（R1-R5）相匹配，必然与R6相匹配。

为了去掉这种区域的重叠，可以尝试换一种分段方法，将图1按图2进行分段，在X轴方向划分4个区间：X1、X2、X3、X4；在Y轴划分5个區间：Y1、Y2、Y3、Y4、Y5。这样就得到了20个划分区域，并且这些区域互不相交。每个区域内的点要么全部与规则R相匹配，要么全部与规则R不匹配。如果出现匹配多条规则的情况，由于区域内的各个点具有相同的性质，它们具有相同的最佳匹配规则。因此可以在建立查找表时先计算每个区域的最佳匹配规则，存储时就只存储最佳匹配规则即可。

2 实验分析

我们模拟一些规则数据库对本文的算法进行测试。交叉组合算法在最坏情况下，它的查找时间为O（KlogN），一般认为这种查找时间是很快的了。但它的空间复杂度达到了O（N2），因此，我们主要在存储空间的占用方面加以模拟。我们假设有两个自治系统AS-A和AS-B，它们之间的边界路由器直接相连的，每个自治系统都有一定数量的前缀地址。我们模拟在自治系统的边界路由器中对数据包的分类，我们将一个自治系统的前缀地址与另一个自治系统的前缀地址交叉组合，并在路由器中定义从一个自治系统到另一个自治系统的包的规则。例如，假设自治系统1有30个前缀，自治系统2有20个前缀，交叉组合就可得到了一个600条规则的数据库。

我们所有的规则数量虽然很多，但是各规则的动作种类并不多，在实验中我们假设每个规则库的动作种类只有其中规则数量的3%。例如对于一个有1000条规则的数据库来说，只有30个不同的动作，等价类合并实验结果如表3所示。

由表3可以看出：

（1）基于本文所提出的交叉组合法，在每一维的分段比以前的方法的分段增加了许多。这是因为这个算法在最坏情况下的分段数为（2N+1）*（2N+1），而原方法在最坏情况下分段数为N*N。

（2）利用合并等价类的方法，有效地压缩了交叉组合表的大小，压缩率达到了1/3。

（3）对于前缀形式的目的地址和源地址，按等价类的方法合并后，每一维的分段合并后不超过N+1个等价类。

总之，对于规则数据库，经过合并等价类后，交叉组合表已经很小了，其中的冗余度已经不大了，例如对于有5000条规则的数据库，用原方法其交叉组合表只有5000项，用本文的方法也只有5151项，所以在这种情况下，是基本不用压缩的。本文提出的方法的意义在于提高了搜索的速度。

3 结语

针对交叉组合法速度快，但对存储空间的需求大的问题，本文提出了对交叉组合法进行改进的方法。第一是采用無重叠区域的交叉组合法。将每一维地址分为若干类，然后交叉组合，由这种分类方法分出的各个类，无论是在一维还是二维上，它都是有重叠的，无法采用快速的查找方法。本文采用的基于各维对空间的无重叠的划分的基础上的分类，从而在每一维的查找上可以使用较快的算法，提高了搜索的速度，降低了时间复杂度，由O（KN）下降到了O（KlogN），但也加大了空间需求。第二个方面采用等价区间的办法来降低空间需求。对于具有N条规则的规则数据库来说，本文证明了：通过等价区间合并方法，每一维的分类数不大于N+1个，其空间复杂度在O（N2）。该方法在提高处理速度的同时，还成倍地降低了对存储空间的要求。

参考文献

[1]刘震宇，李卫军，赖粤.基于网络处理器的并行包分类方法[J].计算机应用.2010，30（02）：306-315.

[2]曹婕，陈兵.一种内存优化的RFC包分类算法Merge_RFC[J].小型微型计算机系统，2012，33（04）：865-868.

[3]亓亚烜，李军.高性能网包分类理论与算法综述[J].计算机学报，2013，36（02）：408-421.

作者简介

李戈（1979-），女，河南省内乡县人。硕士研究生。讲师。主要研究领域为网络信息安全，智能信息处理。

作者单位

河南水利与环境职业学院机电与信息工程系 河南省郑州市 450000