基于模糊C均值聚类算法的区域用电特征分析

雷景生, 余修成

(上海电力学院 计算机科学与技术学院, 上海 200090)

基于模糊C均值聚类算法的区域用电特征分析

雷景生, 余修成

(上海电力学院 计算机科学与技术学院, 上海 200090)

某区域内电力用户的用电行为往往会影响该区域电力公司的负荷调度以及分时电价等重要问题的决策.为使得这些决策更符合该区域的实际情况,必须对该区域的用电特征进行分析.针对这一问题,提出了一种基于聚类算法的区域用电特征分析方法.采用模糊C均值算法并结合K-means算法,按照某区域的电力用户分布情况,将数据样本聚类为居民区电力用户、商业区电力用户和工业区电力用户3个类簇,并结合该地区实际用电情况,对得到的类簇负荷曲线进行了分析,得出了该区域不同类型电力用户的用电特征.

模糊C均值聚类; K-means算法; 负荷曲线;用电行为; 特征分析

在发展智能电网的今天,诸如智能电表等智能设备已在电力领域得到广泛应用,它不仅能够使人们在决策支持系统上实现电网可靠、安全、经济、高效的运行,也使供电侧和需求侧不断得到协调优化[1].然而对于影响电力公司电价分时调节[2]、负荷调度[3]等更细节一点的因素,则必须考虑不同区域不同类型的电力用户的用电行为,以及影响这些用电行为的时间、季节、用户分布等因素.在众多智能设备的支撑下,如何更加细致地分析需求侧电力用户的用电特征将是需求侧管理的重点研究领域之一[4].

目前,对于区域用电特征的分析主要集中在区域负荷特性方面,常采用聚类的方法,例如K-means聚类[5]、模糊C均值(Fuzzy C-means,FCM)聚类[6-7]、层次聚类、高斯混合模型聚类(Gaussian Mixture Model,GMM)、自组织特征映射(Self-organizing feature Map,SOM)神经网络、支持向量机(Support Vector Machine,SVM),以及一些集成的综合算法等.上述算法都有其各自的优点和不足,并且不同的算法对不同的样本数据有着特定的适用范围.根据数据样本的特点选取合适的算法,并在此算法的计算结果上通过多角度分析,进而依据不同类型用户的负荷变化情况进行研究,可以更好地刻画用户的用电行为[8].

针对这一问题,本文首先采用FCM聚类的方法对所采集的居民区、商业区、工业区等不同电力用户的负荷数据进行聚类,结合该区域用户分布的特点并尝试选取聚类数C的值、综合聚类后负荷曲线的特点,最终将该区域的负荷数据确定为3大聚类[9-10].同时,为了防止过分依赖单一聚类方法导致误差过大的情况,本文同时采用K-means聚类算法并与FCM聚类算法的聚类结果进行对比,然后结合两种算法的聚类结果分析该区域3种类型电力用户的用电特征[11-12].基于聚类结果,本文从不同角度进一步分析了3种不同类型电力用户各自的特点及其差异,进而总结出该区域电力用户的用电行为特征.

1 FCM聚类算法

聚类属于无监督学习的范畴,与有类别的回归、朴素贝叶斯、支持向量机等有类标签算法不同,FCM聚类算法是在预先没有给出类标签的情况下,基于目标函数,通过迭代的方式将隶属度最大的样本归为某一类.

与K-means聚类算法相比,FCM聚类算法引入了隶属度矩阵U(即模糊划分矩阵)和模糊系数m,从而将K-means算法中的硬隶属度关系提升为软隶属度关系,改变了K-means算法中某一对象非此即彼的隶属性特征.隶属度矩阵U中所有元素表征对应的对象隶属于相应类簇的隶属程度,而如果某一对象与某一簇的隶属度最大,就将该对象归属为该类簇.

1.1 FCM算法构成

设数据集data中含有n个向量xi(i=1,2,3,…,n),欲将n个向量聚类为C类,将μij定义为向量xj隶属于第Ci类的隶属程度即为隶属度,μij取0到1之间的小数.由于每个向量xi对于每一类都有一个隶属度参数,因此就要求对于某一个特定的向量隶属于每个类的隶属度的总和等于1,即:

(1)

FCM聚类算法的目标函数定义为:

(2)

(3)

(4)

式中:U——隶属度矩阵; V——聚类中心向量矩阵; μij——隶属度; m——模糊系数,根据经验通常取m=2; dij2——在欧式距离下元素对象xj到中心点Ci的距离.

因此,该目标函数表示数据集data中所有点到各个类中心的加权距离之和.

当目标函数取最小值时,通常认为取得最优聚类结果.最优聚类目标函数的表达式为:

(5)

(6)

式(6)两边同时对μij求偏导,得到:

(7)

(8)

式(6)两边对ci求偏导,可得:

(9)

1.2 FCM算法的具体实现步骤

(1) 初始化,以确定聚类数C,模糊系数m(m>1,通常取2),最大迭代次数T,收敛精度ε的取值;

(2) 随机生成隶属度矩阵U,并对其进行初始化使其满足式(1);

(3) 利用式(9)计算聚类中心ci;

(4) 计算目标函数式(2),如果式(2)的结果小于收敛精度ε或者达到最大迭代次数,则算法停止;

(5) 计算隶属度矩阵U;

(6) 重复步骤3,步骤4,步骤5,直到算法终止.

2 区域用电特征分析模型

2.1 数据的采集与预处理

对某一区域工作日内300个不同类型电力用户进行24 h的负荷取样,从00∶30时刻开始一直到次日00∶00时刻,每30 min记录一次负荷数据,共采集一天中48个时刻的负荷数据,部分负荷数据样本如表1所示.

为防止算法迭代的计算过程中因数据太大而产生的误差,本文对采集的数据进行预处理以消除不良影响,即将所有数据除以最小负荷值得到初始化后的负荷聚类数据样本.

表1 部分时刻的部分负荷数据样本 个

2.2 FCM聚类算法C的确定以及聚类结果

FCM算法聚类的前提条件是先确定C的取值,而通常情况下聚类数目都是人为确定的,因此本文依次尝试聚类数目C的取值并结合该区域实际的用户分布特点来确定C值.然后在MATLAB v8.4软件环境下读取采集的负荷数据,利用FCM聚类算法对初始化后的300个用户负荷数据进行聚类.选取聚类中心点矩阵作为聚类结果,通过可视化操作对其进行作图,以便在图中清晰地看出FCM算法的聚类结果.

2.3 FCM算法与K-means算法聚类结果对比

虽然FCM聚类算法在处理离群点数据以及对数据的利用上优于K-means算法,但是为了防止FCM聚类算法在应用于该数据对象时产生误差,本文采用经典的K-means聚类算法对相同的样本数据进行聚类.将两种算法的聚类结果进行比较,如果K-means算法也能够得到相似的聚类结果,那么结合两种算法的聚类结果就能更为准确地分析该数据样本中不同电力用户类型的用电特征.

2.4 不同类型电力用户用电特征分析

基于FCM聚类算法对所采集的数据进行聚类分析,既可以从时间角度横向分析所属居民区、商业区和工业区等几种不同类型电力用户的用电习惯,也可以从纵向角度分析这几种类型电力用户用电量的差异以及用电量的增长和变化情况.

3 数据分析实例

某区域工作日内居民区、商业区、工业区等各种类型的300个电力用户一天内48个时刻的负荷分布情况如图1所示.

尽管我们知道居民区电力用户的负荷小于商业区电力用户的负荷,商业区电力用户的负荷小于工业区电力用户的负荷,但在图1中无法明显地区分出这3类用户的负荷曲线.

采用FCM聚类算法对采集的300个用户数据进行处理,可得到如图2所示的聚类结果.

结合该区域采集数据时了解到的实际情况,得知该区域主要用户类型为工业用户、商业用户、居民用户以及少量的其他类型用户,所以C=2显然不符合实际的聚类结果,当C=4,C=5以及C选取更大的数时,各条曲线并没有典型的聚类特征且区分不明显,而当C=3时,聚类的结果具有明显清晰的聚类特征,也更符合该区域实际的用户分布情况.所以对于该区域所有类型的电力用户数据,本文将其聚类选为3个类簇,即工业区电力用户类型、商业区电力用户类型和居民区用户类型.

图1 300组电力用户的负荷分布

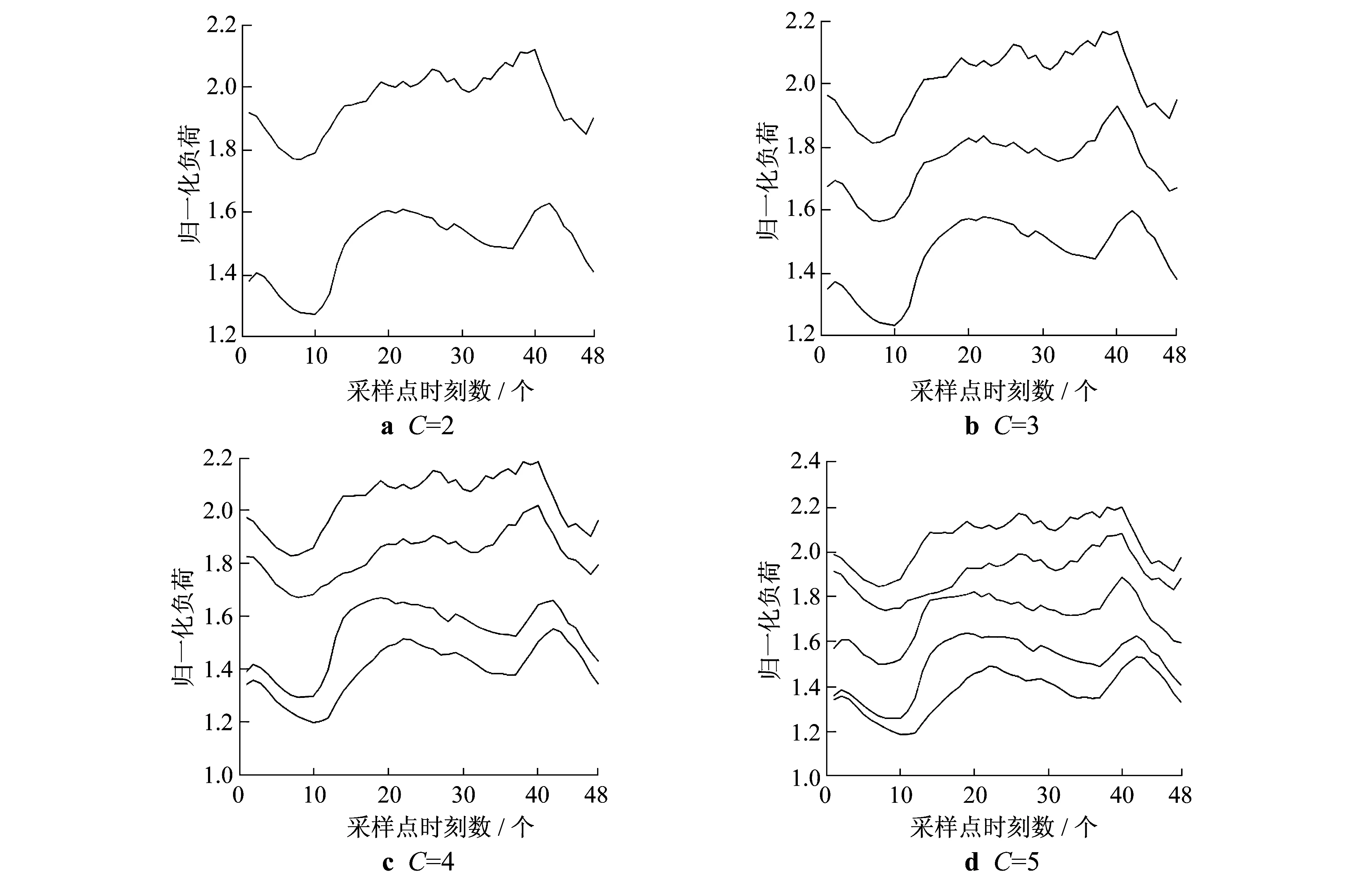
图2 FCM算法聚类结果

因此,图2b中C=3时即为该区域电力用户类型的聚类结果,图中3条曲线分别代表居民区电力用户类型、商业区电力用户类型和工业区电力用户类型,也反映了这3种类型用户的用电特征.

为了保证算法对于当前数据样本的准确性和有效性,采用经典的K-means聚类算法对相同的数据样本做聚类处理并比较聚类结果,若K-means聚类算法的结果与FCM聚类算法的结果相似,那么综合两种算法的聚类结果就能够准确有效地分析出各类型电力用户的用电特征.

图3为利用K-means聚类算法将相同的数据样本聚为3类得到的聚类结果.与图2b进行对比可以发现,图3中每一类中心点的负荷曲线与图2b对应的中心点负荷曲线基本一致.

图3 K-means算法聚类结果

结合该区域实际的用电量情况可知,3条曲线自上而下分别代表工业区电力用户类型、商业区电力用户类型、居民区电力用户类型.

综合两种算法的聚类结果,从横向的时间角度分析,这3种类型的电力用户几乎都是在凌晨4∶30左右达到负荷的最低值.这与人们的作息规律有关,活动的人口进入休息状态,机械、电器以及照明设备等用电器都处于关停状态,因此在4∶30这个时间点上3类用户的负荷都处于最低值.4∶30～7∶00这个时间段内,3类用户负荷都呈上升趋势,其中居民区的电力用户负荷增长的速度最快,商业区电力用户负荷增长速度相对最慢.7∶30～21∶00为3种电力用户的负荷高峰期,商业区用户负荷波动最大,居民区用户负荷波动相对最为平缓.在17∶00～21∶00这个时间段内,居民区用户负荷下降到负荷上升的过程相对于其他两种用户类型滞后约30 min,工业区电力用户与商业区电力用户几乎都是在20∶00达到负荷峰值,居民区电力用户在21∶00达到负荷峰值.21∶00至次日00∶00,3种类型电力用户负荷都处于明显下降趋势,工业区电力用户负荷下降有明显的波动,居民区电力用户负荷下降较为平缓.

从纵向的负荷角度分析,图2b和图3反映的3条负荷曲线整体负荷增长和下降情况大体相似,工业区电力用户的负荷大于商业区电力用户的负荷,且负荷约是它的1.2倍;商业区电力用户的负荷大于居民区电力用户的负荷,且负荷约是它的1.26倍.从负荷波动的趋势看,工业区电力用户整体负荷曲线波动最为明显,且波动集中在负荷高峰期的时间段内;商业区电力用户负荷曲线波动较小,也集中在负荷高峰期的时间段内;居民区电力用户整体负荷曲线比较平滑,波动很小.

4 结 语

采用FCM聚类算法对采集的数据样本进行了聚类处理,得到了某区域电力用户的聚类结果.为防止该算法对于特定数据样本产生的误差而影响分析结果,又结合了经典的K-means聚类算法,得到代表不同类型电力用户负荷分布的曲线.对于不同类型电力用户的聚类结果,分别从负荷曲线横向的时间方向上和纵向的负荷方向上得出了该区域不同类型电力用户的用电行为特征.通过实验分析表明,对用户用电行为特征进行分析,可以帮助电力公司对该区域的负荷调度和分时电价等情况作出更为准确有效的决策,对工程实践具有一定的指导意义.

[1] 王锡凡,肖云鹏,王秀丽.新形势下电力系统供需互动问题研究及分析[J].中国电机工程学报,2014,34(29):5 018-5 028.

[2] 徐永丰,吴洁晶,黄海涛,等.考虑负荷率的峰谷分时电价模型[J].电力系统保护与控制,2015,43(23):96-103.

[3] 李慧星,高赐威,梁甜甜.华东区域智能电网环境下的负荷调度[J].华东电力,2012,40(1):82-86.

[4] 黄宇腾,侯芳,周勤,等.一种面向需求侧管理的用户负荷形态组合分析方法[J].电力系统保护与控制,2013,41(13):20-25.

[5] 杨大勇,葛琪,董永超,等.基于K 均值聚类的光伏电站运行状态模式识别研究[J].电力系统保护与控制,2016,44(14):25-30.

[6] 孟安波,卢海明,李海亮,等.纵横交叉算法优化FCM 在电力客户分类中的应用[J].电力系统保护与控制,2015,43(20):150-154.

[7] ZHANG D Q,CHEN S C.A comment on alternative C-means clustering algorithms [J].Pattern Recognition,2004,37(2):173-174.

[8] 尹玉芬.地区电力系统负荷特性分析与需求侧管理研究[D].广州:华南理工大学,2010.

[9] 刘永光,孙超亮,牛贞贞,等.改进型模糊C均值聚类算法的电力负荷特性分类技术研究[J].电测与仪表,2014,51(18):5-9.

[10] 韩玉环,赵庆生,郭贺宏,等.基于FCM 的暂态电能质量扰动识别[J].电力系统保护与控制,2016,44(9):62-68.

[11] 孟建良,刘德超.一种基于Spark 和聚类分析的辨识电力系统不良数据新方法[J].电力系统保护与控制,2016,44(3):85-91.

[12] 普运伟,金炜东,朱明,等.核模糊C均值算法的聚类有效性研究[J].计算机科学,2007,34(2):207-229.

(编辑 胡小萍)

Fuzzy C-means Clustering-based Algorithm for the Analysis of Regional Electric Power Characteristics

LEI Jingsheng, YU Xiucheng

(SchoolofComputerScienceandTechnology,ShanghaiUniversityofElectricPower,Shanghai200090,China)

The behaviors of power users in some areas tend to affect the power load dispatching,time-sharing electricity price,and some other important problems on decision-making.It is necessary to analyze the regional electric-using characteristics to ensure that this decision is suitable for the local situation.To solve this problem,the analysis method of regional electric-using characteristics on clustering algorithm is put forward.The experiment adopts the fuzzy C-means algorithm and K-means algorithm,and according to the distribution of power users in certain areas,the sample data for residential electricity users,commercial power users and industrial power users are clustered.In connection with the actual electric consumption situation in the region,the load curve is analyzed.The area electricity characteristics and the results of the analysis of different kinds of power users are obtained.

fuzzy C-means clustering; K-means algorithm; load curve; electricity consumption behavior; characteristic analysis

10.3969/j.issn.1006-4729.2017.02.017

2016-09-08

余修成(1991-),男,在读硕士,安徽六安人.主要研究方向为智能电网电能供需优化与调控.E-mail:704913424@qq.com.

国家自然科学基金(61472236);上海市科学技术委员会地方能力建设项目(Z2014-076).

TP181;TM714

A

1006-4729(2017)02-0196-05