Polaron Effects on The Optical Absorption Coefficients in A Cylindrical ZnS/CdSe Core-Shell Quantum Dot

CHEN Zhi-hong, LI Qian-guang, YI Xu-nong, YU Hua-qing, XIONG Liang-bin

(SchoolofPhysicsandElectronic-informationEngineering,HubeiEngineeringUniversity,Xiaogan432000,China)

Polaron Effects on The Optical Absorption Coefficients in A Cylindrical ZnS/CdSe Core-Shell Quantum Dot

CHEN Zhi-hong, LI Qian-guang*, YI Xu-nong, YU Hua-qing, XIONG Liang-bin

(SchoolofPhysicsandElectronic-informationEngineering,HubeiEngineeringUniversity,Xiaogan432000,China)

The polaron effects on the linear and nonlinear optical absorption coefficients are investigated theoretically for electrons confined in a core-shell quantum dot. The interactions of electrons with the confined longitudinal optical (LO) and the interface optical (IO) phonon modes in the core-shell system are investigated. An analytic formula for the optical absorption is derived with compact-density-matrix approach and iterative method. The optical absorption coefficients in a ZnS/CdSe core-shell quantum dot (QD) are calculated numerically for different pump photon energies, incident optical intensities and relaxation times. Results show that the optical absorption coefficients are dependent on the photon energy and relaxation time dramatically. Moreover, when the electron-LO phonon interaction is considered, the optical absorption coefficient is enhanced more than 2 times.

polarons; core-shell quantum dot; optical absorption

1 Introduction

In recent years, much attention has been focused on the nonlinear optical properties of low-dimensional semiconductor structures[1-3], such as semiconductor quantum dot (QD). The quantum confinement of electrons in all three dimensions in QDs can result in the formation of discrete electron energy levels and the generation of a large number of linear and nonlinear optical phenomena compared with bulk semiconductors[4]. Recently，core-shell QDs with spherical symmetry have been the object of detailed experimental and theoretical investigations[5-6]. A core-shell QD is a nanometer structure with a “core” in its middle. Since it has considerable exceptional optical properties, core-shell QDs have attracted great interest in the physics and technological applications[7-8]. Hence， it is believed that a fundamental study on the optical properties of a core-shell QD is very important[9].

Among the electronic and optical properties in low dimensional structures, nonlinear optical properties are widely investigated, especially when optical absorption coefficients appeal to many researchers[10-13]. Zhangetal. studied the optical absorption coefficients and the variation of refractive index in parabolic quantum dots[10]. Yusuf Yakaretal. investigated the linear and nonlinear optical absorption coefficients of a spherical quantum dot with parabolic potential[11]. Yesilguletal. researched the effect of intense high-frequency laser field on the linear and nonlinear intersubband optical absorption coefficients and refractive index changes in a parabolic quantum well, considering applied electric field[12]. Gambhiretal. reported linear and nonlinear optical absorption coefficients and the variation of refractive index associated with intersubband transitions in a quantum disk with flat cylindrical geometry[14]. Their studies are concerned about optical absorption coefficients, and found that the optical absorption coefficients are strongly influenced by the impurity, incident optical intensity, relaxation time, and parabolic potential.

Meanwhile, many researchers have concentrated their attention on the effects of the electron-optical phonon interaction, especially in low-dimensional quantum systems[15-16]. Guoetal. reported the polaron effects on the third-harmonic generation for electrons confined in asymmetrical semi-exponential quantum wells[15]. They found that the third-harmonic generation is obviously increased when the electron-LO-interaction is taken into account. Mouetal. reported polaron effects on the linear and nonlinear intersubband optical absorption coefficients in quantum wells with asymmetrical semi-exponential potential[16]. The results of calculation show that optical absorption is enhanced when effects of polaron are considered. All research results have revealed that the electron-phonon interaction becomes more and more important in electronic properties and optical properties with the decreasing of the dimension.

However， there are few studies treating the electron-phonon interaction on the optical absorption in a core-shell quantum dot. Theoretically, this paper attempts to examine the linear and nonlinear optical absorption coefficients in a core-shell quantum dot taking polaron effects into account. The analytical expressions of the optical absorption coefficients are to be obtained by using density-matrix method and iterative method. In Section 3, the numerical results and some discussions are to be presented. A conclusion is drawn in Section 4.

2 Theory

2.1 Electron, Phonon and Electron-phonon Interaction Hamiltonian

The model considered in the paper is a suppositional core-shell cylindrical quantum dot with a centric barrier (ZnS) and a shell layer (CdSe), the outer space is filled with nonpolar medium: water, which can be treated as an infinite barrier, and the electromagnetic fieldE(ω)isparalleltotheZ-axis(shown in Fig.1 ).distheheightofthecylinder,andR1andR2aretheinnerandouterradii.

Undertheframeworkofeffective-massapproximation,theHamiltonian[17]ofthesystemcanbewrittenas

(1)

ThefirstterminEq. (1)istheHamiltonianofelectronHe, it is given by

(2)

Fig.1Modelofasuppositionalcore-shellcylindricalquantumdots

ThesecondtermisthefreephononHamiltonian:

(3)

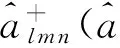
The last term of Eq. (1) stands for the electron-phonon interaction Hamiltonian:

(4)

He-LO1denotes the Hamiltonian of the electron interaction with LO phonon in the core[18]:

(5)

Jm(x) is the Bessel function of the first kind.xmlis themth zero ofJm(x).

Correspondingly,He-LO2is the Hamiltonian of the electron interaction with LO phonon in the shell[18]:

(6)

Tml(amlr/R1)satisfies the boundary conditions:

(7)

In Eq.(4), the last termHe-IOis the Hamiltonian of the electron interaction with IO phonon[18]:

(8)

2.2 Linear and Nonlinear Absorption Coefficients

The wave function of an electron in the core-shell quantum dot can be resolved from the Schrödinger equation of an electron[19]:

(9)

It is noted that the wave function above must satisfy the normalization condition. Besides, they must satisfy the boundary condition:

(10)

(11)

(12)

whereR<,R>standforthewavefunctionRfor the cases ofrR1.

Weassumethatthesystemwereinlowtemperature(T→0),sotheinitialstatewouldbethephononvacuumstate.Inthecourseofphonontransition,onlyone-phononabsorption(emission)isconsidered.Undertheframeworkofperturbationtheory,thesystemwavefunctioncanbewrittenas

whereε=ћωLOor ћωIO.

By using the compact density-matrix approach and iterative method, the optical absorption coefficients can be obtained. The electronic polarizationP(t) is formulated as

(14)

In our work, the optical absorption coefficients[10]can be expressed by

(15)

(16)

Thetotalabsorptioncoefficientisobtainedby

(17)

3 ResultsandDiscussion

TheopticalabsorptioncoefficientsinaZnS/CdSecore-shellcylindricalquantumdotarecalculatednumericallywithequation(17).TheparametersofZnSandCdSearelistedinTab.1[20].

Tab.1 Material parameters (m0is the rest electron mass) used in the calculation

Materialm*/m0ћωLO/meVћωTO/meVε0ε¥ZnS0.2843.633.678.15.14CdSe0.1326.4120.839.566.23

The conduction band discontinuity and electron density areVc=0.9 eV andN=5×1024m-3respectively in all calculations.

In Fig.2, the linear, third-order nonlinear and total optical absorption coefficients are plotted as a function of the photon energy ћω.TheincidentopticalintensityisI=0.5×1010W/m2,andtheparametersofthecore-shellcylindricalQDareR1=4.5 nm,R2=7.5 nm andd=4.0 nm. Two cases are analyzed using: electron-LO-phonon interaction effects and without electron-phonon interaction effects, which are illustrated by the dotted line and solid line, respectively. Judging from Fig.2, we can see that it is obvious that the large linear absorption coefficientα(1)ispositivewhereasthethird-ordernonlinearopticalabsorptioncoefficientα(3)isnegative.Sothetotalopticalabsorptioncoefficientαissignificantlyreducedbytheα(3)contribution.Therefore,thethird-ordernonlinearopticalabsorptioncoefficientα(3)shouldbeconsideredwhentheincidentopticalintensityIiscomparativelystrong,whichcaninducenonlinearabsorption.However,whenweconsidertheelectron-LOphononinteractioneffect,theopticalabsorptioncoefficientisover2timeslargerthantheoneinthecaseofnoconsiderationofthepolaroneffects,andthetotalopticalabsorptionwillbebleachedatcenterwithinthephotonenergy.Thematrixelementenhancesitselfbecauseelectron-phononinteractionmakesthewavefunctionoftheelectionspreadtowiderspace,whichenhancestheoverlapofwavefunctions.

Fig.2Linear,third-ordernonlinearandtotalopticalabsorptioncurvesfortwocases:consideringelectron-LO-phononinteractioneffectsandignoreelectron-phononinteractioneffects.

InFig.3,thelinear,third-ordernonlinearandtotalopticalabsorptioncoefficientsareplottedasafunctionofthephotonenergyћωwiththeincidentopticalintensityI=0.5×1010W/m2,R1=4.5 nm,R2=7.5 nm andd=4.0 nm for two cases: with electron-IO-phonon interaction effects and without electron-phonon interaction effects, which are illustrated by the dotted line and solid line, respectively. It can be shown that the electron-IO-phonon interaction effects on the optical absorption also make the linear absorption coefficient and the absolute value of third-order nonlinear absorption coefficient increase. Based on Fig.2 and Fig.3, we can also find that the influence of electron-LO-phonon interaction on the optical absorption is bigger than that of electron-IO-phonon interaction on the optical absorption. It shows that electron-LO-phonon interaction dominates the optical characters of electrons in low-dimensional system.

Fig.3 Linear, third-order nonlinear and total optical absorption curves for two cases: consider electron-IO-phonon interaction effects and ignore electron-phonon interaction effects.

In Fig.4, the total optical absorption coefficients are plotted as a function of the photon energy ћωwithτ=300fs,R1=4.5 nm,R2=7.5 nm andd=4.0 nm for the different values of incident light intensities. It can been seen from Fig.4 that the total optical absorption coefficient will reduce significantly with the increasing of the incident optical intensityIwhen the polaron effects (solid line) are ignored. We also can see that the total optical absorption

Fig.4 Total optical absorption curves for different incident light intensities. Two cases, with and without LO phonon, and three intensities,I=0, 1.0, 2.0×1010W/m2arepresented.

willbestronglybleachedwhentheelectron-LO-phononinteraction(dottedline)isconsidered.WhentheincidentopticalintensityIexceeds the value ofI=2.0×1010W/m2,thepolaronabsorptionpeakwillbesignificantlysplitupintotwopeaks,whichisinconsequenceofthebleachingoftheabsorptionatlinearcenter.

InFig.5,thetotalopticalabsorptioncoefficientsareplottedasafunctionofthephotonenergyћωwithτ=300fs,R1=4.5 nm,R2=7.5 nm andd=4.0 nm for two cases: electron-IO-phonon interaction effects and no electron-phonon interaction effects, which are illustrated by the dotted line and solid line, respectively. From Fig.5 we can see that the electron-IO-phonon interaction effects on the optical absorption also make the total optical absorption coefficient increase. From Fig.4 and Fig.5, we can also find that the influence of electron-LO-phonon interaction on the optical absorption is bigger than that of electron-IO-phonon interaction on the optical absorption.

Fig.5 Total optical absorption curves for different incident light intensities. Two cases, with and without IO phonon, and three intensities,I=0, 1.0, 2.0×1010W/m2arepresented.

InFig.6,thetotalopticalabsorptioncoefficientsareplottedasafunctionofthephotonenergyћωwithI=0.5×1010W/m2,R1=4.5 nm,R2=7.5 nm andd=4.0 nm for three different values of the relaxation timeτ=50, 100, 200 fs. We can see that the total optical absorption coefficient will increase significantly with the relaxation timeτincreasingwhenweignorethepolaroneffects(solidline).Wealsocanseethatthetotalopticalabsorptionwillincreasestronglywhenweconsidertheelectron-LO-phononinteraction(dottedline).

Fig.6Totalopticalabsorptioncuresfordifferentrelaxationtimes.Twocases,withandwithoutLOphonon,andthreerelaxationtimes,τ=50, 100, 200 fs are presented.

In Fig.7, the total optical absorption coefficients are plotted as a function of the photon energy ћωwithI=0.5×1010W/m2,R1=4.5 nm,R2=7.5 nm andd=4.0 nm for two cases: consider electron-IO-phonon interaction effects and ignore electron-phonon interaction effects, which are illustrated by the dotted line and solid line, respectively. From Fig.7, we can see that the electron-IO-phonon interaction effects on the optical absorption also make the total optical absorption coefficient increase. From

Fig.7 Total optical absorption cures for different relaxation times. Two cases, with and without IO phonon, and three relaxation times,τ=50, 100, 200 fs are presented.

Fig.6 and Fig.7, we can also find that the influence of IO phonon is smaller than that of LO phonon. In particular, the shift of total absorption peak is not distinct compared with that in Fig.6. Nevertheless, after considering the electron-IO-phonon interaction effect, the absorption peak is observed to become wider, which is remarkable like that in Fig.6. This verifies that polarization has a strong interaction with electromagnetic waves. Therefore, the polaron effect has a marked influence on the optical properties.

4 Conclusion

In this paper, we have researched the linear, third-order nonlinear, and total optical absorption coefficients of the weak-coupling optical polaron systems in the core-shell cylindrical quantum dots. The numerical calculations have been performed to study the total optical absorption coefficient of ZnS/CdSe core-shell cylindrical quantum dots by taking into account the influences of electron-LO-phonon and electron-IO-phonon interactions in this paper. The results show that the theoretical value of the optical absorption coefficient is greatly enhanced due to electron-phonon interaction effect. We also find that the influence of electron-LO-phonon interaction on the optical absorption is bigger than that of electron-IO-phonon interaction on the optical absorption. In addition, we find that the optical absorption coefficients are strongly affected by the incident optical intensity and the relaxation time. When the incident optical intensity becomes great enough the peaks of total optical absorption coefficients are split into two. Moreover, the correction of polaron effect to the energies of the electron makes the absorption peaks become wider. Therefore, the polaron effect has a marked influence on the optical properties.

[1] 于凤梅, 郭康贤, 谢洪鲸, 等. Morse势阱中子带间的光吸收 [J]. 发光学报, 2003, 24(3):247-252. YU F M, GUO K X, XIE H J,etal.. Intersubband optical absorption in Morse quantum well [J].Chin.J.Lumin., 2003, 24(3):247-252. (in English)

[2] 申继伟, 郭亨群, 吕蓬, 等. Si/SiNX超晶格材料的非线性光学特性 [J]. 发光学报, 2008, 29(6):1045-1049. SHEN J W, GUO X Q, LU P,etal.. Nonlinear optical properties of Si /SiNXsuperlattice [J].Chin.J.Lumin., 2008, 29(6):1045-1049. (in Chinese)

[3] 陈知红, 方天红, 李钱光, 等. 极化子效应对ZnS/CdSe柱型核壳量子点简并四波混频过程的影响 [J]. 光子学报, 2015, 44(4):0419003. CHEN Z H, FANG T H, LI Q G,etal.. Polaron effect on the degenerate four-wave mixing in a ZnS/CdSe quantum dot quantum well [J].ActaPhoton.Sinica, 2015, 44(4):0419003. (in Chinese).

[4] BOUZAIENE L, ALAMRI H, SFAXI L,etal.. Simultaneous effects of hydrostatic pressure, temperature and electric field on optical absorption in InAs/GaAs lens shape quantum dot [J].J.AlloysCompd., 2016, 655:172-177.

[5] LIU K, SCHMEDAKE T A, DANESHVAR K,etal.. Interaction of CdSe/ZnS quantum dots: among themselves and with matrices [J].Microelectron.J., 2007, 38(6):700-705.

[6] FENG X, XIONG G, ZHANG X,etal.. Third-order nonlinear optical susceptibilities associated with intersubband transitions in CdSe/ZnS core-shell quantum dots [J].PhysicaB:CondensedMatter, 2006, 383(2):207-212.

[7] 陈知红, 王军延, 方天红. 极化子效应对ZnS/CdSe量子点三阶极化率的影响 [J]. 发光学报, 2009, 30(4):535-540. CHEN Z H, WANG J Y, FANG T H. Effect of polaron effect on third-order susceptibility in ZnS/CdSe quantum dot quantum well [J].Chin.J.Lumin., 2009, 30(4):535-540. (in Chinese).

[8] NAIMI Y, JAFARI A R. Oscillator strengths of the intersubband electronic transitions in the multi-layered nano-antidots with hydrogenic impurity [J].J.Comput.Electron., 2012, 11(4):414-420.

[9] XIE W L. Absorption spectra and refractive index changes of an exciton in a core/shell quantum dot [J].Commun.Theor.Phys., 2015, 63(5):635.

[10] ZHANG C J, GUO K X. Polaron effects on the optical absorptions in asymmetrical semi-parabolic quantum wells [J].PhysicaE, 2007, 39(1):103-108.

[11] YAKAR Y, ÇAKIR B, ÖZMEN A. Calculation of linear and nonlinear optical absorption coefficients of a spherical quantum dot with parabolic potential [J].Opt.Commun., 2010, 283(9):1795-1800.

[12] YESILGUL U, UNGAN F, SAKIROGLU S,etal.. Effect of intense high-frequency laser field on the linear and nonlinear intersubband optical absorption coefficients and refractive index changes in a parabolic quantum well under the applied electric field [J].J.Lumin., 2014, 145:379-386.

[13] 于凤梅, 王克强, 申朝文. 极化子效应对非对称量子阱中光吸收系数的影响 [J]. 发光学报, 2010, 31(4):467-472. YU F M, WANG K Q, SHEN C W. Influence of polaron effects on the optical absorptions in asymmetrical quantum wells [J].Chin.J.Lumin., 2010, 31(4):467-472. (in English)

[14] GAMBHIR M, KUMAR M, JHA P K,etal.. Linear and nonlinear optical absorption coefficients and refractive index changes associated with intersubband transitions in a quantum disk with flat cylindrical geometry [J].J.Lumin., 2013, 143:361-367.

[15] GUO K X, XIAO B, ZHOU Y,etal.. Polaron effects on the third-harmonic generation in asymmetrical semi-exponential quantum wells [J].J.Opt., 2015, 17(3):035505.

[16] MOU S, GUO K, XIAO B. Polaron effects on the linear and nonlinear intersubband optical absorption coefficients in quantum wells with asymmetrical semi-exponential potential [J].Superlatt.Microstruct., 2014, 72:72-82.

[17] CHEN Z, YAO D, ZHANG X,etal.. Polaron effect-dependent third-order optical susceptibility in a ZnS/CdSe quantum dot quantum well [J].Microelectron.J., 2008, 39(12):1654-1658.

[18] XIE H J, CHEN C Y, MA B K. The bound polaron in a cylindrical quantum well wire with a finite confining potential [J].J.Phys.:CondensedMatter, 2000, 12(40):8623-8640.

[19] ZHANG X, XIONG G, FENG X. Well width-dependent third-order optical nonlinearities of a ZnS/CdSe cylindrical quantum dot quantum well [J].PhysicaE, 2006, 33(1):120-124.

[20] ALCALDE A M, MARQUES G E. Electron-optical-phonon scattering rates in spherical CdSe quantum dots in an external magnetic field [J].Phys.Rev. B, 2002, 65(11):113301.

陈知红(1980-)，女，湖北公安人，硕士，副教授，2007年于武汉大学获得硕士学位，主要从事非线性光学方面的研究。

E-mail: zhihong9905@163.com李钱光(1978-)，男，湖北广水人，博士，副教授，2010年于华中科技大学获得博士学位，主要从事飞秒激光脉冲与原子、分子相互作用的理论研究。

E-mail: liqianguang@126.com

2016-12-13；

2017-02-03

国家自然科学基金(11547018)； 湖北省教育厅研究项目(Q20142706)； 湖北工程学院自然科学基金(z2013028)； 湖北省自然科学基金(2014CFB579)资助项目 Supported by National Natural Science Foundation of China(11547018); Research Foundation of Education Bureau of Hubei Province(Q20142706); Natural Science Foundation of Hubei Engineering University(z2013028); Natural Science Foundation of Hubei Province(2014CFB579)

极化子效应对ZnS/CdSe核壳量子点光吸收系数的影响

陈知红， 李钱光*， 易煦农， 余华清， 熊良斌

(湖北工程学院 物理与电子信息工程学院， 湖北 孝感 432000)

在有效质量近似下，利用量子力学密度矩阵理论，从理论上研究了考虑极化子效应后核壳量子点中线性、三阶非线性以及总的光吸收系数在不同条件下随入射光能量变化的关系。通过数值计算，分析了电子-LO声子和电子-IO声子相互作用对ZnS/CdSe柱型核壳结构量子点光吸收系数的影响。结果表明，极化子效应对光吸收系数有很大影响，不同声子模式对光吸收系数影响大小不同。考虑电子-LO声子后，光吸收系数被大大提高。另外，入射光强和弛豫时间对系统的吸收系数也有很大影响。

极化子； 核-壳量子点； 光吸收

1000-7032(2017)05-0580-07

O437; O472.3 Document code： A

10.3788/fgxb20173805.0580

*CorrespondingAuthor,E-mail:liqianguang@126.com