等粒径球体三维体心立方堆积体接触力传递模型研究

张春光

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

等粒径球体三维体心立方堆积体接触力传递模型研究

张春光

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

基于等粒径球体三维体心立方堆积体的排列特点，提出了力均匀传递分配等五条基本假设，建立了竖向均布荷载作用下，等粒径球体三维体心立方堆积体中接触力竖向分量的计算模型，并利用该模型计算了相应堆积体中不同位置处的球体的接触力竖向分量，分析了堆积体内部接触力的理论分布规律。

三维体心立方堆积；接触力传递模型；接触力分布规律

0 引言

颗粒堆积体的研究及其工程应用是近年来多学科交叉发展研究起来的一门新兴学科，在路基填筑、堤坝填筑等工程技术研究中得到了较广泛的应用[1]。颗粒堆积体内部接触力的大小及分布规律决定着堆积体的宏观力学性能，由于堆积体中颗粒具有明显的离散性，传统的连续介质弹性理论在揭示堆积体中接触力分布规律方面适用性不足。因此探索研究荷载作用下颗粒堆积体中的接触力传递模型，对于揭示堆积体中接触力的分布规律，分析堆积体力学性能宏观表现的内在原因，解决堆积体实际工程问题有着重要的意义。

荷载在颗粒堆积体中的传递，可看作从堆积体顶层荷载作用位置出发，沿深度方向层层传递扩散的过程，荷载的传递规律与颗粒间的接触位置和接触状态有关[2]。本文基于静力平衡理论，结合堆积体中颗粒排列的特点，提出合理的假设，建立了竖向均布荷载作用下，三维体心立方堆积体中接触力的理论传递模型，并分析了堆积体中接触力的理论分布规律。

1 接触力传递模型研究现状简析

大量的堆积体接触力检测试验结果[3，4]表明，堆积体中接触力的峰值并非总是出现在外荷载作用线穿过的颗粒处，接触力存在双峰现象，且并非全部球体都分担外荷载，这与传统的弹性力学理论得到的结果不符。许多学者[5，6]从上述试验现象出发，探索了二维堆积体中接触力传递的理论模型。

刘建国[7]参考布辛涅斯克关于二维各向同性半无限线弹性体应力的推导成果，推导得到了颗粒在点荷载作用下的应力，并用光弹试验验证了推导结果。苏梁等[8]用解析法推导得到了外荷载作用下堆积体中的力链分布，并通过PFC2D模拟了双轴试验，在其他参数固定，仅改变应力水平的实验条件下，得到了相应的力链分布，发现二者结果定性吻合。

蒋红英[5，9]应用随机理论，将力的传递分为平均分配部分和波动量两部分，得到了二维紧密排列堆积体的竖向力的传递方程，定性地分析了相应排列方式下理想刚性颗粒堆积体中的底层接触力的变化规律。鲁进步等[9]应用随机理论，将颗粒间的力的传递特性分为等概率传递和单边偏移两种情况，建立了有序对称排列的二维颗粒堆积体中堆积体内部接触力的传递模型，并将该模型用于五层颗粒堆的力的传递分析，发现传递模型的理论分析结果与相应模型的光弹试验的实验结果定性吻合。

总体而言，堆积体中接触力传递的理论模型的研究，目前仍处于初级阶段，现有的理论模型尚不能同时定量和定性地解释堆积体中接触力的分布规律性[5]。

2 堆积体接触力传递模型

本文参考蒋红英[5，9]的研究成果，将力的传递部分分为平均分配部分和波动量两部分，并假设力波动量为零，提出了相应的基本假设，得到了如图1所示的等粒径球体三维体心立方堆积体中接触力的传递模型。

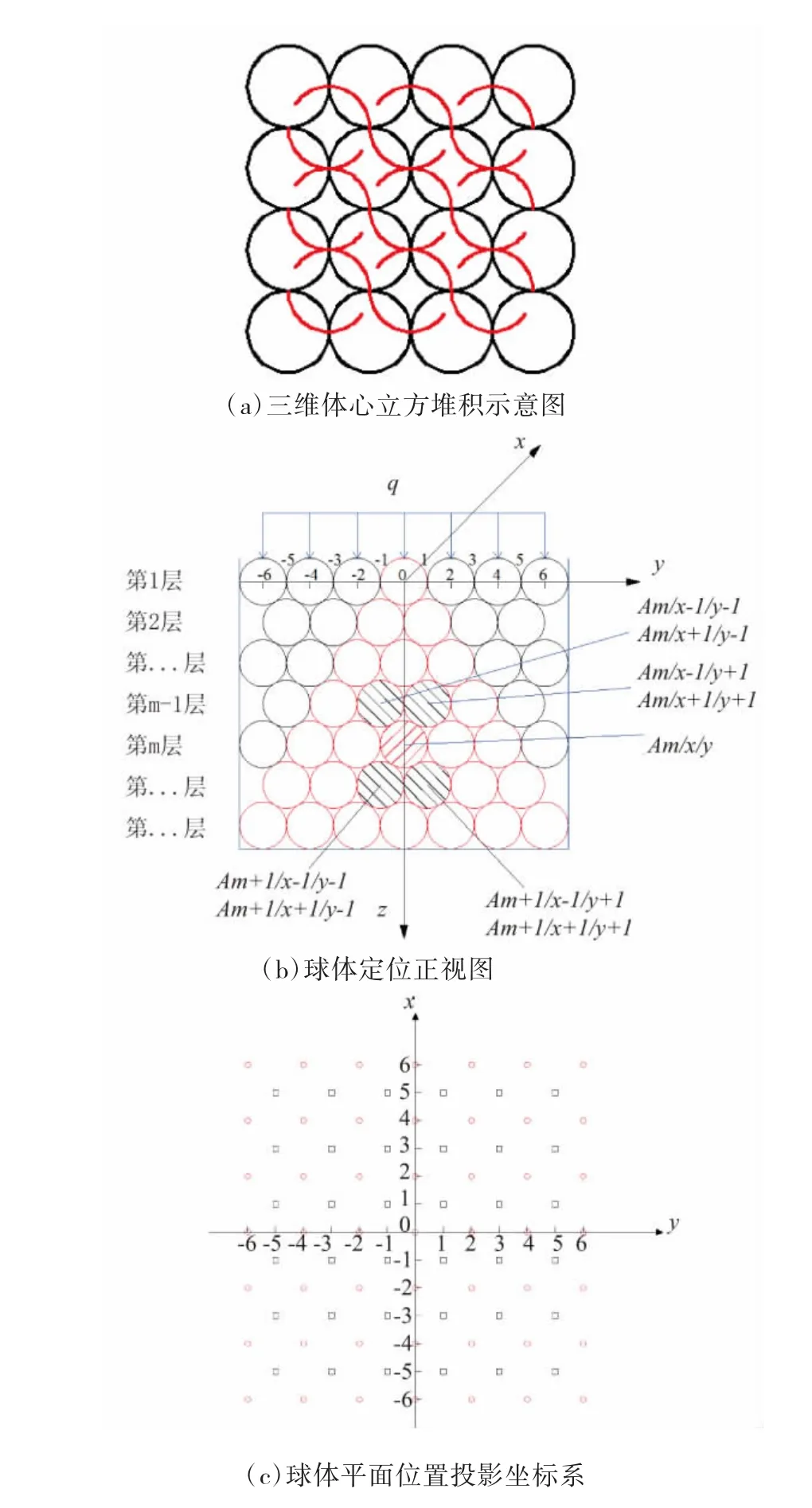
图1 竖向均布荷载作用下三维体心立方堆积体接触力传递模型推导示意图

图1中，Am/x/y表示第m层投影平面位置坐标为（x，y）处的球体，第m-1层中与Am/x/y球体紧邻的 4 个球体分别为 Am-1/x-1/y-1、Am-1/x-1/y+1、Am-1/x+1/y-1、Am-1/x-1/y+1，由此可以确定堆积体中任意位置处球体的编号。

2.2.1 基本假设

堆积方式不同，堆积体的空隙率、配位数等堆积状态参数也将不同，堆积体在荷载作用下的力学响应也会有所差别。

图1所示的三维堆积体中球体层间交错排列，荷载传递的同时伴随着扩散。参考文献[5]的研究成果，在建立堆积体接触力传递模型时提出以下基本假设：

（1）颗粒单元为等粒径球体；

（2）颗粒间接触位置处无切向力；

（3）只考虑竖向力的传递，横向力相互平衡；

（4）堆积体中远离边界处的单个球体受上层四个球体传递下来的力，且将力均匀传递给下层的四个邻近球体，紧邻边界处的球体将力均匀传递给下层邻近的一个或者两个球体；

（5）球体的位移和形变不改变力的传递路径。

2.2.2 堆积接触力传递模型的建立

由基本假设可知，图1所示的三维堆积体中，紧邻边界的球体所承担的竖向力分量只能完全分配给下层紧邻的一个球体或者两个球体，此时的力的分配比率为1或者1/2，其它位置处球体力的分配率均为1/4，由此可得均布荷载作用下三维体心立方堆积体中竖向力分量传递的通项公式，如式（1）所示：

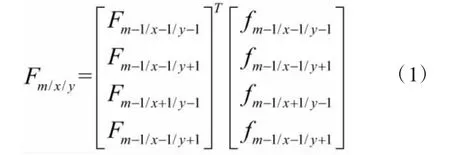
通项公式（1）即为等粒径球体三维体心立方堆积体，在理想堆积状态下（力波动量为零）的接触力竖向分量传递计算模型。

其中，fm-1/x-1/y-1为第 m 层中球体 Am-1/x-1/y-1的竖向力的分配比率；同理，fm-1/x-1/y+1、fm-1/x+1/y-1、fm-1/x-1/y+1为对应位置处球体的竖向力的分配比率。

显然，图1所示的三维堆积体中，存在如图2所示的两种层间关系：

根据通项公式（1），从堆积体顶层开始推算，首先对同一层中接触力竖向分量呈现相同分布规律的进行分类，然后将其代入图2所示的层间关系图，可得如图3所示的层间传递计算过程图，便可推算得到下一层不同位置处球体所承担的竖向力分量。基于此，便可逐层计算得到三维体心立方堆积体中不同位置处球体的接触力竖向分量。

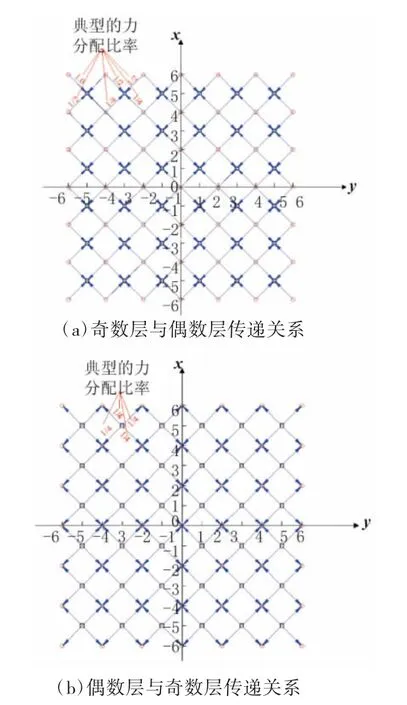
图2 堆积体层与层之间的传递关系

图3 层间传递计算图（第2层传递给第3层）

3 接触力理论分布规律

将上述接触力传递模型用于计算规模为“7×7—6×6”（即奇数层球体数量为7×7，偶数层球体数量为6×6）的等粒径球体三维体心立方堆积体的接触力，竖向均布荷载作用下堆积体中不同层位、不同位置处球体的接触力竖向分量，计算结果见图4。

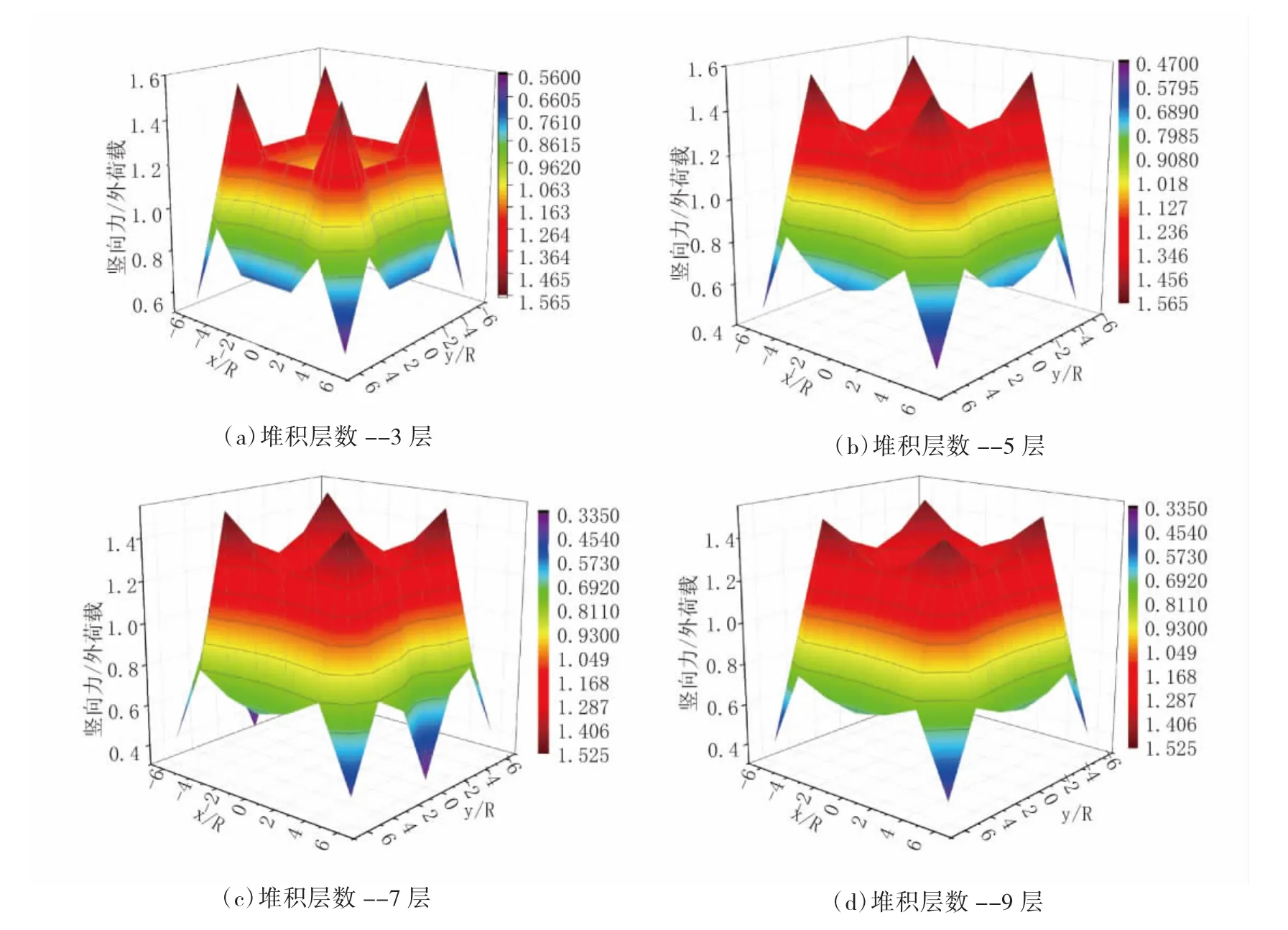
图4 堆积体竖向力分量的理论计算结果

由图4可得，“7×7—6×6”规模的堆积体中3、5、7、9层中不同位置球体的竖向力分量均呈现以x轴、y轴和z轴为对称轴的轴对称分布规律。竖向力分量呈现中心区域小，其他区域大的“中心区域凹陷”的现象，且随着堆积层数的增加，“中心区域凹陷”的趋势变缓，接触力大小分布渐趋均匀。此外，不同位置球体的竖向力分量均在空间4个对称的位置出现4个等大的峰值，且峰值出现的位置不随堆积层数的增加而改变，峰值随着堆积层数的增加减小。

4 结语

本研究建立了竖向均布荷载作用下，等粒径球体三维体心立方堆积体中接触力竖向分量的计算模型，利用该模型计算得到了相应堆积体中不同位置处的球体的接触力竖向分量，发现竖向力分量整体呈现中间区域小、其他区域大的“中间区域凹陷”规律，且在4个固定位置出现4个等大峰值；随着堆积层数的增加，“中间区域凹陷”的趋势减变缓，峰值也逐渐减小。

[1]蒋红英,鲁进步.颗粒堆中轴向静荷载力传递实验分析[J].兰州理工大学学报,2006(5):2-3.

[2]BOUCHAUD J P,CLAUDIN P,LEVINE,etc.Force chain splitting in granular materials:A mechanism for large-scale pseudo-elastic behavior[J].Eur Phys J E,2001(4):451-457.

[3]刘源,缪馥星,苗天德.二维颗粒堆积体中力的传递与分布研究[J].岩土工程学报,2005(4):2-6.

[4]蒋红英,鲁进步.颗粒堆中轴向静荷载力传递实验分析[J].兰州理工大学学报,2006(5):2-3.

[5]蒋红英.颗粒介质传力特性及其在岩土工程中的若干应用问题[D].甘肃兰州:兰州大学,2005.

[6]GOLDENBERG C,GOLDHIRSCH I.Force chains,micro-elasticity and macro-elasticity[J].Phys Rev Letters,2002,89(8):1-4.

[7]刘建国.颗粒物质局部化行为的细观研究[D].北京：清华大学, 2013.

[8]苏梁,苏强,马良荣.解析法推导颗粒体系在受理过程中的力链分布[J].山西建筑,2011(9):1-2.

[9]蒋红英,苗天德,鲁进步.二维颗粒堆中力传递的一个概率模型[J].岩土工程学报,2006(7):2-5.

U416.1

A

1009-7716（2017）04-0202-03

10.16799/j.cnki.csdqyfh.2017.04.059

2017-02-27

张春光（1966-），男，上海人，工程师，从事道路交通设计工作。