一种新的正交异性壳体单元有限元列式及其应用

张 慧，刘世忠，蔺鹏臻,冀 伟

（1.兰州交通大学甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070；2.兰州交通大学土木工程学院，甘肃 兰州 730070）

一种新的正交异性壳体单元有限元列式及其应用

张 慧1,2，刘世忠1，蔺鹏臻1,冀 伟1

（1.兰州交通大学甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070；2.兰州交通大学土木工程学院，甘肃 兰州 730070）

针对土木工程普遍采用的正交异性壳体结构，按照刚度等效的原则，推导出一种新的材料正交异性壳体单元有限元列式。编制了有限元计算机程序，通过输入结构参数可将正交异性壳单元换算为均匀厚度的壳单元。以某大宽跨比正交异性钢箱梁桥为例，通过精细有限元模型、大比例模型试验以及算法的对比分析，结果表明该算法可满足工程初步设计要求，从而节省了结构工程师大量的有限元建模、后处理的工作量。该方法可纳入通用位移法有限元程序，简化结构设计过程。

正交异性板；壳单元；模型试验；有限元方法；箱梁

0 引言

为适应交通现代化的发展需求，一些高速公路桥梁开始向8车道发展，单幅桥梁的横向宽度不断增加。国内外建造的连续梁桥中采用能适应较宽桥梁的大宽跨比、宽体、单箱多室宽箱截面形式者越来越多，部分桥梁的宽度已经接近或者相等于跨度。这种桥梁具有抗扭刚度大、腹板间距大、横向翼缘宽、箱壁薄等特点。薄壁箱梁从刚度、强度、经济考虑和减轻自重方面均被认为是一种有效的结构形式[1]。正是基于以上特点，普通梁理论已不再适用于这种桥梁结构的分析计算，哪怕是初步设计阶段也必须采用空间分析以拟定结构构件的主要尺寸[2-9]。

尽管精细的有限单元模型使得正交异性板薄壳箱梁的分析不再是结构分析的难题，然而理论分析对于设计计算过程中（尤其是初步设计过程中）快速准确地确定内力和弯矩仍然是一种非常有效的方法，但有限元模型建立以及后期处理工作量十分巨大而未被工程师采用。

对于正交异性结构，传统的解析分析方法是把它分成三个结构体系加以研究[10]，但是，对于顶板底板、翼缘板和腹板均为正交异性板的钢箱梁结构上述分析方法过于复杂，在实际应用上面存在困难。因此，有必要找到一种适合于此类结构有效的简化计算方法，将设计人员从初步设计阶段开始就从繁重的有限元建模、冗长的后处理工作中解放出来。

本文以一大宽跨比正交异性板鱼腹式箱梁桥为研究对象[11-13]。通过构造一种新的材料正交异性薄壳单元有限元列式，找到将复杂正交异性壳换算为均匀薄壳的简化途径，并利用计算机编程实现数值计算。通过输入计算参数，将正交异性壳单元转化为类似等厚度壳同样的壳单元。通过建立大比例模型试验，对比试验测试数据、精细的有限元模型计算数据和本文算法的计算结果。结果表明：本文算法简单易行，可极大地节省工作量，精度满足工程要求。研究成果将对提高我国结构工程科技水平具有积极的意义，并且将会产生很好的社会及经济效益。

1 分析方法

虽然钢材本身是一种各向同性材料，通常桥梁结构的一块弹性的正交异性板（如顶板）是由纵横向加劲肋刚度不同形成的，从而形成了一种结构上的正交异性薄壳。本文构造一材料正交异性薄壳，按照刚度等效原则，将复杂正交异性壳换算为均匀薄壳，见图1。本文所构造的加劲肋采用了最简单的一字型形式，对于其他形式的加劲肋（如T型、U型和L型等）也同样适用。

对于等厚薄壳结构的分析可按照两类问题来进行分析。但是经典的弹性理论和有限元列式的推导是基于材料的各项同性展开的，而本文构造的薄壳为材料正交异性，所以原有的方法已经不再适用。需要按照正交异性材料的应力应变关系重新推导。

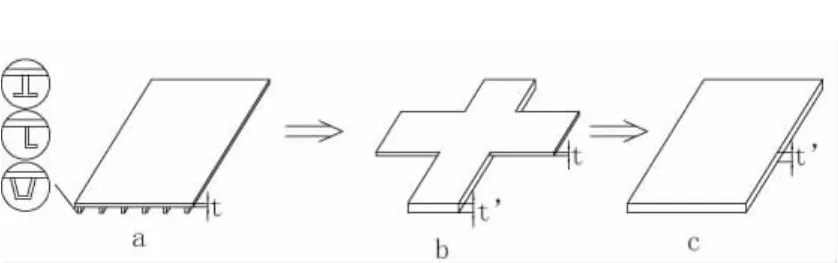
图1 转换过程图

2.1 平面应力问题

根据广义胡克定律，设原正交异性薄壳厚度为（见图1（a））。假定横梁的影响忽略不计。保持拉压刚度不变，加劲肋均匀分摊形成一块厚度为（见图1（c））的材料正交异性薄壳。令Ex=E、μx=μ，则。E，μ是原结构弹性模量和泊松比。可推导出平面应力问题的单元刚度矩阵为一个8×8的行列式。

1.2 薄板弯曲理论

本文以薄板的小挠度弯曲理论为基础，在满足基本假定条件的条件下，设原正交异性薄壳厚度为（见图1（a））。保持抗弯刚度不变，将纵向加劲肋换算后的薄壳厚度为h。令Ex=E、μx=μ，则可推导出薄板弯曲问题的单元刚度矩阵为一个12×12的行列式。其中

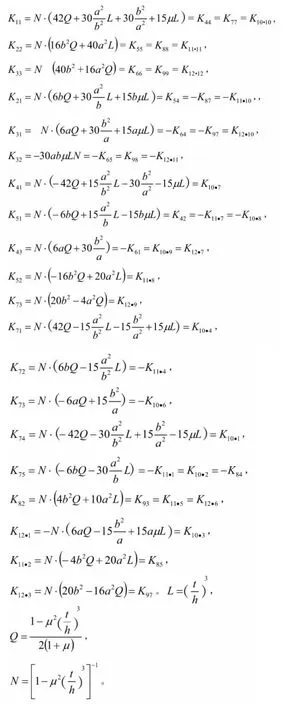
可将两个刚度矩阵扩阶叠加，形成总的单元刚度矩阵，不再赘述。

在推导出新的材料正交异性壳体单元有限元列式之后。编制有限元计算机程序，通过输入结构参数可将正交异性壳单元换算为均匀厚度的壳单元。

2 计算

2.1 算例

2.1.1 算例一——平面应力问题

本文以一个算例对平面应力问题的位移计算结果进行分析。

如图2所示一块边长6 m的正方形板，一边固定，一边施加均布荷载2 kN/m2，材料参数E= 2 MPa,。对此结构分别按照构造正交异性即精细有限元法（算法1）和换算之后的材料正交异性（算法2）两种情况分别计算，见表1。

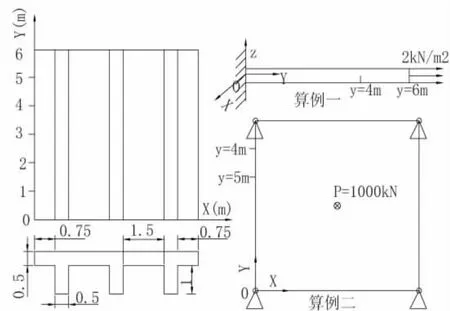
图2 正交异性板（单位：m）

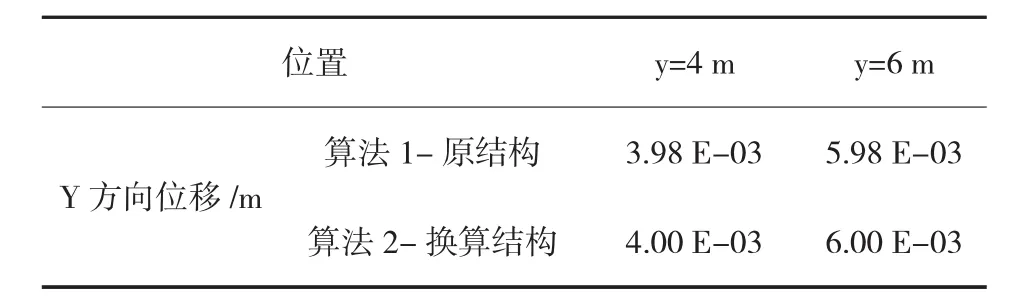
表1 计算结果表

2.1.2 算例二——薄板弯曲问题

仍以图2为例，将一边固定改为四边简支，在板的中心施加集中荷载P=100 kN，材料参数不变。对此结构分别按照构造正交异性即精细有限元法（算法1）和换算之后的材料正交异性（算法2）两种情况分别计算。提取出y=4 m和y=5 m两个截面的最大位移值，见表2。

表2 计算结果表

上述两个算例的计算结果表明，本文计算方法的近似程度在位移上可以满足工程需要。

2.2 实例应用

本文参照厦门市仙岳路跨路口高架钢箱梁桥制作了1∶8的大比例有机玻璃试验模型，桥式结构为一单箱五室的薄壁钢箱连续梁桥。模型梁桥跨布置为：4.5 m+4.5 m的2跨箱形连续梁。全桥共设置9个横隔板。支座位于梁的两端和中间支点处，每排对称布置两个。采用的有机玻璃板的厚度有：1 mm、1.5 mm、1.8 mm、3.5 mm四种类型。材料试验的拉伸试验采用制作模型的同一批材料来进行。经过测量和计算，得到试验模型的弹性模量E=2.65 GPa，泊松比μ=0.350 5[14]。根据04规范公路车道荷载，按照集中荷载和分布荷载的相似比例对试验荷载进行计算，见表3。位移测点见图3。

表3 加载图示

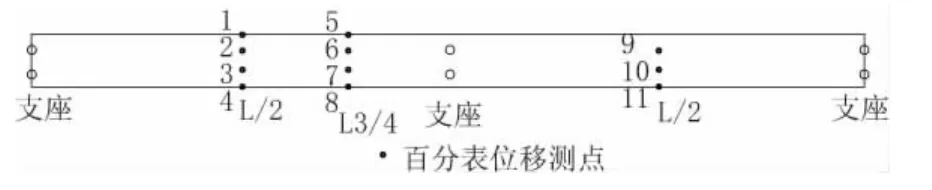
图3 位移测点布置图

从表4中可以看出，在位移计算中，本文算法与精细有限要模型计算结果吻合较好。说明该算法的计算结果的有效性，能够用于桥梁结构的解析分析中。试验结果偏大，这主要是由于模型材料的不均匀和测试误差造成的。此外有机玻璃的粘接会在一定程度上降低有机玻璃的弹性模量，这也会造成试验结果与计算之间的偏差。

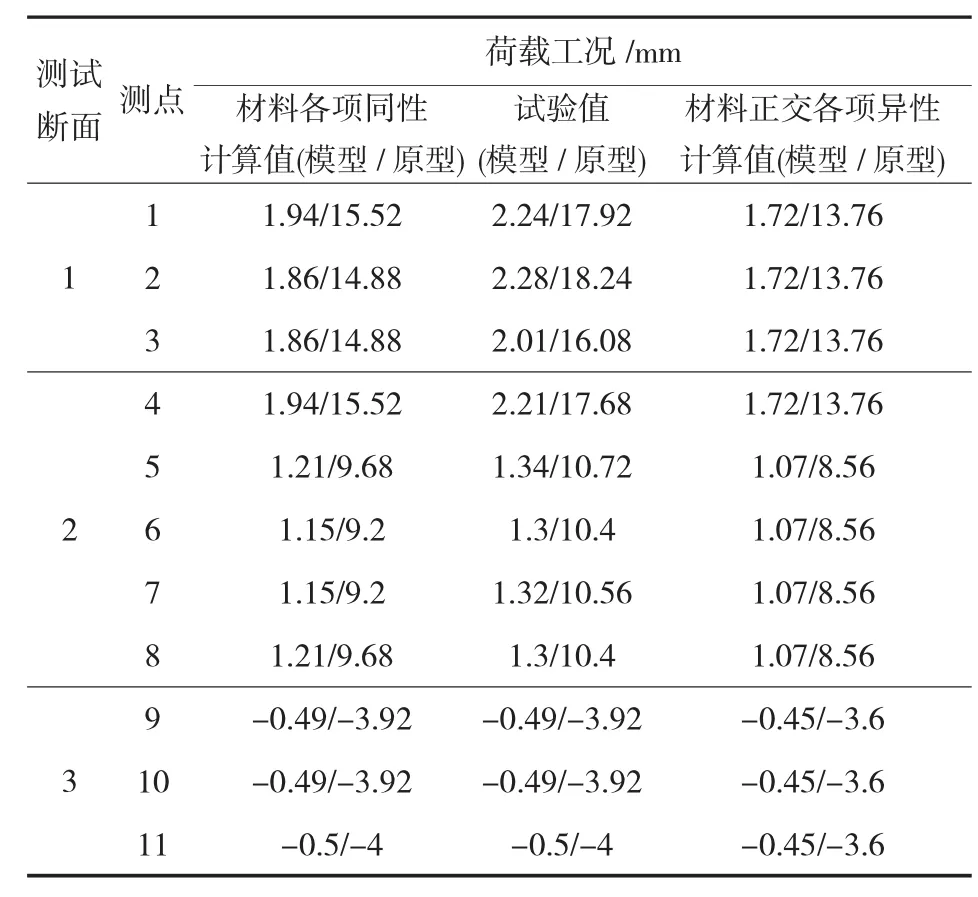
表4 荷载作用下测试断面挠度值和有限元计算值比较 mm

左跨L/2截面的顶底板正应力分布的计算值和试验值见图4。从图4中可以看出精细的有限元模型与测试结果吻合良好。在应力分布的计算中，本文算法与前面两者无论在数值还是分布趋势上均比较接近，但是存在少许偏差。虽然以刚度等效的计算原则对位移计算结果控制较好，但由于荷载加载位置和结构纵横隔板的局部效应的影响，会对应力计算产生一定的误差。由图4中的计算结果可以看出，虽然存在少量偏差，但仍然能满足工程要求。图5所示截面位于左胯3/4处，其应力分布情况和截面一类似。

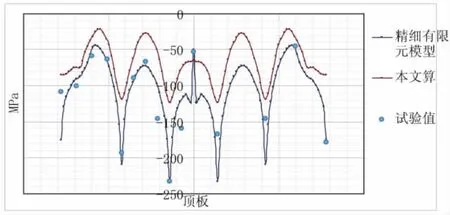
图4 左跨L/2截面应力分布

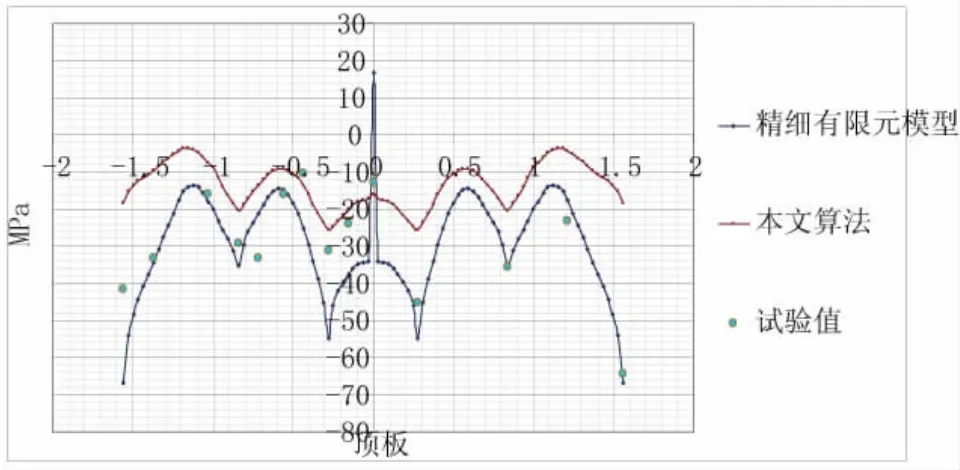
图5 左跨3L/4截面应力分布

3 算法比较

由表5可以看出精细有限元模型建模时间长，求解规模大，对细部结构的建模花费了大量的时间。本文算法比传统精细模型计算工作量大幅度减少，但仍然满足工程要求。以此类推，如果模型较复杂的时候，无论在建模时间和计算工作量上都能大大地节约，从而起到了简化模型的目的。

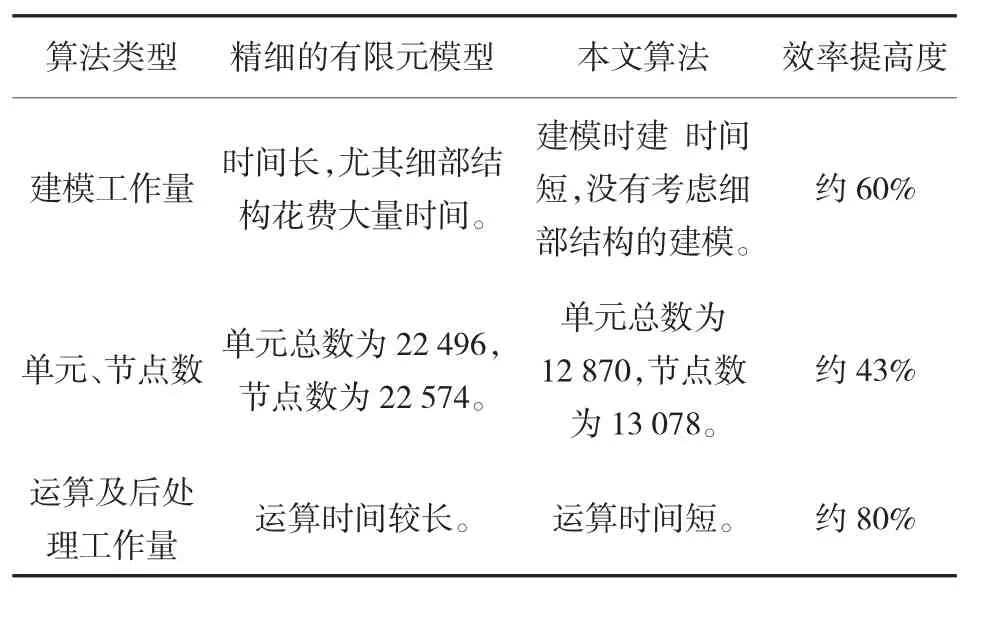
表5 本文算法与精细有限元模型工作量比较

4 结论

本文推导出一种新的材料正交异性壳体单元有限元列式并编制了有限元计算机程序。以某大宽跨比正交异性钢箱梁桥为例，通过精细有限元模型、大比例模型试验以及本文算法的对比分析，结果表明本文算法可满足工程要求并节省了大量的有限元建模、后处理的工作量。本文方法可纳入通用位移法有限元系统，具有广泛的工程应用前景。

[1]Vlasov VZ.Thin-walled elastic beams[Z].Washington,DC:National Science Foundation,1961.

[2]罗旗帜,娄奕红,杜嘉斌,等.变高度连续曲线箱梁的剪力滞效应[J].铁道学报,2007(5):79-84.

[3]王慧东,强士中.压弯荷载下薄壁箱梁剪力滞效应的变分解[J].北京工业大学学报,2008,32(11):982-987.

[4]程翔云,罗旗帜.箱梁在压弯荷载共同作用下的剪力滞[J].土木工程学报,1991,24(1):52-64.

[5]韦成龙,李斌,刘小燕.分离式双肋截面主梁剪滞效应分析的传递矩阵法[J].桥梁建设,2008(2):31-37.

[6]卜铭,胡贤成,田仲初,等.具有单横坡的箱梁剪力滞效应分析及试验研究[J].中外公路,2008,27(1):104-107.

[7]郝超,张杰,裴岷山.大跨度钢斜拉桥流线形扁平钢箱梁中纵隔板作用分析[J].中南公路工程,2002(4):45-47.

[8]苏庆田,吴冲,董冰.斜拉桥扁平钢箱梁的有限混合单元法分析[J].同济大学学报(自然科学版),2009(6):742-746.

[9]曾明根,苏庆田,吴冲.大跨斜拉桥扁平钢箱梁受力计算[J].桥梁建设,2007(3):17-20.

[10]Pelikan W,Esslinger M.Die Stahlfahrbahn–Berechnung and Kons truktion[J].M.A.N.Forschungsheft,1957(7).

[11]Hui Zhang,R.DesRoches,Zijiang Yang,tec.Experimental and analy tical studies on a streamlined steel box girder[J].Journal of Construc tional Steel Research,2010(66):906-914.

[12]Hui Zhang,Zijiang Yang,Shizhong Liu.Simplified analysis of longitu dinal stiffened plates in a continuous steel box girder bridge[J]. Applied Mechanics and Materials,2012(5).

[13]Hui Zhang,Zijiang Yang,Shizhong Liu.Different Simulation Methods in Thin-walled SteelBox Girder [A].The 4th International Symposium on Lifetime Engineering of Civil Infrastructure[C].2009.

[14]张慧,杨子江.大悬臂鱼腹式薄壁钢箱梁模型试验研究[Z].甘肃兰州:兰州交通大学,2009.

TU375.4

A

1009-7716（2017）04-0198-04

10.16799/j.cnki.csdqyfh.2017.04.058

2017-02-17

国家自然科学基金 (Grant No.50968008)；兰州交通大学青年基金(Grant No.2011035)；长江学者和创新团队发展计划资助(IRT1139)；甘肃省道路桥梁与地下工程重点实验室基金

张慧（1979-），女，甘肃兰州人，副教授，从事桥梁结构教学研究工作。