基于搜索算法的太阳影子变化建模

刘婵 江伟

摘 要：如何确定视频的拍摄地点和日期是视频数据分析的重要方面。本文旨在2015年数学建模A题数据资料前提下建立基于搜索算法的太阳影子变化模型。首先通过建立地平坐标系，利用太阳高度角和太阳方位角来定位太阳的影子，并联立太阳高度角，太阳方位角，赤纬角，时角等的计算公式，得到影子长度的变化模型一，使用MATLAB软件编程求解模型，计算出影子长度以及变化的曲线图。然后对数据进行分析发现影子的长度是先减小后增大，在11时44分达到最小值3.8411m，在15时达到最大值7.7393m，太阳高度角则先增大后减小并与影子长度呈相反的增长过程，影子长度最短时太阳高度角达到最大值37.991°，影子长度最长时达到最小值21.1878°，而太阳方位角则随时间增长而变大，最后对影子长度的变化曲线图进行了拟合，误差（MSE）不超过10-2。

关键词：太阳影子；太阳高度角；太阳方位角；MATLAB

1 问题的提出与分析

确定视频的拍摄地点和拍摄日期是视频数据分析的一个非常重要的技术，太阳影子定位技术就是通过分析视频中物体的太阳影子变化规律来确定视频拍摄的地点和日期的一种方法。如何建立影子长度变化的数学模型来计算出某固定地点直杆太阳影子的变化曲线，并找到影子长度关于各个参数的变化规律。

由于太阳和地球半径差别很大，故在可假定地球是一个球体，位置不动，仅仅考虑太阳公转来建立地平坐标系，根据公式的推导借助软件计算影子的长度以及画出曲线图并分析。

2 定义与符号说明

3 模型的建立与求解

3.1 模型假设

1）地球自转忽略不计，仅考虑地球公转。

2）地球为规则球体。

3）附件数据真实无误差。

3.2 地平坐標系的建立

尽管地球绕着太阳运行，但由相对运动，在地球上看却是太阳在天空中运动。为了精确描述太阳在天空中的运动和位置，由于太阳和地球半径差别很大，故在本文中假定地球是一个球体，位置不动，仅仅考虑太阳公转来建立地平坐标系，以地平面为xoy平面，以直杆底端的端点为原点，以直杆的方向为z轴，这样就可以用太阳高度角和太阳方位角来确定太阳天空中所处的位置，如下图所示：

其中xoy面表示地平面，原点o为直杆底部顶点，h为太阳高度角（即太阳直射光线与地平面间的夹角），A为太阳方位角（即太阳直射光线与地平面正北向所夹的角）。

3.3 分析与建模

模型的分析和建立分为以下几个步骤：

3.3.1太阳高度角h的计算

其中，

φ表示纬度，即某点与地球球心的连线和地球赤道面所成的线面角，其数值在0至90度之间；

δ表示太阳赤纬角，即地球赤道平面与太阳和地球中心的连线之间的夹角；

Ω表示时角，即在地球赤道平面上的投影与当地时间12点时、地中心连线在赤道平面上的投影之间的夹角。

3.3.2太阳方位角A的计算

其中δ表示太阳赤纬角；Ω表示时角。

3.3.3太阳赤纬角δ的计算

其中n表示积日，例如从2015年1月1日到2015年10月22日之间的积日n=295天。

3.3.4时角Ω的计算

其中真太阳时ST=北京时间t+时差，时差=（120-当地经度）/15。

3.3.5影长与直杆长度的关系

图一中直杆的高度为H=3m，太阳影长为L，满足如下关系式：

3.3.6太阳影子投影分量之间的关系

影子长度在x、y轴方向上的投影分别为x、y，则有：

将以上（1）至（6）式联立，可建立由当地时间、经度、纬度计算太阳影子长度的模型一，如下所示：

3.4 模型的求解

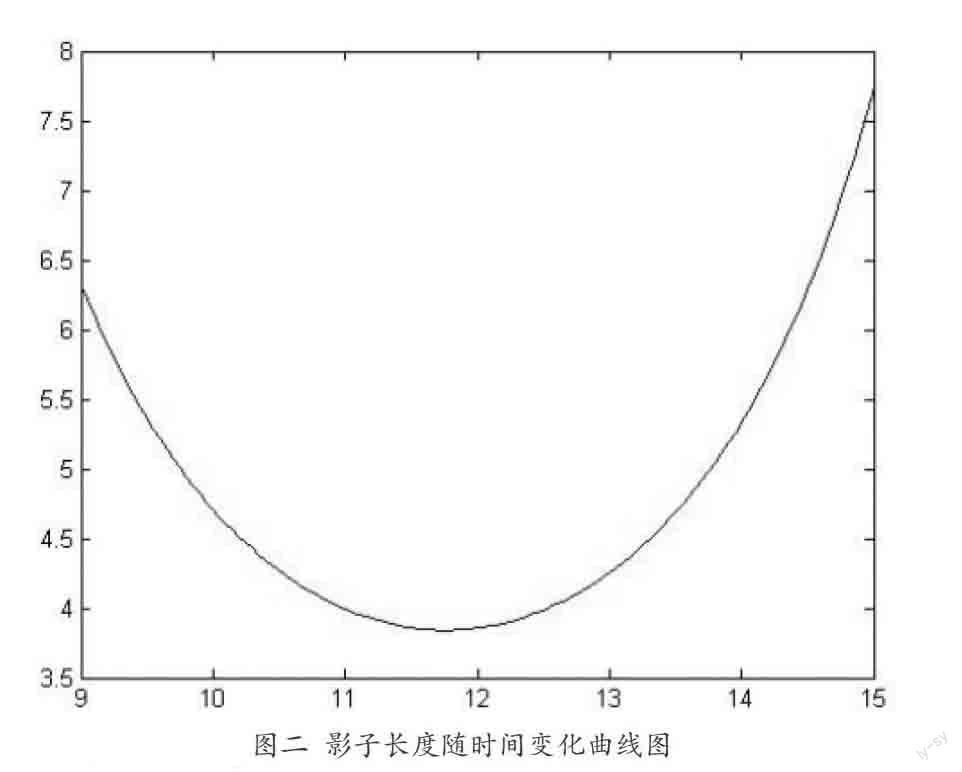
将2015年10月22日9：00——15：00这一时间段按3分钟为单位进行划分（参考了附件中时间的划分方式），通过如下MATLAB程序对模型一进行求解（软件版本号为7.0.1.），画出随时间变化的影子长度图如下图所示：

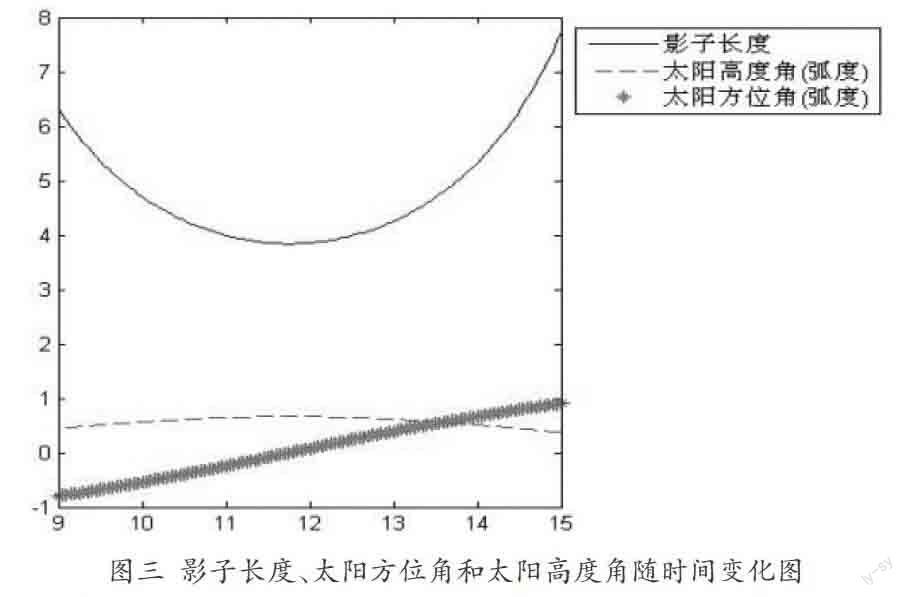
为了便于分析各个参数对影子长度的影响，同时将太阳高度角和太阳方位角随时间变化的曲线与图二曲线放在一起进行分析：

从图三很容易观察到：随着时间的推移，影子的长度是先减小后增大，在11时44分达到最小值3.8411m，在15时达到最大值7.7393m，太阳高度角则先增大后减小并与影子长度呈相反的增长过程，影子长度最短时太阳高度角达到最大值37.991°，影子长度最长时达到最小值21.1878°，而太阳方位角则随时间增长而变大。

3.5 影子长度曲线拟合

从图三可以看出，由影子的轨迹图像，关于最低点是左右对称的，从以下的影子轨迹线形成图四中也可以观察出来，也就是说影子的轨迹图像与某个抛物线的形状很接近，因此，可对影子曲线轨迹进行二次函数拟合。

以时间t为自变量，以影子长度为因变量，使用MATLAB程序对影子曲线图进行二次函数拟合，得出拟合函数为：

拟合图如下所示：

由于样本数量较多，故在误差估计时计算的是均方差的数值，均方差（MSE）=8.9*10-3，拟合效果较好。

l（t）是一个抛物线，关于时间11时45分对称，即为拟合出的当地正午时间，与图二的真实正午时间相差一分钟，说明拟合的效果比较好，符合实际情况。

参考文献：

[1] 郑鹏飞，林大钧，刘小羊，吴志庭.基于影子轨迹反求采光效果的技术研.自然科学版，2010，8.

[2] 王国安，米鸿涛，邓天宏，李亚男，李兰霞.太阳高度角和日出时刻太阳方位角一年变化范围的计算.气象与环境科学，2007，9.

[3] 汪晓银，周保平.数学建模与数学实验.科学出版社，2012，8.

通讯作者：江伟