电力系统元件非线性微分—代数子系统模型的逆系统控制：一种新算法

臧强 胡凯 陈炜峰 郑柏超 杨莹 杨卫诚

摘要 針对电力系统元件非线性微分-代数子系统模型，本文提出一种新算法研究其逆系统控制问题.所提出的新算法不需要对控制输出及其高阶导数做复杂的变换，具有更好的应用性.本文的逆系统控制方法主要分为两步：第1步，利用所提出的新算法来判断被控元件的可逆性，若可逆，则基于状态反馈与动态补偿，构造出元件的α阶积分右逆系统，实现复合系统的线性化和解耦；第2步，利用线性控制的理论和方法设计闭环控制器，使得元件被控对象满足期望的性能指标.最后按照本文所提出的方法，研究了多机电力系统的分散非线性汽门控制问题.仿真结果验证了本文所提方法的有效性.

关键词 电力系统；元件；微分-代数子系统；逆系统

中图分类号TP13

文献标志码A

0 引言

近年来，对于电力系统非线性微分-代数（Differential-Algebraic Equations，DAE）系统模型的研究取得了很大进展.文献[1]将非线性常微分方程（Ordinary Differential Equations，ODE）系统的Lyapunov方法进行了扩展，给出了非线性DAE系统稳定的充分条件，并将其应用于电力系统的稳定性分析；文献[2]给出了非线性DAE系统的精确反馈线性化方法，并用于解决带有非线性负荷的电力系统控制问题.而进一步的研究表明，电力系统元件模型本质上是指数1且关联可测的非线性DAE子系统模型，与电力系统其余部分存在相互约束，受电力系统其余部分产生的“关联输入变量”的影响[3].针对基于上述DAE子系统模型的电力系统元件，文献[4]系统地讨论了其系统特性，并给出了研究其控制问题的一般性思路；文献[5]研究了其非线性反步控制方法，实现了闭环系统的渐近稳定；文献[6]则研究了电力系统DAE模型的降阶问题，使等价模型更适合于控制器设计.

在各种非线性控制方法中，逆系统方法不需要进行复杂的坐标变换，过程简单明了，物理意义清晰且适用于一般非线性系统，在系统的线性化、解耦等控制问题的研究中具有重要的地位[7].文献[8-9]提出了一种所谓的“递归算法”，用以判断电力系统元件非线性DAE子系统的可逆性问题.然而该算法需要在每一步对控制输出及其高阶导数做复杂的变换，若系统输出维数较高，该算法的复杂性将显著增长，应用性不强.

针对电力系统元件非线性DAE子系统模型，本文提出一种新算法，来研究其逆系统控制问题.与文献[8-9]的结果相比，本文所提出的新算法不需要对控制输出及其高阶导数做复杂变换，更易于计算，应用性更强.本文主要内容安排如下：首先对电力系统元件非线性DAE子系统模型的系统特性进行了描述，同时给出了非线性DAE子系统的α阶积分右逆系统定义；然后给出新算法，以判断被控元件的可逆性，若元件可逆，则构造出物理可实现的逆系统，实现复合系统的线性化解耦；最后利用本文所提出的控制方法，研究了多机电力系统的分散非线性汽门控制问题并进行了仿真，仿真结果验证了本文所提方法的有效性.

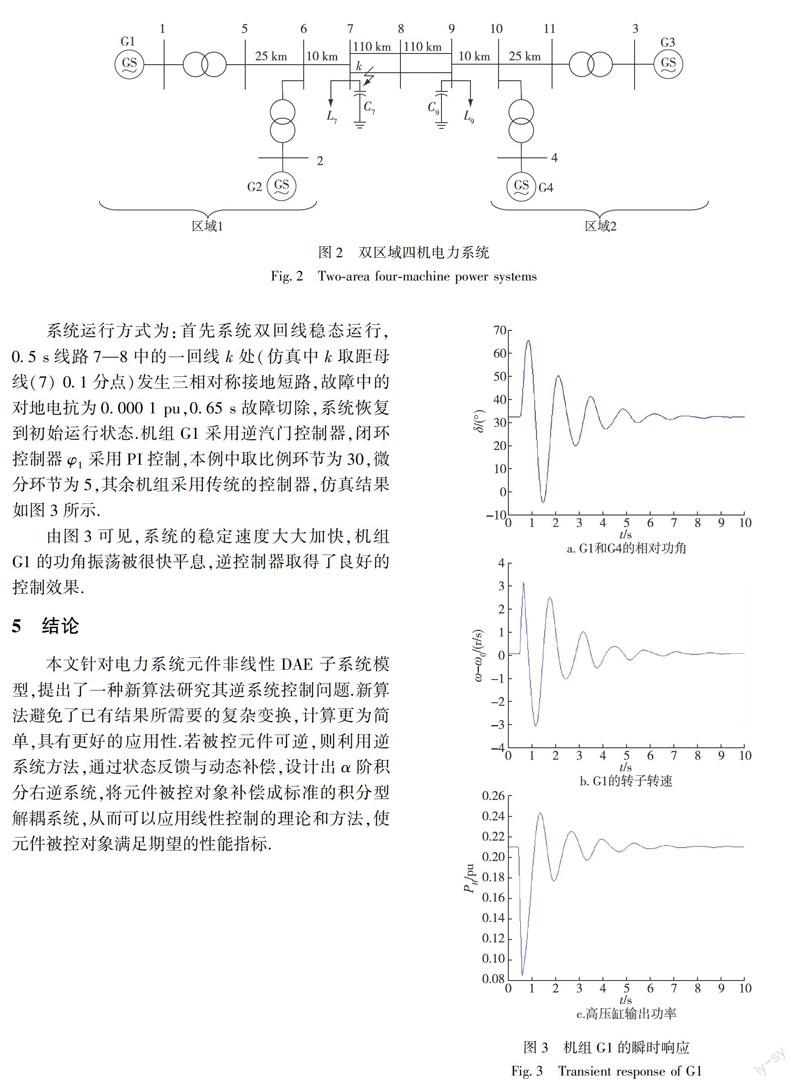
系统运行方式为：首先系统双回线稳态运行，0.5 s线路7—8中的一回线k处（仿真中k取距母线（7） 0.1分点）发生三相对称接地短路，故障中的对地电抗为0.000 1 pu，0.65 s故障切除，系统恢复到初始运行状态.机组G1采用逆汽门控制器，闭环控制器φ1采用PI控制，本例中取比例环节为30，微分环节为5，其余机组采用传统的控制器，仿真结果如图3所示.

由图3可见，系统的稳定速度大大加快，机组G1的功角振荡被很快平息，逆控制器取得了良好的控制效果.

5 结论

本文针对电力系统元件非线性DAE子系统模型，提出了一种新算法研究其逆系统控制问题.新算法避免了已有结果所需要的复杂变换，计算更为简单，具有更好的应用性.若被控元件可逆，则利用逆系统方法，通过状态反馈与动态补偿，设计出α阶积分右逆系统，将元件被控对象补偿成标准的积分型解耦系统，从而可以应用线性控制的理论和方法，使元件被控对象满足期望的性能指标.

参考文献

References

[1] Hill D J，Mareels I M Y.Stability theory for differential algebraic systems with application to power systems[J].IEEE Transactions on Circuits & Systems，1990，37（11）：1416-1423

[2] 王杰，陈陈.电力系统中微分代数模型的非线性控制[J].中国电机工程学报，2001，21（8）：15-18

WANG Jie，CHEN Chen.Nonlinear control of differential algebraic model in power systems[J].Proceedings of the CSEE，2001，21（8）：15-18

[3] 戴先中，张凯锋.复杂电力系统的接口概念与结构化模型[J].中国电机工程学报，2007，27（7）：7-12

DAI Xianzhong，ZHANG Kaifeng.Interface concept and structural model of complex power systems[J].Proceedings of the CSEE，2007，27（7）：7-12

[4] 戴先中，张凯锋，臧强.基于结构化模型的电力系统元件非线性分散控制方法[J].中国电机工程学报，2008，28（22）：15-22

DAI Xianzhong，ZHANG Kaifeng，ZANG Qiang.Nonlinear decentralized control method of power systems based on component structural model[J].Proceedings of the CSEE，2008，28（22）：15-22

[5] 臧强，张凯锋，戴先中.非线性微分-代数子系统的反步控制及应用[J].系统工程与电子技术，2013，35（8）：1736-1741

ZANG Qiang，ZHANG Kaifeng，DAI Xianzhong.Backstepping control of nonlinear differential algebraic equation sub-systems and its application[J].Systems Engineering and Electronics，2013，35（8）：1736-1741

[6] Rios A L，Messina A R.Order-reduction of nonlinear differential-algebraic equation models with application to power systems[J].Electric Power Components & Systems，2012，40（15）：1690-1707

[7] 吳热冰，李春文，刘艳红.非线性广义系统的右可逆性[J].自动化学报，2003，29（6）：927-931

WU Rebing，LI Chunwen，LIU Yanhong.Right invertibility of nonlinear singular systems[J].Acta Automatica Sinica，2003，29（6）：927-931

[8] 戴先中，臧强，张凯锋.非线性微分代数子系统的逆系统的构造[J].自动化学报，2009，35（8）：1094-1100

DAI Xianzhong，ZANG Qiang，ZHANG Kaifeng.Construction of inverse system for nonlinear differential-algebraic equations subsystems[J].Acta Automatica Sinica，2009，35（8）：1094-1100

[9] 臧强，戴先中，张凯锋.基于结构化模型的电力系统元件逆系统控制方法[J].东南大学学报（自然科学 版），2009，39（2）：299-303