抽样分布理论的模拟分析

潘传快 熊巍

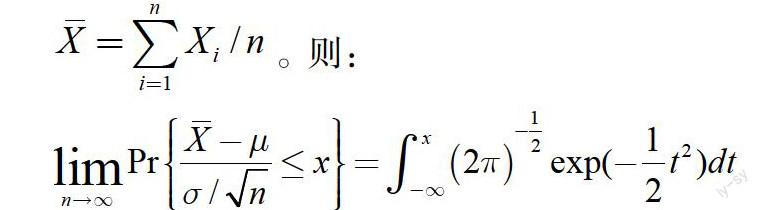
摘 要：抽样分布理论是统计学的核心理论，也是统计学教学的重点和难点。借助计算机进行统计模拟分析，可以形象生動地将该理论的核心思想展现给学生，使学生能更简单深入地理解该理论。

关键词：抽样分布；大数定律；中心极限定理；统计模拟

中图分类号：O17 文献标志码：A 文章编号：2096-000X（2017）08-0192-03

Abstract： Sampling distribution theory is the core theory of statistics， and it is also the key and difficult point in the teaching of statistics. Through carrying out statistical simulation analysis with the aid of the computer， the core idea of the theory can be vividly displayed to students， and they can understand the theory more easily and deeply.

Keywords： sampling distribution； law of large numbers； central limit theorem； statistical simulation

一、问题的提出

以均值为例，抽样分布理论主要是讨论样本均值的性质。这部分理论的主要内容有：样本均值的位置与尺度、样本均值和总体均值的关系以及样本均值的分布形态。主要涉及到两个定理：大数定律和中心极限定理。抽样分布理论是基础理论，区间估计理论和假设检验理论都建立在抽样分布理论的基础上，因此这部分内容极为重要。但是由于该理论涉及两个定理，这两个定理如果用文字表达比较简单，也容易理解但缺乏说服力，如果用数学推导则难度较大而且很抽象。

如果引入统计模拟方法，可以很好地解决这个问题。统计模拟需要借助计算机的庞大计算能力，但思路简单易懂。因为抽样分布理论主要讨论样本均值的性质，我们可以事先模拟一个庞大的总体，然后按照设定的规则大量地从总体中抽取样本，再观测样本的性质以及与总体均值的关系。由于是模拟，所以所有的总体参数是事先设定的，我们就可以很好地比较样本均值和总体均值。本文接下来的第二部分模拟样本均值的位置和尺度；第三部分对大数定律进行模拟；第四部分模拟样本均值的分布；第五部分进行总结。本文所使用的统计模拟软件为R语言。

二、位置和尺度模拟

（一）总体的模拟

模拟总体来自一个均值为100，标准差为10的正态（高斯）分布，即：X～N（100，10），让总体容量为100000000。容量太大，模拟结果无法一一展示，其直方图如图1。

很显然，该总体来自正态（高斯）分布。进一步，总体数据的描述统计量如表1）。

均值和标准差跟事先设定的100和10几乎无差异，偏度和峰度都接近0，几乎完全服从正态（高斯）分布。

（二）位置

在有放回的简单随机抽样下，可以得到一个独立同分布的样本，因此容易推导出样本均值的期望：

即所有的样本均值的期望值为总体均值。对于一个庞大的总体，其样本接近无数个，因此也就有接近无数个样本均值，我们一次抽样只得到其中的一个样本均值。我们可以借助计算机产生大量的样本，然后计算他们的均值，看是否跟总体均值接近。

先产生8个容量为100的样本，箱线图如图2。

发现8个样本中位数（跟均值差异不大）围绕着100变动，那是否其均值就等于？滋呢？我们把样本数扩大，为了反映随着样本数扩大X无限接近？滋的过程，我们分别模拟10个、100个、1000个、10000个、100000个样本的情况，然后分别计算均值如表2。

发现只需抽10次X的均值已经很接近？滋了，当然随着样本个数增加X的均值会更接近？滋，但当样本个数增加到10000以后，偏差改变就很小了。

（三）尺度

在有放回的简单随机抽样下，因此容易推导出样本均值的标准差（标准误）：

在模拟的情况下，总体标准差？滓事先已知，即可以实现算出：

这样就可以利用大量的样本来检验X的标准差。我们仍把样本数扩大，观察随着样本数扩大X的标准差无限接近S（X） 的过程，计算结果如表3。

发现抽取10个样本时，X的标准差跟理论值已经差别很小了，当样本数扩大到100000时，X的标准差和理论值已经几乎没有差异了。

三、大数定律的模拟

（一）大数定律

大数定律是指随着样本观测数的增加，均值和频率会不断稳定，在抽样分布理论中主要指切比雪夫定理。对于任意？着>0，有：

这个定理证明有点复杂，但意思却很简单，即随着样本容量的无限增加，样本均值无限接近总体均值。

（二）模拟

下面我们模拟随着样本容量增加，样本均值接近总体均值的过程。让样本容量逐次取10、100、1000、10000、100000、1000000，获取样本计算均值，表4记录了它们的结果。

我们发现，样本容量为10的时候样本均值和总体均值（100）的差距还是较大的，但随着样本容量增加差距变小，当样本容量为1000000时，这个差距已经小到可以忽略。为了更形象地说明样本均值随着容量的增加无限渐进总体均值的过程，我们把实验次数增加到10000次（k=1，2，…10000），让样本容量为：

k+100×k

根据这10000个样本计算的均值按照先后顺序绘制的线图如图3。

图3很形象地描绘除了样本容量不断增加，样本均值无限接近總体均值的过程。

四、中心极限定理的模拟

（一）中心极限定理

中心极限定理主要是证明了样本均值的分布形态。中心极限定理有几个表达，我们列出最常用的一个。设随机变量X1，X2，…，Xn 独：立同分布（分布形态不限），其均值为：

这个定理看起来复杂也不容易证明，但意思很简单。那就是无论总体成何种分布，在样本容量足够大以后，样本均值服从以？滋为均值，？滓/■为标准差的正态分布。

（二）正态总体时的模拟

我们先模拟当总体是正态时的情形，为了清晰地看出中心极限定理，把样本容量从5慢慢增加到10、20，然后再增加到100、1000，然后在每个容量下抽取300个样本计算均值，绘出直方图如图4所示。

从图4中发现，在正态总体下，哪怕样本容量为5，样本均值的分布也接近正态，当然随着样本容量增大样本均值越来越接近正态分布，而且抽样误差也越来越小。

（三）指数总体时的模拟

直观的理解我们也会相信在正态总体下中心极限定理是显而易见的，但是在其它非正态的总体下，中心极限定理是不是也成立呢？我们模拟总体来自一个均值和标准差为100的指数总体，即X～EXP（0.01）。

仍然将样本容量从5慢慢增加到10、20、100、1000，然后在每个容量下抽取300个样本计算均值，绘出直方图如图5所示。

由于指数分布是个右偏的反J型曲线，因此其样本均值的分布也会受总体分布影响，呈右偏，这在样本容量小的时候尤为明显。图5中我们发现，当样本容量为5时，样本均值分布极为明显，但随着容量增加偏度下降，容量为1000时已经看不到偏态了，足以证明中心极限定理跟总体分布无关，只要样本容量足够大样本均值都会趋于正态分布。

五、结束语

鉴于计算机的强大计算能力，将模拟技术用于统计研究有极高的价值。在统计教学种应用模拟技术也有很好的效果，譬如用模拟来介绍抽样分布理论。在模拟的情况下，所有理论的假设条件都可以满足，而且事先知道总体，因此可以轻松而又深入地理解抽样分布理论，如大数定律、中心极限定理，而不用拘谨于繁杂的数学证明。

但是也需要指出，统计模拟都是随机的，因此每次模拟的结果不同，效果不同，在教学中需要注意到这个问题。本文利用R语言，将结果用设定的随机数种子固定，但是不同的实验，结果将不一样。

参考文献

[1]肖枝洪，朱强.统计模拟及其R实现[M].武汉：武汉大学出版社，2010.

[2]Sheldon M.Ross. 统计模拟[M].北京：人民邮电出版社，2007.

[3]Mills J D. Using computer simulation methods to teach statistics：A review of the literature[J].Journal of Statistics Education，2002，10（1）：1-20.

[4]Rubinstein R Y， Kroese D P. Simulation and the Monte Carlo method[M].John Wiley & Sons，2011.