曲线压缩斜率差限值法的设计与实现

陈杨 师芸

摘 要：本文对传统的偏角法进行分析，并指出其不足之处，针对不足然后提出斜率差限值法，然后通过两种实验结果来说明该算法的性优越性和可靠性。

关键词：曲线压缩；偏角法；斜率差限值法

线是地理要素之一，往往表示一些地物地貌，比如道路，地势高低等。通常，我们用曲线来表达实际的地物地形信息多一点。当代社会获取的数据手段越来越丰富，技术越来越先进。在面对大量的数据时，我们如何将采集来的数据进行合理的舍去，从而能保留必要的目标信息。目前具有代表性的压缩方法，有角度限值法等，但各自也存在不足，针对偏角法不足之处[ 1 ]，本文提出斜率差限值法来更好的应用于曲线数据的压缩。

一、偏角法

偏角法是从待处理的曲线的一端开始，选取相邻的三个点，第一点与第二点连线，同时第一点与第三点连线，计算此两线之间的夹角，若所得角大于限值则保留，否则剔除。后面的点按次法依次操作，直至所有点处理结束[ 1 ]。该方法对角度变化比较敏感，适用于平缓的曲线，但通过线段长度来换算夹角，这会增加计算量，导致耗时比较大，可能会舍去不该舍去点。如图1所示，P2点的偏角小于限差，应舍弃；P3点的偏角大于限差，应保留[ 2 ]。

二、斜率差限值法

该方法来源于直线的斜率思想。其基本过程如下：

1）首先确定一条曲线的始点，遐想有这样一个坐标轴，它的水平轴平行于过计算机屏幕左右底下角的连线，纵轴垂直于两底角的连线。

2）假设以始点P1向末点Pn作为前进方向，为了不失实际效果，始末点保留。每两点为一组，计算这两点的纵坐标变量Δy与横坐标变量Δx的比值作为斜率K，即K=。这里P1与P2为第一组，P2与P3为第二组，P3与P4为第三组，依次分下去，共计N-1个组。

3）判断点P2舍弃情况，用第二组的斜率与第一组的斜率两者差的绝对值ΔK与限差D比较，若ΔK依次类推，直至所有的点检测结束。简化示意图如图2所示。

三、实验分析

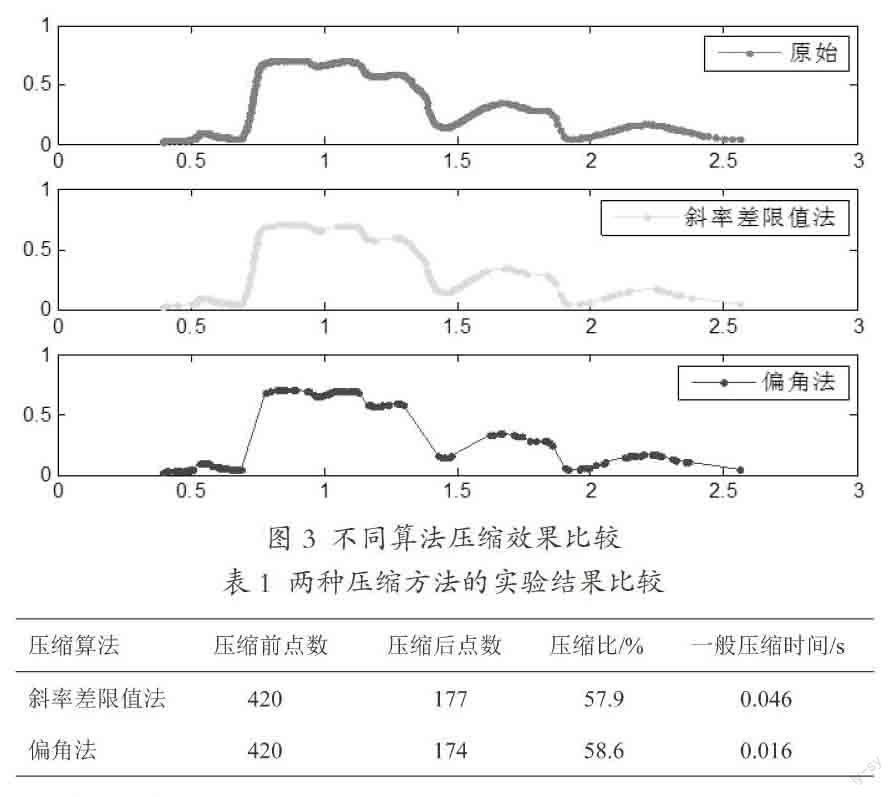
为了实现上述算法的可靠性，笔者用VC++6.0实现斜率差值限值法的算法[ 3 ]。并借助MATLAB绘制压缩图。实验數据来源于www.wei2008.com网站。压缩时，斜率差限值法阙值设置为0.5，偏角法限差设置为5.5。实验效果如图3所示。两种方法压缩属性如表1所示。

从图3与表1可以看出用偏角法压缩后，在某些地方发生形变，而利用斜率差限值法，压缩后仍然接近原来的形状。在压缩比大致一样时，斜率差限值法压缩的时间要比偏角法要少些。

四、结语

通过实验比较，本文论述的斜率差限值法比偏角法更具有优势。偏角法只是单纯的从角度出发，没有考虑直线的方向性；而斜率差限值法不仅考虑了角度，也考虑了直线的方向性；在计算时，只计算两点的横坐标变化量和纵坐标变化量及比值，避免了求线段长度，从而减少压缩时间。为矢量数据压缩带来一定的技术支撑，具有一定的实用价值。

参考文献：

[1] 赵永清.自动设置阙值的道格拉斯-普克压缩法[J].山西煤炭管理干部学院学报，2013，26（3）：120-122.

[2] 汤国安，刘学军，等.地理信息系统教程[M].北京：高等教育出版社，2007.

[3] 张胜，朱才连，钟世明.Douglas-Peucker 算法的改进及应用[J].武汉理工大学学报，2005，29（5）：671-674.