Hydrodynamic dispersion ofreactive solute in a Hagen-Poiseuille flow of a layered liquid

Sudip Debnath *,Apu Kumar Saha B.S.Mazumder ,Ashis Kumar Roy

1 Department of Mathematics,National Institute of Technology,Agartala 799046,India

2 Fluvial Mechanics Laboratory,Physics and Applied Mathematics Unit,Indian Statistical Institute,Kolkata 700108,India

3 Fluid Mechanics and Hydraulic Laboratory(FMHL),DepartmentofAerospace Engineering and Applied Mechanics,Indian Institute ofEngineering Science and Technology(IIEST),Shibpur,Howrah 711 103,India

1.Introduction

Dispersion is the process which is utilized as an efficient means to accomplish the dilution or mixing.In recent days,the study on the longitudinal dispersion has gained attention due to its practical importance in the field of chemical engineering,physiological fluid dynamics,environmental sciences,biomedical engineeringetc.for both corporeal and extra-corporeal.Specifically nutrients,metabolic items,drugs,etc.get transported through blood flow,as a consequence of diffusive and convective mechanisms.The pioneer researcher in this field was Taylor[1,2]and a vital resulting commitment was tailored by Aris[3],who framed and partially solved equations for the integral moments of the cloud of contaminant.Sankarasubramanian and Gill[4]developed a derivative expansion methodviz.‘generalized dispersion model’,which holds true for large as well as small times.A numerical study was performed by Ananthakrishnanetal.[5]to solve the convective diffusion equation by a standard finite difference method which went on to show that the Taylor-Aris dispersion theory was pertinent only for adequately expansive estimation of the dimensionless time,i.e.,t＞0.8.Barton[6]re fined Aris's model and extended the legitimacy to cover even small and moderate times.

Following different techniques,a large number of articles[7-12]have been found in literature dealing with longitudinal dispersion in steady and unsteady flows within the Newtonian and non-Newtonian fluids(pipe/channels)with or without chemical reactions.Aris[13]first examined the longitudinal dispersion in an in finite tube by considering the periodic pressure gradient as the driving force.A solution for the problem of transient multicomponent dispersion in fully developed laminar flow was determined by Harry[14].The unsteady convective diffusion with a heterogeneous chemical reaction in a plane-Poiseuille flow of micropolar fluid was studied by Siddheshwar and Manjunath[15].Using asymptotic analysis with respect to the pipe thickness,the transport of reactive solute by diffusion and convection in a thin(or long)curved and circular pipe was considered by Pažanin[16,17].For making a rise in solute diffusion,Duijnet al.[18]proposed a model of the reactive flow through a pore,under dominant Peclet and Damkohler numbers.Paul[19],and Bandyopadhyay and Mazumder[20]studied the effect of unsteady flow in solute dispersion considering the movement of the boundary wall.Using the method of moments Bandyopadhyay and Mazumder[21]studied the effect of pulsatile flow on the dispersion process in a channel,also Sarkar and Jayaraman[22],Mazumder and Mondal[23]investigated the effect of wall absorption on dispersion in oscillatory flow in an annulus and explained the application of their study to a catheterized artery.

In modern days,dispersion in non-Newtonian fluids is being widely used in the field of bio-chemical processing,cardiovascular system,polymer processingetc.In 1993,Sharp[24]studied the dispersion phenomena in non-Newtonians fluids(Casson,Bingham plastic and power law fluids)through conduits using the Taylor-Aris dispersion model.A brief review on the dispersion in power law fluids was done by Agrawal and Jayaraman[25].Using the generalized dispersion model of Sankarasubramanian and Gill[4],shearaugmented unsteady dispersion of a solute in Casson fluid flowing through a conduit was analyzed by Dashet al.[26].The study revealed that in blood flow the yield stress considerably affects dispersion rate of fluid.The in fluence of interphase mass transfer on solute dispersion in a channel and tube flow of powerlaw fluid are inspected by Siddheshwaret al.[27,28]after the injection of the solute.Lately,Nagaraniet al.[29]discussed the longitudinal dispersion and its application in catheterized artery assuming the Casson fluid through an annulus.

In some of the above investigations,the effectiveness of longitudinal dispersion in blood flow was discussed where blood has been treated as Newtonian and non-Newtonian liquid relying upon the estimation of shear rates.The suspicion of Newtonian behavior of blood is adequate for high shear rate flow through larger arteries[30].Yet,blood,being a suspension of cells in plasma,exhibits non-Newtonian behavior at low shear rate＜10s-1in small diameter arteries(0.02-0.1 mm)[31].Different experiments were performed on blood(Scott Blair[32],Charm and Kurland[33])with the assortment of hematocrits,anticoagulants,temperature and so on suggested that the behavior of blood at low shear rate can be described sufficiently by the Casson model.In particular,when blood flows through small blood vessels,the presence of a peripheral layer of plasma(Newtonian liquid)and a core region of suspension of all the erythrocytes as a non-Newtonian liquid has been found,which was experimentally appeared by Bugliarello and Sevilla[34]and Cokelet[35].Thus,for a practical portrayal ofthe blood stream,itis more appropriate to regard blood as a two-liquid(or three-layerliquid)model comprising all the erythrocytes thought to be Casson liquid and a peripheral layer of plasma as Newtonian liquid.There are several worksavailable in the literature revealing the significance ofthe peripherallayer in the functioning ofthe flowcharacteristics ofthe arterialsystem.Srivastava and Saxena[36]showed that the resistance to flow increases as yield stress increases and also the magnitudes of the flow resistance found to be decreasing with the increase in the expansion of the peripheral layer.In a two- fluid,blood flow analysis,Sankar[37,38]observed that the velocity distribution and flow rate decrease but the wall shear stress,width of the plug flow region and longitudinalimpedance increase when the yield stress increases.We have seen very few works of dispersion considering peripheral layer effects,such as Shukla and Parihar[39],and Shukla and Gupta[40].To the best of our knowledge,there is hardly any work in the literature considering the effect of the peripheral layer on dispersion process,when the core region is Casson liquid and a peripheral layer of plasma is Newtonian liquid.Moreover,the present study manages the irreversible absorption at the boundary of the pipe.Due to the fact of peripheral layer presence,the viscosity ratio appears forthe firsttime in the study ofhydrodynamic dispersion.The present model may be useful for the physiological blood flow analysis as the nature of the effects considered in the study,the work is much closer to that in a physiological situation compared to several other works in literature.

2.Mathematical Formulation

A uni-directional,steady laminar,axi-symmetric,fully-developed flow of an incompressible,three-layer liquid through a circular pipe of radiusRis considered.Itis assumed that the core region is Casson liquid enclosed by a thin layer of Newtonian liquid.

Fig.1 shows the flow geometry with a cylindrical coordinate system where the axialand radialcoordinates are represented by ¯zand ¯rrespectively(the bar denotes dimensional quantities).On account of enough axial covering of the tube and for the low Reynolds number flow,it can be shown that the radial velocity is negligibly small and can be disregarded,thus the fully developed flow is only in the axial direction.Because of the axi-symmetry all quantities are independent of θ.

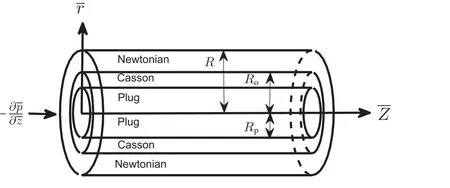
Fig.1.Schematic diagram of the setup under consideration.

The governing equations of motion for the axial flow are given by

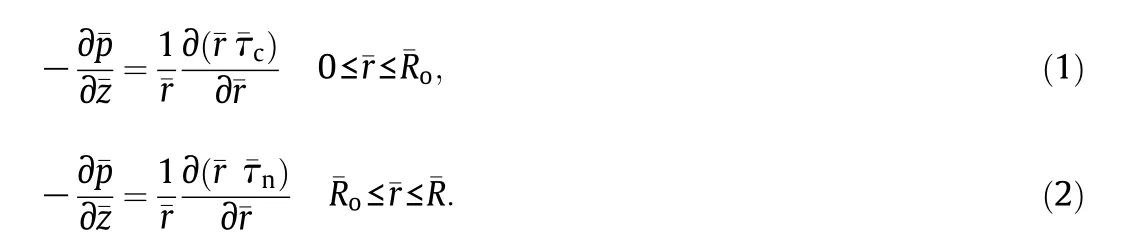
Let us now consider the transport and spreading of chemical species with the solvent flowing through the tube which is supposed to be completely miscible with the liquid.The species are alleged to contain irreversible absorption into the wall.

In the present scenario,the transport equation that governs¯C（¯t,¯r,¯z）is the unsteady convective diffusion equation and is given by

Using the following dimensionless quantities:

along with initial and boundary conditions as:

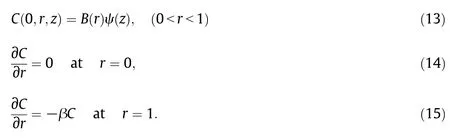
With the assistance of above boundary conditions(4)in dimensionless form,the velocity distributions are acquired as:

(1)Aris-Barton approach and

(2)Sankarasubramanian-Gill approach.The two approaches are described in necessary detail in the next two sections.

3.Aris-Barton Approach

Thepth moment of the distribution of the solute in the direction of flow can be described by Aris-Barton[6]as,

The cross-sectional average of thepth moment of the distribution of solute is given by:

represents the ‘centroid’or ‘ first moment’of the distribution of solute and 〈C(0)〉is the totalmass ofthe chemicalspecies in the flowing stream.

The expressions forcentralmoments can be obtained from Eq.(23)as,

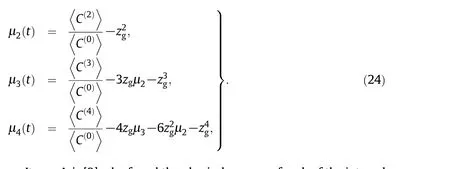
It was Aris[3]who found the physical essence of each of the integral moments of concentration de fined by Eq.(24)while explaining the dispersion phenomena on liquid.For instance,the zeroth moment gives the aggregate range under the distribution curve which corresponds to the total mass of the solute,the first moment measures the location of the center of gravity of the slug moving with the mean velocity of the liquid and second centralmomentrepresentsthe variance ofthe distribution about the mean position whose rate of change gives the dispersion coefficient.

The reaction coefficientorexchange coefficientM0can be figured from the way that the total mass decays exponentially with time according to:

Following Aris[3]the apparent dispersion coefficient,Da,can be expressed as follows:

4.Sankarasubramanian-Gill Approach

Following the model developed by Sankarasubramanian and Gill[4],the concentration expands as

In lightof the non-zero solute flux at the outer boundary of the wall,M0(t)arises,which corresponds to the absorption parameter.As the solute undergoes an irreversible reaction at the outer boundary,it will deplete with the time that makes negative exchange coefficient.In such a case exchange coefficient would be positive as β in Eq.(15)would take on a negative sign.M1(t)andM2(t)relate to the convective and dispersion coefficients respectively.It is necessary to mention thatM2(t)is analogous to the dispersion coefficient(Da)obtained from the Aris-Barton method of moments.

5.Finite Difference ofthe Unsteady Convective Diffusion Equation in the Three-layer Region to Obtain Transport Coefficients

Due to the presence of complexity in the analytical solution,in this section,we have numerically computed the solution of the moment Eq.(18)with initial and boundary conditions(19).For all time periods,when the solute is injected uniformly over the cross-section of the pipe,we developed a finite difference formula in view of the Crank-Nicolson implicit scheme,where the entire width of the pipe has been divided into(M-1)equal parts having length Δr.The lengths and times are represented by the grid pointjandirespectively,so thatthe generalformulas arerj=(j-1)×Δrandti=Δt×(i-1).In this way,forj=1,Mcorresponds to the axis of the pipe(r=0)and the wall(r=1)of the pipe respectively,also asi=1 corresponds to the initial time(t=0),where Δtand Δrare the augmentations oftandrrespectively.C(p)(i,j)indicates the value ofC(p)at thei-th grid point along thet-axis andjth grid point alongr-axis.The resulting finite difference formula leads to a system of algebraic equation with a tri-diagonal coefficient matrix,

A MATLAB code has been developed to solve the tri-diagonal coefficient matrix rendered from Eq.(39)by the method of the Thomas algorithm(Andersonet al.[41])with the help of prescribed initial and boundary conditions.The computation steps are:

Step-1:The time independentaxialvelocityuis computed firstfrom Eq.(16).

Step-2:The concentrationC(p)is then calculated from Eq.(18)as the value ofu(r)at each of the grid points is known fromStep-1.

Step-3:Finally the value of 〈C(p)〉is calculated from Eq.(20)by applying Simpson's one-third rule,using the values found from

Step-1andStep-2at the corresponding grid points.

Having numerically obtained the transportcoefficients from the above two all-time approaches,we now outline the procedure of obtaining the mean solute concentration distribution in the layered liquid medium.

6.Calculation ofthe Non-Gaussian Mean Solute Concentration Using Hermite Polynomials

The behavior of concentration distribution might also be acquired from the information of the first four central moments of the distribution.Utilizing these four moments,it is possible to approximate the mean axial concentration distributionCm(z,t)of tracers within the flow region with the assistance of Hermite polynomial representation for non-Gaussian curves(Mehtaet al.[42])and is given by,

Therefore,given the statisticalparameters in Eq.(24),the concentration distribution can be estimated from Eq.(40)at any given location in the axial direction and time.

7.Results and Discussion

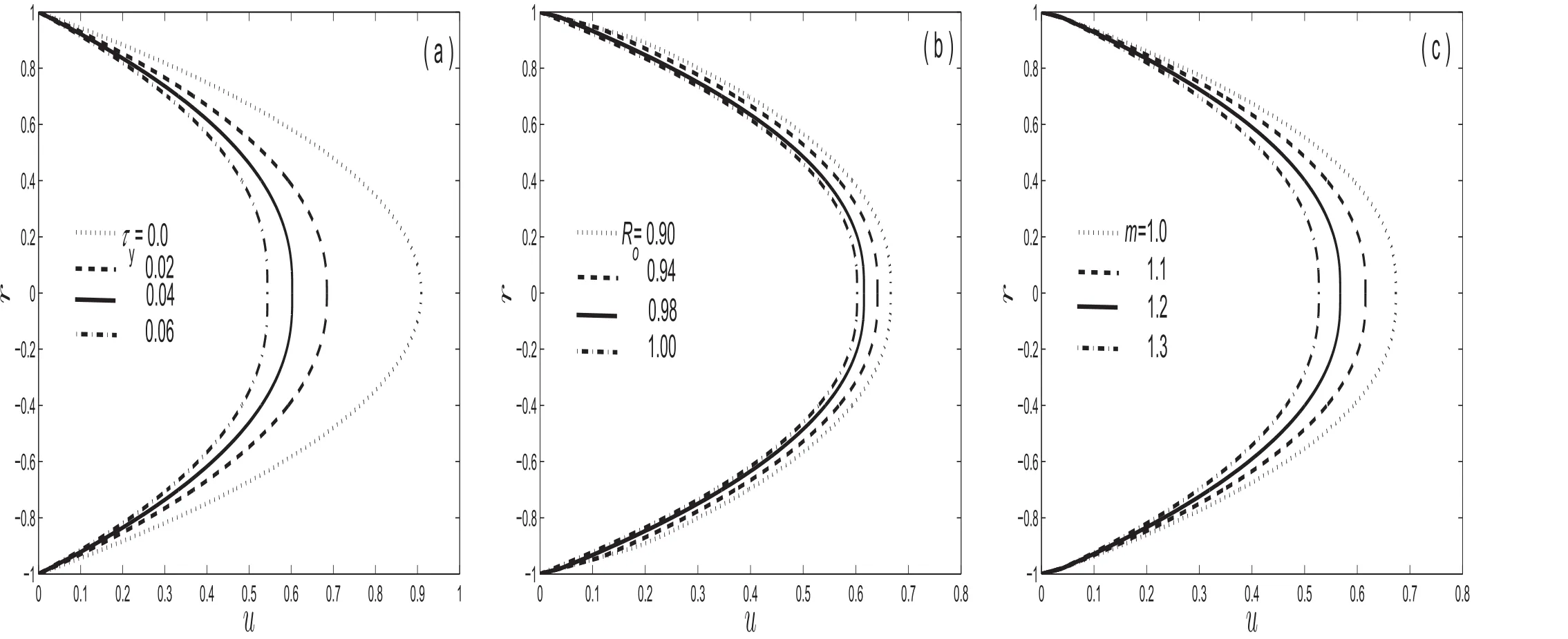
The present analysis essentially deals with the stream-wise dispersion of solute in solvent flowing through a narrow pipe under the effect of peripheral layer thickness with irreversible reaction occur at the boundary.In line with the discussions outlaid in Section 1,the importance of the effect of peripheral layer in blood flow,the values of yield stress and peripheral layer thickness assume a pivotal significance.As indicated by McDonald[43],blood possesses a yield stress of 0.04 dyn·cm-2at a hematocrit value of 40%.In contrast to published studies in this direction,the present study has investigated the parametric effect of molecular diffusivity at different liquid layers which has helped to project the importance of viscosity ratio in the present paradigm of study.In order to establish the desired parametric effect both qualitatively and quantitatively,variables were investigated in the following ranges:(1)irreversible absorption parameter(β)from 0 to 100,(2)yield stress(τy)from 0 to 0.2,(3)viscosity ratio(m)ranges from 1 to 1.2 and(4)peripheral layer variation(Ro)varies from 0.86 to 1.Fig.2 demonstrates the velocity profiles with respectto the pipe radius at different parametric values of τy,Roandm.

To verify the accuracy of the numerical scheme,the following cases have been considered:

(1)In order to compare the results of dispersion obtained in the present study with that established in the study of Sankarasubramanian and Gill[4]the parameters of interphase mass transfer under constant pressure gradient have been characterized with the same values ofRo=1,Dp=Dc=1,m=1 andRp=0.0,(for Newtonian fluid).The present model has been further investigated with varyingRp=0.02,0.04,0.06,0.08,0.1,0.2 which corresponds to the dispersion studies ofNagaraniet al.[44]for comparison of the model viability in the case of Casson fluid.Fig.3 represents the plot of dispersion coefficient(M2)vs.absorption(β).As is evident from the results obtained,the model trends completely concur qualitatively with that obtained in the studies of Sankarasubramanian and Gill[4]and with Nagaraniet al.[44].However the quantitative differences realized in the present study are attributed to differing normalization scales adopted in the present study.

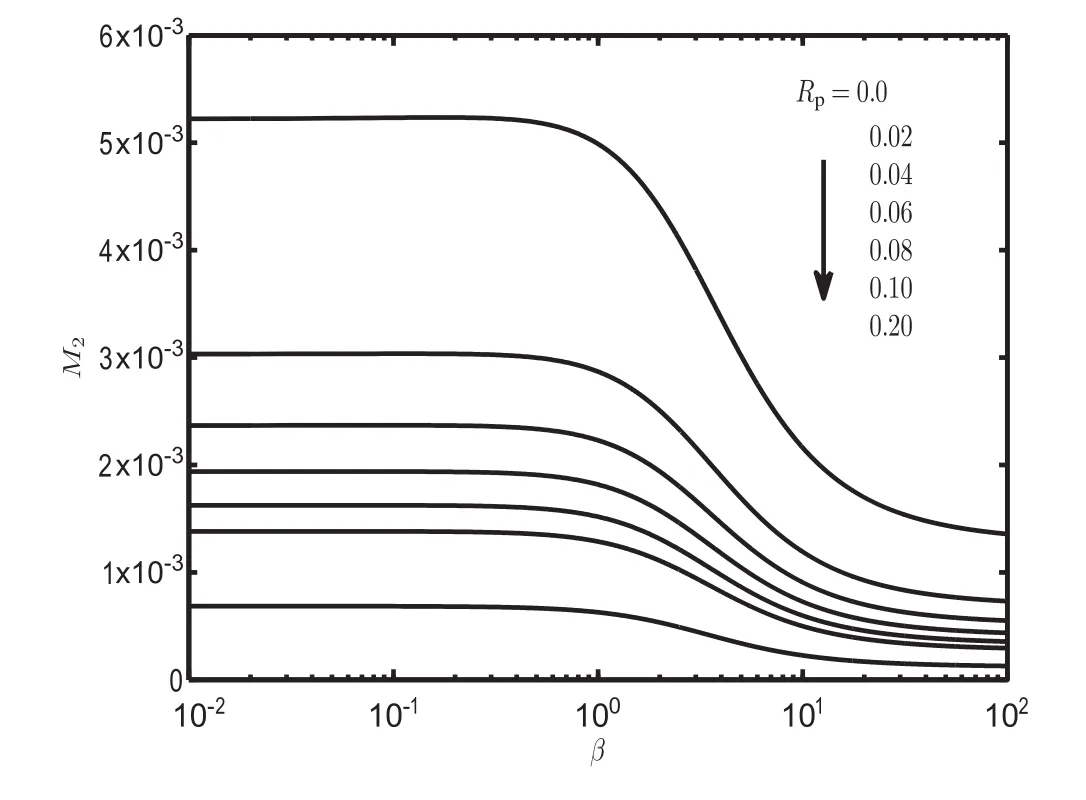
Fig.3.Variation of dispersion coefficient(M2)with absorption parameter(β)for various values of plug radius(R p)for the case when R o=1,m=1 and D p=D c=1.

(2)In order to validate the present model response with those established in the study of Dashet al.[26],the simulation parameters ofRo,Dp,Dcandmbearing their individual significance had been kept at unity.To this end,the model responses outlaid in Fig.4 display complete agreement with those obtained in the study of solute dispersion of Dashet al.[26]without catalytic wall reaction,i.e.β=0(see Fig.4 totally coincides with Fig.2(a)in[26]).

In order to validate the robustness of the present models,the convection diffusion mechanism paradigm was addressed,both through the method ofmoment[6]as wellas with thatofthe generalized dispersion model[4].Simulation response to this effecthas been encapsulated in Fig.5.The value of the dispersion coefficient(Da)obtained from the‘method of moment’and the dispersion coefficient(M2)acquired from the ‘generalized dispersion model’for both Newtonian and Casson liquid case studies under the same parametric environment,yields striking quantitative and qualitative resemblances independent of the models so chosen to this end.

For the rest of our analysis,effects of different parameters on transport coefficients have been examined by Aris's method of moments.

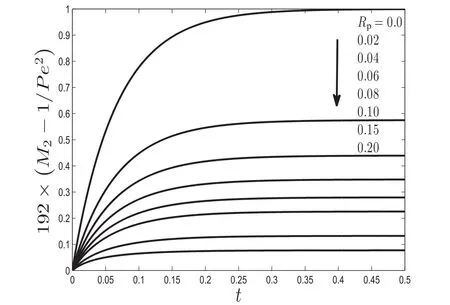
Fig.4.Variation of dispersion coefficient[192×(M2-1/Pe2)]with time(t)for various values of plug radius(R p)for the case when R o=1,m=1,D p=D c=1 and β=0.

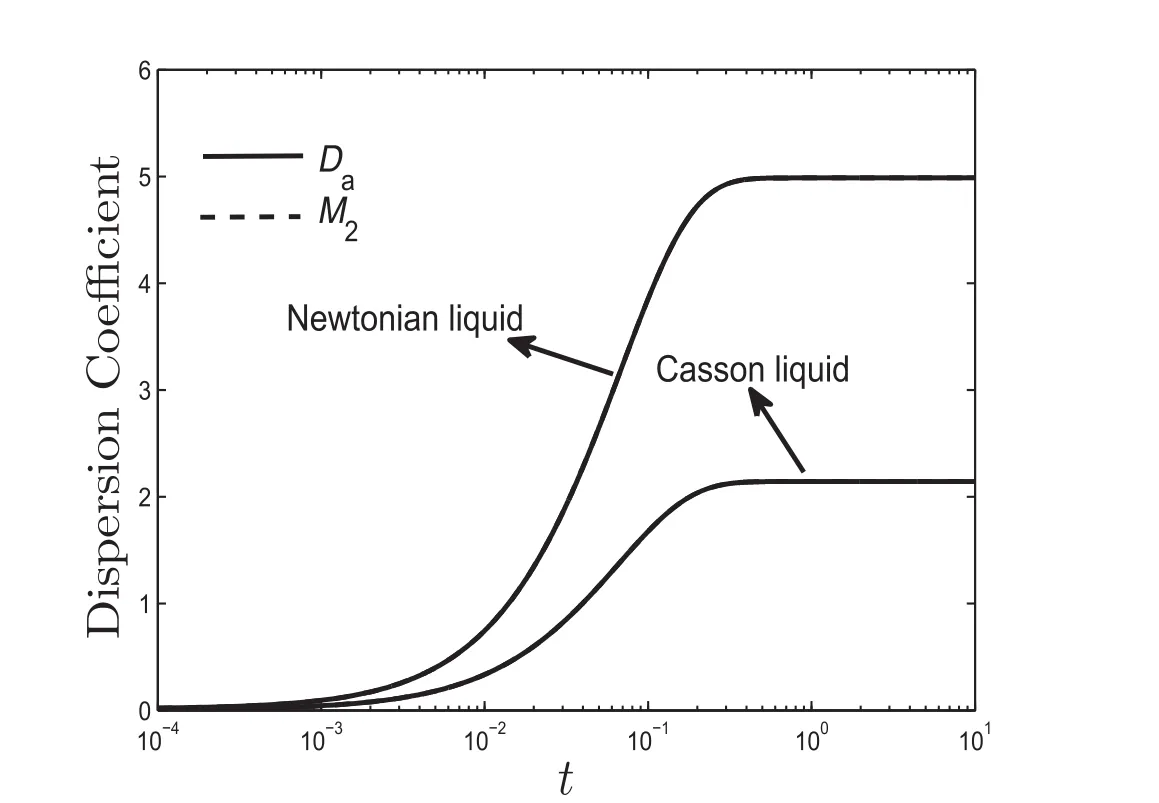
Fig.5.Variation of dispersion coefficient with time obtained by moment method(solid line)and generalized dispersion model(dashed line).The chosen parameter values are:m=1,D p=D c=1.For the case of Newtonian liquid,τy=0,R o=1 and for Casson liquid,τy=0.04,R o=1.

7.1.Exchange coef ficient

The variation of exchange coefficient(M0(t))with time has been interpreted through Fig.6 under the impact of reaction parameters(β),yield stress(τy)and viscosity ratio(m).

Fig.6(a)clearly shows thatthe increase inβmakes an augmentation ofM0.The increase inM0with β can be attributed to the expanding loss of solute at the wall as β increases.It is to be noted here thatM0exists due to the presence of chemical reaction which is independent of τyandmas seen in Fig.6(b,c).Eq.(31a)further elucidates thatthe peripheral layer effect onM0does not vary the outcomes acquired for purely Casson liquid flow.

7.2.Convection and dispersion coef ficients

For purely Casson and peripheral layer liquid flows,variations of the convective coefficient(M1(t))and apparent dispersion coefficient(Da(t))with respect to time(t)are shown in Fig.7 for various estimations of the reaction parameter(β),yield stress(τy)and viscosity ratio(m).The lines with asterisk have been shown in figures due to Casson liquid flow,whereas the rest are due to peripheral layer liquid.A wide range of time is considered to track the asymptotic approach of the dispersion coefficient.

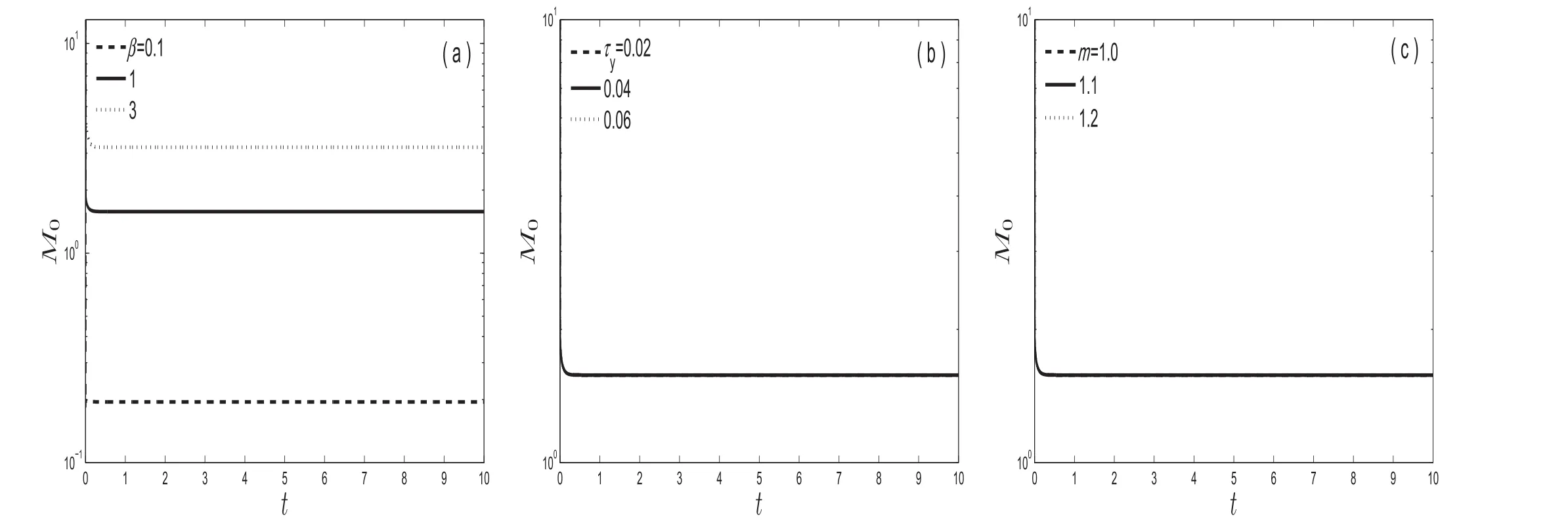
Fig.6.Time assessment of exchange coefficients(M0)in a purely Casson liquid flow for the fixed R o=D p=D c=1,(a)variation of absorption parameter(β)when m=1.1 and τy=0.04;(b)variation of yield stress(τy)when m=1.1 and β=1;(c)variation of viscosity ratio(m)when τy=0.04 and β=1.

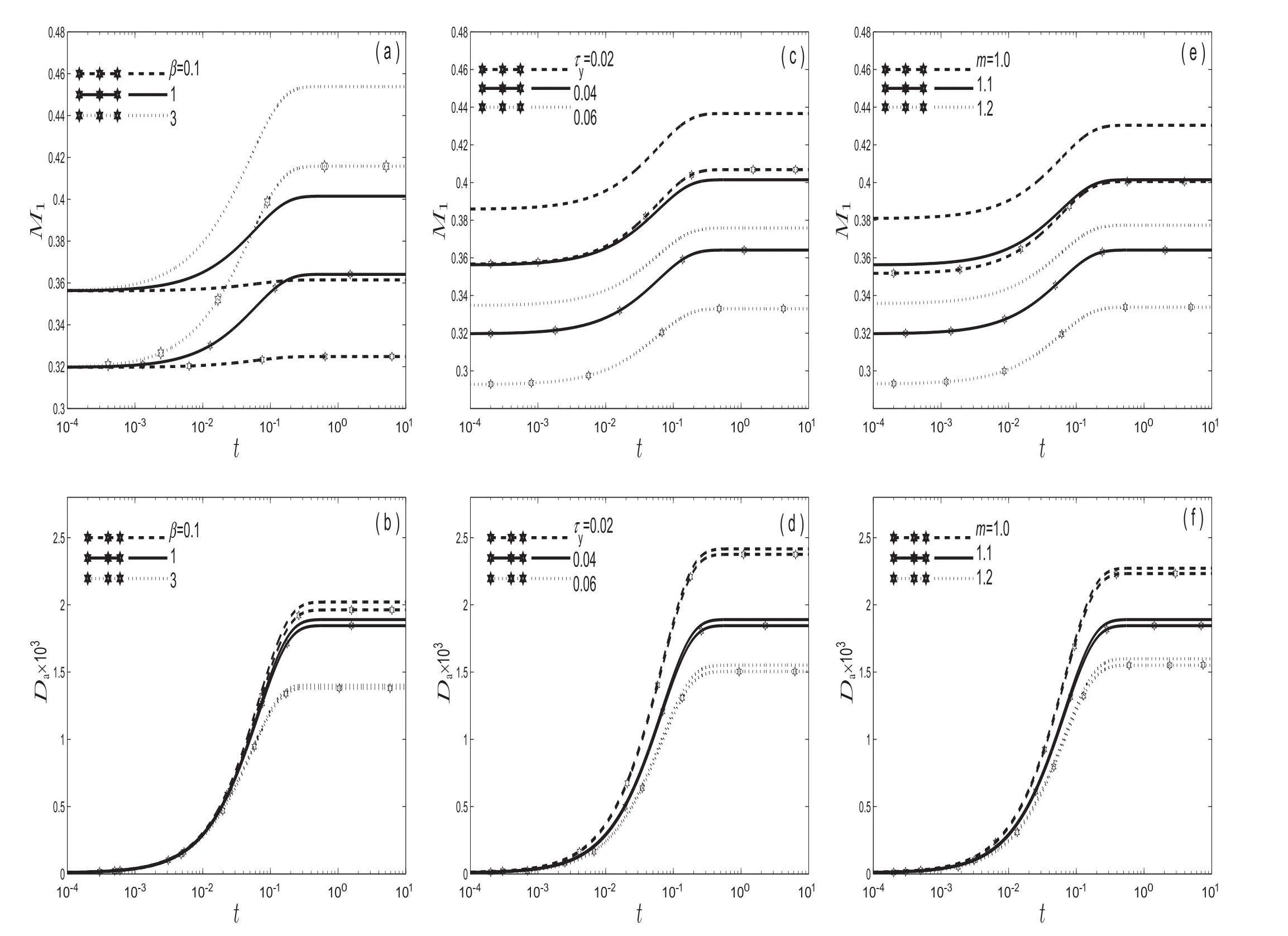
Fig.7.Time assessmentoftransportcoefficients(M1 and D a)in purely Casson liquid flow(asterisk lines)forthe fixed R o=D p=D c=1,and in three-layerliquid flowforthe fixed R o=0.94 and D p=D c=1,(a-b)variation of absorption parameter(β)when m=1.1 and τy=0.04;(c-d)variation of yield stress(τy)when m=1.1 and β=1;(e-f)variation of viscosity ratio(m)when τy=0.04 and β=1.

Profiles in Fig.7(a,b)represent the behavior ofM1andDafor same values of β variation.From Fig.7(a,b),it is observed thatM1increases whileDadecreases monotonically with β until it reaches their respective steady state values.Since the wall reaction enhances the transport of solute towards the wall,subsequentlyM1increases with β.From Fig.7(a),it can be said thatM1reaches earlier to its asymptotic value with the decrease in β,since weak absorption makes an equilibrium between the diffusion of solute and the wall reaction occurs within small time frame.In Fig.7(b),the physical perception about the decrement ofDawith increasing β leads to an increase in the quantity of moles of reactive material undergoing chemical reaction or absorption resulting in a change in the concentration distribution across the tube with the simultaneous consequence of a drop in dispersion coefficient.The present study yields a unique observation as evident in Fig.7(a,b)is that the presence of a peripheral layer makes larger values inM1andDaas compared to single Casson layer liquid flow.This trend is also evident from subsequent Fig.9.

Fig.7(c,d)has been drawn to emphasize the effect of τyonM1andDain order to highlight the pivotal significance of low shear rate applicable to blood flow through small blood vessels in the presence of the peripheral layer.While observing Fig.7(c,d),it is clearly evident thatM1andDadecreases with increasingτy.This is attributed to the fact that the increase in τy(or in other words,an increase in the non-Newtonian parameter)decreases the velocity of the fluid.The importance of a peripheral layer can be appreciated from the observation of the increased value ofthe coefficients as compared to Casson liquid alone.The reason behind these increments is due to Newtonian layer effect,which has lesser viscosity than non-Newtonian Casson liquid.

Viscosity ratio(m)is de fined as the ratio between Casson viscosity(μc)and Newtonian viscosity(μn).In the present study,the appearance of viscosity ratio(m)is due to the peripheral layer.The main advantage of usingmon the study of dispersion is that it directly discloses as to how strong the in fluence of μcis compared to μn.The time evaluation of convection coefficient(M1)and dispersion coefficient(Da)under the effect ofmhas been projected in Fig.7(e,f).As can be inferred from Fig.7(e,f),we can observe thatM1andDaincrease with time(t)for a short period beyond which they attain a steady state trend.Again,asmincreases the magnitudes ofM1andDadecrease.This happens in light of the fact that the increment ofmcauses a decrease in velocity distribution(see Fig.2(c)).For Casson liquid flow,whenm=1.1 andt=0 the increments inM1andDaare 1.13 and 198.7 times the value corresponding tot=10,butfora three-layerliquid thisincrement is 1.15 and 200 times respectively.While comparing the Casson liquid and the corresponding three-layer liquid stream,it is observed that,bothM1andDaincrease more in the case of the three-layer liquid stream as compared to that in the Casson liquid environment.From the investigation,in Fig.7(e,f),it can be calculated that for the time interval[0,10]and viscosity ratio(m=1.1),the value ofM1increases in the range(0.0365-0.0374)whereas the value ofDaincreases in the range(1.49×e-6-4.5×e-5).

7.3.Mean concentration pro file

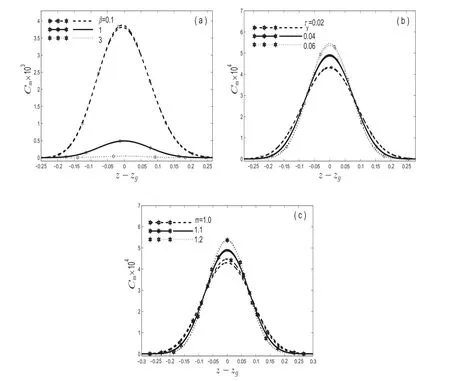
Fig.8 presents the study of mean concentration distribution across axial distance for steady nature of stream at a fixed timet=1.5.Fig.8(a)deals about the effect of absorption parameter(β)on mean concentration distribution whereas Fig.8(b)and(c)measures the in fluence due to τyandmrespectively.Due to constant depletion occurring at the tube wall in both the cases,the peak of the mean concentration decreases as β increases.It may become flat for large absorption,thus the dispersion coefficient may not have practical importance for large β.While observing Fig.8(b,c),it is found that as τyandmincrease,the peak of the mean concentration distribution also increases.From Fig.8(a,b,c),it can be clearly observed that peripheral layer presence makes faster decrements in peak length as compared to purely Casson liquid flow.

7.4.Effect of peripheral layer on transport coef ficients

To observe the effectof peripheral layer variation on the three transport coefficients as well as on mean concentration distribution,a discernible impact has been observed through Figs.9 and 10.The exchange coefficient(M0)is independent ofRo,which has been shown in Fig.9(a)and it completely agrees on the physics of the present model.Fig.9(b,c)depicts that the convection coefficient(M1)and dispersion coefficient(Da)both decrease as the value ofRoincreases(or peripheral layer thickness decreases).The physical explanation about such kind of behavior is that the larger value ofRomakes the smaller region for Newtonian liquid,hence the velocity of the liquid decreases resulting in the smaller convection and diffusion rate.Fig.10 clearly indicates that peak of the mean concentration distribution increases asRoincreases.This is due to slow tracer spreading over the entire region.

7.5.Effect of molecular diffusivity on dispersion coef ficient

The molecular diffusivity or diffusion coefficient(D)is a kinematic property of the fluid which implies that the mass of the substance diffuses through a unit surface in a unit time at a concentration gradient of unity.So,diffusion coefficient(D)represents the spreading process,the larger value ofDindicates the rapid spreading of the tracer curve whereas smallerDimplies slow spreading of solute in the liquid.Fig.11 shows the effect ofDon the apparentdispersion coefficient(Da).

Fig.11(a-c)clearly shows that larger values in diffusivity belonging from the regionRcor plug regionRp,cause decreases in dispersion coefficient coefficient decreases.The reason for this decrement is due to the fast spreading of molar flux which completely agrees on the physics of the system.Fig.12 demonstrated the mean concentration distribution against the axial distance.As evident from Fig.12,larger diffusivity makes continuous spreading of solute in the radial direction,resulting in a decrease in peak height of mean concentration.

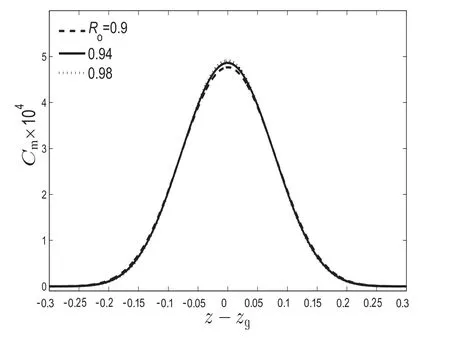
Fig.10.Variation of mean concentration distribution,at a given instant t=1.5 for the case when τy=0.04,m=1.1, β=1,Dp=Dc=1.

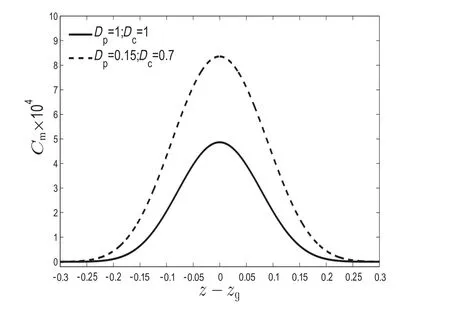
Fig.12.Variation of mean concentration distribution,at a given instant t=1.5 for the case when τy=0.04,R o=0.94,m=1.1, β=1.

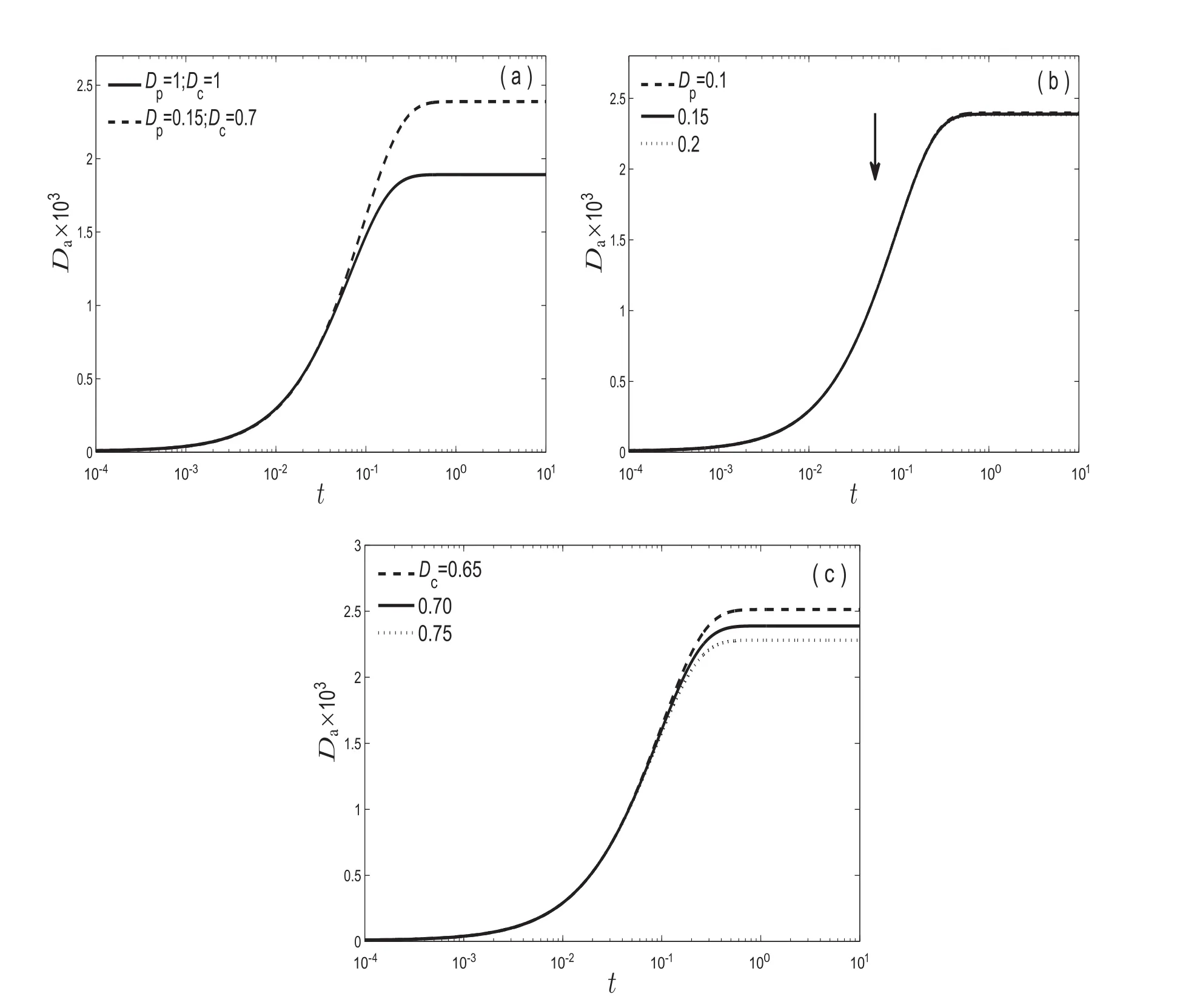
Fig.11.Variation of dispersion coefficient(D a)with time for various values of diffusivity for the case when τy=0.04,R o=0.94,m=1.1, β=1.(b)for D c=0.7(c)for D p=0.15.

The study of dispersion facilitates in understanding the transport of nutrients in blood and various artificial devices[45,46].The investigation of dispersion under the proposed model can be deemed to provide an insight to comprehend the pathological conditions in the cardiovascular system.Our main objective is to understand the physical mechanism of contaminant mixing or to provide a theoretical framework to interpret the spreading of contaminant in a steady blood-like liquid flow with irreversible wall reaction.Mathematical study on blood flow is greatly supported by the Casson model and when the peripheral layer comes into picture it is more convenient for the analysis.The plug flow region within the Casson liquid region is very important as the significant advantages of transporting particulate materials in a plug form are low energy consumption,low particle attrition and low pipe erosion[47].Because ofthe presence ofa peripherallayer,different diffusivity has to be considered and a new parameterviz.,viscosity ratio appears in the study ofsolute dispersion which is very importantfor the studies related to morphology[48].The results of the present study clearly establish the rightful significance to understand the correlation between the flow and the dispersion in an arterial blood flow situation.

8.Conclusions

From the previously stated discourse,it can be readily concluded that the utility of the updated scientific modeldescribed in this paper has a significance in the study of solute dispersion.For all time analysis,the Aris-Barton ‘method of moment’has been performed on the time developed transport coefficients qualitatively and quantitatively,where a two-liquid model has been considered through a rigid pipe under catalytic wall reaction.Again,the‘generalized dispersion model’of Sankarasubramanian and Gill has been employed and the results obtained from both methods are identical,which ensures the authenticity of the results obtained in this study.Mathematical studies on blood flow were mostly studied by the Casson model,but the presence of a peripheral layer on blood has already been accomplished experimentally by different authors.The importance of a peripheral layer on blood flow has been mentioned by few authors while studying resistance to flow,wall shear stress,plug core radiusetc.So,the study of dispersion under such kind of situations has an important physical acceptance.

The following general conclusions can be made from the study:

(i)For all time period,the magnitude of exchange and convection coefficient increases for increasing absorption rate at the pipe boundary though larger absorption makes smaller dispersion coefficient and reaches to its steady value in a short duration of time.

(ii)The exchange coefficient is independent of the yield stress,viscosity ratio,and peripheral layer thickness.

(iii)Whatever be the solvent(purely Casson liquid or three-layer liquid),the values of convection and dispersion coefficients always decrease as yield stress and viscosity ratio increase.

(iv)The presence of a peripherallayerresults in a rise in the values of convection and dispersion coefficients as compared to single layer Casson liquid flow.

(v)Stronger absorption leads to flat the mean concentration distribution and also the peak of the mean concentration distribution increases when yield stress and viscosity ratio increase.

(vi)The convection and dispersion coefficients both decrease as the peripheral layer thickness decreases.

(vii)As diffusivity increases,dispersion coefficient decreases,consequently the peak of the mean concentration distribution also goes downward.

(viii)The findings of the study are also in agreement with those of existing works.

Future Scope of Study

The parameters included in the present scope of study have been singularly motivated to emulate the actual nature of the physiological situation arising in blood flow analysis as far as possible from a mathematical perspective.However actual physiological conditions attributing to the case study can be further varied to enhance the fidelity of the established model in further research.

Nomenclature

Bvariable de fined by Eq.(13)

Cconcentration of the solute

C0initial concentration of the solute

Cmmean concentration of the solute

C(p)pth moment of the distribution of solute

D* molecular diffusion coefficient

Daapparent dispersion coefficient for moment method

Dcmolecular diffusivity for Casson flow region

Dnmolecular diffusivity for Newtonian flow region

Dpmolecular diffusivity for plug flow region

fiith dispersion function(i=0,1,2,3,…)

HiHermite polynomials

M0exchange coefficient

M1convection coefficient

M2apparent dispersion coefficient for generalized dispersion model

mviscosity ratio

PePeclet number

Rradius of pipe

Roratio of the central core radius to the normal pipe radius

Rpplug core radius

rradial coordinate

ttime

uaxial velocity along the flow

u0center line velocity

ucaxial velocity for Casson flow region

unaxial velocity for Newtonian flow region

upaxial velocity for plug flow region

zaxial coordinate

zgcentriod

β wall absorption parameter

δijKronecker delta

θ angular coordinate

μcviscosity of the Casson liquid

μnviscosity of the Newtonian

μppth order central moment

ν2skewness

ν3kurtosis

τcshear stress of the Casson liquid

τnshear stress of the Newtonian liquid

τyyield stress

ψ variable de fined by Eq.(13)

Rc(0≤r≤Ro)Casson liquid region

Rn(Ro≤r≤1)Newtonian liquid region

Rp(0≤r≤Rp)plug flow region within Casson liquid region

pressure gradient

Acknowledgement

The authors greatly acknowledge the valuable suggestions and comments by Prof.Pradeep G.Siddheshwar,Bangalore University,Bangalore,India.One of us(Sudip Debnath)is thankful to NIT Agartala whereas(Ashis kumar Roy)is thankful to MHRD,India for financial support for pursuing this work.We thank the referees for useful comments that re fined the paper to the present form.

Appendix.Derivation of velocity profile in the three-layer region

The dimensionless momentum forms of Eqs.(1)-(4)are:

The plug flow velocity counterpartup(r)can be obtained by takingr=Rpin Eq.(A8)as:

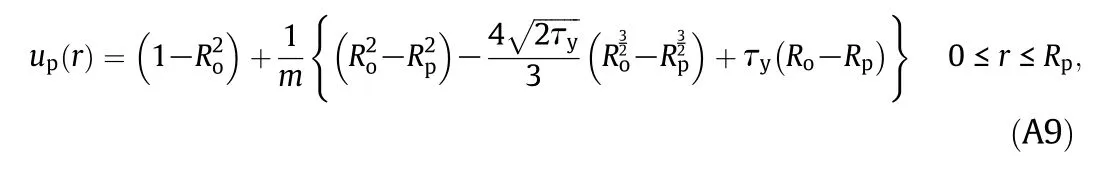
Eqs.(A9),(A8),and(A6)are the velocity distributions in the threelayers documented in Eq.(16).

[1]G.Taylor,Dispersion of soluble matter in solvent flowing slowly through a tube,Proc.R.Soc.London,Ser.A219(1953)186-203.

[2]G.Taylor,Conditions under which dispersion of a solute in a stream of solvent can be used to measure molecular diffusion,Proc.R.Soc.London,Ser.A225(1954)473-477.

[3]R.Aris,On the dispersion of a solute in a fluid flowing through a tube,Proc.R.Soc.London,Ser.A235(1956)67-77.

[4]R.Sankarasubramanian,W.Gill,Unsteady convective diffusion with interphase mass transfer,Proc.R.Soc.London,Ser.A333(1973)115-132.

[5]V.Ananthakrishnan,W.Gill,A.J.Barduhn,Laminar dispersion in capillaries:Part I.mathematical analysis,AlChE J.11(1965)1063-1072.

[6]N.Barton,On the method of moments for solute dispersion,J.Fluid Mech.126(1983)205-218.

[7]J.Rana,P.Murthy,Solute dispersion in pulsatile casson fluid flow in a tube with wall absorption,J.Fluid Mech.793(2016)877-914.

[8]J.Rana,P.Murthy,Unsteady solute dispersion in non-newtonian fluid flow in a tube with wall absorption,Proc.R.Soc.London,Ser.A472(2016)20160294.

[9]B.S.Mazumder,S.Paul,Dispersion of reactive species with reversible and irreversible wall reactions,Heat Mass Transfer48(2012)933-944.

[10]B.S.Mazumder,S.Bandyopadhyay,On solute dispersion from an elevated line source in an open-channel flow,J.Eng.Math.40(2001)197-209.

[11]P.Nagarani,B.Sebastian,Dispersion of a solute in pulsatile non-newtonian fluid flow through a tube,Acta Mech.224(2013)571-585.

[12]B.S.Mazumder,S.K.Das,Effect of boundary reaction on solute dispersion in pulsatile flow through a tube,J.Fluid Mech.239(1992)523-549.

[13]R.Aris,On the dispersion of a solute in pulsating flow through a tube,Proc.R.Soc.London,Ser.A259(1960)370-376.

[14]H.T.Cullinan,On the solution of multicomponent dispersion problems,Chem.Eng.J.5(1973)275-279.

[15]P.G.Siddheshwar,S.Manjunath,Unsteady convective diffusion with heterogeneous chemical reaction in a plane-poiseuille flow of a micropolar fluid,Int.J.Eng.Sci.38(2000)765-783.

[16]E.Marušić-Paloka,I.Pažanin,On reactive solute transport through a curved pipe,Appl.Math.Lett.24(2011)878-882.

[17]I.Pažanin,Modeling of solute dispersion in a circular pipe filled with micropolar fluid,Math.Comput.Modell.57(2013)2366-2373.

[18]A.Mikelic,V.Devigne,C.Van Duijn,Rigorous upscaling of the reactive flow through a pore,under dominant peclet and damkohler numbers,SIAM J.Math.Anal.38(2006)1262-1287.

[19]S.Paul,Effect of wall oscillation on dispersion in axi-symmetric flows between two coaxial cylinders,ZAMM-J.Appl.Math.Mech.91(2011)23-37.

[20]S.Bandyopadhyay,B.S.Mazumder,On contaminant dispersion in unsteady generalised couette flow,Int.J.Eng.Sci.37(1999)1407-1423.

[21]S.Bandyopadhyay,B.S.Mazumder,Unsteady convective diffusion in a pulsatile flow through a channel,Acta Mech.134(1999)1-16.

[22]A.Sarkar,G.Jayaraman,The effect of wall absorption on dispersion in oscillatory flow in an annulus:application to a catheterized artery,Acta Mech.172(2004)151-167.

[23]B.S.Mazumder,K.K.Mondal,On solute transport in oscillatory flow through an annular pipe with a reactive wall and its application to a catheterized artery,Q.J.Mech.Appl.Math.58(2005)349-365.

[24]M.K.Sharp,Shear-augmented dispersion in non-newtonian fluids,Ann.Biomed.Eng.21(1993)407-415.

[25]S.Agrawal,G.Jayaraman,Numerical simulation of dispersion in the flow of power law fluids in curved tubes,Appl.Math.Modell.18(1994)504-512.

[26]R.Dash,G.Jayaraman,K.Mehta,Shear augmented dispersion of a solute in a casson fluid flowing in a conduit,Ann.Biomed.Eng.28(2000)373-385.

[27]P.G.Siddheshwar,S.Markande,S.Manjunath,Effect of interphase mass transfer on unsteady convective diffusion:Part I,plane-poiseuille flow of a power-law fluid in a channel,Chem.Eng.Commun.180(2000)187-207.

[28]P.G.Siddheshwar,S.Markande,S.Manjunath,Effect of interphase mass transfer on unsteady convecttve diffusion:Part II hagen poiseuille flow of a power law fluid in a tube,Chem.Eng.Commun.180(2000)209-229.

[29]P.Nagarani,G.Sarojamma,G.Jayaraman,Exact analysis of unsteady convective diffusion in casson fluid flow in an annulus-application to catheterized artery,Acta Mech.187(2006)189-202.

[30]C.Tu,M.Deville,Pulsatile flow of non-newtonian fluids through arterial stenoses,J.Biomech.29(1996)899-908.

[31]Q.Long,X.Xu,K.Ramnarine,P.Hoskins,Numerical investigation of physiologically realistic pulsatile flow through arterial stenosis,J.Biomech.34(2001)1229-1242.

[32]G.S.Blair,An equation for the flow of blood,plasma and serum through glass capillaries,Nature183(1959)613-614.

[33]S.Charm,G.Kurland,Viscometry of human blood for shear rates of0-100,000 sec-1,Nature206(1965)617-618.

[34]G.Bugliarello,J.Sevilla,Velocity distribution and other characteristics of steady and pulsatile blood flow in fine glass tubes,Biorheol.7(1970)85-107.

[35]G.R.Cokelet,The rheology of human blood,Biomech.Found.Obj.72(1972)63-103.

[36]V.Srivastava,M.Saxena,Two-layered model of casson fluid flow through stenotic blood vessels:applications to the cardiovascular system,J.Biomech.27(1994)921-928.

[37]D.Sankar,A two- fluid model for pulsatile flow in catheterized blood vessels,Int.J.Non Linear Mech.44(2009)337-351.

[38]D.Sankar,U.Lee,Two- fluid casson model for pulsatile blood flow through stenosed arteries:A theoretical model,Commun.Nonlinear Sci.Numer.Simul.15(2010)2086-2097.

[39]J.Shukla,R.Parihar,Dispersion through a flowing fluid with variable viscosity and diffusion coefficient,Phys.Fluids23(1980)1271-1273.

[40]J.Shukla,S.Gupta,Dispersion in a bingham plastic fluid:Effects of peripheral layer,Rheol.Acta21(1982)713-719.

[41]D.A.Anderson,J.C.Tannehill,R.H.Pletcher,Computational fluid mechanics and heat transfer hemisphere,New York,1984.

[42]R.Mehta,R.Merson,B.McCoy,Hermite polynomial representation of chromatography elution curves,J.Chromatogr.A88(1)(1974)1-6.

[43]D.A.McDonald,Blood flow in arteries,Edward Arnold,London,1974.

[44]P.Nagarani,G.Sarojamma,G.Jayaraman,Effect of boundary absorption in dispersion in casson fluid flow in a tube,Ann.Biomed.Eng.32(2004)706-719.

[45]G.Jayaraman,A.Lautier,B.-M.Hung,G.Jarry,D.Laurent,Numerical scheme for modelling oxygen transfer in tubular oxygenators,Med.Biol.Eng.Comput.19(1981)524-534.

[46]S.Middleman,Transport phenomena in the cardiovascular system,John Wiley&Sons,1972.

[47]S.Shaul,H.Kalman,Three plugs model,Powder Technol.283(2015)579-592.

[48]B.D.Favis,J.-P.Chalifoux,The effect of viscosity ratio on the morphology of polypropylene/polycarbonate blends during processing,Polym.Eng.Sci.27(1987)1591-1600.