Experimental detection of bubble-wall interactions in a vertical gas-liquid flow☆

Xing Wang ,Jiao Sun ,3,Jie Zhao ,Wenyi Chen ,*

1 Department of Process Equipment and Control Engineering,Hebei University of Technology,Tianjin 300130,China

2 Research Center of Engineering Fluid and Process Enhancement,Hebei University of Technology,Tianjin 300130,China

3 Department of Mechanics,School of Mechanical Engineering,Tianjin University,Tianjin 300350,China

4 State Key Laboratory of Coal-based Low Carbon Energy,ENN Science&Development Co.,Ltd.,Langfang 065001,China

1.Introduction

Bubble dispersion near wall plays a central role in many industries like chemical engineering,petroleum,food,and pharmaceutical industry.Bubble distribution has a significant effect on strengthening mass and heat transfers and mixing the gas and the liquid in bubble columns,bioreactors and wastewater treatment,etc.It is well known that the wall effect,combined with the wake instability,may cause a more complex path instability forthe rising bubbles.Therefore,ithas practical significance to study the motion of near-wall bubbles and flow characteristics in gas-liquid flow systems for the design and optimization of the processes accompanied with bubble flows.

The rise of a bubble driven by buoyancy in a still liquid has been investigated mainly for the trajectory and shape.The inertia,viscosity,surface tension,and also the contamination of the bubble surface were key factors for the bubble movementwhich were successfully explained by Clift[1].In stagnant and clean water,a small bubble whose diameter was less than 1.3 mm could keep a spherical shape and rise in a straight line.Zenit&Magnaudet[2]found that the so-called path instability was attributed to the asymmetry of the vortical structures in the wake.However,as the bubble size increased,its shape began to deform to ellipsoidal,oblate ellipsoidal,or cap shape,and proceeded in a zigzagging,helical,or more complex movement.In many practical situations,the rising bubbles would encounter incline or vertical wall.Some scholars researched bubbles near inclined wall in the past many years[3-8].Recent theoretical and experimental studies on the near-wall bubbles in gas-liquid flow attracted widespread attention.Chen binet al.[9,10]focused on the trajectory of near-wall bubbles in low and high viscosity liquids.They demonstrated that the existence of the wall could restrain the velocity component by direct numerical simulation.Sygioka and Komori[11,12]developed a new mathematical model and numerical simulation procedures aboutnear-wall bubbles.De Vries[13]explained the motion characteristic of a spherical bubble near a plane wall in pure water using direct numerical simulation and optical experiments.According to their reports,the wake vortex gradually evolved into vortex blob when the bubble collided with a vertical wall.The parameter determining the transition from a straight ascending to a zigzag trajectory was the Weber number.Takemura and Magnaudet[14,15]investigated the motion of a spherical bubble moving near a plane wall in a quiescent water and silicone oils at small Reynolds number(Re≤30),in which the viscous effect was dominant,the rising bubble migrated away from the wallunderrepulsive liftforce caused by diffusion of the vortex in the interaction between the walland bubble wake.But asReincreased,the boundary layer on bubble surface became thinner and liquid velocity was reduced between the bubble and the wall.Due to the velocity distribution,wall-normal pressure gradient around the bubble caused the bubble to be attracted towards the wall.In recent years,based on the conclusions of Takemura and Sugiyama[16]showed that a deformed bubble near the vertical plane had lateral migration in viscous liquid numerically.When the gap between the wall and the bubble became narrower,the bubble bounced off the wall because of the interaction effects of attraction and repulsive lift.Zenget al.[17,18]discussed lift and drag coefficient of a rigid sphere near wall.They revealed that lift coefficient decreased withReand the distance between the wall and the bubble forRe＜100,while the lift coefficient increased forRe＞100.Sugioka and Tsukada[19]obtained similar conclusions by numerical calculation hereafter.

In summary,the main research approaches of flow structure about near wall gas-liquid two-phase flow were numerical simulations and the conclusions were limited to continuous phase around single bubble.The optical experiments of predecessors were primarily interested in the bubbles'trajectory and the effects of attraction and repulsion in the process of bubble rising.Few scholars cared for the motion characteristics of bubble chains and the velocity field around bubbles near the vertical plane wall.Therefore,in the present study,the bubbles'motion characteristics rising with an in finitesimal deformation were discussed by high speed photography technology and the statistical characteristics ofthe flow field around the bubbles were experimentally investigated by the particle image velocimetry(PIV)measurement.The effect of bubble injecting frequency and the distance between the bubble and the plane wall on bubble motions and flow field characteristics such as statistical bubbles'trajectories,average velocity distributions of flow field and Reynolds shear stress,were analyzed.

2.Experimental Set-up and Method

As illustrated in Fig.1,an acrylic cube container(220×220×350 mm3)with a stainless steel nozzle(inner diameter of 0.8 mm)located at the center of the bottom and a detachable glass vertical plane was used in the experiment.The 40%glycerin aqueous solution(ρl=1087.1 kg·m-3,γ =0.0666 N·m-1,μ =3.203 × 10-3Pa·s)has already been filtered,because contaminated liquid would affectbubbles'dynamic characteristics[20-22].A chain of bubbles,generated from compressed air through the nozzle,rose due to buoyancy in quiescent liquid.The frequency ofbubble generation was controlled by a pressure regulatorin the following two situations:bubbles rising freely and near the vertical wall.The four differentinjecting frequencies ofbubbles weref1=47 Hz,f2=126 Hz,f3=157 Hz andf4=210 Hz.The vertical wall was moved horizontally to change the distanceSbetween the nozzle and the wall,asS1=1.5 mm,S2=3 mm andS3=4.5 mm.Therefore,there were totally 16 working conditions in the experiment.The illumination of the test region was provided by an LED light behind the rectangular tank,installed with a piece of sulfuric acid paperas a lightdiffuse.The bubble behavior was recorded by a high-speed camera(2048×2048 pixels),and 10,000 images were obtained continuously at a frame rate of 100 Hz.The image sequences obtained were analyzed by a digital image processing algorithm based on MATLAB software.Fig.2 showed the original photos of two bubbles taken in the experiment.The circle in Fig.2 around the bubble was the result of ellipse fitting of the bubble after processing with MATLAB.

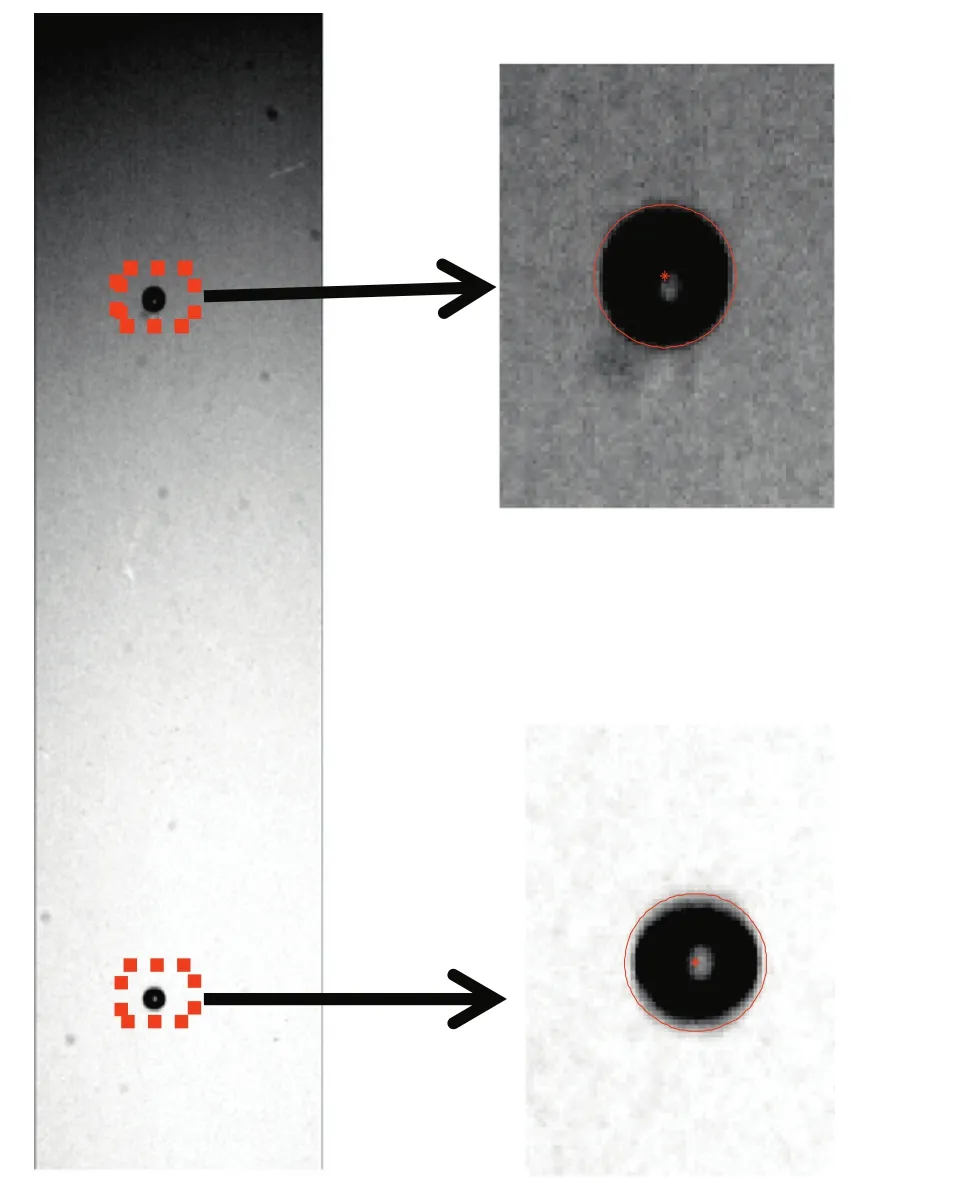
Fig.2.The original photo of bubbles taken in the experiment.

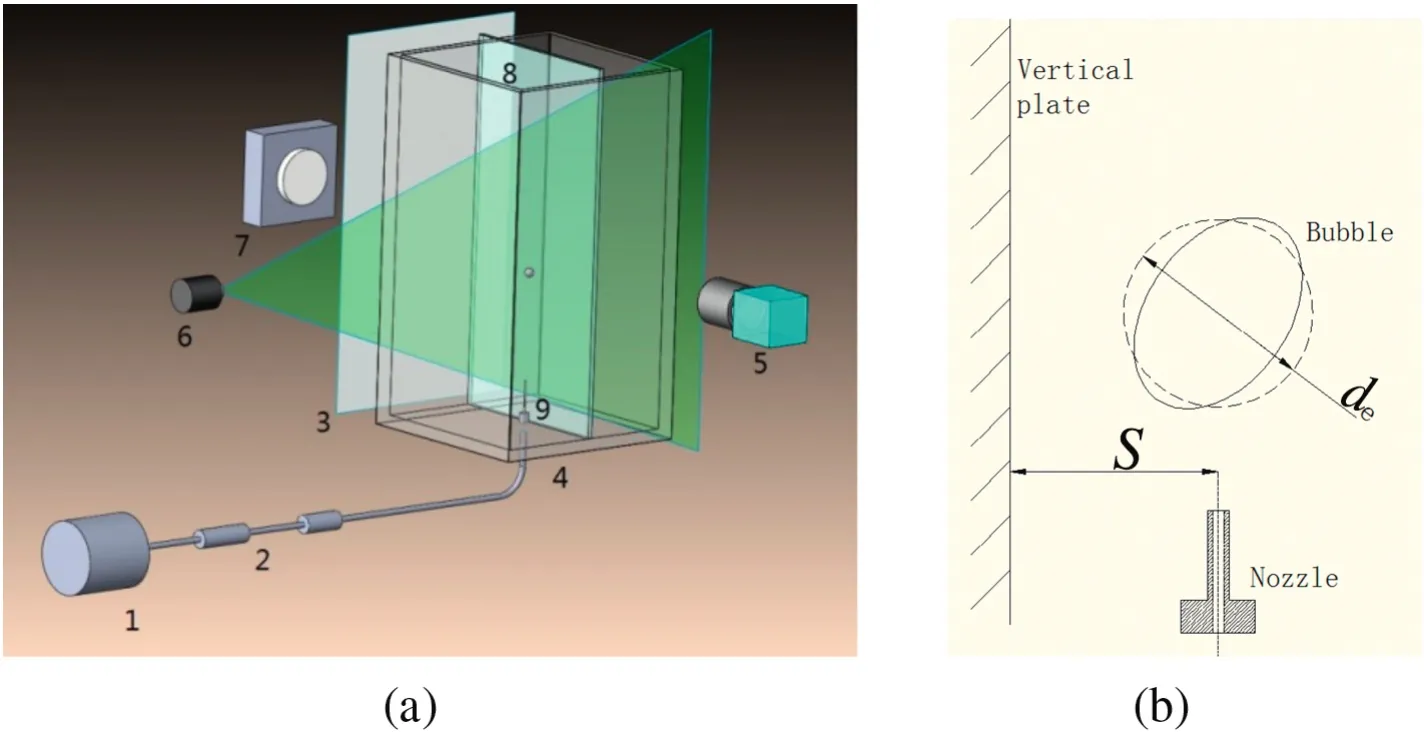
Fig.1.Sketches of experiment system:1.Air pump,2.Press regulator,3.Diffuser plate,4.Water tank,5.CCD camera,6.Laser,7.LED light,8.Vertical plane wall,9.Nozzle.

To investigate the flow field ofgas-liquid flow,time-resolved particle image velocimetry(TR-PIV)system(LA Vision)was implemented.The laser(100 mJ)plane was aligned vertically to induced fluorescence of Red fluorescent polymer microspheres seeded in the flow,with the density of1050 kg·m-3and the diameterof20-50μm.Particle images were recorded by a high-speed camera with a resolution of2048×2048 pixels at the sampling rate of 100 Hz.10,000 samples data and 9999 instantaneous velocity fields were obtained in the experiment.The final interrogation window had a size of 32×32 pixels and an overlap ratio of 75%.Table 1 showed the details of different experimental conditions,thatRe=Vtdeρlμ-1,Eo=g(ρl- ρg)de2γ-1andMo=(ρl- ρg)gμ4/γ3ρl2.Here,ρland ρgare the density of glycerin aqueous solution and air,respectively,gis the gravitational acceleration,Vtis the terminal rising velocity of bubble,γ and μ are the surface tension and kinematic viscosity of glycerin aqueous solution,respectively.The original PIV images of rising bubbles in the condition off2=126 Hz were showed in Fig.3,where the bubble was shown to be within a broken red line in the pictures.

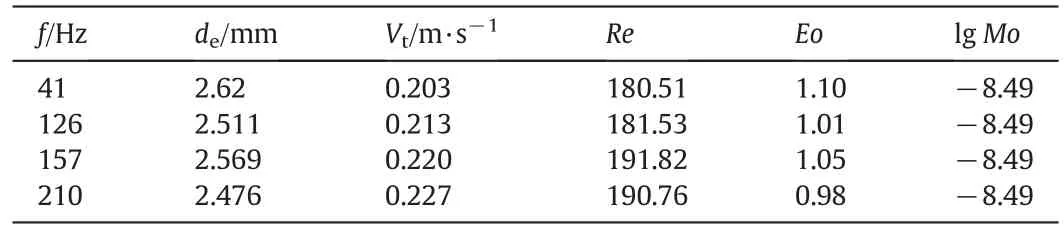
Table 1Experimental conditions

3.Results and Discussion

3.1.Rising behavior of the near wall bubble train

Normally,dimensionless parametersEo,MoandRecan be used to describe the characteristics of bubbles in a stagnant liquid,different shapes of bubbles have differentEoandMo[23-25].Clift[1]researched bubbles in liquids with different physical properties and drew a classic diagram,shown in Fig.4,which could describe differentbubbles related to differentEo,MoandRe.There were three types of bubble rising,i.e.rectilinear,zigzag and spiral trajectory[2,10,24-28],both of the last two unsteady motion was mainly caused by asymmetric distributions of the vortical structures behind the bubbles.Subsequently,some researchers studied the relation of dimensionless parameters in different viscosity liquids by numerical simulation and experimental method.The results were in good agreement with the result of Clift[10,29,30].In the experiment,a suitable inner diameter of nozzle and glycerin aqueous solution with special concentration were prepared to ensure bubbles ascending in a straight line.The enlarged black points in Fig.4 represented four different emission frequencies in the experiment,from which it could be seen that the bubbles in this region were nearly elliptical.

Fig.5(a)showed the statistical trajectory of a chain of bubbles rising without wall under the condition of four different frequencies.In the figure,x=0 represented the location of nozzle,andy-axis represented the vertical distance above the nozzle surface.As can be seen in Fig.5(b),there were three different stages in the process of bubbles rising:acceleration,deceleration and constant velocity.Fig.5(b)showed thatthe bubble terminalvelocity increased with the advance ofthe bubble frequency.The reason was that the bubble frequency was increased by the higher pressure in the gas pipeline,which caused the bubble to have more inertial energy when escaping from the nozzle.So the bubbles with higher frequency had a larger terminal velocity.

Fig.3.The original PIV images of rising bubbles:(a)freely rising bubbles without the plane;(b)S*≈ 1.2;(c)S*≈ 2.3;(d)S*≈ 3.6.

The presence of rigid wall affected the forms of bubble movement,gas hold-up and the structure of the flow field around bubbles.When bubbles rising in straight were affected by rigid wall,not only the surface of bubbles would deform,but also the form of original motion would change.The main forms of nearwall bubble motion included migrating away from the wall,moving towards the wall and bouncing along the wall.The lift force on the bubble played an important role in the movement of the bubble.When the direction of the lift force on the bubble was away from the wall,bubble moved away from the wall.In turn,bubble moved close to the wall.Meanwhile bouncing motion was caused by the direction change in the lift force.

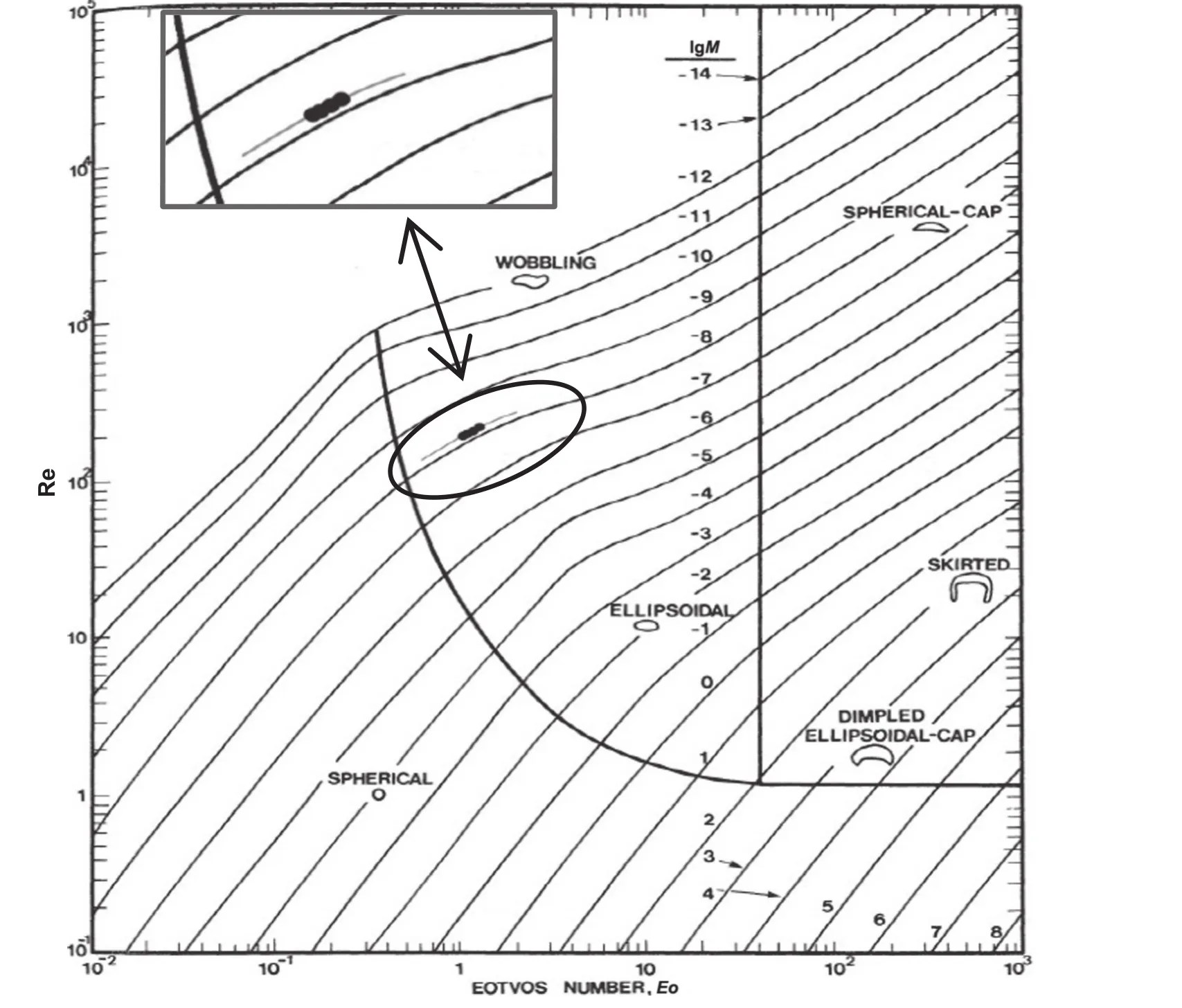
Fig.4.Shape regions of different frequency bubbles in unhindered gravitational motion through stagnant liquids in the experiment[1].

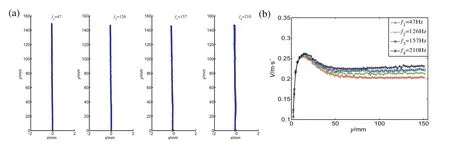
Fig.5.Statistical trajectories(a)and speed curve(b)of freely rising bubbles with four different frequencies.

Bubble motion characteristics were compared under the conditions of different distanceSbetween the vertical plane and the nozzle.When the normalized initial distanceS*≈1.2,bubbles ascended in zigzag trajectory and the trajectory of all bubbles overlapped greatly,as shown in Fig.6.The vertical wall was located in the negativex-axis.The first bouncing happened when the bubble collided with the wall after escaping from the nozzle and then bubbles ascended in zigzag trajectory.Meanwhile,all bubbles with different frequencies had a tendency to migrate away from the wall.Theoretically,bubble motion characteristic was in fluenced by the combined effect of both inertial force and lift force when the bubble escaped from the nozzle.In the experiment,the frequency of the bubbles was controlled by adjusting the pressure regulator.With the augment of pressure,the frequency of the bubbles would gradually increase.From the perspective of qualitative analysis,the speed of bubbles escaping from the nozzle must be increase gradually,and therefore the inertial force would increase gradually.About the effect of lift force which caused by the wall on bubble motion characteristics,evidence can be found in the literature.Many scholars have used direct numerical simulation to numerically demonstrate the change in the direction of lift force.Zenget al.[17,18]discussed lift and drag coefficient of a rigid sphere near wall.At lowRe,the moment coefficient was negative,but it rapidly increased and became positive even with a small increase inRe.The lift coefficient decreased withReand the distance between the wall and the bubble forRe＜100,while the lift coefficient increased forRe＞100.In addition,vorticity generated on the particle surface was not symmetrically distributed in the wake due to the presence of the nearby wall.The asymmetry in the vorticity distribution contributed to an asymmetric induced flow,whose effectwas to generate a liftforce on the particle directed away from the wall.Sugioka and Tsukada[19]calculated the drag and lift forces acting on a spherical bubble moving near a plane wall over a wide range ofRefrom 1 to 300,and to numerically demonstrate the change in the direction ofliftforce.The main resultsshowed thatthe direction of the lift force on the bubble changed from towards the wall to away from the wall betweenL/d=0.6 and 0.7 when the Reynolds number was larger than 100.Whatcan be con firmed was thatthe direction of the lift force was away from the wall in the present condition.So with the combined effect of inertial force and lift force,all bubbles with different frequencies tended to migrate away from the wall.This was also consistent with the result from the experiment.

Fig.7 showed bubble trajectory with different frequencies whenS*≈ 2.3 andS*≈ 3.6,respectively.WhenS*≈ 2.3,Fig.7(a)revealed that all the bubbles of different frequencies had a tendency to move close to the wallafterescaping from the nozzle when the rising distancey＜20 mm.However,in the location of 20 mm＜y＜60 mm,bubbles moved away from the wall obviously.Furthermore,low-frequency bubbles ascended in straight lines wheny＞60 mm and the distance between the rising bubble and the wall increased gradually.But the increase of that distance was not obvious for bubbles with higher frequency(f4=210 Hz).In Fig.7(b),underS*≈3.6,low-frequency bubbles ascended in straight lines,and also gradually migrated away from the wall,but with the frequency increasing,the bubbles gradually moved towards to the wall.By contrasting Fig.7(a)to(b),at the same frequency,with the increase ofS*,the lateral migration distance of the bubbles decreased gradually.At the sameS*,the lateral migration distance of the bubble also decreased with the increase of the frequency.The wall effect would decrease as the initial distance from the bubbles to the wall increased.WhenS*became larger,the wall effect acting on the bubble would decrease,thatis,the effectofliftforce would decrease,and the increase of frequency caused the inertial force of the bubble to increase.AstheS*and the frequency increased,the proportion ofthe inertial force increased gradually in the combined action of the inertial force and the lift force.If the proportion of the inertial force was greaterthan the lift force,the trajectory of the bubble showed the reduction of lateral migration distance,.i.e.,the bubble moved close to the wall.In summary,the bubble frequency and the normalized initial distance between the bubble and the wall commonly affect the movement of bubbles,so the bubbles also appeared in different motion states in different frequencies and distances.

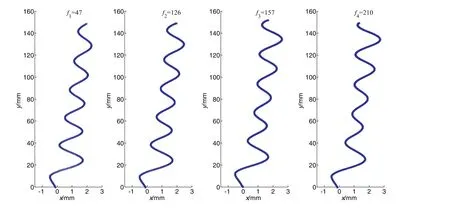
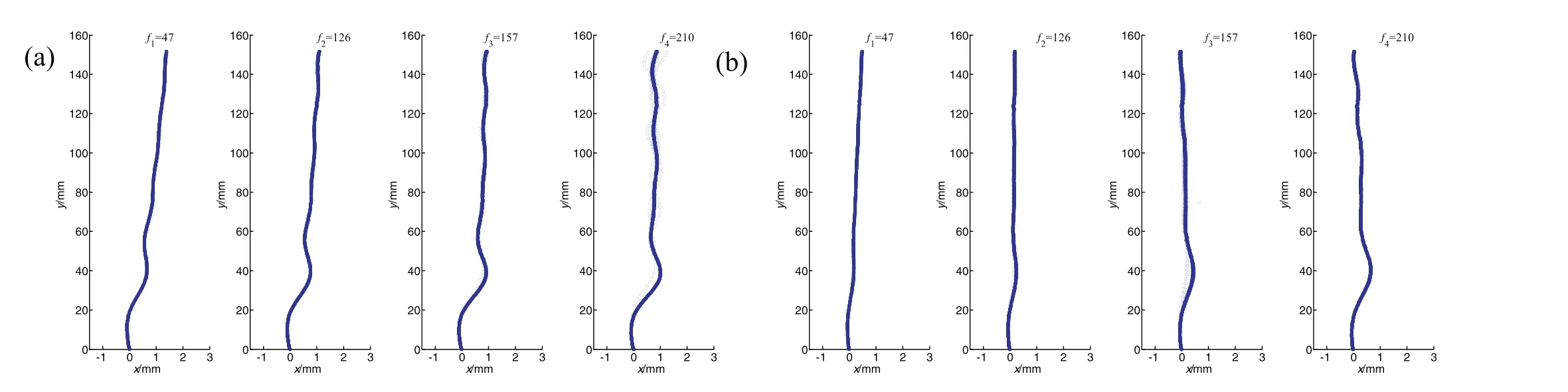
Fig.7.Statistical trajectories of bubbles with(a)S*≈2.3;(b)S*≈3.6.

3.2.Flow characteristics around the near wall bubble

In stagnant liquids,the average flow fields around the bubbles were symmetrical if the bubble ascended in a straight line without wall.When the ejection frequency of bubbles was increased,the average velocity of the liquid around the bubbles became larger,since the higher terminal velocity of bubbles could continuously drive liquid around them,as shown in Fig.8.

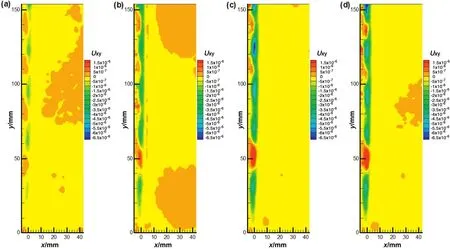
The average velocity distributions of flow field in the case ofS*≈1.2 were shown in Fig.9,where the vertical wall was also located in the negativex-axis.Under the in fluence of bubbles ascending in zigzag trajectory,high and low average velocity flow appeared on both sides of the bubbles,alternating with each other.Furthermore,the liquid was extruded when bubbles moved towards the wall,and the compression effectmade the liquid obtain acceleration.So both drive function of bubbles and compression effect of wall collectively led to high-speed fluid existed in the region between the wall and the nozzle.

The average velocity distributions of flow field with four different bubble frequencies atS*≈2.3 were shown in Fig.10.The regularities of flow field distribution for bubbles moving towards the wall or away from the wall were almost similar.The liquid near wall had relative high velocity,while on the side of far away from the wall it had relative low speed.Because of repressive effect of the wall,the liquid driven by rising bubbles could only change little momentum with low-speed liquid,even including stagnantliquidsin the region between the bubble and the wall.However,the liquid on the side far away from the wall could change more momentum with low-speed and stagnant liquid by the driven of bubbles.Therefore,there was a phenomenon of asymmetrical velocity distribution on both sides of the bubbles.

In the present,the schemes only considered the flow distributions in the laser sheet,and the results could show the flow regularity around the bubbles[31,32].However,the flow- fields information out of the lasersheetshould notbe ignored.So in the future itshould be measured by other means,e.g.Tomographic PIV,which could help us to see more details of the two-phase flow near the vertical wall.

3.3.Reynolds shear stress and turbulent intensity around the near wall bubble

It was well known that Reynolds stress was generated by turbulent fluctuation.In industry production,the size and the distribution of shear stress affected the efficiency of heat exchange and mass transfer.Therefore,itwas significantto study Reynolds shearstress characteristic of near wall gas-liquid two-phase flow.

The shear stress distributions on both sides of bubbles were symmetrical when bubbles rose without plane wall,as shown in Fig.11.In the wake vortex behind bubbles,the fluid flow directions were opposite,which led positive and negative magnitude of shear stress.As the bubble frequencies increased,liquid surrounding bubbles was driven more frequently,which made higher shear stress of the liquids around bubbles.

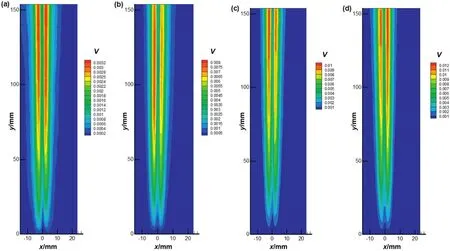
Fig.8.The average velocity distribution of flow field around freely rising bubbles:(a)f1=47 Hz;(b)f2=126 Hz;(c)f3=157 Hz;(d)f4=210 Hz.

Fig.12 showed the shear stress distribution for different bubble frequencies atS*≈1.2.In this condition,bubbles rose at the zigzag trajectory,and the shapes of the stress distribution looked like blobs.The Reynolds stress distributions were characterized by the alternate positive and negative variations,which were accorded with bubbles ascending in zigzag trajectory.Meanwhile,shear stress magnitudes in the vicinal region near wall were higher than that far from the wall.The blob structure of shear stress was generated only when bubbles ascended atzigzag trajectory nearthe wallbecause thiskind ofsituation could form alternative vortex motion in the wake of bubbles.Although the shear stress magnitude with bubbles at low frequency was small,the blob structures were obvious.The reason for this phenomenon was that the interval between two bubbles of low frequency was bigger than that of high frequency.Thus the vortex structure induced by the first bubble could exist a long time without being destroyed by the next bubble.Nevertheless,the vortex structures induced in the risingprocess of high frequency bubbles were easily destroyed by later bubbles.Thus there were regularities of distribution for Reynolds shear stress in Fig.12.

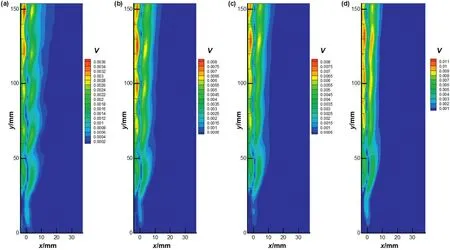
Fig.9.The average velocity distribution of flow field around rising bubbles at S*≈1.2:(a)f1=47 Hz;(b)f2=126 Hz;(c)f3=157 Hz;(d)f4=210 Hz.

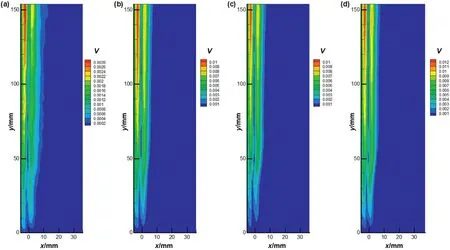
With the increase of bubble frequencies,there were large-scale Reynolds stresses in unsteady stage(20 mm＜y＜60 mm)of the rising bubbles atS*≈2.3,which was seen in Fig.13.It illustrated that there was higher pulsation speed of liquid between the vertical wall and the bubble when near wall rising bubbles lose its stability.In the following rising process,the Reynolds stresses far away from the wallwere higher than that in the region of near wall.It was because that repressive effect of rigid wall would cause the fluid layer to have high mean velocity,while the liquid far away from the wall was less affected by repressive effect and high-speed fluid was easy to move into the fluid layer with smaller mean velocity.Owing to this mechanism,the low-velocity fluid layer was accelerated and higher Reynolds stresses appeared in away from the wall.

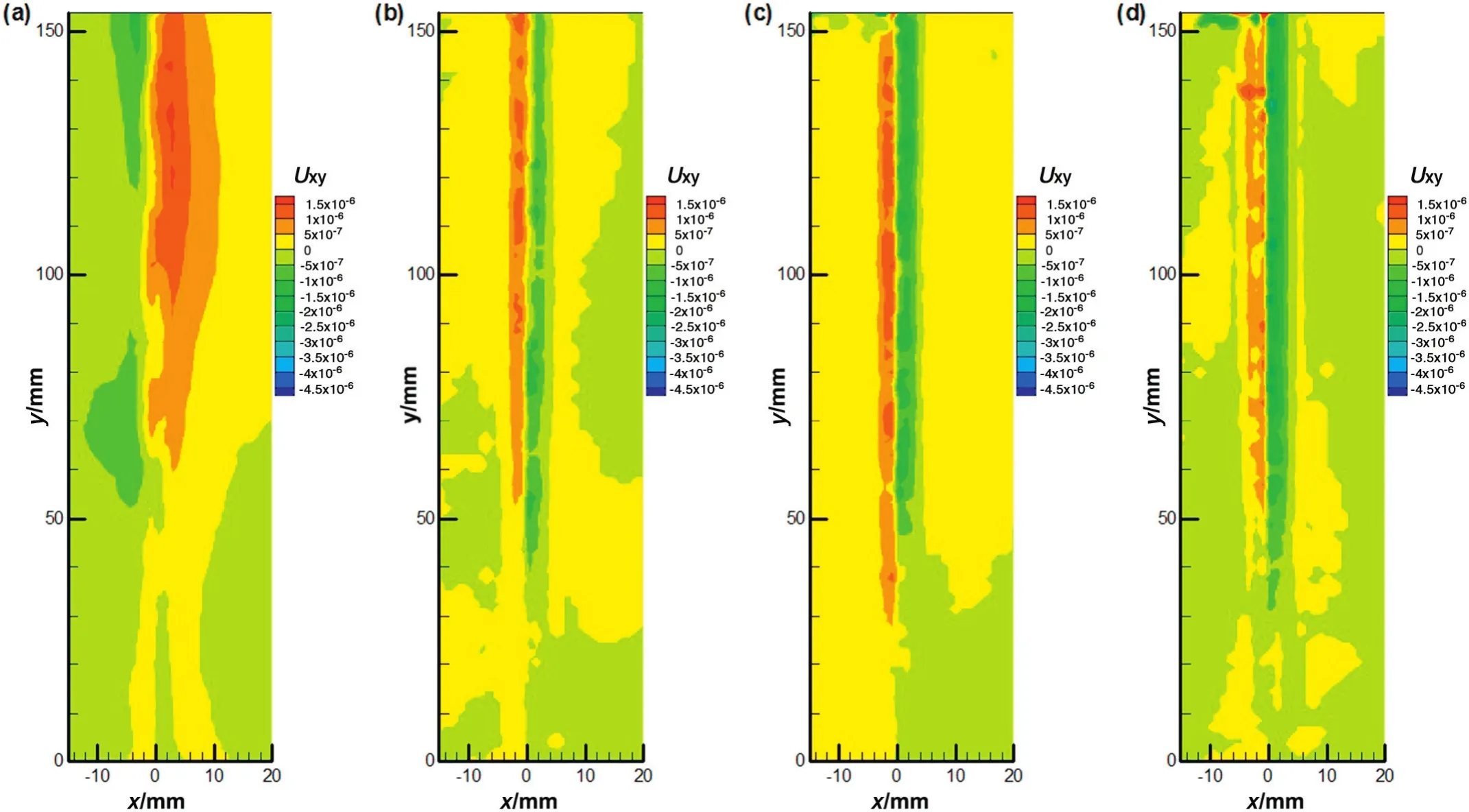
Fig.11.The shear stress distribution for freely rising bubbles:(a)f1=47 Hz;(b)f2=126 Hz;(c)f3=157 Hz;(d)f4=210 Hz.

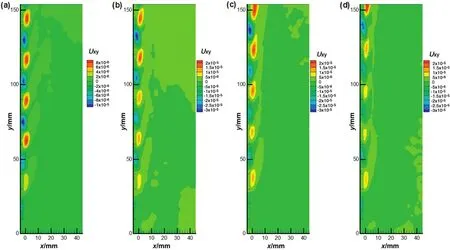
Fig.12.The shear stress distribution for rising bubbles at S*≈1.2:(a)f1=47 Hz;(b)f2=126 Hz;(c)f3=157 Hz;(d)f4=210 Hz.

Fig.14 showed the in fluence of normalized initial distanceS*and bubble ejecting frequency on the turbulent intensity profiles.It was noted that the turbulent intensity profiles were almost symmetrical aboutx=0 for freely rising bubbles with different frequencies.In Fig.14 the peaks became higher as the bubble frequency increased and it was also seen that the turbulent intensities in theydirection were greater than that in thexdirection.Furthermore,the turbulent intensity in thexdirection whenS*=1.2 was higher than other cases,which suggested that the bubbles rising in zigzag trajectory facilitated the uniformity ofturbulence distribution.Butthe value ofturbulentintensity inydirection had no obvious change in different situations in Fig.14.

4.Conclusions

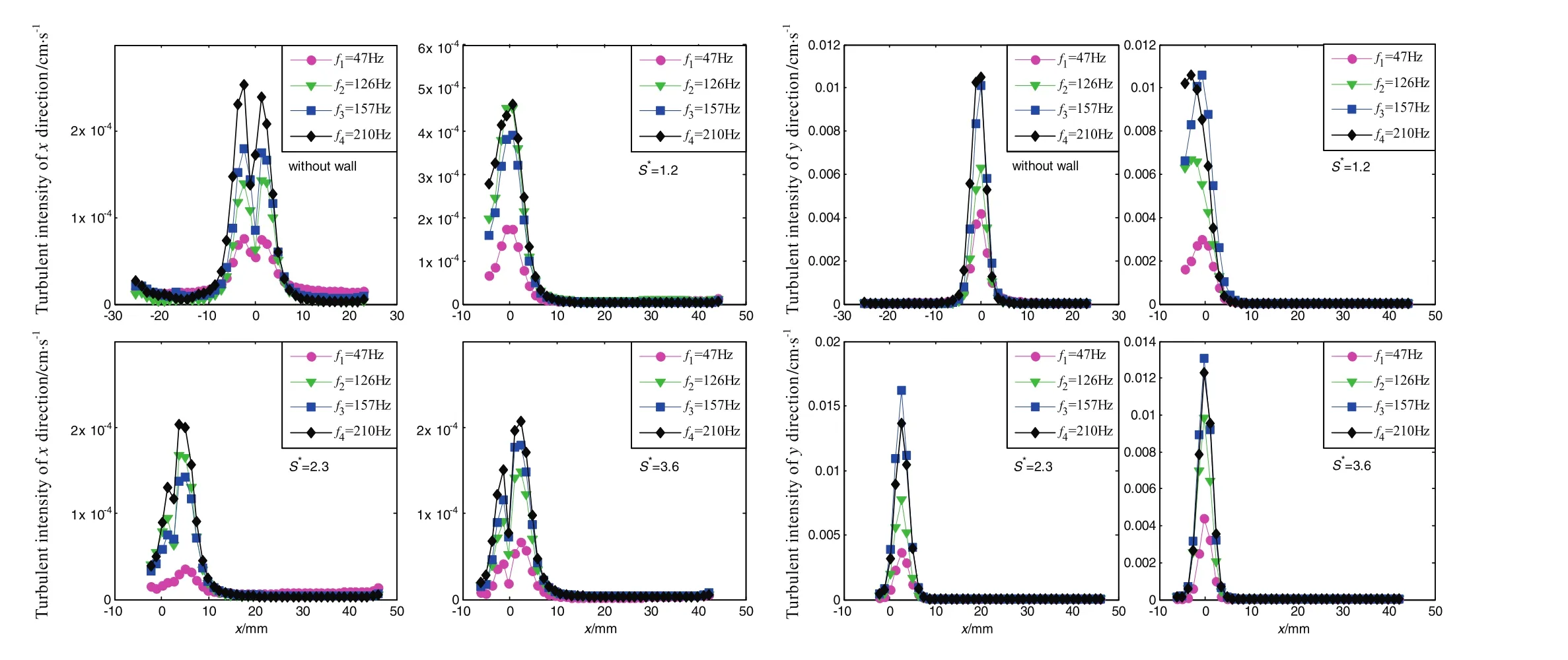
Fig.14.Turbulence intensity profiles in different cases.

The near-wall rising characteristic of bubbles in a chain has been studied and analyzed while varying the normalized initial distance(S*)and bubble frequency(f).In the present experiment,the rising bubbles in a straight line without the wall and more complex path variations due to the wall effectand frequency variation were observed.It is found that near-wall bubble rising trajectory changes from a zigzag path to a smoothly straightline with the increase ofS*.The average flow fields around the bubbles and the turbulentintensity profiles are almost symmetricalwhen bubble ascends in a straightline without wall.When near-wall bubbles ascended in zigzag trajectory,high and low average velocity would alternately appear on both sides of the bubbles,and as well as the positive and negative Reynolds shear stress.For near wall bubbles ascended in analogous straight trajectory,bubbles'trajectory tend to far away or close to the wall,and the fluid between bubbles and the wall has higher velocity and lower Reynolds shear stress.

[1]R.Clift,J.R.Grace,M.E.Weber,Bubbles,Drops,and Particles,Courier Corporation,2005.

[2]R.Zenit,J.Magnaudet,Path instability of rising spheroidal air bubbles:A shapecontrolled process,Phys.Fluids20(2008)061702.

[3]T.Maxworthy,Bubble rise under an inclined plate,Phys.Fluids229(1991)659-674.

[4]A.Perron,L.I.Kiss,S.Poncsák,An experimental investigation of the motion of single bubbles under a slightly inclined surface,Int.J.Multiphase Flow32(2006)606-622.

[5]B.Donnelly,T.S.O'Donovan,D.B.Murray,Surface heat transfer due to sliding bubble motion,Appl.Therm.Eng.29(2009)1319-1326.

[6]B.Chen,Direct numerical simulation of a single bubble rising along an inclination wall,J.Eng.Thermophys.28(2007)965-967(in Chinese).

[7]H.Ju,G.Chen,G.D.Li,et al.,Experimental study on motion behavior of single bubble rising along inclined plane in still water,Chin.J.Hydrodyn.26(2011)327-332(in Chinese).

[8]S.M.Dong,G.D.Li,R.Xue,et al.,Experimental research on collision and rebound of single bubble with inclined wall in stationary liquid,J.Water Resour.Archit.Eng.6(2008)50-52(in Chinese).

[9]B.Chen,Direct numerical simulation of a single bubble rising in still water,J.Eng.Thermophys.26(2005)980-982(in Chinese).

[10]B.Chen,Direct numerical simulation of a single bubble rising in high viscosity fluid,J.Eng.Thermophys.27(2006)255-258(in Chinese).

[11]K.I.Sugioka,S.Komori,Drag and lift forces acting on a spherical water droplet in homogeneous linear shear air flow,J.Fluid Mech.570(2007)155-175.

[12]K.I.Sugioka,S.Komori,Drag and lift forces acting on a spherical gas bubble in homogeneous shear liquid flow,J.Fluid Mech.629(2009)173-193.

[13]A.W.G.De Vries,A.Biesheuvel,L.Van Wijngaarden,Notes on the path and wake of a gas bubble rising in pure water,J.Multiphase Flow28(2002)1823-1835.

[14]F.Takemura,J.Magnaudet,The transverse force on clean and contaminated bubbles rising near a vertical wall at moderate Reynolds number,J.Fluid Mech.495(2003)235-253.

[15]F.Takemura,S.Takagi,J.Magnaudet,et al.,Drag and lift forces on a bubble rising near a vertical wall in a viscous liquid,J.Fluid Mech.461(2002)277-300.

[16]K.Sugiyama,F.Takemura,On the lateral migration of a slightly deformed bubble rising near a vertical plane wall,J.Fluid Mech.662(2010)209-231.

[17]L.Zeng,S.Balachandar,P.Fischer,Wall-induced forces on a rigid sphere at finite Reynolds number,J.Fluid Mech.536(2005)1-25.

[18]L.Zeng,F.Najjar,S.Balachandar,et al.,Forces on a finite-sized particle located close to a wall in a linear shear flow,Phys.Fluids21(2009)033302.

[19]K.Sugioka,T.Tsukada,Direct numerical simulations of drag and lift forces acting on a spherical bubble near a plane wall,J.Multiphase Flow71(2015)32-37.

[20]B.Cuenot,J.Magnaudet,B.Spennato,The effects of slightly soluble surfactants on the flow around a spherical bubble J,J.Fluid Mech.339(1997)25-53.

[21]J.Magnaudet,I.Eames,The motion of high-Reynolds-number bubbles in inhomogeneous flows,Annu.Rev.Fluid Mech.32(2000)659-708.

[22]S.Takagi,Y.Matsumoto,Surfactant effects on bubble motion and bubbly flows,Annu.Rev.Fluid Mech.43(2011)615-636.

[23]L.Liu,H.J.Yan,G.J.Zhao,Experimental studies on the shape and motion of air bubbles in viscous liquids,Exp.Thermal Fluid Sci.62(2015)109-121.

[24]D.Mikaelian,A.Larcy,A.Cockx,etal.,Dynamics and morphology of single ellipsoidal bubbles in liquids,Exp.Thermal Fluid Sci.64(2015)1-12.

[25]D.Mikaelian,A.Larcy,S.Dehaeck,A new experimental method to analyze the dynamics and the morphology of bubbles in liquids:Application to single ellipsoidal bubbles,Chem.Eng.Sci.100(2013)529-538.

[26]A.Tomiyama,G.P.Celata,S.Hosokawa,et al.,Terminal velocity of single bubbles in surface tension force dominant regime,Int.J.Multiphase Flow28(2002)1497-1519.

[27]L.J.Xu,G.Chen,J.B.Shao,et al.,Study on motion behavior of bubbles with different diameters in still water,Chin.J.Hydrodyn.27(2012)582-588(in Chinese).

[28]R.Zenit,J.Magnaudet,Measurements of the streamwise vorticity in the wake of an oscillating bubble,Int.J.Multiphase Flow35(2009)195-203.

[29]H.R.Wang,Y.P.Li,D.Yang,et al.,On the shape feature of a single bubble rising in viscous liquids,J.Eng.Thermophys.9(2009)1492-1494(in Chinese).

[30]M.Wu,M.Gharib,Experimental studies on the shape and path of small air bubbles rising in clean water,Phys.Fluids14(2002)49-52.

[31]Z.L.Liu,Y.Zheng,PIV study of bubble rising behavior,Powder Technol.168(1)(2006)10-20.

[32]Z.L.Liu,Y.Zheng,L.Jia,et al.,Study of bubble induced flow structure using PIV,Chem.Eng.Sci.60(13)(2005)3537-3552.