Infrared thin layer drying of saffron(Crocus sativus L.)stigmas:Mass transfer parameters and quality assessment

Mehdi Torki-Harchegani*,Davoud Ghanbarian ,Vida Maghsoodi,Ahmad Moheb

1 Young Researchers and Elite Club,Shahrekord Branch,Islamic Azad University,Shahrekord,Iran

2 Department of Mechanical Engineering of Biosystems,Shahrekord University,Shahrekord,Iran

3 Department of Chemical and Petroleum Engineering,Sharif University of Technology,Tehran,P.O.Box 11155-9465,Iran

4 Department of Chemical Engineering,Isfahan University of Technology,Isfahan 84156-83111,Iran

1.Introduction

Saffron is the commercial name of the dried stigmas of a flower scientifically identified asCrocus sativusL.It is widely used as a spice in foods[1].Iran is the most important saffron producer in the world with a share of 90%of the total production[2].After harvesting,a dehydration process is necessary to convertC.sativusL.stigmas into saffron spice.To maintain the product quality for a longer time,the moisture content should be reduced at least below 12%[3,4].Drying causes necessary changes in the physical,biochemical,and chemical properties and brings desired attributes of saffron.The main attributes that determine the market value and quality of saffron are color,aroma,and taste and the compounds responsible for these attributes are crocins,safranal and picrocrocin,respectively[5].The effect of different drying on these components has been studied by some researchers[1,2,5,6].

Generally,the dehydration methods are classified as traditional and industrial drying.Open sun and shade drying are the traditional methods still widely used because of their simplicity and low investment costs[7].These drying methods are still used in Iran,India and Morocco for saffron stigmas drying.However,these methods pose some problems such as long drying time,and dust and microbial contamination of the dried materials[8].Artificial drying methods are carried out at higher temperatures and have been employed in saffron processing in some countries such as Spain,Greece,and Italy[5].In spite of some advantages for industrial dryers,including achievement of hygienic conditions,quality control and reduction of product loss and process duration,energy requirement in drying technology is one of the key problems that should be overcame.The drying process generally consumes large amounts of energy and releases carbon oxides to the environment.Therefore,it is crucial not only to assurance for good quality of the dried products but also high energy efficiency and low environmental impact[9].

Infrared radiation(IR)is one of the increasingly popular methods for supplying heat for drying of moist materials.The IR is known as an artificial drying method increases the moist material temperature and evaporates its moisture by action of infrared wavelength radiation from a source that interacts with the internal structure of the product.The IR heating presents some advantages such as decreasing drying time,high-energy efficiency and lower environmental impact.The energy of radiated waves is transferred from the source to the sample product without heating surrounding air leading to higher temperature in the inner layers of the samples in compared to the surrounding and more heat transfer[10].

To design new dryers or improve the existing ones,and control the drying systems,mathematical models are used to model and simulate the drying process[11].Theoretical,semi-theoretical and empirical models are the main proposed mathematical models used to describe the drying behavior of agricultural materials[12].Theoretical simulations are realistic and can give an explanation for phenomena occurring during drying process but,they are more difficult and require a substantial amount of computing time due to the complexity of diffusion equations governing the process[13].The empirical models derive a direct correlation between average moisture content and drying time and neglect the drying process fundamentals[12].The semitheoretical models offer a compromise between theory and ease of application and are generally derived from direct solution of Fick's second law by assuming some simplifications[14].

Considerable studies have been carried out to drying and also to determine moisture diffusion and convective moisture transfer coefficient of agricultural products.Nonetheless,very rare researches have been reported about saffron drying kinetics[15,16]and,to the best of our knowledge,no information about mass transfer parameters of saffron stigmas is available in the literature.

The main objectives of the present study were to investigate the infrared drying kinetics of saffron stigmas at different temperatures,determine the mass transfer parameters(effective moisture diffusivity and convective mass transfer coefficient)and assess the quality characteristics of saffron stigmas.

2.Materials and Methods

2.1.Dehydration experiments

Full-bloomedC.sativusL. flowers were picked from farms in Torbathheydariye,Northeast Iran(35°16′N and 59°14′E),and stored in a refrigerator at 4°C until the experiments were started.The stigmas for the experiments were separated by hand from the flowers at 24°C indoors.The average initial moisture content of the stigmas was determined using oven drying at 103°C and atmospheric pressure,and approximately obtained to be 4.26 g water per gram dry matter.The drying experiments were carried out with infrared waves,using a Shimadzu Electronic Moisture Balancer Model LIBROR EB-340MOC at six different temperatures of 60,70,80,90,100 and 110°C.For each experiment,5 g of the fresh stigmas was distributed uniformly in the instrument pan in a thin layer with about 0.7 mm thickness.The moisture loss was recorded at 2 min intervals during drying process and the experiments were continued until the samples lot was dried to the final moisture content of about 0.1 g water per gram dry matter.At each drying temperature,the experiments were replicated three times and the average values were used[15].

2.2.Determination of mass transfer parameters

The main mechanism of moisture transfer during drying of most biological materials is liquid and/or vapor diffusion[17].Assuming isotropic behavior of the samples with regard to the water diffusivity,Fick's second law of unsteady state diffusion is used to describe the moisture movement in drying process as follows[16]:

Many authors have used Crank's solution of the Fick's second law of diffusion for different shaped materials to determine the effective moisture diffusivity[10,18–20].In the present study,the Dincer and Dost model was performed to determine moisture transfer parameters of saffron stigmas undergoing infrared treatment.Dincer and Dost[21,22]presented a solution for one-dimensional transient equation for different geometric shaped moist objects by applying the following assumptions[21,22]:

–Constant thermo-physical properties for the solid object and drying fluid,

–Ignoring effect of heat transfer on mass transfer and,

–Occurring of moisture diffusivity in the radial direction in the solid cylinder and sphere,and in the thickness direction in the slab.

Applying these conditions,the equation and its initial and boundary conditions for a slab are written in the following form:

whereDis the effective moisture diffusivity(m2·s−1),kis the convective mass transfer coefficient(m·s−1),tis drying time(s),yis the distance from the center(m),andLis half thickness of the sample(m).In addition,M,M0,MeandMsare the instantaneous,initial,equilibrium and surface moisture contents of the samples(g water per gram dry matter,g·g−1),respectively.

The solution of Eq.(2)with the governing initial and boundary conditions yields dimensionless moisture ratio distribution as the following form:

In Eqs.(8)and(9),μnis then-th root of the transcendental characteristic equation(dimensionless).Also,FoandBiare the Fourier and Biot number,respectively and for a slab with the thickness of 2Lare defined as:

For negligible small values of Fourier number,Eq.(6)can be simpliifed to the first term only[17]:

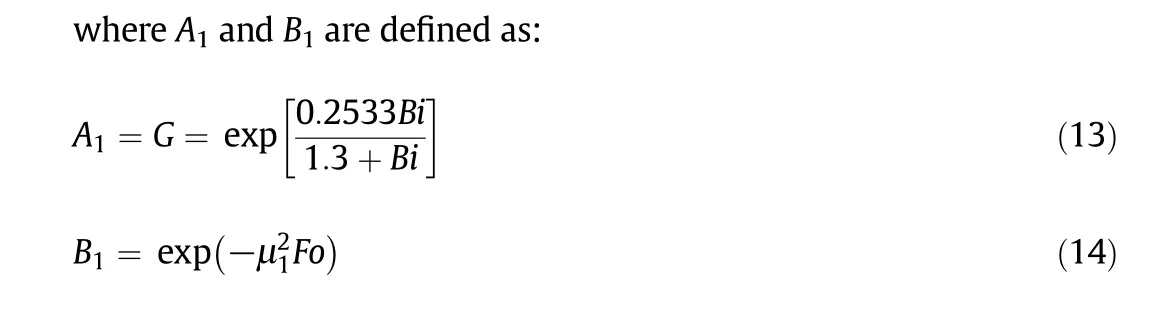
In Eq.(13),Grepresents lag factor(dimensionless)and is obtained by regressing the dimensionless values of moisture ratio and drying time in the exponential form of Eq.(15)using the least square curvefitting method[17]:

whereSrepresents the drying coefficient(s−1).

In Eq.(14),μ1is the first root of the transcendental characteristic equation and can be calculated with respect to Biot number(Bi)for in finite slab geometry by using Eq.(16)[24]:

Both Eqs.(12)and(15)are in the same form and can be equated.Therefore,by havingA1=Gand replacing Eqs.(10)and(14),the effective diffusivity for slab products is given in the following form:

To determine the mass transfer parameters based on the Dincer and Dost model,the following procedure was applied[25]:

–Using the least square curve- fitting method,the moisture ratio values and drying time were regressed in the form of Eq.(15)and the lag factor(G)and drying coefficient(S)were determined.

–The Biot number was calculated through Eq.(13).

– The value of μ1was determined from Eq.(16).

–The moisture diffusivity was calculated using Eq.(17).

–The moisture transfer coefficient was obtained from Eq.(11).

To validate the applicability of the Dincer and Dost model to describe the experimental drying curves,the dimensionless moisture ratio values were determined as follows:

–Having the effective diffusivity,Fowas calculated by using Eq.(10).

–TheB1was obtained from Eq.(14).

–Finally,by havingA1=G,the moisture ratio was determined through Eq.(12).

2.3.Activation energy(Ea)

To determine activation energy,the effective moisture diffusivity values were related with drying temperature by using simple Arrhenius equation as follows[26]:

whereDois the constant equivalent to the diffusivity at in finitely high temperature or Arrhenius constant(m2·s−1),Ris the universalgas constant(8.314 × 10−3kJ·mol−1·K−1),Tabsis the absolute temperature(K),andEais the activation energy(kJ·mol−1).

The activation energy was determined by presenting natural logarithmic of ln(D)versus1/Tabs.

2.4.Chemical analysis of the samples

Saffron samples were powdered and passed through a 40 mesh sieve.The crocins,picrocrocin,and safranal contents of the samples were analyzed following the ISO 3632 standard.Measurements of E1%of an aqueous saffron extract at 442,330 and 257 nm were carried out with a 1 cm pathway cell on a Shimadzu UV–Visible 1100 spectrophotometer.Also,moisture content was also determined according to ISO 3632[27].

2.5.Error analysis

To evaluate fitting quality of the models to the experimental data,correlation coefficient(R2),and root mean square error(RMSE)were used.These parameters are defined as[28]:

where MRexp,iis thei-th experimental moisture ratio,MRpre,iis thei-th predicted moisture ratio,MRis the average of all experimental moisture ratios,andNis the number of the observations.

3.Results and Discussion

3.1.Drying time and drying rate

Table 1 shows the average drying duration and dehydration rate values for the saffron stigmas under infrared treatment at different temperatures.It is evident that drying temperature had significant effect on drying time where the required time to reach the final moisture content at the temperatures of 60 and 110°C was about 95 and 32 min,respectively.From the table,per each 10°C increment in the drying temperature in the range of 60 °C to 100 °C caused approximately 20%reduction in the drying time and as the temperature increased from100 °C to 110 °C,the drying time decreased about 14%.The maximum(0.129 g·g−1·min−1)and the minimum(0.043 g·g−1·min−1)drying rate values were obtained for drying temperatures of 110 °C and 60 °C,respectively.The same results about drying temperature effect on the process duration and dehydration rate for various biological materials dried by using different drying methods have been reported in literature such as hot air drying of rapeseed[19]and sweet potato[29],microwave drying of spinach[30]and mint leaves[31],and infrared drying of mint leaves[32]and watermelon seeds[33].Some factors such as inherent properties,initial and final moisture content of the product,drying method and drying conditions affect drying time of the agricultural materials.At higher temperatures,the heat transfer rate between thermal source and thematerial is more which leads to faster moisture evaporation and shorter drying duration.In spite of low drying time and consumed energy,due to damaging effects on physico-chemical properties of the dried materials,high temperatures are not recommended for drying food and agricultural products.

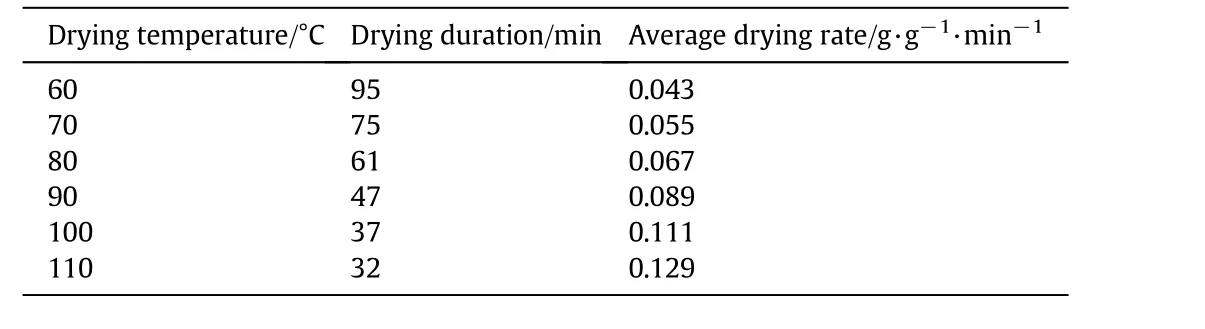
Table 1Average drying time and drying rate for infrared drying of saffron pigments at different temperatures

Variations of drying rate(g·g−1·min−1)as a function of moisture ratio at different drying temperatures are presented in Fig.1[15].The curves show that the drying process of the saffron stigmas occurred in a short accelerating rate period(warming-up)at the start followed by a falling rate period.This phenomenon has been reported for irradiated drying of high moisture content material[24,33,34].This accelerating rate period is usually negligible in the overall drying cycle,but in some cases it is significant.From Fig.1,it is clear that with an increment in drying temperature caused an increment in the warming-up period.However,this period is so limited and the main part of the drying process of the saffron stigmas took place in the falling rate period entirely.Zhenget al.[35]reported that drying of almost all biological products takes place in the falling rate period indicating that diffusion is the dominant mechanism for removing the moisture from them.In the falling-rate period,water migration from the product interior to the surface is mostly by molecular diffusion,i.e.the water flux is proportional to the moisture content gradient[35].This means that water moves from zones with higher moisture content to zones with lower values,a phenomenon explained by the second law of thermodynamics[23].

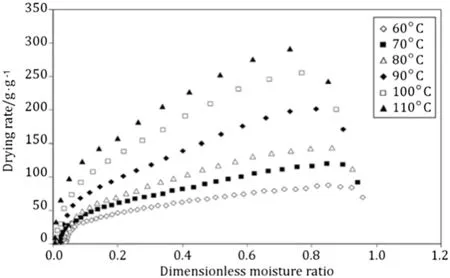
Fig.1.Variation in drying rate with moisture content for saffron stigmas during infrared drying at various temperatures[15].

3.2.Mass transfer parameters

Table 2 indicates the lag factor(G)and drying coefficient(S)obtained by using least square method and regressing the experimental moisture ratio against drying time according to Eq.(15).In addition,the values of Biot number(Bi),effective moisture diffusivity(D)and connective mass transfer coefficient(k)are presented in Table 3.

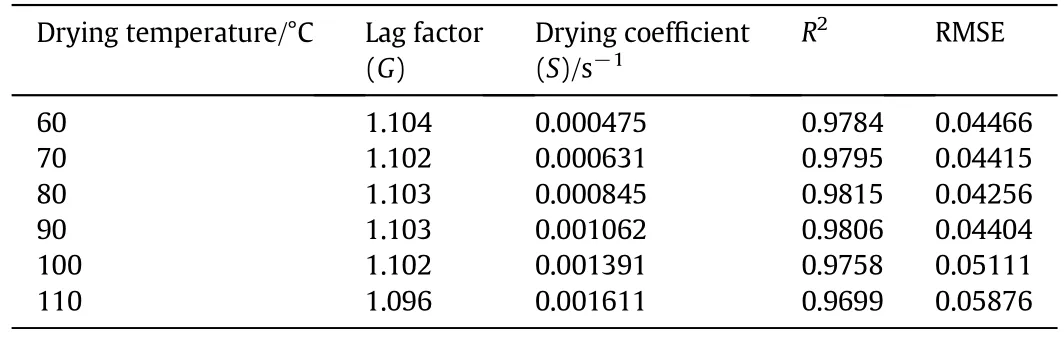
Table 2Drying coefficient(S)and lag factor(G),MR=G exp(−St),for infrared drying of saffron pigments at different temperatures

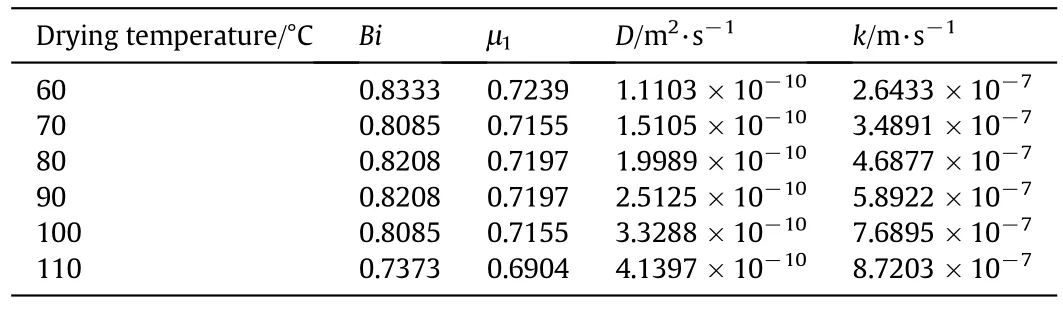
Table 3Calculated values of mass transfer parameters by Dincer and Dost model during infrared drying of saffron pigments at different temperatures

Drying coefficient shows the capability of a solid object drying per unit time and the drying process is directly related to this parameter.As the results show,the drying coefficient varies from 4.75× 10−4to 16.11× 10−4s−1.Kayaet al.[17]reported the drying coefficient for some regularly shape agricultural products such as slab carrot(0.20×10−4to 0.41 × 10−4s−1),slab pumpkin(0.16 × 10−4to 0.33 ×10−4s−1)and cylindrical carrot(0.19 × 10−4to 0.39 × 10−4s−1)dried in a convective hot air dryer at temperatures of 30,40,50 and 60 °C and constant air flow rate of 1 m·s−1[17].From the obtained results,the drying coefficient increased with increasing drying air temperature.This is due to the fact that an increment in drying temperature increases the heat and mass transfer between the heating media and solid object and consequently,leads to a higher drying capability of the object.Babaliset al.[36]reported the same results for convective hot air drying of figs in the temperature range of 55–85 °C and the air flow rate in the range of 0.5–3 m·s−1[36].

The lag factor is an indicator of magnitude of both internal and external resistances of a solid object to the heat and/or moisture transfer during drying process as a function of the Biot number.There are three cases of the Biot number:Bi＜0.1,0.1＜Bi＜100 andBi＞100.The case ofBi＜0.1 indicates that minor internal resistance and major surface resistance across the boundary layer(external resistance)to moisture transfer and moisture gradient inside the product are so small while,Bi＞100 means that internal resistance is much more than external resistance.The case of 0.1＜Bi＜100 indicates the existence of both finite internal and surface resistances and is known as the mostcommon case for the drying applications[37].The calculated Biotnumber values were in the range of0.7373–0.8333,indicating the presence of the both internal and external resistances to moisture transfer,which is consistent with reported results on literature for eggplant slices[38]and broccoli[39].

The results shown in Table 3 indicate that the moisture diffusivity values were in the range of 1.1103×10−10to 4.1397× 10−10m2·s−1which are comparable with reported values in literature for biological productse.g.,0.72 × 10−10to 3.78 × 10−10m2·s−1for watermelon seeds[33],0.62× 10−10to 3.55 × 10−10m2·s−1for orange slices[40]and 0.3982×10−10to 2.0732 × 10−10m2·s−1for mint leaves[31].In addition,the obtained moisture diffusivity values lie within the general range of 10−11–10−9m2·s−1for food materials[41].The effect of drying temperature on the moisture diffusivity can be discussed by using Fig.2.From this figure,any increment in the drying temperature leads to an increment in the diffusivity.In fact,an increase in temperature causes a decrease in water viscosity and increases the activity of water molecules.These phenomena facilitate diffusion of water molecules in object capillaries and consequently,increase the moisture diffusivity.The same results have been reported in literature by researchers for infrared drying of tomato slices[42],convective drying of sweet cherry[43]and infrared drying of wet olive husk[10].

In addition,the effect of temperature on the effective diffusivity formulated by an exponential function with a good accuracy(R2＞0.93):

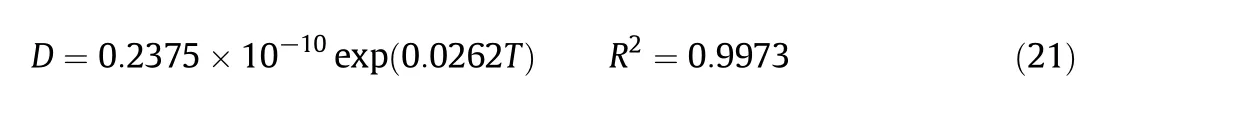
The convective mass transfer coefficient(CMTC)of the saffron stigmas was calculated on the basis of theD,BiandLvalues and by using Eq.(11).The CMTC values were obtained to be in the range of 2.6433× 10−7to 8.7203× 10−7m·s−1(Table 3).These values are comparable with the reported values for eggplant(6.478 × 10−7–2.190 × 10−6m·s−1)[38]and for whole lemons(1.660 × 10−8–1.497×10−7m·s−1)[23].In addition,the effect of drying temperature on the CMTC can be discussed by using Fig.3.The results show that the CMTC increased with drying temperature with the following function:

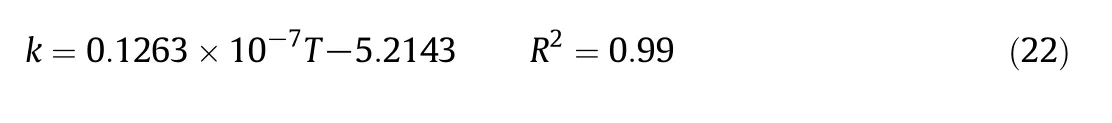
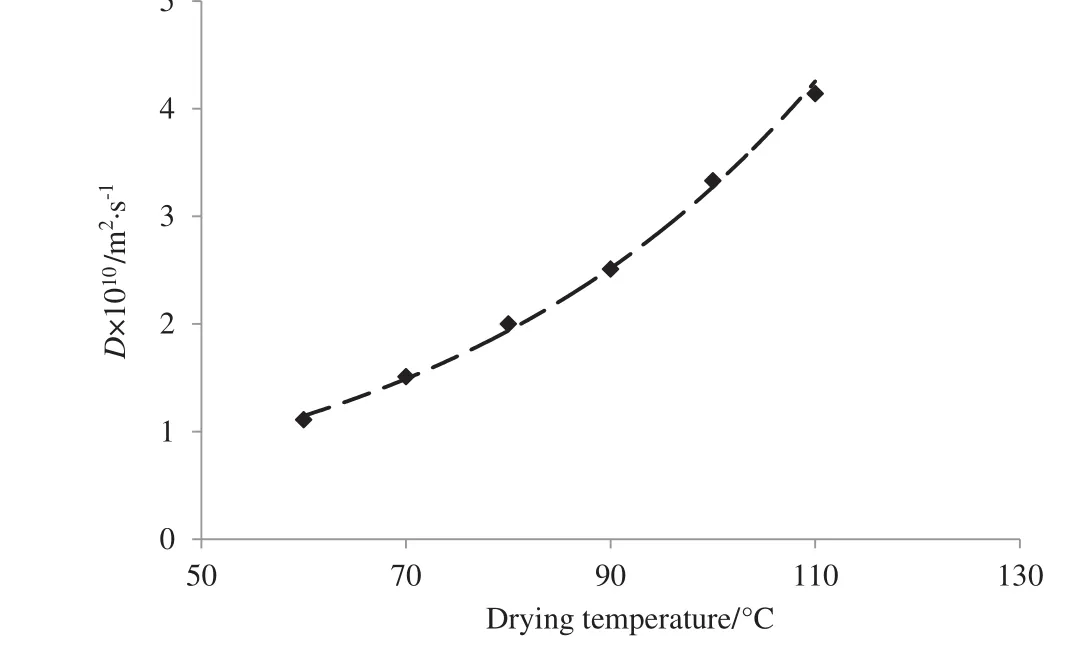
Fig.2.Effect of drying temperature on effective diffusivity of saffron stigmas.

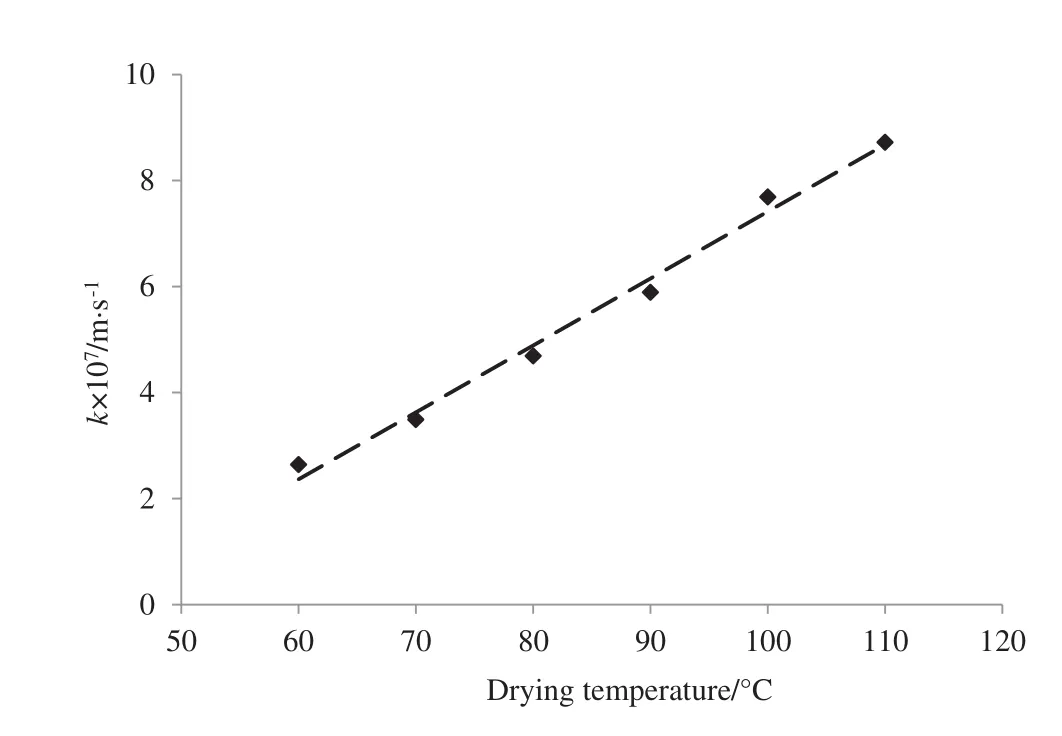
Fig.3.Effect of drying temperature on convective mass transfer coefficient of saffron stigmas.

Activation energy is defined as the measure of necessary energy needed to initiate the moisture diffusion from the internal regions of the material.The activation energy for infrared drying of saffron stigmas was determined from the simple Arrhenius equations.Fig.4 illustrates the graph of lnDagainst 1/Tabs.TheEavalue was determined to be 27.86 kJ·mol−1that is in consistent with the reported values for rapeseed(28.47 kJ·mol−1)[19],oyster mushroom(22.23 kJ·mol−1)[44]and sour variety pomegranates(23.83 kJ·mol−1)[45].

3.3.Validation of the model

To validate the applicability of the Dincer and Dost model to describe the drying curves of saffron stigmas,the dimensionless moisture ratio pro files for all drying temperatures were determined by using Eq.(12).The experimental and computed pro files of the moisture ratio variation of the samples during drying process are presented in Fig.5(a–b).From the figure,it is clear that the predicted values are in agreement with the experimental data with a reasonable accuracy for a wide range of experimental conditions.

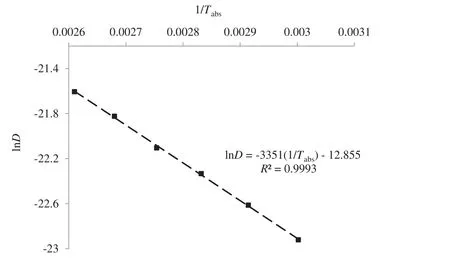
Fig.4.Arrhenius type relationship between effective moisture diffusivity and reciprocal of absolute temperature.

3.4.Chemical composition

Fig.5.Variation in experimental and predicted moisture ratios by the Dincer and Dost model with drying time for drying temperatures of 60,80 and 100°C(a),and 70,90 and 110°C(b).

Fig.6 shows the average crocin,safranal and picrocrocin contents of the samples dried at different temperatures.The crocin content increased,when dehydration temperature of the samples increased up to 90 °C but in higher temperatures(100 °C and 110 °C)the amount of crocin decreased slightly.It is clear that,the mostincrement in crocin content(approximately 37%)occurred when the drying temperature increased from 60 °C to 70 °C.In addition,as the temperature increased from 70 °C to 80 °C,and 80 °C to 90 °C,the crocin content increased about5%and 0.62%,respectively.This is probably due to thermal degradation in high temperatures orbiode gradation in low temperatures.The loss of crocin occurring in the higher temperature treatments would be the result of nonenzymatic thermal degradation,but it would appear that by keeping the high temperature in relatively short time,this loss was minimized and no enzymatic degradation would have occurred and the enzymes were denatured.Saeidiradet al.[6]reported that the crocin amount decreased with increasing of drying temperature during drying of the saffron in a convective hot air dryer at temperatures of 50,60 and 70 °C and air velocity of 0.5 and 1 m·s−1.Acaret al.[2]dried the saffron by using freeze drying and sun drying methods,and reported that freeze dried samples contained almost 40%more crocin than the sun dried samples.They attributed the low crocin content of the samples dried naturally under the sun to longer drying time that causes increased enzymatic activity and consequently,resulting in more crocin degradation[2].Also,Acaret al.[2]reported that during the freeze drying,due to extremely low water activity values(because free water is frozen)and low drying temperatures,thermal and enzymatic degradation of the stigmas of the saffron were prevented[2].

The safranal content increased with an increment in drying temperature in the range of 70–110 °C and decreased slightly when drying temperature increased from 60 °C to 70 °C.Significant increment in the safranal contents at high temperatures is most likely due to direct thermal conversion of picrocrocin at these high temperatures(100–110°C in IR drying)as opposed to the enzymatic pathway.These treatments also exhibited equal or significantly better retention of crocin pigment in comparison to the lower temperatures.This finding is in contrast with the previous work which is conducted by Carmonaet al.[5].They dried saffron by using hot air at temperatures of 70,90 and 110°C and reported that increasing drying temperature decreased safranal content of saffron.Similar results in terms of positive drying temperature effect on safranal content have been reported for hot air drying of saffron by Saeidiradet al.[6].

From Fig.6,it can be seen that the amount of picrocrocin increased from 83.1 to 93.1 as the drying temperature increased from 60°C to 110°C.This observation is in contrast with the theory postulated by some authors that the drying temperature is responsible for safranal generation from picrocrocin where safranal and picrocrocin had relatively same trends according to drying temperature and both of them increased with increasing temperature[1,46,47].Also,contrary to the illustrated bibliography,Carmonaet al.[5]observed that an increment in drying temperature caused a decrement in both safranal and picrocrocin contents of dried saffron.They attributed this phenomenon to the hypothesis that isolated picrocrocin is transformed into safranal by chemical,thermal or enzymatic treatment[5].

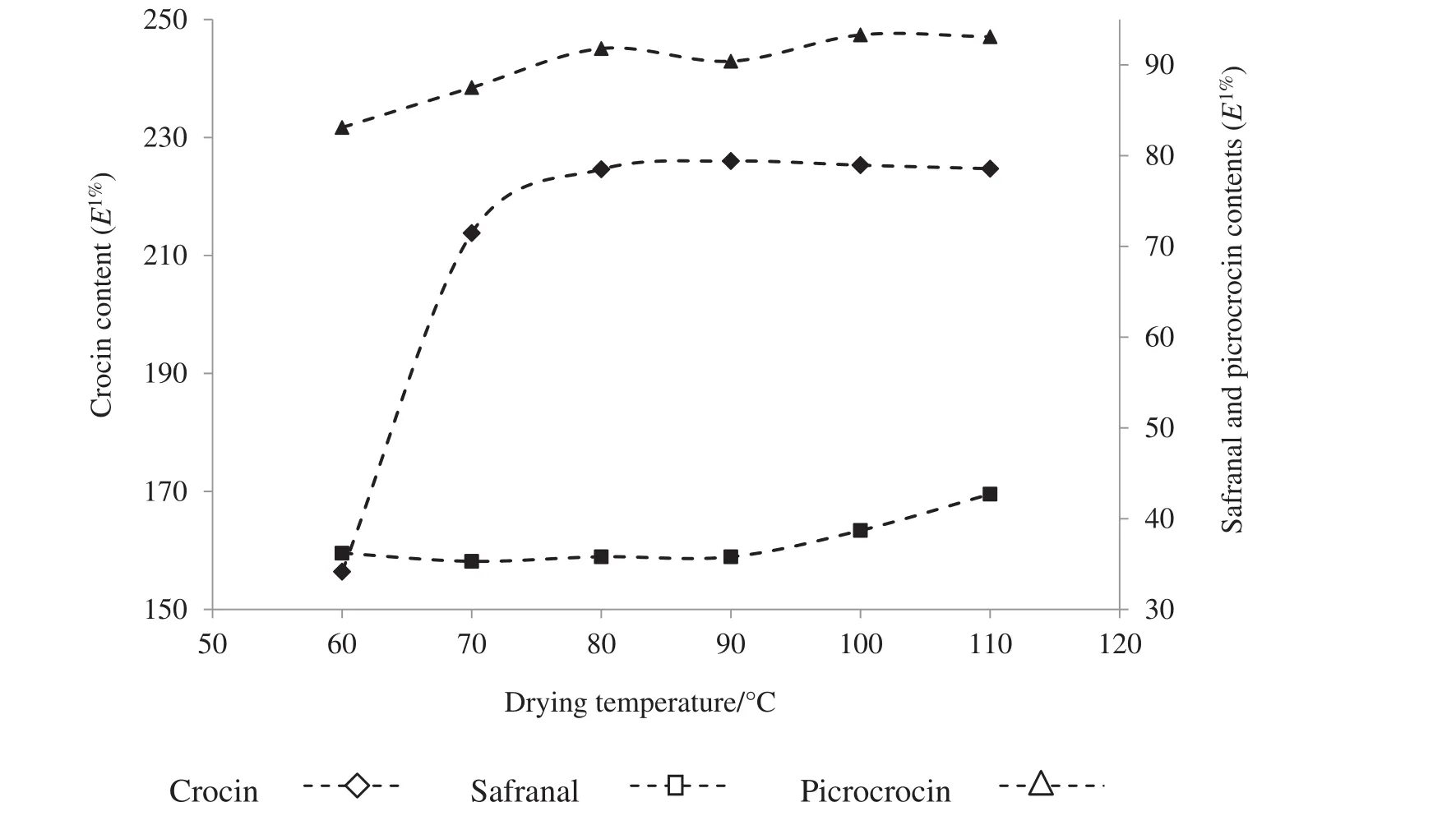
Fig.6.Effect of drying temperature on crocin,safranal and picrocrocin contents in the saffron dried under infrared treatment.

4.Conclusions

Drying kinetics,moisture transfer parameters and quality attributes of saffron stigmas during infrared treatment at different temperatures(60,70,…,110 °C)were studied.The main findings obtained from the study can be summarized as follows:

1.The dehydration process of the samples occurred in a short accelerating rate period at the start followed by a falling rate period.

2.The Biot number values indicated the existence of simultaneous finite internal and surface resistance to moisture transfer.

3.Any increase in drying temperature increased the mass transfer parameters where the effective moisture diffusivity and convective moisture transfer coefficient varied from 1.1103 × 10−10m2·s−1to 4.1397 × 10−10m2·s−1and from 2.6433 × 10−7to 8.7203 ×10−7m·s−1,respectively.

4.The maximum values of crocin and safranal were obtained in the samples treated at the highest temperature.

5.The amount of picrocrocin increased from 83.1 to 93.3 as the drying temperature increased from 60 °C to 100 °C.

[1]C.D.Kanakis,D.J.Daferera,P.A.Tarantilis,M.G.Polissiou,Qualitative determination of volatile compounds and quantitative evaluation of safranal and 4-hydroxy-2,6,6-trimethyl-1-cyclohexene-1-carboxaldehyde(HTCC)in Greek saffron,J.Agric.Food Chem.52(14)(2004)4515–4521.

[2]B.Acar,H.Sadikoglu,M.Ozkaymak,Freeze drying of saffron(Crocus sativusL.),Dry.Technol.29(14)(2011)1627.

[3]ISO 3632,Saffron(Crocus sativusL.),Part 1(Specification)and Part 2(Test Methods),International Organization for Standardization,Genève.Switzerland,1993.

[4]G.L.Alonso,R.Varón,M.R.Salinas,F.Navarro,Auto-oxidation of crocin and icrocrocin in saffron under different storage conditions,Boll.Chim.Farm.132(4)(1993)116–120.

[5]M.Carmona,A.Zalacain,J.E.Pardo,E.López,A.Alvarruiz,G.L.Alonso,In fluence of different drying and aging conditions on saffron constituents,J.Agric.Food Chem.53(10)(2005)3974–3979.

[6]M.H.Saeidirad,P.Sharayei,S.Zarifneshat,Effect of drying temperature,air velocity and flower types on dried saffron flower quality,Agric.Eng.Int.16(4)(2014)251–254.

[7]Y.Soysal,Microwave drying characteristics of parsley,Biosyst.Eng.89(2)(2004)167–173.

[8]E.Demiray,Y.Tulek,Thin-layer drying of tomato(Lycopersicum esculentum Mill.cv.Rio Grande)slices in a convective hot air dryer,Heat Mass Transf.48(5)(2012)841–847.

[9]M.Aghbashlo,H.Mobli,S.Ra fiee,A.Madadlou,A review on exergy analysis of drying processes and systems,Renew.Sustain.Energy Rev.22(2013)1–22.

[10]A.R.Celma,S.Rojas,F.Lopez-Rodríguez,Mathematical modeling of thin-layer infrared drying of wet olive husk,Chem.Eng.Process.47(9&10)(2008)1810–1818.

[11]S.Simal,A.Femenia,M.C.Garau,C.Rosselló,Use of the exponential,Page's and diffusional model to simulate the drying kinetics of kiwi fruit,J.Food Eng.66(3)(2005)323–328.

[12]C.L.Hii,C.L.Law,M.Cloke,Modeling using a new thin layer drying model and product quality of cocoa,J.Food Eng.90(2)(2009)191–198.

[13]P.N.Sarsavadia,R.L.Sawhney,D.R.Pangavhane,S.P.Singh,Drying behaviour of brined onion slices,J.Food Eng.40(3)(1999)219–226.

[14]E.K.Akpinar,Determination of suitable thin layer drying curve model for some vegetables and fruits,J.Food Eng.73(1)(2006)75–84.

[15]E.Akhondi,A.Kazemi,V.Maghsoodi,Determination of a suitable thin layer drying curve model for saffron(Crocus sativusL.)stigmas in an infrared dryer,Sci.Iran.18(6)(2011)1397–1401.

[16]B.Acar,H.Sadikoglu,I.Doymaz,Freeze-drying kinetics and diffusion modeling of saffron(Crocus sativusL.),J.Food Process.Preserv.39(2)(2015)142–149.

[17]A.Kaya,O.Aydin,I.Dincer,Comparison of experimental data with results of some drying models for regularly shaped products,Heat Mass Transf.46(5)(2010)555–562.

[18]G.P.Sharma,R.C.Verma,P.B.Pathare,Thin-layer infrared radiation drying of onion slices,J.Food Eng.67(3)(2005)361–366.

[19]L.A.Duc,J.W.Han,D.H.Keum,Thin layer drying characteristics of rapeseed(Brassica napusL.),J.Stored Prod.Res.47(1)(2011)32–38.

[20]S.M.Tasirin,I.Puspasari,A.W.Lun,P.V.Chai,W.T.Lee,Drying of kaffir lime leaves in a fluidized bed dryer with inertparticles:Kinetics and quality determination,Ind.Crop.Prod.61(2014)193–201.

[21]I.Dincer,S.Dost,An analytical model for moisture diffusion in solid objects during drying,Dry.Technol.13(1&2)(1995)425–435.

[22]I.Dincer,S.Dost,A modelling study for moisture diffusivities and moisture transfer coefficients in drying of solid objects,Int.J.Energy Res.20(6)(1996)531–539.

[23]M.Torki-Harchegani,D.Ghanbarian,M.Sadeghi,Estimation of whole lemon mass transfer parameters during hot air drying using different modelling methods,Heat Mass Transf.51(8)(2015)1121–1129.

[24]M.Sadeghi,O.Mirzabeigi Kesbi,S.A.Mireei,Mass transfer characteristics during convective,microwave and combined microwave-convective drying of lemon slices,J.Sci.Food Agric.93(3)(2013)471–478.

[25]M.Beigi,Influence of drying air parameters on mass transfer characteristics of apple slices,Heat Mass Transf.52(2016)2213–2221.

[26]T.Y.Tunde-Akintunde,Effect of pretreatments on drying characteristics and energy requirements ofplantain(Musa aab),J.Food Process.Preserv.38(4)(2014)1849–1859.

[27]V.Maghsoodi,A.Kazemi,E.Akhondi,Effect of different drying methods on saffron(Crocus sativusL.)quality,Iran.J.Chem.Chem.Eng.31(2)(2012)85–89.

[28]M.Torki-Harchegani,M.Ghasemi-Varnamkhasti,D.Ghanbarian,M.Sadeghi,M.Tohidi,Dehydration characteristics and mathematical modelling of lemon slices drying undergoing oven treatment,Heat Mass Transf.52(2)(2016)281–289.

[29]N.J.Singh,R.K.Pandey,Convective air drying characteristics of sweet potato cube(Ipomoea batatasL.),Food Bioprod.Process.90(2)(2012)317–322.

[30]I.A.Ozkan,B.Akbudak,N.Akbudak,Microwave drying characteristics of spinach,J.Food Eng.78(2)(2007)577–583.

[31]B.Özbek,G.Dadali,Thin-layer drying characteristics and modeling of mint leaves undergoing microwave treatment,J.Food Eng.83(4)(2007)541–549.

[32]C.Ertekin,N.Heybeli,Thin-layer infrared drying of mint leaves,J.Food Process.Preserv.38(4)(2014)1480–1490.

[33]I.Doymaz,Experimental study and mathematical modeling of thin-layer infrared drying of watermelon seeds,J.Food Process.Preserv.38(3)(2014)1377–1384.

[34]A.Esehaghbeygi,K.Pirnazari,M.Sadeghi,Quality assessment of electrohydrodynamic and microwave dehydrated banana slices,LWT Food Sci.Technol.55(2)(2014)565–571.

[35]D.J.Zheng,Y.Q.Cheng,H.J.Liu,L.T.Li,Investigation of EHD-enhanced water evaporation and a novel empirical model,Int.J.Food Eng.7(2)(2011),http://dx.doi.org/10.2202/1556-3758.1796.

[36]S.J.Babalis,V.G.Belessiotis,In fluence of the drying conditions on the drying constants and moisture diffusivity during the thin-layer drying of figs,J.Food Eng.65(3)(2004)449–458.

[37]I.Dincer,Moisture transfer analysis during drying of slab woods,Heat Mass Transf.34(4)(1998)317–320.

[38]X.Liu,H.Hou,J.Chen,Applicability of moisture transfer parameters estimated by correlation between Biot number and lag factor(Bi–G correlation)for convective drying of eggplant slices,Heat Mass Transf.49(11)(2013)1595–1601.

[39]V.Mrkic,M.Ukrainczyk,B.Tripalo,Applicability of moisture transferBi–Dicorrelation for convective drying of broccoli,J.Food Eng.79(2)(2007)640–646.

[40]S.Ra fiee,M.Shari fi,A.Keyhani,M.Omid,A.Jafari,S.S.Mohtasebi,H.Mobli,Modeling effective moisture diffusivity oforange slices(Thompson Cv.),Int.J.Food Prop.13(1)(2010)32–40.

[41]A.Maskan,S.Kaya,M.Makan,Hot air and sun drying of grape leather(pestil),J.Food Eng.54(1)(2002)81–88.

[42]R.Sadin,G.R.Chegini,H.Sadin,The effect of temperature and slice thickness on drying kinetics tomato in the infrared dryer,HeatMass Transf.50(4)(2014)501–507.

[43]I.Doymaz,O.Isamil,Drying characteristics of sweet cherry,Food Bioprod.Process.89(1)(2011)31–38.

[44]Y.Tulek,Drying kinetics of oyster mushroom(Pleurotus ostreatus)in a convective hot air dryer,J.Agric.Sci.Technol.13(5)(2011)655–664.

[45]S.Minaei,A.Motevali,E.Ahmadi,M.H.Azizi,Mathematical models of drying pomegranate arils in vacuum and microwave dryers,J.Agric.Sci.Technol.14(2)(2012)311–325.

[46]H.Himeno,K.Sano,Synthesis of crocin,picrocrocin and safranal by saffron stigmalike structures proliferated in vitro,Agric.Biol.Chem.51(9)(1987)2395–2400.

[47]P.Winterhalter,R.M.Straubinger,Saffron.Renewed interest in an ancient spice,Food Rev.Int.16(1)(2000)39–59.