Analogy between adsorption and sorption:An elementary mechanistic approach.I.Monolayer adsorption and sorption without solvent cluster formation

Pierre Schaetzel*,Sébastien Thomas ,Hasna Louahlia Gualous

1 Laboratoire Universitaire des Sciences Appliquées de Cherbourg,Université de Caen,IUT de Caen,Boulevard Maréchal Juin,14032 Caen cedex,France

2 Institut de chimie et procédés pour l’énergie,l’environnement et la santé,Université de Strasbourg,25 rue Becquerel,67087 Strasbourg cedex 2,France

1.Introduction

When a gas or a volatile organic solvent is absorbed by a zeolite or on activated carbon,the process is called adsorption.When a gas or an organic solvent is absorbed by a polymer,the process is called sorption.The first surprise is to see that the colonization of a solid matrix by a gas,a liquid or a vapor is denominated by two differentnames depending on the nature of the solid.It is recognized that“adsorption”is a surfacebased process while“absorption”involves the whole volume ofthe material;the term“sorption”encompasses both processes.Therefore,the sorption of gas or organic vapor on polymer generally includes surface adsorption and filling of polymervolume simultaneously.The equilibrium curves are obtained at constant temperature and are called adsorption or sorption isotherms.The theory of monolayer adsorption which is predominant at low pressure was derived by Langmuir in 1916:it is based on the classical theory of sorption and desorption[1].Sorption and desorption are represented by a simple chemical equilibrium equation.The result of this very simple and rigorous theory is the Langmuir equation.For polymers the theory derived independently by Huggins and Flory is based on the calculation of the entropy and of the enthalpy of mixing macromolecules and solvent from the point of view of a statistical thermodynamics theory in which the solvent particles and macromolecules are assigned to positions in an imaginary lattice[2-5].The development of these calculations results in the Flory-Huggins equation.

The demonstration and the formalism of the Langmuir equation and of the Flory-Huggins equation are extremely different which can justify a very different scientific approach of adsorption and sorption.This is well accepted as the shapes of the isotherms are also extremely different.The sorption isotherms obtained with a sorption micro balance represent the variation of the volume fraction of the solvent in the polymer vs the activity of the solvent:the experimental curves are generally convex.The adsorption isotherms representing the variation of molality of the solute adsorbed on the solid matrix vs the activity of the solventcan be obtained by the same experimental device.

In both cases(sorption and adsorption),the phenomena involved seem to be rather similar:the colonization of a solid solvent by a solute.The question is:why are the scientific approaches so different?Two similar scientific phenomena should be explained by two similar equations or even better by the same equation.This paper is a trial of a very naïve theory of adsorption and sorption which will be qualified by the community as a “mechanistic theory”.The sole ambition of our approach is to examine if experimental sorption and adsorption isotherms are described by a simple colonization law of the free sites existing in the polymer matrix or on the surface of the pores of the adsorbent.We will see that the sole difference between both processes(adsorption and sorption)is that adsorption is the filling process of the pore walls and sorption is the filling process of the polymer volume.This paper only describes the model with a simple adsorption or sorption mechanism when one sorption or adsorption site sorbs or adsorbs one and only one solute molecule.More complex processes with two or more adsorption/sorption modes,like multilayer adsorption or“dual mode”type sorption,or sorption generating solvent clusters in the polymer matrix will be treated in a next paper[6-11].

2.Classical Adsorption and Sorption Theories

2.1.The Langmuir theory of adsorption

To give a better perception of the Langmuir theory of adsorption we have to understand the original paper which is a general re flection on equilibrium and non-equilibrium[1].The idea of Irving Langmuir is that there is a competition between the rate of condensation and the rate of evaporation on the surface of the material.The rate at which the gas molecules come into contact with the adsorbent surface is given by the kinetics theory of gases:

flux of gas molecules arriving on the surface of the adsorbent(mol·m-2·s-1)

M molecular weight of the gas

R gas constant(J·mol-1·K-1)

T absolute temperature(K)

P pressure(Pa)

S exchange area of the adsorbent(m2)

For Langmuir the chocks between the gas molecules and the adsorbentsurface are largely inelastic:large majority ofthe molecules arriving condense on the solid surface.

The rate of condensation per unit area of solid˙NCis

αis the efficiency of condensation which is very close to unity and(1-θ)represents the fraction of surface which is bare.

The rate of evaporation is equalto˙Nvθwhereθrepresents the fraction of occupied surface and˙Nvthe mean flux of evaporation.At equilibrium the condensation flux and the evaporation flux are equal:

Langmuir obtained:

is constant andis proportional to P.One defines k′as:

The classical Langmuir adsorption equilibrium equation writes:

In this equation k′is always positive.n and n′0are respectively the number of moles and the maximum number of moles(at in finite pressure)adsorbed in the solid.

2.2.The Jovanović theory of adsorption

In 1969 Jovanović has demonstrated,using new kinetics arguments,a monolayer and a multilayer adsorption law[2].The demonstration of Jovanović uses the main hypotheses than those assumed by Langmuir with a fundamental difference concerning the rate of condensation.The author writes that the Langmuir model is not correct as the surface available to adsorption is not proportional to(1-θ)in Eq.(2)but a little higher due to the evaporation of adsorbed molecules,while the other term of the equation is unchanged.The main difference between the Langmuir model and the Jovanović model is that Langmuir neglects the collisions between the bulk and the adsorbed molecules.The kinetic treatment of adsorption by Jovanović is rather complicated as mentioned by Jaroniec[3].The result is the Jovanović equation of adsorption:n=n0(1-e-KP).

Jaroniec[3]uses the mechanical statistics theory to demonstrate rigorously the Jovanović equation:he writes that in the language of statistical mechanics,considerations of Jovanović take into account the mechanical contact between adsorbed and bulk phase.Thus,while the classical Langmuir model may be described by means of the grand canonical ensemble the model of Jovanović can be described by means of the generalized ensemble,taking account of mechanical contacts with surroundings[3].We will see that an elementary mechanistic model will give a third demonstration of the Jovanović equation and will be generalized to an elementary mechanistic sorption model of vapors and gases in polymers.

2.3.The Flory-Huggins theory of sorption

Here,we give a brief description of the lattice model of mixing demonstrated independently by Huggins and Flory[2-5].The details of the demonstration can be found in the original articles.We insist only here on the principal hypotheses used in the model and on the significance of the constants and parameters appearing in the demonstration.

The Flory-Huggins theory uses a lattice model to arrange the polymer chains and solvent molecules.The polymer-solvent solution is arbitrarily divided into a set of N0cells:each cell can be occupied by either one segment of the polymer or one solvent molecule.One polymer chain contains N segments.The polymer segments are interchangeable with the solvent molecules which means that they have an identical molar volume[3].To get the entropy of mixing,Flory calculates the number of configurations when polymer macromolecules are added to a solvent.The Boltzmann equation and the mathematical Stirling approximation yield the entropy of mixing for one site:

ϕ is the volume fraction occupied by the solvent and(1-ϕ)is the volume fraction occupied by the polymer,kBis the Boltzmann constant.

The next step of Flory's demonstration is the computation of the enthalpy of mixing for one site.When a polymeric solute is added to a solvent,an enthalpy change occurs because solvent-solvent and solute-solute interactions are replaced by solvent-solute interactions.According to the lattice theory,such interactions may be representedby the numbers and types of nearest neighbors in the lattice,a nearestneighbor interaction may be defined as a lattice contact,so there will be three types of such contacts:

·Polymer segment-polymer segment

·Solvent molecule-solvent molecule

·Polymer segment-solvent molecule.

By analogy to the classical theory of mixing the result for the enthalpy of mixing is

T is the absolute temperature,andχis the Flory-Huggins interaction parameter which can be positive,negative or nil.The free energy of mixing is thus given by:

The partial differentiation of the free energy of mixing leads to the chemical potential of the solvent in the polymer-solvent solution and thus to the activity of the solvent:

This is the Flory-Huggins equation.For long polymer chains r′tends to zero and one obtains the “simplified”Flory-Huggins equation:

Both equations can be fitted to experimental sorption isotherms but the complete Flory-Huggins equation has to be privileged as it corresponds to the rigorous statistical thermodynamics demonstration of Flory[2,3].When r′is found negative,it means that for the given system the theory cannot be applied even if the determination coefficient is high.Another condition is that r′which is defined by Flory as the inverse of the number of segments in the polymer chain must be lower than unity.The limit is 1 which corresponds to a polymer chain containing only one segment which volume is then the same as that one of the solvent molecule.The condition for r′is:

This condition is rarely analyzed when one fits experimental data to Flory-Huggins equation despite it is one of the key hypotheses in the demonstration.Many papers never consider the complete equation but only the equation where r′is neglected.

3.An Elementary Mechanistic Theory of Adsorption and Sorption

3.1.Adsorption theory

In the solid matrix of the adsorbent we assume that the adsorption sites are uniformly distributed on the walls of the pores(Fig.1).

Each adsorption site can only adsorb one gas(or solvent)molecule.In other terms,when one site is already occupied by one gas or one solvent molecule,the solute can only colonize one free remaining adsorption site.We assume that the differential increase of the number of solute molecules adsorbed(d n)is proportional

·to the differential increase of activity of the solute(d a)

·and to the surface concentration of the free sites

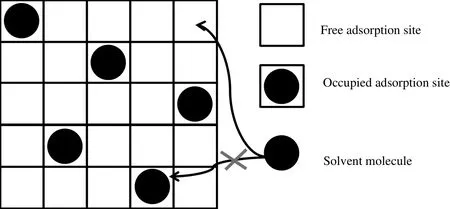
Fig.1.Principle of the elementary unified adsorption/sorption theory.The adsorption or the sorption of a solvent molecule on an occupied site is not allowed.Only free adsorption sites can be occupied by the solvent molecule.

n0is the total number of adsorption sites on the surface of the pores in the solid adsorbent for a given solute and a given temperature,n is the number of sites already occupied.The differential adsorption equation writes:

k is the affinity coefficient between the free adsorption sites and the solute at a given temperature,S is the area of the pores when the pore walls are occupied by n solute molecules and S0is the area of the pores when the pore walls are uncovered by any solute molecules.

For a rigid adsorbent one can assume that the total pore area is constant and equal to that existing before the beginning of the adsorption process S0.In other terms,we assume that the adsorption process does not change the area of the pores:

With this assumption Eq.(14)becomes:

To obtain the adsorption equation Eq.(16)has to be integrated.

The result is:

The fractional coverage θ of the adsorption sites by the gas is given by:

This is the adsorption equation in the filling of free sites theory in the one adsorbed molecule for one free site hypothesis.At moderate pressure the activity of the solute(gas or vapor)is the ratio of the pressure to the vapor pressure of the solute at the temperature of the adsorption experiment:

One can give the expression in function of the pressure:

The adsorption relationship writes:

with:

K is the practical affinity coefficient.The simple demonstration with elementary butacceptable hypotheses leads to the equation of sorption of Jovanović.The hypotheses of the model are validated as Jovanović and Jaroniec arrive to the same result with more rigorous demonstrations based on kinetic and on statistical mechanics.This allows us to generalize our elementary model to vapor or gas sorption in polymers.

The fractional coverage θ of the adsorption sites by the gas is given by:

When ϕ tends to zero one obtains the following Henry equation:

We have represented on Fig.2 typical adsorption isotherms obtained by Eq.(24)with variable K coefficients.

Fig.2.Simulation of the adsorption isotherms with Eq.(24).Numbers on the curves correspond to the K value(MPa-1)used to generate the curves.

3.2.Sorption theory

We assume that sorption sites are uniformly distributed in the dry volume of the polymer.The volume of the dry polymer is divided into identical elementary solid particles,each containing a single adsorption site.We realize an ideal partition of the dry polymer.The particles have the same volume and the same shape.One solvent molecule can only be associated with one of these elementary polymer particles(Fig.1).When the polymer swells,the volume and the shape of these elementary particles are unchanged.

The concentration of these elementary particles is characterized by their molarity:this is the sole difference between the sorption and the adsorption theory.In the elementary adsorption theory the adsorption sites are localized on the pore surface:the concentration is defined by the number of adsorption sites per unit area of the pore surface.While in the elementary sorption theory the adsorption sites are uniformly dispersed in the volume of the polymer:their concentration is expressed in number of sites(equal to the number of elementary polymer particles)per unit volume of the swollen polymer i.e.in molarity.We assume that the differential increase of the number of sorbed solute molecules d n is proportional to the elementary increase of the activity d a and to the molarity of the free sorptionthe molarity of the solvent free elementary polymer particles.The coefficient k is the affinity coefficient between the sorption sites and the solute,v0is the volume of the dry polymer and v the volume ofthe swelled polymer.

At evanescents welling(v≈v0)Eq.(26)forsorption and Eq.(16)for adsorption are identical.This observation justifies clearly that the affinity coefficient for sorption and adsorption are of the same nature:the same symbol k is used in both processes to characterize the affinity of the solvent for the sorption or adsorption sites.It is clear to us that adsorption and sorption are similar processes with the same mode of colonization of the free sorption or adsorption sites.The sole difference is that sorption is a volumetric filling process and that adsorption is a surface filling process.

As the volume and the shape of the elementary polymer particles do not change during the sorption process the affinity coefficient is independent of swelling,depending only on the polymer-solvent system and on temperature.The number of polymer particle changes with temperature as the activation of the sorption sites is temperature dependent.

The molar volume of the sorption polymer particles is V0and the number of particles in the polymer sample is n0.The volume of the dry polymer v0is given by:

Assuming additivity of the volumes,we obtain the volume v of the swollen polymer:

V is the molar volume of the solvent and n the moles of solute sorbed by the polymer.The volume fraction ϕ occupied by the solvent in the polymer is given by

Eqs.(27)to(29)allow calculating n in function of ϕ:

The differential sorption equation(Eq.(26))can then be expressed with the variable ϕ:

r is the ratio between the molar volume of the solute V and the molar volume V0of the elementary polymer particles containing one sorption site:

We can notice that the ratios r and r′appearing in this sorption model and in the lattice chain model of Huggins and Flory have different significations.r′represents the ratio between the volume of one solvent molecule(or a polymer segment)and the volume of one polymer chain.The polymer chain is composed by N segments having the same volume as the solvent molecule.As they have strictly the same volume,each solvent molecule or each segment can be placed in an elementary cell.The maximum for the r′ratio is thus 1(the polymer chain is composed by one unique segment),the minimum is zero(the polymer chain is composed by an in finity of segments).The definition of the r ratio is quite different(Eq.(32)):its value is of course positive but it can be lower or higher than unity.Nevertheless we expect that its value is rather low:a low r value means that there are a small number of adsorption sites in the polymer.

We have to integrate the following expression:

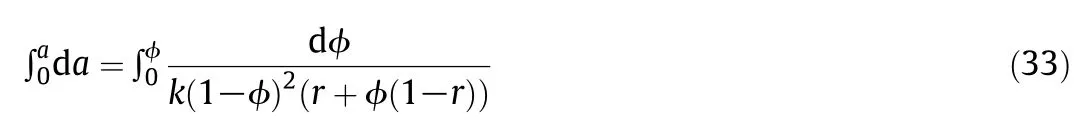
The integrated sorption equation is:

This is the result of the equilibrium sorption equation obtained with the unified elementary sorption theory.When ϕ tends to zero one obtains the following Henry equation:

Using Eq.(30)when ϕ tends to zero

and Eq.(30)writes

This is the same limiting linear equation as the one obtained for adsorption.

On Fig.3a,we have represented typical isotherms given by Eq.(34)for a fixed r ratio(r=0.02)with stepwise changes of the affinity coefficient k from 1 to 8.As expected,sorption grows dramatically with k:for a saturated solvent(a=1),the volume fraction of the sorbed species in the polymer is multiplied by 25 growing from 0.03(k=1)to 0.75(k=8).

For the lowest affinity coefficient(k=1),as the volume fraction of the solvent in the polymer is low,the sorption isotherms become nearby linear which is the classical Henry law.For relatively low k ranging from 2 to 4 we observe on Fig.3a the classical shape described by the Flory-Huggins theory.For higher affinity coefficients(5 to 8)the shape of the curves is of a “dual mode”type which qualification is improper in our sorption equation,as it describes the filling process of the polymer by the sorbed molecules through a unique mode:one solvent molecule colonizes selectively one free sorption site.

We note that the activity of the solvent is the sum of two terms:

We call the first term aHof this sum Henry activity as:

Fig.3.a.Simulated sorption isotherms calculated by Eq.(34)atvariable affinity coefficient k.The r ratio has been put to 0.02.b.Ratio of the “adsorption activity”a A(Eq.(40))to the activity a(Eq.(34))vs the volume fraction of the solvent in the polymer for the affinity coefficient k set to 3 with variable r ratios.

We callthe second term aAadsorption activity as its expression has a formalism which resembles to that of the new equation for adsorption(Eq.(19)):

To evaluate the importance of the “adsorption activity”on the total activity we have simulated on Fig.3b the ratio between aAand the total activity.The ration is independent of the affinity coefficient and the r ratio is stepwise changed(Fig.3b).

At low r(0.01 to 0.03)the solvent in the polymer(lower than 0.2),the“adsorption activity”accounts formore than 90%in the“total”activity and for more than 70%of all computed points.We can thus define an approximate adsorption law which neglects the “adsorption activity”:it is valid for low r ratios which means for adsorbents with low concentration in adsorption sites.This simplified or approximate sorption law writes:

It can be reversed to obtain the volume fraction at equilibrium vs the activity of the solvent(that is not possible with the full sorption equation):

To examine if the new adsorption and sorption relationships are valid,we will now try to fit experimental isotherms into the new equations and compare the quality of the non-linear least square calculation to that of the classical models.

4.Test of the Elementary Unified Adsorption and Sorption Theory

4.1.Test of the elementary adsorption theory

4.1.1.Adsorption on activated carbon

Our elementary adsorption theory,in this first paper,only describes the simple process where one adsorbent molecule will be associated with a single adsorption site:Fig.2 clearly shows that Eq.(24)only generates adsorption isotherms of the Lang muirtype.To test the adsorption equation we have searched the literature in relatively recent papers in which the authors obtained isotherms with this characteristic type I shape and where data is given in extensive tables with experimental points distributed regularly on the totality of the pressure range.The two most used adsorbents(i.e.activated carbon and zeolites)are analyzed to examine if the mechanism of adsorption on both solids is well described by the elementary unified theory.

Loh et al.have measured the adsorption of methane on activated carbon at high pressure(from 0 to 2.5 MPa)for eight temperatures(ranging from 5 to 75°C)[12].This paper is particularly interesting as the authors publish the data for eight temperatures and this will give us the possibility to test empirical temperature dependency laws for n0and K.On Fig.4a and Table 1,we have compared the least fit square of the experimental data of Loh et al.to the Langmuir equation(Eq.(6))and to the elementary adsorption equation(Eq.(24)):both equations give a good description of the adsorption phenomenon.But we can observe on Table 1,that the coefficient of determination and the χ2value indicates a better representation of the adsorption by the Langmuirmodel,essentially atlow temperature.Athigher temperature,both equations are equivalent with a small advantage for the Langmuir model.

On Fig.4b,we have represented the variations of ln n0and ln K with the inverse of the absolute temperature(1/T).Both curves are straight lines.The temperature variations of the parameters of the adsorption model are thus represented as expected by pseudo-Arrhenius equations:

We have found for Eq.(43):n=2.44ewith a determination co-

0efficient equal to 0.990.For Eq.(44)the result is:K=0.0206e.The determination coefficient is 0.988.All numerical parameters are given in SI units.

Wu et al.have measured the adsorption of N2and H2on activated carbon at three different temperatures[13].Both models,Langmuir(Eq.(6))and the elementary adsorption theory(Eq.(24))correctly fit the experimental isotherms with a small advantage in the case of N2for the classical Langmuir model with slightly higher determination coefficients(Table 1).A better correlation is obtained for the elementary unified model for H2for which the isotherms are nearby linear.

Fig.4.a.Adsorption experimental data of CH4 on ACF(A20)activated carbon:solid lines are from Eq.(22)and broken lines are from the Langmuir equation(Eq.(6))[12].b.Variation of the logarithm of the parameters K and n0 of Eq.(22)vs the inverse of the absolute temperature.

4.1.2.Adsorption on zeolite 5A

Adsorption on zeolites takes more and more importance in adsorption and catalytic processes.In 2005,Nam et al.published high pressure adsorption equilibrium data using a static volumetric method[14].CH4,C2H6,C2H4,N2,and H2were adsorbed on zeolite 5A from 0 to 1.8 MPa at three temperatures:293.15 K,303.15 K and 313.15 K(Fig.4 and Table 2).The efficiency of the fitting of the experimental data to Eq.(24)to the Langmuir equation(Eq.(6))is clearly average for C2H6and C2H4with poor determination coefficients and large chi-square values(Table 2).It is nevertheless evident on Fig.4 that the Langmuir(Eq.(6))equation is poorly adapted to represent the adsorption of ethane and ethylene on a zeolite 5A,while the simple unified adsorption theory equation(Eq.(22))gives an acceptable representation of the isotherms for both components.For methane and N2both theories are able to represent the isotherms with a better precision for the elementary adsorption theory(Eq.(24)),while for hydrogen both equations yield the same quality of curve fitting.We observe on Table 2 that for nitrogen,methane and ethylene the concentration of the adsorption sites n0is approximately constant

Table 1 Results of fitting the experimental adsorption isotherms of CH4 on ACF A20 activated carbon,N2 and H2 on activated carbon JX101 to the adsorption equation(Eq.(24))and to the Langmuir equation(Eq.(6))[12,13].P holds for the pressure range of the experimental adsorption isotherms

Table 2 Parameters obtained by curve fitting the experimental adsorption isotherms on zeolite 5A to Eq.(22)and to the Langmuir equation(Eq.(6))[14]

with only a small decrease in temperature.For these three compounds its mean value is:

The difference in the adsorption capacity by the zeolite 5A of these three compounds is the result of the value of the affinity coefficient K which is about 1 MPa-1for nitrogen,3 MPa-1for methane and 8 MPa-1for ethylene.The hypothesis of the same type of adsorption sites for these three solutes is confirmed by a similar behavior when analyzing the isotherms with the Langmuir equation.

The behavior of ethane is slightly different with a molality of the free adsorption sites n0of about 3 mol·kg-1and a high affinity coefficient varying from 12.2 to 7.5 which traduces the high affinity of ethane for the zeolite 5A.Hydrogen only has a weak affinity for the tested zeolite with small affinity coefficients and a small molality of the adsorption sites.Contrary to all other components,the affinity coefficient K increases with temperature:this fact probably denotes another mode of sorption.The isotherms are quasi-linear.

On Fig.5 we have represented the gas-sorbent affinity coefficient K as defined by Eq.(23)vs the Langmuir k′coefficient(Eq.(6))for both sorbents(activated carbon and zeolite 5A)-gas isotherms analyzed.K is proportional to k′(Fig.6a):

On Fig.6b we observe that the number of moles of adsorption sites per unit mass of sorbent n0(Eq.(22))is proportional to the maximum concentration of adsorbent at in finite pressure n′0as defined in Eq.(6):

Fig.5.Curve fitting of experimental isotherms of H2,N2,CH4,C2H4,and C2H6 on zeolite 5A at 303.15 K to the elementary adsorption theory Eq.(22)(full lines)and to Langmuir equation(broken lines)[14].

Fig.6.a.Affinity coefficient K(Eq.(22))of the elementary unified adsorption theory vs the Langmuir coefficient k′(Eq.(6))for all isotherms analyzed.b.Concentration of total number of adsorption sites n0(Eq.(22))vs the maximum concentration of adsorbed gas molecules n′0(Langmuir equation:Eq.(6))for all isotherms analyzed[12-14].

Both observations lead to a common conclusion:the two theories(the unified adsorption theory and the Langmuir theory)are the same,and with two common hypotheses:it is assumed that the sorbent surface is covered uniformly by adsorption sites and that an occupied adsorption site is not allowed to adsorb a further solute molecule.

4.2.Test of the elementary unified theory for sorption in polymers

Now,we have to compare the efficiency of non-linear curve fittings of experimental isotherms to the elementary unified theory of sorption and the classical Flory-Huggins theory.We have chosen 11 isotherms to analyze and have confronted the experimental data to four equations(Table 3):

·The sorption equation which is the result of the elementary unified theory(Eq.(34))

·The simplified sorption equation obtained by neglecting the “Henry activity term”in Eq.(34)(Eq.(40))

·The classical mechanical statistics equation of Flory-Huggins(Eq.(10))

·The simplified Flory-Huggins equation(Eq.(12))obtained by neglecting in Eq.(10)the ratio r′between the molar volume of the solvent and of the polymer chain.

The 11 polymer/solvent systems are chosen to cover most types of sorption encountered in function of the polarity of each compounds(Table 3):polar polymers can sorb non-polar or polar solvents and non-polar polymers can also sorb both types of solvents.

We see that the equation obtained with the elementary unified theory(Eq.(34))correctly fits all 11 isotherms analyzed.As expected,the ratio r between the solvent molar volume V and the molar volume of the elementary polymer chain containing one single adsorption site V0is always positive and small:its value varies from 0.007 to less than 0.09.The r coefficient and the affinity coefficient k can be considered to be constant for a given solvent-polymer system.The value of both coefficients varies slightly with temperature.One of the consequences of the statistical analysis of the experimental isotherms is that the model is coherent with the hypotheses affected during the demonstration.The most important one is that one solvent molecule can only “colonize”one single adsorbent site:it seems that,for the 11 isotherms analyzed here,with F-H like shapes,the sorption process occurs without the formation of solvent clusters in the polymer matrix.In other terms,the simple sorption process has the same mechanism of filling of the free sites than the adsorption process(with type I isotherm shapes).The difference,as pointed out earlier,is that for adsorption,the adsorption sites are distributed regularly on the surface of the pores while,for sorption,the sorption sites are distributed regularly in the volume of the polymer matrix.In the latter case the volume of the material varies during the sorption process while in the adsorption process the volume of the material remains constant.

The“simplified”sorption equation(Eq.(40))also gives positive and low r ratios with an equivalent curve fitting efficiency(Table 3)and relatively close coefficients in comparison with those obtained with Eq.(34).This equation is too a two parameter equation(r′and K)and is valid for low r ratios:its advantage is to be inverted to allow the explicit expression of the volume fraction of the sorbed molecule vs the activity of the vapor.Butone has to notice that the rigorous equation of our model is Eq.(34),the exact equation,and that Eq.(40),the“simplified”equation has been defined only to perform further calculations(i.e.diffusion):affinity coefficients and the r ratios are close to what is obtained with the “exact”adsorption equation.

On the contrary,the ratio r′defined in the Flory-Huggins theory(Eq.(10))as the ratio between the molar volume of the solvent and the molar volume of the polymer segment which value should be comprised between 0 and 1 is equal to 2.43 for the couple polypropylene/diethyl ketone(system 1),1.53,1.41,and 1.35 for the couple PVAc/methanol at the three temperatures investigated(systems 3,4,5)and 1.91 for the couple PVA/water(system 9).Its value is even relatively highly negative for the polar/polar couple PVP/water(system 10)and also negative(-0.495)for the non-polar/non-polar couple PS/benzene(system 11)which is more surprising as the Flory-Huggins theory is in principle adapted for such types of systems.This theory works well for the PVAc/toluene(systems 7,8,9)system,where the r′ratio is slightly positive or slightly negative.In this case where a non-polar solvent is sorbed by a non-polar polymer the exact F-H(Eq.(10))and the simplified F-H equation(Eq.(12))give approximately the same interaction parameter with high determination coefficients and relatively low chisquare values.Even for this PVAc/toluene system the new equation developed in this paper(Eq.(34))is as efficient as the F-H equation.

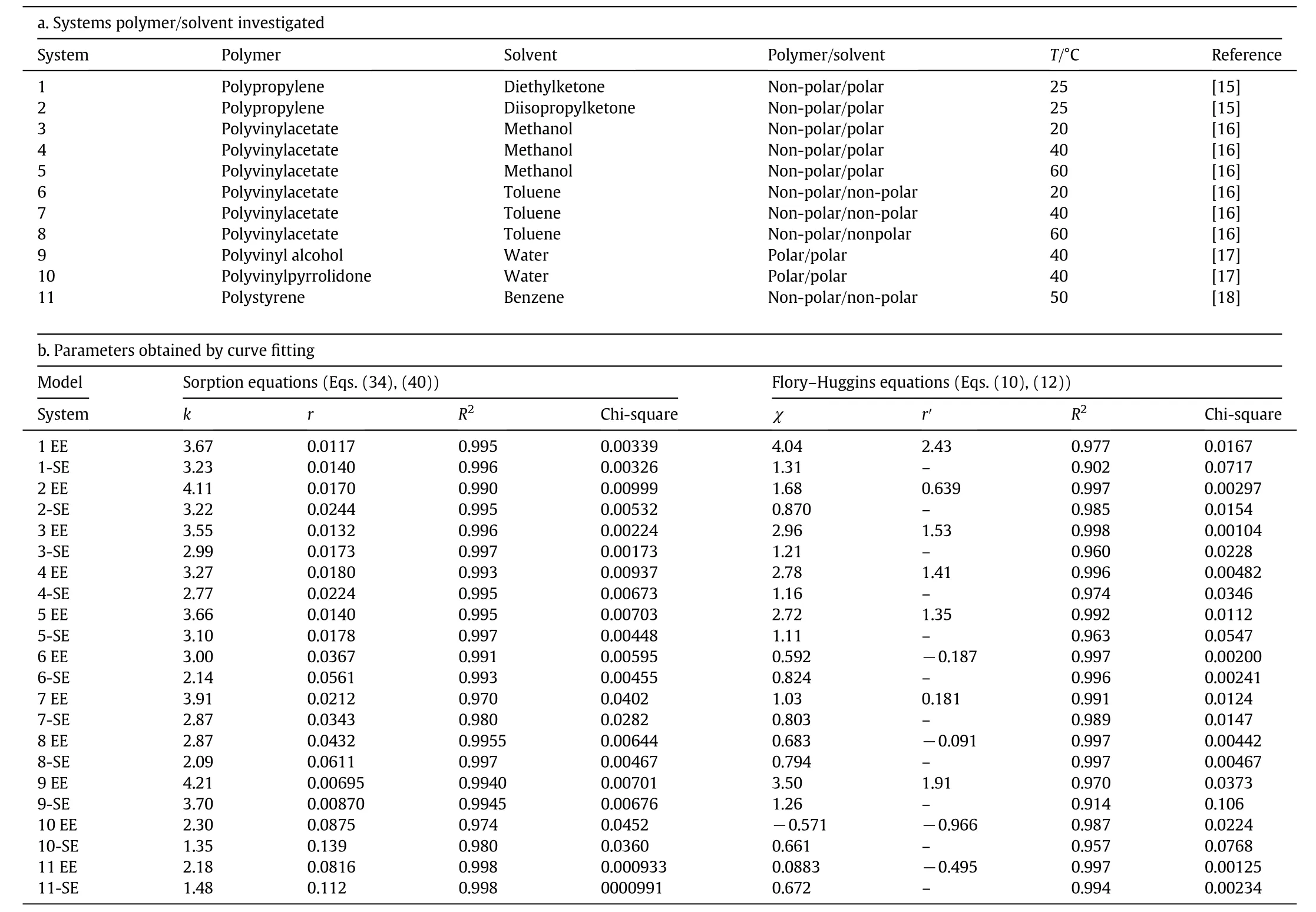
Table 3 Comparison of the parameters obtained by curve fitting experimental isotherms to the elementary unified adsorption theory equation and to the Flory-Huggins equation.EE and SE hold respectively for exact(Eqs.(34),(10))and simplified equations(Eqs.(40),(12))

Both new sorption equations(Eqs.(34)and(40)) fit correctly,even at low activities the water/PVA isotherm(system 10)where two highly polar compounds are associated:Table 3 and Fig.7a show the equal good fitofthis isothermto Eqs.(34)and(40)and the average result obtained with the full(Eq.(10))and simplified F-H(Eq.(12))equations.The r′ratio is found to be 1.91 for this system which clearly violates the hypothesis assumed in the Huggins-Flory demonstration.

When only statistical and visual(Table 3 and Fig.7b)arguments are used,the fitting efficiency ofthe PVAc/methanolisotherm(systems 3,4,5)to both sorption equations(Eqs.(10)and(34))seems to be equivalent:but the r′ratios are clearly higher than unity.This violates one of the key hypotheses in the demonstration of Flory,i.e.the equality of the molar volumes of the elementary polymer segment and the solvent molecule.The F-H equation is not appropriate to describe the behavior of this system for the 3 temperatures investigated.This observation is reinforced by the fact that the statistical criteria(determination coefficient and chi-square)are average for the simplified F-H equation(Eq.(12)).

5.Conclusions

The goal of this paper was to analyze the mechanism of the colonization of a solid(sorbent or polymer).We have proposed an elementary and common mechanism for the filling of the solid in both cases.In the case of adsorption,the adsorptions sites are distributed uniformly on the pore walls and they are characterized by a surface concentration.In the case of sorption the sorption sites are distributed uniformly in the volume of the polymer and are characterized by the concentration by unit volume of the total polymer-solvent mixture.We have performed an ideal partition of the dry polymerin elementary equal functional species,each containing one adsorption site and neighboring polymer chains:when the polymer swells the volume and the shape of these elementary polymer species are unchanged.

The filling law of the solids by the solute is identical for adsorption and sorption:the differentialincrease of the number of solute molecules is proportional to the differential increase of the activity of the solute and to the concentration of free sites i.e.of adsorption or sorption sites which are notyet colonized by one solute molecule.We call the proportionality constant the affinity constant.This first paper only describes the simple case where one solvent molecule is associated with a single site.The tests of this elementary theory on experimental published isotherms are satisfactory for adsorption and sorption.

An important consequence of the elementary sorption theory is that for the tested couples of polymer-solvent vapor,the absence of solvent clusters in the polymer matrix is evident,as the unified elementary theory is based on the assumption of the association of one sorption site with a single solvent molecule.This is the case for polar/polar systems but also for non-polar/non-polar systems.

This article is the first step in ouranalysis by simple arguments of the adsorption/sorption processes.The methodology will be generalized to more complicated processes with two or more adsorption/sorption modes.

Fig.7.Curve fit of experimental isotherms to the exact(Eq.(34))and simplified(Eq.(40))equations to the elementary unified sorption theory and to the exactand simplified Flory-Huggins equations.a.PVA/water at 40 °C[17].b.PVAc/methanol at 60 °C[16].

[1]I.Langmuir,The constitution and fundamental properties of solids and liquids.Part I.Solids,J.Am.Chem.Soc.38(1916)2221-2295.

[2]D.S.Jovanović,Physical adsorption of gases I:Isotherms for monolayer and multilayer adsorption,Kolloid Z.Z.Polym.235(1969)1203-1213.

[3]M.Jaroniec,Statistical interpretation of the Jovanović adsorption isotherms,Colloid Polym.Sci.254(1976)601-605.

[4]M.L.Huggins,Solutions of long chain compounds,J.Chem.Phys.9(1941)440.

[5]M.L.Huggins,Some properties of long-chain chain compounds,J.Phys.Chem.46(1)(1942)151-158.

[6]P.J.Flory,Thermodynamics of high polymer solutions,J.Chem.Phys.9(1941)660-661.

[7]P.J.Flory,Thermodynamics of high polymer solutions,J.Chem.Phys.10(1942)51-61.

[8]S.Brunauer,P.H.Emmet,E.Teller,Adsorption of gases in multimolecular layers,J.Am.Chem.Soc.60(2)(1938)309-319.

[9]R.B.Anderson,Modification of the Brunauer,Emmett and Teller equations,J.Am.Chem.Soc.68(1946)686-691.

[10]J.M.De Boer,The Dynamic Character of Adsorption,Clarendon Press,Oxford,1953.

[11]E.A.Guggenheim,Application of Statistical Mechanics,Clarendon Press,Oxford,1966.

[12]W.S.Loh,K.A.Rahman,A.Chakraborty,B.B.Saha,Y.S.Choo,B.C.Khoo,K.C.Ng,Improved isotherm data for adsorption of methane on activated carbons,J.Chem.Eng.Data 55(2010)2840-2847.

[13]Q.Wu,L.Zhou,J.Wu,Y.Zhou,Adsorption equilibrium of the mixture CH4+N2+H2on activated carbon,J.Chem.Eng.Data 50(2005)635-642.

[14]G.-M.Nam,B.-M.Jeong,S.-H.Kang,B.-K.Lee,D.-K.Choi,Equilibrium isotherms of CH4,C2H6,C2H4,N2,and H2on zeolite 5A using a static volumetric method,J.Chem.Eng.Data 50(2005)72-76.

[15]A.Vetere,A simple modification of the Flory-Huggins theory in non-polar or slightly polar solvents,Fluid Phase Equilib.34(1987)21-35.

[16]I.Mamaliga,W.Schabel,M.Kind,Measurements of sorption isotherms and diffusion coefficients by means of a magnetic suspension balance,Chem.Eng.Process.43(2004)753-763.

[17]Sibylle Kachel,Philip Scharfer,Wilhelm Schabel,Sorption isotherms of mixtures of polymers,proteins and electrolytes—measurement data and model predictions,Chem.Eng.Process.68(2013)45-54.

[18]H.C.Wong,S.W.Campbell,V.R.Bhethanabotla,Sorption of benzene,toluene and chloroform by poly(styrene)at 298.15 K and 323.15 K using a quartz crystal balance,Fluid Phase Equilib.139(1997)371-389.