高精度调频连续波雷达测距算法的研究

邱 菁，黄继伟，陈阿辉，柯玉山

(福州大学 物理与信息工程学院，福建 福州350002)

高精度调频连续波雷达测距算法的研究

邱 菁，黄继伟，陈阿辉，柯玉山

(福州大学 物理与信息工程学院，福建 福州350002)

在调频连续波(FMCW)雷达测距算法中，快速傅里叶(FFT)算法频谱分析的误差是由FFT频谱线之间间隔造成的。因此，为了提高FFT算法的测距精度，减少频谱分析的误差，提出了频移补偿的改进措施。频移补偿的频谱搬移因子的获取是利用频谱图对称性与最值和邻近两个谱线点坐标之间的距离差得到的。仿真实验的结果说明，该措施在不大幅提高测距时间的情况下得到的最值更接近实际峰值，可以较好地改进雷达的测距精度。

傅里叶变换；雷达；谱最大值估计算法；测距精度；频谱偏移

0 引言

常用的雷达测距有调频连续波和单脉冲雷达，其中调频连续波雷达具有较高的距离分辨率、低功率以及无测量盲区等特点[1-4]。调频连续波雷达广泛应用于雷达测距系统中，通过对信号进行采样和FFT算法分析进而提取测量距离的信息。由于FFT本身的“栅栏效应”，存在着较大的误差。而工业上如油罐的液位测量等应用中[5-6]，对测量的精度有很高的要求。人们常用提高频率细化率来提高精度，却增加了计算时间。因而产生了拟合法[7]、Rife算法[8]、谱最大值估计算法[8-11]、CZT[10-15]等方法来提高测距精度。其中CZT算法精度最高。本文对这些方法进行改进，设计了一个利用坐标中最值和邻近两个谱线点坐标之间距离差的方法与CZT相结合来改进测距精度，并对此进行了仿真和验证。

1 FMCW雷达测距原理分析和误差分析

文献[10-18]对雷达测量原理进行了分析。雷达测距原理是混频器通过雷达测距系统的天线获得发射和接收信号，从而得到差频信号[16-18]，通过差频信号的主频来提取距离信息，然后对距离信息进行数字信号处理获得目标距离。图1是发射信号与回波信号的时域关系。

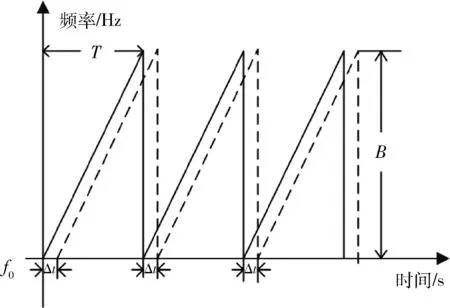
图1 发射信号与回波信号时域关系

图1中实线为雷达信号发射器发出的发射信号频率与时间的关系，虚线则为接收到的回波信号。雷达发射信号的本振信号与接收信号经过混频器混频之后可以得到差频信号。要获得所测量的距离就需要利用差频信号进行傅里叶变换，获取频谱图的最大采样值。

傅里叶变换就是把连续的时间利用加窗函数进行截断，截断成N点满足DFT在时域和频域上的离散信号的要求。而这些离散点之间存在着间隔，会受到栅栏效应的影响，所以FFT处理后采样点之间的间隔△R使得信号处理后的峰值会相对理论峰值偏左或者偏右。所以通过最大采样点的频率值计算出来的距离会产生△R/2的测距误差。其中这N个离散的谱线包络可以近似为一条曲线，但与理论的曲线相比，并不是对称的。为了减少误差，可以通过增加N点的大小，当大量增加N点的值时，采样点间隔会越来越密，包络的峰值也会不断增大，两侧的值也就越来越接近，逐步形成一个类似抛物线的对称曲线，而测得的距离误差也随之降低。但是运算量会大大增加，处理的速度也会变慢，对雷达系统的实时性造成不少影响[8-12]。

2 利用频谱图坐标估计最大采样点

对于谱最大值估计算法，文献[9-10]提到当理论的采样点与实际的采样点一致时，次大值就为0。但该方法也无法保证理论与实际的采样点的最大值是一样的，所以次大值不为零。由于FFT频谱图是对称的，也就可以近似认为频谱图中最大采样值点到相邻的两点的距离是相等的。由于FFT存在的栅栏效应两边的距离不一致，即存在最大值两边的次大值不一样。根据排序分为3个大小不一样的幅度值，以最大值为圆心，最大值与次大值的距离为半径画圆可以交于最大值与第三大值两点所在的直线上，两者之间会有距离差，而当两者之间的距离差小于某个值时，可以认为此时最大值点就是所要找的最大采样点，如图2所示。

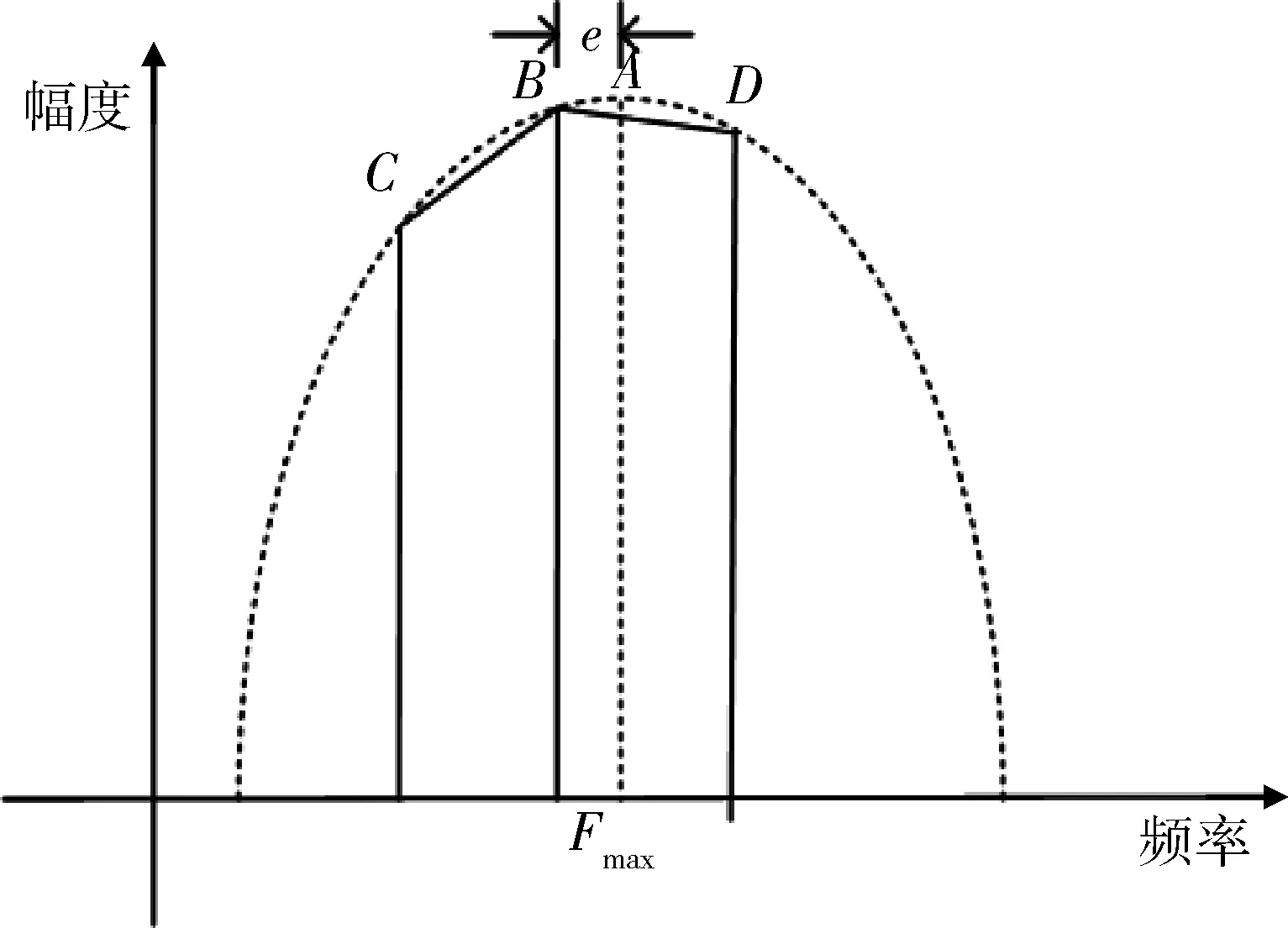
图2 频谱图

取频谱图上最大值及相邻两边的值B(f1,k1)、C(f3,k3)、D(f2,k2)，其中B对应的谱线是频谱线上的最大值,D是谱线的次大值，C是第三大值。则频谱的最大值A在B～D之间，由于距离谱是关于最大值对称的,因此可以认为当B与A重合时，D的对称点为C。

首先设定误差为Δf1，然后通过对最大值点到两个相邻序列的距离差Δk的分析，取BC、BD在坐标轴上线段距离的差值即距离差的一半作为估值点带入距离公式获得相应的值Δf，再通过比较BD、BC距离的大小来判断B点相对于最大值偏左还是偏右，把频谱左右移动Δf就可以获得B的新坐标值，可以得到新的距离差Δk以及Δf，对比Δf，若Δf1<Δf，需要重新对频谱进行移动，重复上面的方法，直到细分的Δf小于误差为止。该方法就是通过缩小距离差来获得最大值点。设D、B、C分别是频谱的次大值、峰值和第三大值，A为实际的频谱峰值，则线段BC与线段BD相等，B在D的左侧。若B与主瓣实际的峰值一样，根据距离相等可得：

(1)

若B与主瓣的实际峰值不一样，可以设两者的距离差为Δk，有：

(2)

设B点与主瓣峰值中心点的差值为Δf。设主瓣的中心点坐标为(f1+Δf,k1+Δk1)，由式(1)可得：

(3)

化简可得：

(f1+Δf-f3)2+(k1+Δk1-k3)2=(f2+Δf-f3)2+(k2+Δk1-k3)2

(4)

(5)

其中对于频谱上最大的3个点是序列号相邻的3个值，则可得f1、f2相差2个序列且f1+f2=2×f3。当整个频谱左右移动时，B、C、D所在的点的幅值也会相应增加或减少，设Δk1、Δk/2近似相等，则把式(2)结果带入到式(5)即可解出Δf。

(6)

然后整个频谱平移Δf，至于平移的方向需要依靠最大值和次大值的序列号的大小来决定。若次大值f2f3,则整个频谱右移。

再次获得此时的B、C、D3个点的新坐标，设误差为Δf1，当BC、BD的距离误差大于这个值则重复上面的步骤；当BC、BD的距离误差小于这个值，结束运行。所得到的B点就是峰值点。图3为改进后的算法流程图。

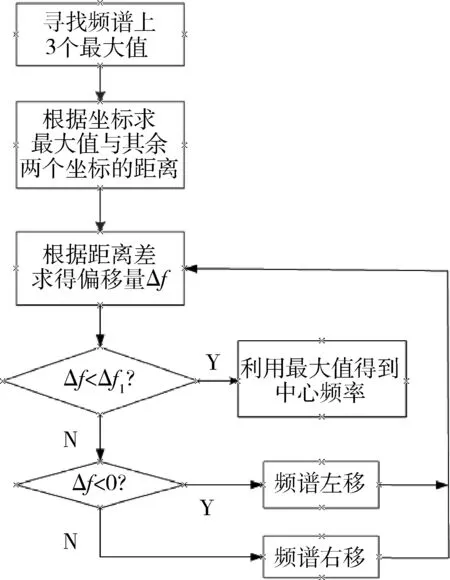
图3 改进算法流程图

3 仿真与验证

对上述所述的方法进行仿真和验证，并对比不同距离下不同方法的仿真程序运行的精度。雷达发射波的仿真条件为：调频信号的带宽B为109Hz；锯齿波调制信号的周期T为0.2 s；中心频率为24×109Hz。

对雷达的发射信号、回波信号、差频信号进行仿真，如图4、图5所示。

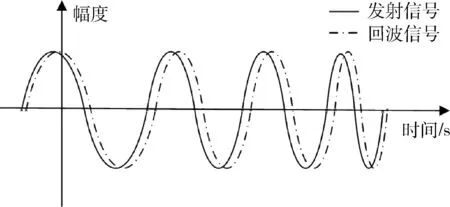
图4 发射信号与回波信号

图5 差频信号仿真

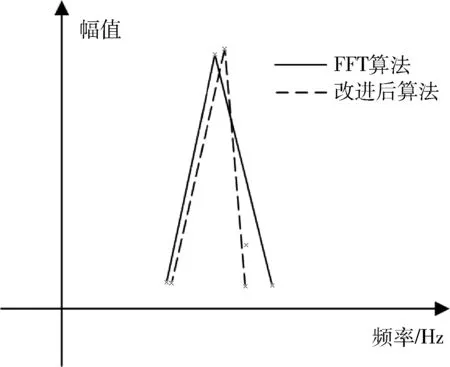
图6 仿真结果

设定目标的位置为100 m，得到如图6所示的频谱。根据FFT法，取N=1 024，目标所在的位置为99.61 m，误差为0.39%，然而经过最大值法得到目标所在的位置为99.98 m，误差为0.02%。

设定距离范围为10～100 m，目标为单目标时的计算机仿真结果见表1。

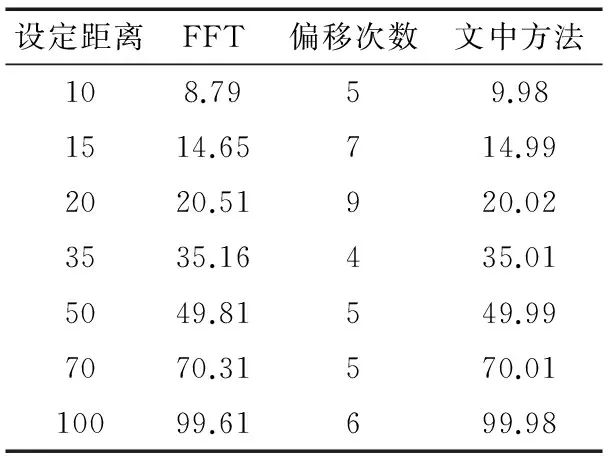
表1 单目标时的仿真结果

4 结束语

本文对雷达系统测距过程和原理进行分析，对测距算法进行一定改进，利用坐标的距离差提出了一种简单估计目标真实位置的方法，并将该方法与传统的快速傅里叶变换进行了对比。仿真实验结果说明该方法可以较好地改进雷达的测距精度。经过对时间的测量，FFT算法用时0.02 s，改进后用时0.034 s，频谱平移的次数在10次以内，对时间的影响不大。

[1] 包敏.线性调频连续波雷达信号处理技术研究与硬件实现[D]. 西安：西安电子科技大学，2009.

[2] 郭云，余奎，陈坚.几种连续波雷达系统参数设计和信号处理方法[J].电子科技,2015，28(2):158-163.

[3] 孙艳敏，周长林，常青美,等.减少防撞雷达虚假目标的信号处理研究[J]. 微型机与应用，2011，30(18):46-51.

[4] 胡玉兰，赵子铭，片兆宇.高分辨雷达一维距离像的融合特征识别[J]. 微型机与应用，2015，34(4):52-57.

[5] ZHU L, DONG L, LIU S D, et al. Self-adaptive frequency estimation algorithm of improving liquid level measurement precision of LFMCW radar[C]. 2010 International Conference on Microwave and Millimeter Wave Technology(ICMMT), IEEE, 2010:1626-1628.

[6] 王保华．近程LFMCW 雷达测距系统的研究与实现[D]. 重庆：重庆大学，2012．

[7] 周清晨，徐海洲，常城，等.基于抛物线拟合方法的提高雷达测距精度研究[J].信息通信，2016(6):8-9.

[8] 于卫东，涂亚庆，詹启东，等，基于改进Rife算法的LFMCW雷达测距方法及实现[J].电子测量与仪器学报，2015，29(4)：550-557.

[9] 徐军荣，于盛林.提高FMCW雷达测距精度的谱最大值估值算法[J].计算机技术与发展，2009，19(4):73-79.

[10] 王琨.调频连续波雷达在雷达测距中的算法研究[D]. 天津：河北工业大学，2013.

[11] 韩辉，冷建伟，安飞.FMCW雷达物位系统的算法设计[J]. 天津理工大学学报，2011，27(4)：27-31.

[12] 朱恺，秦轶炜，许建中，等．四种提高FMCW测距精度的方案及性能分析[J]．无线电工程，2015，45(1):20-25.

[13] 谭晓衡，周帅，黄振林．基于小波包的24 GHz LFMCW雷达测距方法[J]．系统工程与电子技术，2013，35(3):522-526.

[14] 陈璟.数字信号处理中加窗插值FFT算法的研究[J].黑龙江科学，2013，4(4):40-42.

[15] 侯盼卫,杨录,岳文豹.应用FFT的高精度FMCW雷达频率测量算法[J].自动化仪表,2014,35(3):17-19.

[16] 陈伟民，李存龙，基于微波雷达的位移/距离测量技术[J].电子测量与仪器学报， 2015,29(9):1251-1265.

[17] 肖玮，涂亚庆，刘良兵，等．多段同频正弦信号频谱融合的LFMCW雷达测距算法[J]．仪器仪表学报，2013,34(1):94-103.

[18] 郑大青，陈伟民，章鹏，等.非调制连续微波雷达发射机泄漏影响研究[J].仪器仪表学报，2014,35(4):775-780.

Research on high precision FMCW radar ranging algorithm

Qiu Jing, Huang Jiwei, Chen Ahui, Ke Yushan

(College of Physics and Information Engineering, Fuzhou University, Fuzhou 350002, China)

In FMCW radar ranging algorithm,the error of spectrum analysis of FFT algorithm is caused by the interval between FFT spectrum lines. Therefore, in order to improve the ranging precision of FFT algorithm, reduce the error of the frequency spectrum analysis, the messures about the improvement of frequency shift compensation are proposed. Using spectrum symmetry and the distance between the adjacent two spectral lines point coordinates to get the spectrum shift of frequency shift compensation factor. The results of simulation experiments show that the measures can get the most value which is closer to the actual peak by wasting a little time. And it can improve the ranging precision of radar better.

FFT; radar; spectral maximum estimation algorithm; range precision; frequency offset

福建省科技计划项目(2014H0026)

TN953+.2

A

10.19358/j.issn.1674- 7720.2017.09.007

邱菁，黄继伟，陈阿辉，等.高精度调频连续波雷达测距算法的研究[J].微型机与应用，2017,36(9)：22-24，27.

2017-01-14)

邱菁(1992-)，通信作者，女，硕士研究生，主要研究方向：数字信号处理。E-mail:397279938@qq.com。

黄继伟(1976-)，男，博士，副教授，主要研究方向：射频电路与系统。

陈阿辉(1991-)，男，硕士研究生，主要研究方向：嵌入式系统。