时间模上一类二阶非线性动态方程振荡性的新结果
杨甲山,张晓建
(1.梧州学院信息与电子工程学院,广西梧州543002; 2.梧州学院复杂系统仿真与智能计算实验室,广西梧州543002; 3.邵阳学院理学与信息科学系,湖南邵阳422004)
时间模上一类二阶非线性动态方程振荡性的新结果
杨甲山1,2,张晓建3
(1.梧州学院信息与电子工程学院,广西梧州543002; 2.梧州学院复杂系统仿真与智能计算实验室,广西梧州543002; 3.邵阳学院理学与信息科学系,湖南邵阳422004)

研究了如下一类时间模T上的二阶非线性的中立型变时滞泛函动态方程的振荡性,其中φ(u)=|u|λ-1u(λ>0为任意常数).通过引入一对黎卡提变换,并结合时间模上的理论及不等式技巧,得到了该方程振荡的2个新准则,推广并改进了现有文献中的一些结果.最后,举了2个例子说明了本文定理的重要性.
振荡性;时间模;泛函动态方程;变时滞
0 引言
振荡(亦称振动)作为一种物理现象,广泛存在于自然科学和工程技术中,如控制系统中的自激振荡,同步加速器中波束的振动,化学反应过程中的复杂振荡等等.这些现象可以统一为方程的振荡理论,因此,振荡理论作为微分方程的定性理论之一受到了学者们的广泛关注.近来,德国学者Stefan Hilger在其导师Bernd Aulbach指导下于1988年首次提出了时间模(time scales,也称时间测度链,时间尺度,时标,时间轴等)的概念,并由此创立了时间模上动态方程(dynamic equations on time scales)的理论.之后,这一新领域内有关问题(特别是时间模上动态方程的振动性等定性理论问题)的研究引起了国内外学术界和科研工作者的极大兴趣,并发表了许多这方面的专著及研究论文,见文献[1-19]及其参考文献.笔者研究时间模上如下一类二阶非线性中立型变时滞泛函动态方程

的振荡性,式中φ(u)=|u|λ-1u(其中λ>0为实常数);T为任意时间模,且supT=∞.设t0∈T且t0>0,则定义时间模区间为[t0,∞)T=[t0,∞)TT.方程(1)的解及其振荡性的定义,可参见文献[1-2].本文只讨论方程(1)的最终不恒为零的解.我们考虑如下条件.
(H1)τ,δ∶T→T,满足τ(t)≤t,且并且τ◦δ=δ◦τ.
(H2)τ是严格递增的,˜T=τ(T)⊆T是一时间模,τ◦σ=σ◦τ,且τΔ(t)=τ0>0,δ(t)≥τ(t).
(H3)A(t)∈Crd(T,(0,∞));B(t)∈Crd(T,R),且0≤B(t)≤b0<∞(这里b0是非负实常数).
(H4)g∈C(R,R),且ug(u)>0(u/=0),并且有g(u)/u≤η(u/=0),这里常数0<η≤1.
(H5)f∈C(T×R,R),uf(t,u)>0(u/=0),且∃P(t)∈Crd(T,(0,∞))使得|f(t,u)|≥P(t)|u|(u/=0).
关于时间模上中立型动态方程的振荡性,近年来,虽然出现了很多研究成果[8,11-19],但是在这些研究成果中,对中立项的系数函数B(t)都有限制条件0≤B(t)<1,而当B(t)≥1或者B(t)≤0时方程的振荡准则却几乎没有.本文是文[1]和[2]的继续,文[1]在

且0≤B(t)≤b0<∞的条件下得到了关于方程(1)的3个新振荡准则,改进了现有文献中对中立项系数函数B(t)的限制条件∶0≤B(t)<1.但我们注意到,其结果是在0<λ≤1时得到的,而当λ>1时其振荡准则显然不成立;文献[2]同样在(C1)成立且0≤B(t)≤b0<∞的条件下得到了方程(1)当λ≥1时的振荡的3个充分条件,拓广了文献[1]的结果,推广、改进了现有文献中的结论.但另一方面,对于著名的Euler方程

来说,显然不满足条件(C).此外,由于
本文将在条件

且0≤B(t)≤b0<∞下建立方程(1)的振荡准则,推广并改进现有文献中的结果,统一了相应的微分方程和差分方程的振荡性结论.
1 在条件(C2)下方程(1)的振荡准则
引理1[3]设x(t)是Δ可微的且最终为正或最终为负,则有

引理2[4]设A>0,B>0和λ>0均为常数,则当x>0时,
引理3[11]若τ(t)是严格递增的,˜T=τ(T)⊆T是一时间模,τ◦σ=σ◦τ.设x∶˜T→R,如果τΔ(t)和xΔ(τ(t))存在(t∈Tk),则(x(τ(t)))Δ存在,且

定理1设条件(H1)—(H5)及(C2)成立,若存在函数φ∈使得当0<λ≤1时

其中ki>0(i=1,2,3,4)是常数,函数

则方程(1)在[t0,∞)T上是振荡的.
证明反证法.设方程(1)在[t0,∞)T上有一个非振荡解x(t),不妨设x(t)是最终正解(当x(t)是最终负解时类似地可证),即存在t1∈[t0,∞)T,使得当t∈[t1,∞)T时,有x(t)>0,x(τ(t))>0,x(δ(t))>0.记y(t)=x(t)+B(t)g(x(τ(t))),则当t∈[t1,∞)T时y(t)>0.由方程(1),得

因此A(t)φ(yΔ(t))在[t1,∞)T上严格递减且最终定号,进而yΔ(t)或者最终为正或者最终为负.所以,我们只需考虑如下两种情形.

情形(a)yΔ(t)>0(t∈[t1,∞)T).当0<λ≤1时,由文[1]中定理1的证明,可得到一个与(3)式矛盾的结果;当λ>1时,由文[2]中定理1的证明,可得到一个与(5)式矛盾的结果,故这种情形方程(1)是振荡的.
情形(b)yΔ(t)<0(t∈[t1,∞)T).此时,由文献[1]中的定理1(也可由文献[2]中的定理1)的证明过程知,下式仍然成立.

当0<λ≤1时,根据引理1,可得

定义函数v(t)如下∶

显然有v(t)≤0(t∈[t1,∞)T).
由(7)式不难看出,A(t)φ(yΔ(t))=A(t)(-yΔ(t))λ-1yΔ(t)是单调减少的,因此,当s∈[t,∞)T时,

由(11)式可得

上式对s两边从t到u(u≥t∈[t1,∞)T)积分,可得

在上式中,令u→∞,则有y(t)+A1/λ(τ(t))yΔ(τ(t))ζ(t)≥0,从而可得

于是,应用(10)式,不难得到

另一方面,对(10)式两边求Δ-导数,并注意到(9)、(11)式及yΔ(t)<0,得
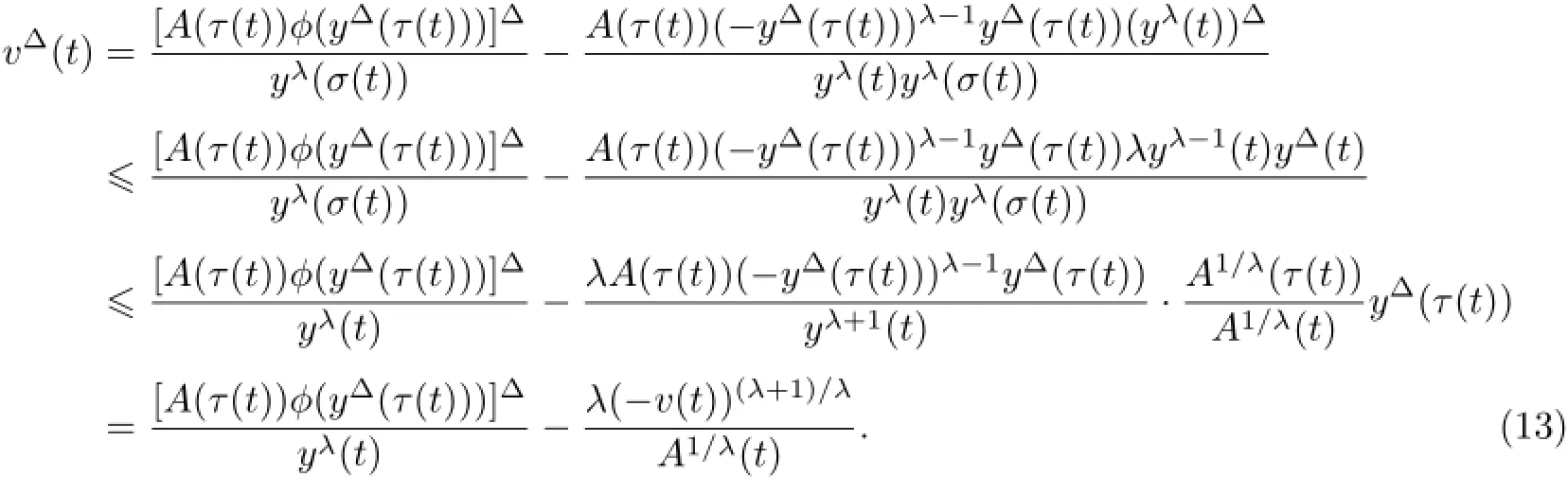
类似地,再定义函数w(t)如下

则同样有w(t)≤0,t∈[t1,∞)T,且

综合(13)和(15)两式,并注意到(8)式,得

再次利用A(t)(-yΔ(t))λ-1yΔ(t)的单调减少性,当s∈[t1,∞)T时,有

这里常数kλ=-A(t1)(-yΔ(t1))λ-1yΔ(t1)>0.因此A(s)(-yΔ(s))λ≥kλ,亦即yΔ(s)≤-kA-1/λ(s).两边积分,得

上式中,令u→∞,得y(t)≥k(s)Δs=kζ(t),亦即

代入(16)式,得
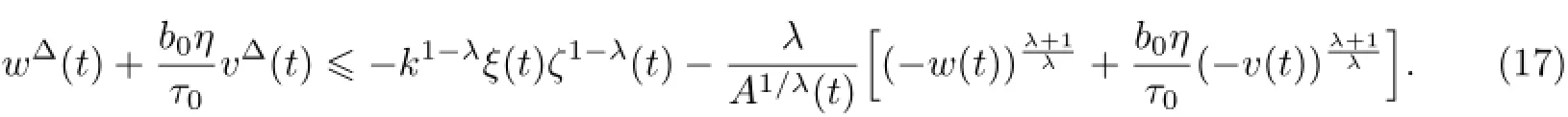
(17)式两边同时乘以ζλ(σ(t))后再积分,并利用时间模上的分部积分公式

及引理2,再注意到ζΔ(t)=-A-1/λ(t)<0且[ζλ(t)]Δ≥-λζλ-1(σ(t))A-1/λ(t),可得

于是由上式,并利用(12)和(14)两式,可得

这与(4)式矛盾.
当λ>1时,讨论完全类似于0<λ≤1的情形.由引理1,此时(9)式为

就可得到相同的(16)式.
因为y(t)>0,yΔ(t)<0(t∈[t1,∞)T),所以y(t)≤y(t1)=k,即y1-λ(t)≥k1-λ.将其代入(16)式,得
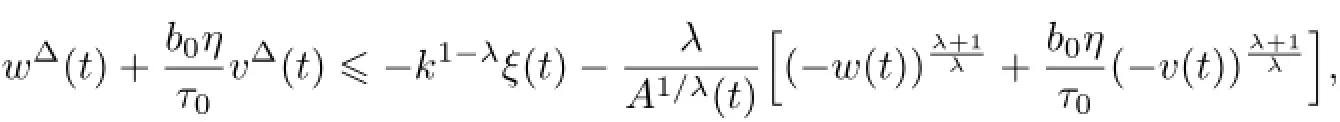
类似地(即上式两边同乘以ζλ(σ(t))后再积分,并采用与上面类似的处理方法),可得到一个与(6)式矛盾的结果.所以这种情形方程(1)也是振荡的.定理证毕.
定理2设条件(H1)—(H5)及(C2)成立,若存在函数φ∈C1rd([t0,∞)T,(0,∞))使得当0<λ≤1时(3)式成立,且
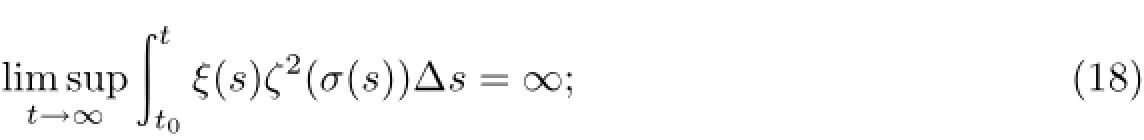
当λ>1时(5)式成立,且

其中函数ξ(t)和ζ(t)的定义如定理1.则方程(1)在[t0,∞)T上是振荡的.
证明同定理1的证明.当0<λ≤1时,可得(17)式,将(17)式的t改成s,两边同乘以ζλ+1(σ(s))后再积分,并利用时间模上的分部积分公式,且注意到ζΔ(t)=-A-1/λ(t)<0, [ζλ(t)]Δ≥-λζλ-1(σ(t))A-1/λ(t),可得


同理,根据(12)式,可得

于是由(20)式,得

这与(18)式矛盾.
当λ>1时,完全类似地,可得到一个与(19)式矛盾的结果.定理证毕.
注1结合文献[1-2]中的定理2和定理3,运用与定理1和定理2完全相同的方法,可得方程(1)在条件(C2)下的Philos型和Kamenev型振动准则.为节省篇幅,在此就不赘述了.
注2本文在积分R∞t0A-1/λ(s)Δs收敛的情况下给出了方程(1)的振荡准则,去掉了现有文献中对中立项系数函数的限制条件0≤B(t)<1.从下面例子看出,本文定理改进了现有文献中已有的一些结果.此外,从定理的证明过程可以看出,条件(H2)中的τΔ(t)=τ0还可修改为更一般的形式∶τΔ(t)≥τ0>0,且这样修改后,文献[1-2]及本文的所有定理均成立.
2 例子
例1考虑二阶微分方程

其中常数γ>0.显然,这是著名的欧拉(Euler)微分方程.令A(t)=t2,B(t)=0,P(t)=γ,τ(t)=δ(t)=t,λ=1,则τ0=1,b0=0.不难验证条件(H1)—(H5)及(C2)都是满足的.注意到此时T=R,ξ(t)=min{P(t),P(τ(t))}=γ,取φ(t)=t,则当γ>1/4时,有

因此条件(3)和(4)都满足,于是由定理1知,当γ>1/4时方程(E1)是振荡的.显然,这与已知的结果完全一致.
注3值得注意的是,因此文献[10]中定理4.3和定理4.4的条件(4.15)、文献[16]的条件(C3)以及文献[18]的条件(4.14)均不满足,所以这些文献中的有关定理都不能用于方程(E1).此外,若将文献[6]中的定理3.5,或者文献[9]中的定理4.3,或者文献[17]中的定理4.3用于方程(E1),只能得到“方程(E1)的每一个解或者振荡或者收敛于零”,这是一个不确定的结果,即不能判定方程的振荡性.其他文献如[1-2,8,11-14,19]中的定理也不能用于方程(E1).
例2考虑时间模T=2Z上的二阶动态方程

这里λ=3,A(t)=t4,B(t)=2+sint,显然,这是一个二阶2-差分方程且具有非线性中立项.由于0<B(t)=2+sint≤3=b,0

因此条件(H1)—(H5)及(C2)都满足.为了简单,在定理1中取φ(t)=1,则由于ξ(t)=
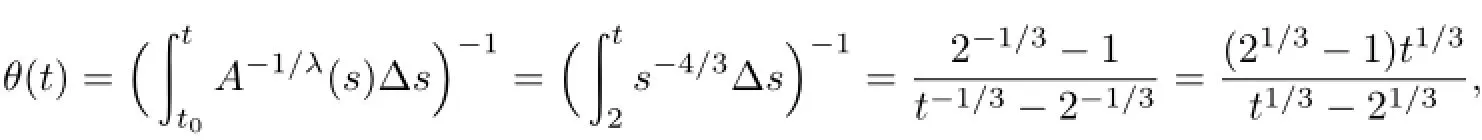
从而θ(τ(t))

因此,定理1的条件全部满足,于是由定理1知,方程(E2)是振荡的.
注4由于例2中方程的中立项的系数函数不满足条件0≤B(t)<1,且中立项是非线A-1/λ(s)Δs又是收敛的,所以文献[1-19]中的定理都不能用于方程(E2).
[1]张晓建,杨甲山.时间模上二阶非线性动态方程振荡性的新结果[J].浙江大学学报(理学版),2014,41(5):499-505.
[2]杨甲山,黄劲.时间模上一类二阶非线性动态方程振荡性的新准则[J].华东师范大学学报(自然科学版),2015(3):9-15.
[3]BOHNER M,PETERSON A.Dynamic Equations on Time Scales,an Introduction with Applications[M]. Boston:Birkhauser,2001.
[4]SAKER S H.Oscillation of second-order nonlinear neutral delay dynamic equations on time scales[J].J Comput Appl Math,2006,187:123-141.
[5]杨甲山,谭伟明,覃学文,等.时间模上二阶非线性阻尼动力方程的振动性分析[J].浙江大学学报(理学版),2016,43(1): 64-70.
[6]孙一冰,韩振来,孙书荣,等.时间尺度上一类二阶具阻尼项的半线性中立型时滞动力方程的振动性[J].应用数学学报,2013, 36(3):480-494.
[7]杨甲山.时间测度链上具非线性中立项的二阶阻尼动力方程的振动性[J].浙江大学学报(理学版),2012,39(3):261-265.
[8]杨甲山.时间测度链上二阶动力方程的振动准则[J].华东师范大学学报(自然科学版),2012(3):17-23.
[9]张全信,高丽.时间尺度上具阻尼项的二阶半线性时滞动力方程的振动准则[J].中国科学:数学,2010,40(7):673-682.
[10]张全信,高丽,刘守华.时间尺度上具阻尼项的二阶半线性时滞动力方程的振动准则(II)[J].中国科学:数学,2011,41(10): 885-896.
[11]HAN Z L,LI T X,SUN S R,et al.Oscillation for second-order nonlinear delay dynamic equations on time scales [J].Advances in Dif f erence Equations,2009,2009:1-13.
[12]杨甲山,方彬.时间模上一类二阶非线性中立型泛函动态方程的振荡性[J].内蒙古师范大学学报(自然科学汉文版),2016, 45(5):603-609.
[13]杨甲山,方彬.时间测度链上一类二阶非线性时滞阻尼动力方程的振动性分析[J].应用数学,2017,30(1):16-26.
[14]杨甲山,谭伟明,苏芳,等.时间模上二阶非线性中立型时滞泛函动态方程的振荡性[J].南开大学学报(自然科学版),2015, 48(3):24-31.
[15]张晓建,杨甲山.时标上三阶时滞动力方程的振动性和渐近性[J].华东师范大学学报(自然科学版),2014(3):51-59.
[16]ERBE L,HASSAN T S,PETERSON A.Oscillation criteria for nonlinear damped dynamie equations on time scales[J].Apple Math Comput,2008,203:343-357.
[17]张全信,高丽,刘守华.时间尺度上具阻尼项的二阶半线性时滞动力方程振动性的新结果[J].中国科学:数学,2013,43(8): 793-806.
[18]ZHANG Q X.Oscillation of second-order half-linear delay dynamic equations with damping on time scales[J]. Journal of Computational and Applied Mathematics,2011,235:1180-1188.
[19]杨甲山.时间测度链上一类二阶Emden-Fowler型动态方程的振荡性[J].应用数学学报,2016,39(3):334-350.
(责任编辑:林磊)
New results of oscillation for certain second-order nonlinear dynamic equations on time scales
YANG Jia-shan1,2,ZHANG Xiao-jian3
(1.School of Information and Electronic Engineering,Wuzhou University, Wuzhou Guangxi543002,China; 2.Laboratory of Complex System Simulation and Intelligent Computing,Wuzhou University,Wuzhou Guangxi543002,China; 3.Department of Science and Information,Shaoyang University, Shaoyang Hunan422004,China)

oscillation;time scales;functional dynamic equations;variable delay
O175.7
A
10.3969/j.issn.1000-5641.2017.03.006
1000-5641(2017)03-0054-10
2016-08-28
广西教育厅科研基金(2013YB223);硕士学位授予单位立项建设项目(桂学位[2013]4号);梧州学院2014年校级科研重大项目(2014A003);湖南省教育厅科研项目(10C1189)
杨甲山,男,教授,研究方向为微分方程的理论及应用.E-mail:syxyyjs@163.com.
张晓建,女,讲师,研究方向为微分方程的理论及应用.E-mail:zxj2006a@163.com.

