Emathema:在线的方程自动求解平台

杨乐,柳银萍,李志斌

(华东师范大学计算机科学技术系,上海200062)

Emathema:在线的方程自动求解平台

杨乐,柳银萍,李志斌

(华东师范大学计算机科学技术系,上海200062)

微分方程在现代科技、工程领域中的作用日益显著,本课题组多年来在微分方程可积性和解析求解方面做了很多机械化工作,研发出了一系列Maple应用软件.基于这些应用软件、计算机代数系统Maple及一些开源技术,课题组研发了一个在线的开放的方程自动求解平台Emathema,为用户提供便捷的代数计算和绘图服务.在此平台上,用户不仅可调用已嵌入的Maple外部应用软件求解非线性代数和微分方程(组),而且在交互方式下可进行几乎所有和方程相关的简单符号计算,所有的计算结果均以可视化的方式输出.

符号计算;在线计算平台;Maple应用软件;微分方程

0 引言

众所周知,在科学研究和工程技术领域,比如∶数学、物理、生物学、生态学、金融学、气象学、航空航天、社会学以及其他领域,不少研究人员与工程技术人员在工作中需要去求解特定类型的方程,尤其是数学物理方程.随着计算机技术及计算机代数系统的不断发展,人们的计算能力大大提升了,微分方程的应用领域也因此得到了极大的拓展.目前,微分方程已成为现代数学中应用领域最广,研究最为活跃的数学分支之一.很多学者借助计算机代数系统(CASs)作为代数推导和证明的重要工具,新的研究成果不断涌现.特别地,一些构造非线性微分方程解析解的直接代数方法相继诞生,如∶混合指数法、双曲正切法及其变形和推广、椭圆函数法及其变形和推广等等.我们团队基于Maple几乎实现了上述所有的方法,其中的应用软件可自动推导出非线性微分方程特定类型的解析解.虽然有部分同行索要并使用这些应用软件,但相对于对这些软件有需求的用户群体而言,这些软件的的利用率很低.

互联网的高速发展使得在线数学计算和在线教育越来越流行.近年来,开发在线的计算软件已经成为了公认的研究热点.不少科研机构或公司已研发出他们的在线计算软件或教育软件,其中,在线科学计算软件包括以IAMC[1],WebMathematica[2],IPython[3], Distributed Mathematica[4]为代表的分布式符号计算系统,以Grid-Elimino[5]为代表的网格计算软件,以AsirPad[6]为代表的面向移动设备的在线计算系统以及知识型计算引擎Wolfram Alpha[7],而在线的数学教育软件包括ActiveMath[8],Maple T.A.[9],DMAS[10]等等.本课题组成员曾基于Maxima研发了在线的可视化计算系统iMathema[11].目前,我们对该系统还在不断拓展和完善中.

随着人们科学计算能力的不断提升,微分方程的应用范围也越来越广泛,目前,从自然科学到社会科学几乎所有的学科领域都越来越热衷于采用微分方程方法求解问题.国际上已诞生了几个专门的微分方程网站[12-13],国际、国内的超算中心也建立了专门的微分方程研究中心[14-15].本文为了服务各行各业的科研和工程技术人员,在我们前期工作的基础上,基于Command-line Maple和一些Maple应用软件等研发了一个在线的方程自动求解平台Emathema.在该平台中,用户除了可使用已嵌入的Maple应用软件求解非线性微分系统,还可在交互方式下进行与方程有关的几乎所有的简单计算和绘图.另外,也可运行Maple中的基本命令.和国内外已有的在线计算软件相比,该计算平台更具专业性,是目前独具特色的方程自动求解平台.另外,该平台的使用界面友好,用户只需通过Web浏览器即可访问和使用该平台求解问题,不需要在客户端安装任何符号计算系统.除此之外,该平台还支持将在线的演算过程和程序运行结果导出到Maple的Worksheet文档中,供用户下载后续使用.我们的长远目标是研发一个在线的功能庞大的符号计算系统.

1 Emathema的原理与技术路线

1.1 Emathema的原理

Emathema是一个在线的B/S计算平台,其原理见图1所示.

如图1,Emathema进行科学计算的过程可概括如下∶Emathema计算平台的服务器端安装有Maple计算软件及处理底层符号计算软件的输入和输出的PHP[16]脚本,同时还配置有合适的网络环境.当用户通过浏览器向Emathema提交计算请求后,Emathema会自动地选择相应的PHP脚本,该脚本通过命令行接口将相应的命令传递给Command-line Maple,然后Emathema利用其转换模块将得到的Maple格式的字符串输出结果进行相应的转换,进而Emathema的可视化输出模块将转换后的结果进行在线的可视化输出.

图1 Emathema进行科学计算的原理Fig.1 How scientific computations are executed in Emathema

Emathema计算平台具有如下特色∶第一,扩展性较强,底层可嵌入主流的符号计算软件,如∶Maple、Mathematica、Maxima等;第二,具有优越的在线可视化特性,即所有计算结果均以可视化形式输出;第三,具有良好的跨操作系统平台、跨设备、跨浏览器特性.目前,用户可通过几乎所有的主流浏览器,如Chrome,Firefox,IE,Safari,Opera等来访问和使用该平台;第四,在线系统,可随时随地使用.

1.2 技术路线

研发一个交互式的在线计算软件,首先需考虑其输入命令和输出计算结果的方式.通过查阅大量文献我们得知∶在线的计算软件中普遍采用如下几种输入方式∶①以线性字符串的方式进行输入,输入快捷.大部分主流的符号计算软件,如∶Command-line Maple、Mathematica Kernal、Maxima等底层的输入采用了此方式;②以交互式方式进行WYSIWYG(所见即所得)方式的输入,一般采用XML和样式表进行公式外观的控制.工作表模式下的Maple Worksheet、Mathematica Notebook、WxMaxima(Maxima的图形化界面)均使用了各自的样式表进行公式外观的控制,且三者的样式表有很多细节上的差异,进行计算时会将该二维公式转换为字符串后再进行处理;③其他输入方式,包括语音输入与语音识别相结合的方式和手写输入与手写识别相结合的方式等.通过语音输入虽比较方便,但由于数学公式没有规范的读法,且方言很难避免,极易引起歧义,故相应的语音识别和后期处理难度很大;手写输入虽然便利,但当输入的二维数学表达式难辨识或结构较复杂时,手写识别的准确度明显下降.总体而言,方式①更接近底层符号计算软件的内核,也更方便于进行其他后期操作,故Emathema选取了方式①.

在线的计算软件中普遍采用如下几种输出方式∶①线性字符串的形式,传输速度快,但不直观.大部分符号计算软件,如∶Command-line Maple、Mathematica Kernal、Maxima等底层的输出采用了此方式;②图片的形式,直观,但耗费带宽,传输速度较慢.在MathML标准[17]被广泛接受之前,此方式占主导地位;③字符堆砌的形式,无法较美观地显示结果复杂的公式.流行的符号计算软件Command-line Maple、Mathematica Kernal、Maxima在命令行中的二维输出(2D ASCII)采用了此方式,该方式下上标、下标、幂次等还算美观,但积分符号、极限以及其他结构更复杂的公式并不美观;④传输字符串文本,显示二维公式.采用这种输出方式,既能快速传输,也能直观显示二维数学表达式.目前有ASCIIMathML[18]、MathJax[19]这两种流行技术采用了此方式,并兼容所有主流浏览器.因而,Emathema采用了方式④,同时应用了ASCIIMathML和MathJax,其中ASCIIMathML用于可视化显示中缀字符串,而MathJax用于可视化显示LaTeX格式的字符串.

除了对输入、输出方式进行选择以外,在已有符号计算软件的基础上研发一个交互式的在线符号计算软件还需对符号计算软件的接口进行研究.我们一开始就重视跨操作系统的接口技术.对Maple而言,基于Maple底层内核,主要有两种方式能与Command-line Maple进行交互∶①Java+OpenMaple接口Java版,此接口下会创建一个Maple session会话,然后Maple engine对象即可执行部分Maple的基本命令;②PHP+Command-line Maple,此接口更接近于Maple底层,可以完成绝大部分Maple运算.我们对以上两种方式均进行了尝试,先使用OpenMaple接口Java版以及Struts 2框架搭建了一个通用的计算系统,此时发现对于绘图,OpenMaple接口的功能比较弱,这部分工作有待后续继续研究.接口②的可扩展性较强,该接口下Maple外部应用软件的Web接口较易实现.此外,Emathema实现接口②的方法不仅支持Maple,同时也支持Mathematica、Maxima.综合考虑之后,Emathema选了接口②.

Emathema是一个即时响应的实时交互式计算平台,采用了AJAX[20]异步通信方式, AJAX允许页面“安静地”向服务器发送请求,并获得计算结果,在原网页中输出,克服了同步通信方式响应后返回全新页面、通信时间过长、不能局部提交数据等不足.但由于原生AJAX较复杂,我们为此引入了一个轻量级的JavaScript库jQuery[21].jQuery兼容多种主流浏览器,且可简化AJAX应用的开发过程.jQuery保障了Emathema在不同的浏览器中均能正常使用.

2 Emathema的图形用户界面及其功能

目前,Emathema的底层主要使用了Command-line Maple,基于Maple及Maple外部应用软件,Emathema除了能使用已嵌入的Maple应用软件[22-25]求解代数及微分方程组外,还能提供简单代数计算和绘图服务.对于每一个合法的输入,相应的计算结果均能在线地可视化输出.用户只需在连网的状态下借助浏览器,并且不限于设备和操作系统平台就能使用Emathema的所有功能.本着“简单、易用”的原则,Emathema不仅设置了一个集成界面(在线的命令行界面),还为其中的部分应用软件提供了独立的图形化用户界面(GUI).限于篇幅,本文以下部分只介绍集成界面(见图2).

图2 Emathema的集成界面Fig.2 The integrated user interface of Emathema

集成界面主要由①下拉菜单,②命令输入区域,③可视化结果输出区域以及多个按钮(Computing,Plotting,Error Checking,Clear,Export Input as Worksheet,Export Outputas Worksheet)等组成,这些按钮的功能见表1所述.

表1 各个按钮的功能Tab.1 Functions of each button

在集成界面下,Emathema的功能主要由下拉菜单来控制,该下拉菜单设置了any,none和一些已被嵌入的应用软件名称等多个选项.

•当用户在下拉菜单中选择“none”时,用户可以使用Maple内置的常见代数命令和绘图命令,比如expand、solve、pdsolve、integrate、gcd、plot、plot3d等命令,也可以使用Maple内置的软件包,如with(linalg).此方式下还支持批量计算,即在命令输入区域中,当用户的输入不含空行时,所输入的命令将被视为一个块语句来执行.用户也可批量地输入多个块语句(每个块语句由一个或多个单语句组成,块语句内是以分号或冒号作为分隔符,块内允许换行,但不允许出现空行),块语句之间以一个或多个空行作为分隔符.图3展示了一个批处理计算的例子.

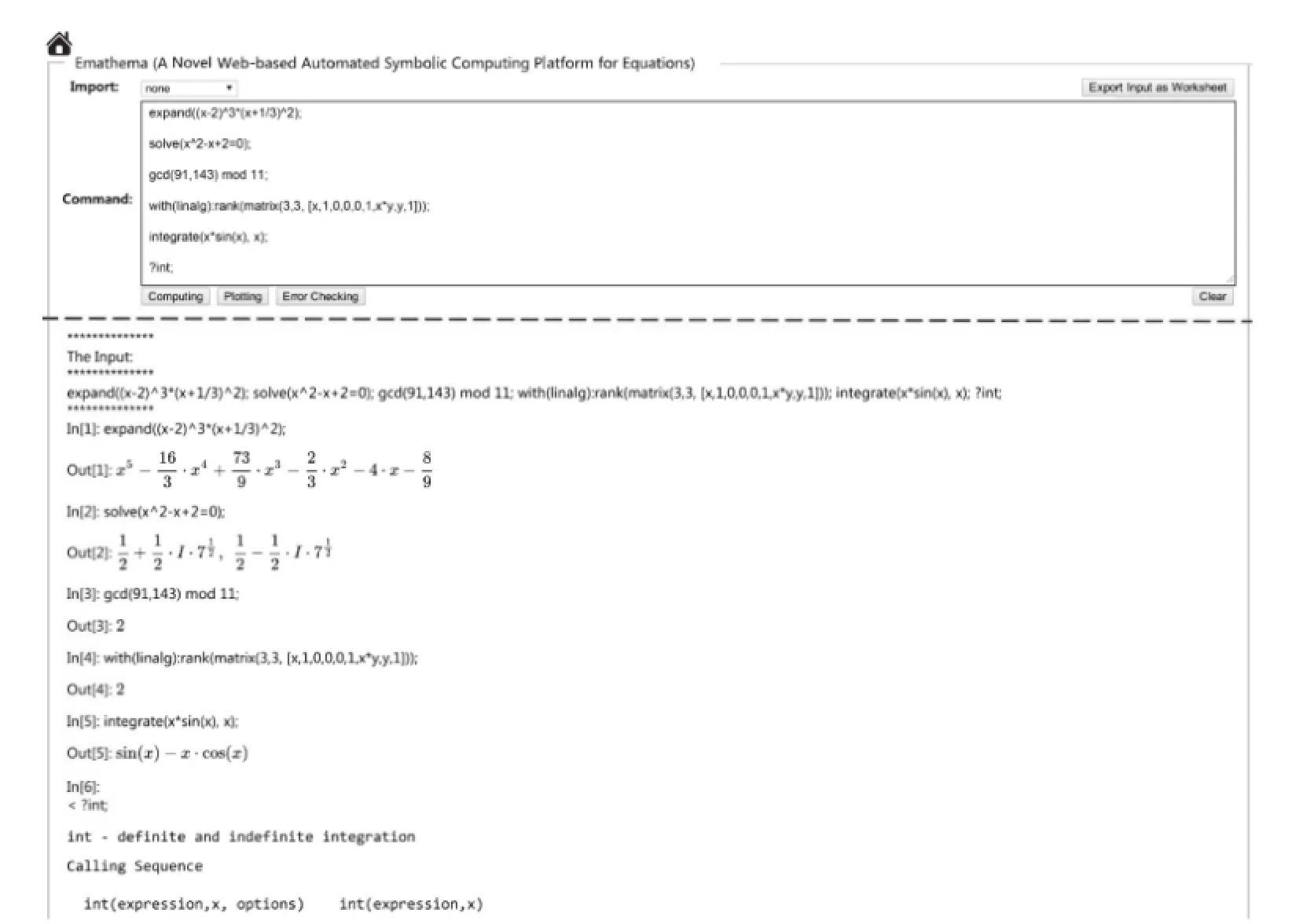
图3 批量计算的输入、输出Fig.3 The input and output of batch tasks

上述演算过程中输入的内容可通过“Export Input as Worksheet”按钮导出到一个Maple的Worksheet文档中,供用户后续下载使用.上述演算过程导出的Worksheet文档如图4所示.

图4 批量计算导出的Worksheet文档中的内容Fig.4 The content of Maple Worksheet file exported from the results

•当用户选择下拉菜单中的“any”时,系统会根据用户输入的with语句将相应的外部应用程序调入内存,此时,用户可调用已被读入内存的任何应用程序求解问题,如可使用我们研发的应用软件求解微分系统等.

下面以RATH软件[22]为例来说明此选项下外部应用软件的用法,如用RATH来求解如下的Ito’s 5th-mKdV方程∶

先用with命令导入RATH应用软件,然后调用RATH的主模块rath来求解该方程,其输入和输出结果见图5所示.

图5 集成界面中应用软件RATH的使用示例Fig.5 An example of using RATH under the integrated user interface

Emathema也可将程序的运行结果导出到Maple的Worksheet文档中,供用户下载和后续使用.图6是点击图5右下角的“Export Output as Worksheet”按钮导出的Worksheet文档.

图6 将RATH的计算结果导出到Worksheet文档示例Fig.6 A demo of Maple Worksheet file exported from results using RATH

•下拉菜单中的其他选项都是专门为已嵌入的外部应用程序设置的.在这些选项下,用户可调用相应的应用软件求解问题,如在RATH选项下,用户可调用软件RATH求解问题.也就是说,任何一个外部应用程序均可在两种选项下使用,即any选项和相应的应用程序选项.

另外,该平台是开放的,这样研发人员后续可不断地往系统中嵌入其他应用程序,如我们已将求解非线性代数方程组的一些经典软件,如Gr¨obner基方法程序包,王东明教授研发的Charsets包[26]及Epsilon程序库[27].王定康研究员研发的Wsolve包[28]等嵌入Emathema中,用户可选择下拉菜单中的“any”或“none”选项来使用它们.

如,下面调用Charsets包,使用其中的csolve命令来求解一个非线性代数方程(组).其输入和输出见图7所示.

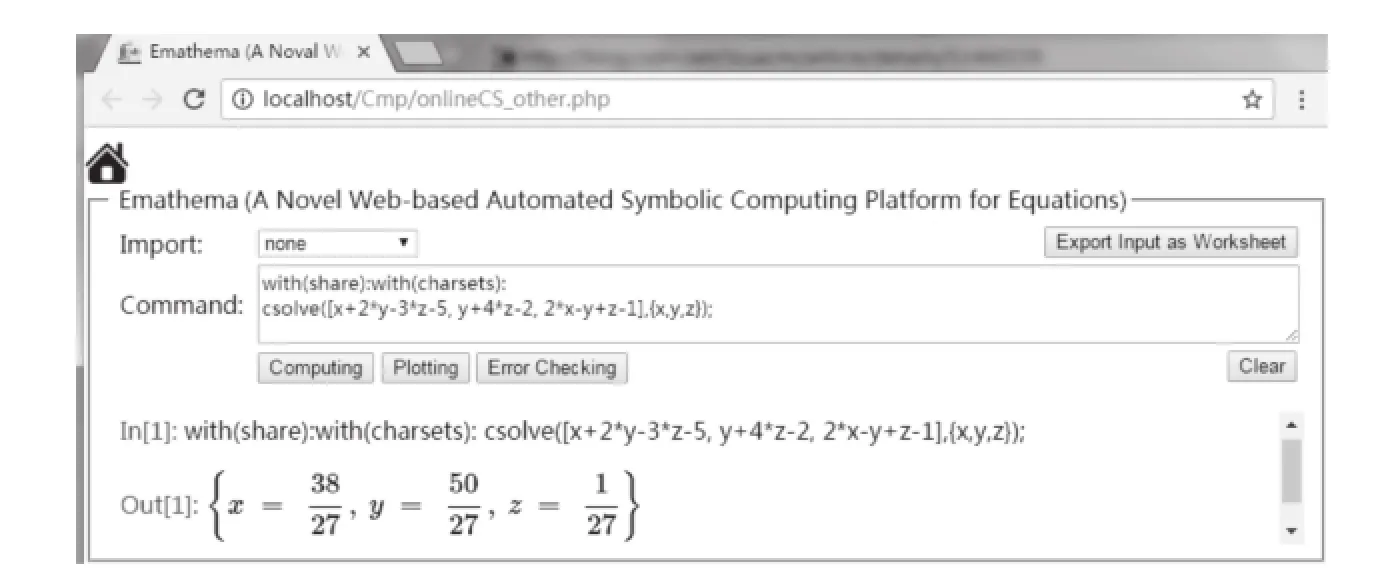
图7 Charsets包的使用示例Fig.7A demo of using Charsets package

此外,Emathema还为用户设计了详细的在线帮助手册.Emathema的所有功能在帮助手册中均有详细介绍.

3 结束语

该论文介绍了最新版的在线计算平台Emathema.在此平台上,用户不仅能调用已嵌入的Maple外部应用软件求解非线性微分系统和非线性代数方程(组),还能在交互方式下进行各种简单的符号计算,所有的计算结果均以可视化的方式输出.Emathema计算平台是我们课题组研发的“方程的在线计算和知识库平台”[29]的一部分,该在线平台还包括微分方程知识库、数学论坛和数学资源库等,该在线平台已在实验室内网服务器中使用,不久将会发布在公网中供广大用户使用.该在线平台是开放的,我们后续将继续不断地扩充和完善其内容和功能.该平台的成功研发,是数学机械化思想的一次成功尝试.该平台为各行各业的科研人员、工程技术人员和学生分享最新科研成果,讨论问题和交流合作等提供了便利.

当前计算平台Emathema还存在一些不足之处,后续我们将继续完善和扩充其功能,特别进行以下两方面改进∶第一,扩展Emathema的功能,尝试嵌入一些Maxima及Mathematica外部应用软件;第二,优化Emathema的界面,尝试在输入页面增加代码高亮、关键字自动补全、代码折叠展开等功能.

[1]WANG P,GRAY S,KAJLER N,et al.IAMC architecture and prototyping:A progress report[C]//Proceedings of the 2001 International Symposium on Symbolic and Algebraic Computation.ACM,2001:337-344.

[2]Wolfram Research Inc.webMathematica[EB/OL].(2002-06-18)[2016-09-15].http://www.wolfram.com/ products/webmathematica/.

[3]P´EREZ F,GRANGER B E.IPython:A system for interactive scientific computing[J].Computing in Science &Engineering,2007,9(3):21-29.

[4]PAU C,SCHREINER W.Distributed Mathematica[M/OL].(2000-07-01)[2016-09-15].http://www.risc.jku.at/ software/distmath/report/index.html.

[5]WU Y W,LIAO W D,WANG P,et al.An internet accessible grid computing system:Grid-Elimino [C]//Proceedings of IAMC.2003:1-8.

[6]FUJIMOTO M,SUZUKI M.AsirPad—a computer algebra system with a pen-based interface on PDA [C]//Proceedings of 7th Asian Symposium on Computer Mathematics(ASCM2005).Korea Institute for Advanced Study,2005:259-262.

[7]HOY M B.Wolfram|Alpha:A brief introduction[J].Medical Reference Services Quarterly,2010,29(1):67-74.

[8]MELIS E,ANDR`ES E,B¨UDENBENDER J,et al.ActiveMath:A generic and adaptive web-based learning environment[J].International Journal of Artif i cial Intelligence in Education(IJAIED),2001,12:385-407.

[9]Maplesoft Inc.Maple TA[EB/OL].(2003-04-03)[2016-09-10].http://www.maplesoft.com.cn/products/mapleta/.

[10]AL-SHOMRANI S,WANG P.DMAS:A web-based distributed mathematics assessment system[C]//Proceedings of the International Conference on Learning.2008:3-6.

[11]YANG L,SU W,WANG K J,et al.iMathema:A novel online intelligent computing system oriented to common scientific computations[C]//Proceedings of the Second International Conference on Innovative Computing and Cloud Computing.ACM,2013:10-16.

[12]POLYANIN A D.EqWorld(The World of Mathematical Equations)[EB/OL].(2004-04-12)[2016-09-01]. http://eqworld.ipmnet.ru.

[13]Equation Sheet.com[EB/OL].(2007-04-23)[2016-09-10].http://equationsheet.com/sheets/Equations-13.html.

[14]Oxford Centre for Nonlinear Partial differential Equations.OxPDE[EB/OL].(2007-05-10)[2016-09-03]. http://www.maths.ox.ac.uk/groups/oxpde.

[15]华东师范大学偏微分方程中心[EB/OL].(2010-09-05)[2016-09-01].http://www.cpde.ecnu.edu.cn/.

[16]The PHP Group.PHP:Hypertext preprocessor[EB/OL].(2001-05-13)[2016-09-01].http://php.net.

[17]W3C Recommendation.Mathematical Markup Language(MathML)version 3[EB/OL].(2010-10-20)[2016-09-01].http://www.w3.org/TR/MathML3/.

[18]GRAY J.ASCIIMathML:Now everyone can type MathML[J].MSOR Connections,2007,7(3):26-30.

[19]CERVONE D.MathJax:A platform for mathematics on the Web[J].Notices of the AMS,2012,59(2):312-316.

[20]ASLESON R,SCHUTTA N T.Foundations of Ajax[M].Berkeley:Apress Press.2005.

[21]jQuery main website.jQuery:The write less,do more,Javascript library[EB/OL].(2009-05-10)[2016-09-02]. http://jquery.com/.

[22]LI Z B,LIU Y P.RATH:A Maple package for f i nding travelling solitary wave solutions to nonlinear evolution equations[J].Computer Physics Communications,2002,148(2):256-266.

[23]LI Z B,LIU Y P.RAEEM:A Maple package for f i nding a series of exact traveling wave solutions for nonlinear evolution equation[J].Computer Physics Communications,2004,163(3):191-201.

[24]LI Z B,LIU Y P,QIAN H F.A method and its implementation for constructing B¨acklund transformations to nonlinear evolution equations[J].Computer Mathematics,2008:188-198.

[25]LIN Y Z,LI Z B,LIU Y P.Symbolic computation of analytic approximate solutions for nonlinear fractional differential equations[J].Computer Physics Communications,2013,184(1):130-141.

[26]WANG D M.An implementation of the characteristic set method in Maple[M]//Automated Practical Reasoning. Wien:Springer-Verlag,1995:187-201.

[27]WANG D M.Epsilon:A library of software tools for polynomial elimination[J].Mathematical Software,2002: 379-389.

[28]WANG D K.Wsolve:A Maple package for solving system of polynomial equations[EB/OL].(2004-05-10)[2016-09-04].http://www.mmrc.iss.ac.cn/dwang/wsolve.html.

[29]LIU Y P,YAO R X,LI Z B,et al.An online computing and knowledge platform for differential equations [C]//Proceedings of the 5th International Congress on Mathematical Software.Springer International Publishing, 2016:181-188.

(责任编辑：林磊)

Emathema:An online automated computing platform for equations

YANG Le,LIU Yin-ping,LI Zhi-bin
(Department of Computer Science and Technology,East China Normal University,Shanghai200062,China)

differential equations are playing more and more important role in modern science and technologies,engineering.On solving and integrability analysis of differential equations,our research group developed a dozen different of f-line related software based on Maple.On the basis of these Maple packages,Maple and some open-source technologies, an online automated computing platform for equations called Emathema was proposed and implemented.Emathema can provide convenient and efficient online computing and graphing services for users.On this platform,users can not only solve nonlinear algebraic and differential equations using external Maple packages,but also execute almost all simple symbolic computations related to equations in the interactive mode.For each input, Emathema outputs the computing result visually.

symbolic computation;online computing platform;Maple package; differential equation

O175;TP311.5;TH123+.1

A

10.3969/j.issn.1000-5641.2017.03.002

1000-5641(2017)03-0020-09

2016-09-28

国家自然科学基金(11435005)

杨乐,男,硕士研究生,研究方向为计算机符号计算及其应用. E-mail：yangle20081982@163.com.

柳银萍,女,教授,研究方向为符号计算、数学机械化.E-mail：ypliu@cs.ecnu.edu.cn.