基于串联制动电阻的生物质能同步发电机组低电压穿越研究

李生虎，安 锐，孙 琪

（合肥工业大学 电气与自动化工程学院，安徽 合肥 230009）

0 引言

生物质能发电利用农业、林业和工业废物、垃圾为原料，与风能、太阳能同属可再生能源。与风电、光伏采用变流器并网不同，生物质能发电多采用同步发电机（SG）并网，随机性较弱，可控程度和电能质量稍好［1］。

新能源接入影响电网有功平衡和暂态稳定［2-3］，同时对其有低电压穿越（LVRT）要求。目前风电机组（WTG）的 LVRT研究成果很多，如文献［4-6］研究了利用串联制动电阻（SBR）实现感应风电机组LVRT，给出SBR投切判据，仿真选取SBR阻值；文献［7-9］采用转子或直流侧撬棒保证双馈感应风电机组或直驱永磁同步机组不脱网运行。

但是并网标准并不局限于风电和光伏，同样适用于SG。德国在2008年提出中压并网导则［10-11］，其中直接并网SG被定义为第1类机组，同样要满足LVRT准则。SG与电网间不存在缓冲电力电子设备，功角摇摆后果远比过电流严重，需优先考虑。但现有SG研究多忽略LVRT，原因在于：大型水、火电厂中，SG惯性较大［12］，即使第一摆失稳，时间也长达零点几到几秒，一般可以满足LVRT准则；大型电网紧急控制措施（ECMs）非常完备，如电气制动、快关（调）汽门、低频/低压减载等，可以最大限度维持SG不脱网。

生物质能发电厂（BPP）中SG容量和惯性较小，外部故障后容易失稳。出于成本考虑，其ECMs远没有大型SG完备。其LVRT问题与风电机组不相同，即便是风电机组，不同类型的机组LVRT面临的问题也不同。鼠笼式感应发电机（IG）面临的是滑差失稳问题；双馈感应发电机（DFIG）面临的是转子变流器过电流和直流母线过电压问题；直驱永磁同步发电机组（PMSG）面临的是直流母线过电压问题；而SG面临的是功角失稳问题。不同类型的机组对应于不同的失稳方式，相关的约束条件不同，不能将WTG的LVRT措施直接移植到SG，因此迫切需要研究SG的LVRT特性。然而目前国内外相关研究极少，只有文献［13］检验了SG是否满足LVRT准则，讨论了采用SBR实现LVRT的可行性，但未仿真验证，也未给出SBR取值算法。

针对SG功角稳定问题，Xyngi研究了故障距离的影响［14］；Calderaro分析了SG脱网后暂态过程对线路保护的影响［15］；Razzaghi仿真了不同系统参数和故障形式对临界切除时间（CCT）的影响，用于脱网判据整定［16］；Kalyani仿真了SG不同阶数模型的暂态稳定性［17］。上述文献均基于时域仿真算法。采用能量函数（EF）法，文献［18-20］建立 SG 二阶模型，Sun 利用哈密顿定则建立SG三阶模型［21］，用以分析暂态稳定性。上述文献只计算CCT，确定脱网判据，未提出LVRT措施；而时域仿真和能量函数方法也未直接确定LVRT参数。另外，二阶模型得到的稳定结果误差较大；三阶模型计及励磁绕组动态，但未考虑励磁控制。

针对BPP中SG暂态稳定性，本文采用SBR实现LVRT，首次提出计及励磁系统动态控制的等面积定则，推导SBR阻值解析算法。基于SG及励磁系统，量化SBR功率，将其引入SG加速面积，建立加速和减速面积表达式。结合机械功率、切入功角，利用等面积定则确定满足LVRT准则SBR最小阻值。改变系统参数，分析其对SBR最小阻值的影响，对新安装BPP参数选择有参考意义。动态仿真结果验证了解析算法选取SBR阻值的正确性及LVRT的有效性。

1 故障后励磁电压时域表达

SG结构图如图1所示，其机端通过升压变压器T连接到公共连接点（PCC）。当SG正常运行时，开关闭合，旁路SBR；当满足投入判据时，开关断开，串入SBR以提高机端电压，减小功角摇摆，使得SG满足LVRT准则，维持并网。

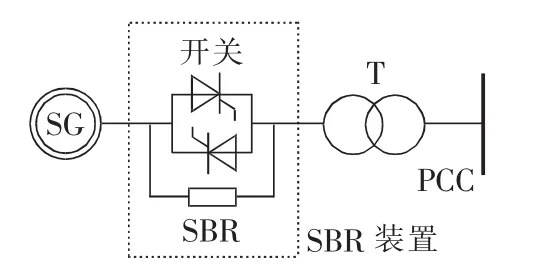
图1 SBR接入同步发电机Fig.1 SG with SBR

SG的三阶模型方程如下：

其中，Xd∑=Xd+XT；Xq∑=Xq+XT；X′d∑=X′d+XT；δ、ωr、TJ、Pm、Pe、D 分别为功角、角速度、惯性时间常数、机械功率、电磁功率和阻尼系数；T′d0、E′q、UPCC、Xd、Xq、X′d、XT、Ef分别为d轴暂态时间常数、q轴暂态电动势、PCC电压、d轴同步电抗、q轴同步电抗、d轴暂态电抗、变电压电抗和励磁电压。Pe定义为：

基于 IEEE STA1 模型［22］，励磁模型见图2。其中，TB、TC为滞后环节时间常数；TA、KA分别为放大环节时间常数和放大倍数；UI为滞后环节后的输出值；Efp为放大环节输出的励磁电压；Ef0为励磁电压初值；Efmax、Efmin分别为励磁电压上限值和下限值；Uref为PCC电压参考值；s为拉氏算子。

图2 IEEE STA1励磁模型Fig.2 IEEE STA1 excitation model

下面求解励磁电压，结合SG三阶模型，得到暂态电势表达式。励磁电压求解分为以下2种情况：当PCC电压瞬时跌落和恢复时，输入信号Uref-UPCC发生突变，通过将微分方程差分化得到；其他时刻时，输入信号Uref-UPCC保持恒定，滞后环节变为惯性环节，此时可以得到其时域表达式。

在电压跌落期间（除了跌落瞬间），有：

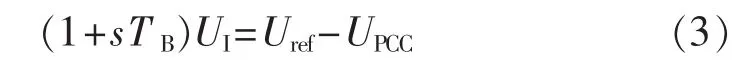
求解式（3）一阶微分方程，得到：

其中，c1=UI（t0+Δt）-（Uref-UPCC），t0为故障初始时刻，Δt为仿真步长；t为时间。将式（4）代入放大环节得：

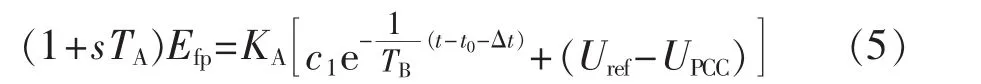
求解式（5）一阶微分方程，得到：

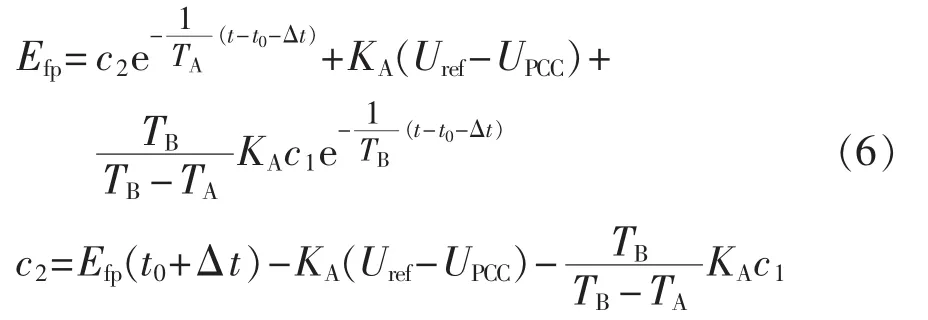
当PCC电压跌落至0时，重写式（1）中第3个方程，得到：

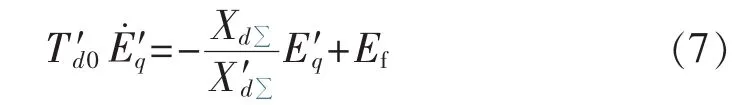
求解式（7）微分方程得到E′q。分为以下2种情况：当 Ef小于励磁电压上限值 Efmax时，E′q如式（8）所示；当 Ef达到 Efmax时，E′q如式（9）所示。

其中，c4=E′q（t0′）-EfmaxX′d∑/Xd∑，t0′为故障后励磁电压恰好为最大值时对应的时刻。

在电压恢复后（除了恢复瞬间），方程为：

求解式（10）一阶微分方程，得到：

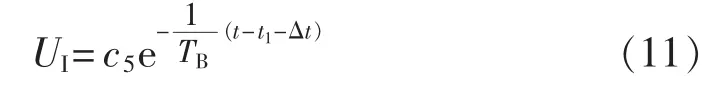
其中，c5=UI（t1+Δt），t1为故障清除时刻。

当 UI≥（Efmax-Ef0）/KA时，励磁电压受其上限值限制，此时 Ef=Efmax。当 UI＜（Efmax-Ef0） /KA时，励磁电压小于其上限值，将式（11）代入放大环节，得到Efp为：

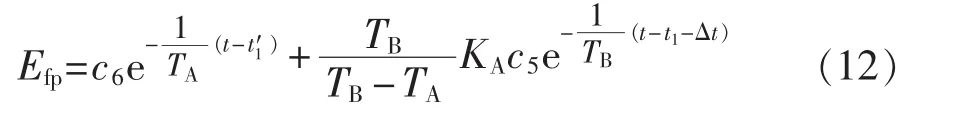
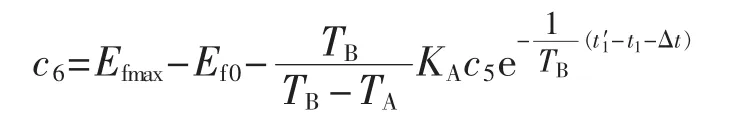
其中，t1′为故障后 UI=（Efmax-Ef0）/KA的时刻。根据上述推导发现，Ef与调节参数和电压跌落深度有关，Eq′ 变化受 Efmax制约。

2 SBR投切判据及阻值选取

SG失稳与故障前机械功率Pm和故障后电压跌落深度有关，不同Pm对应不同临界电压UPCCcr。在SG不失稳时投入SBR，不利于故障期间有功输出；而SG可能失稳时不投入SBR，不能实现LVRT。

针对不同Pm，计算对应的临界电压。检测Pm和UPCC，当UPCC小于对应UPCCcr时，同时为了防止SBR反复投切，需满足功角大于切入功角δc才投入SBR。由于SG切入功角表明其已快达到失稳的状态，所需SBR阻值很大。很可能需要电网倒送功率，不利于维持电网频率，所以不能直接确定切入功角取值。通过改变切入功角值分析SBR阻值的变化，以确定切入功角范围。反之SG在并网导则规定时间内不会发生功角失稳。当PCC电压恢复正常值时，SBR切出运行。

令流经SBR的电流为IL，用暂态电势确定IL：

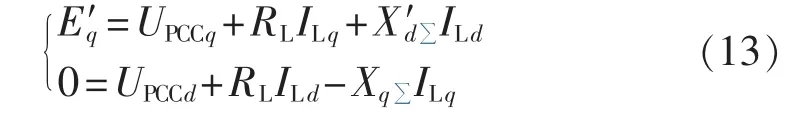
其中，下标d、q分别表示d、q轴参数；忽略定子电阻和变压器电阻时，暂态电势到PCC的电阻之和，即为SBR阻值RL。

由于RL远小于Xq∑，且当PCC电压跌落至0时得到 IL≈ E′q/X′d∑。故障期间 SBR 消耗功率 PSBR=IL2RL，会带来散热问题。阻值越大，对LVRT越有利，但不利于有功输出，所以需要确定SBR最小阻值。

SBR最小阻值确定是以传统的等面积定则为基础，对其进行了部分改进。SBR的作用是减缓SG功角的增加速度，最终使功角不达到其不平衡点。将PSBR引入加速面积中，对加速面积的影响如下：当达到切入功角时投入SBR，故障清除后切出SBR，减小了此时刻内的加速面积。而SBR未投入时的加速面积和SBR切出运行的减速面积与传统的加速面积和减速面积保持一致。由于考虑励磁系统动态控制时，次暂态电动势的变化导致式（2）有功功率的正弦函数幅值和功角不平衡点的变化，不能直接通过求解加速面积和减速面积表达式确定SG是否失稳。

加速面积和减速面积表达式的建立采用积分的思想，将每次迭代产生的功率差与功角差的乘积相加，所以需要确定功率差和功角差。在第1节已得到Ef以及故障期间的E′q，将其代入SG及其励磁系统，此时原有的五阶微分方程在故障期间转化为仅包含δ和ωr为状态变量的二阶微分方程，在故障恢复后转化为仅包含δ、ωr以及E′q为状态变量的三阶微分方程。但是SG功角和转速相互耦合，仍然很难得到解析解。采用微分方程的数值解法，求解故障期间的二阶微分方程、故障恢复后的三阶微分方程，得到功角差和功率差，将其代入加速面积和减速面积表达式中。

当t0＜t≤t1时加速面积由两部分组成：Sa=Sa1+Sa2。当δ＜δc时SBR未投入，加速面积Sa1为：

其中，下标n和n+1分别表示第n次和第n+1次迭代。

当δ≥δc时SBR已投入，加速面积Sa2为：

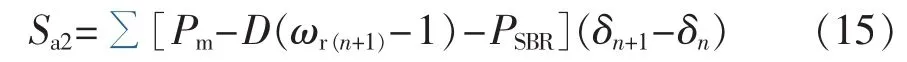
功角不稳定平衡点δh与故障后的E′q有关，通过如下功率平衡关系求解。

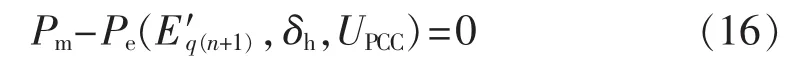
当 t＞t1且 δ＜δh时减速面积 Sb为：

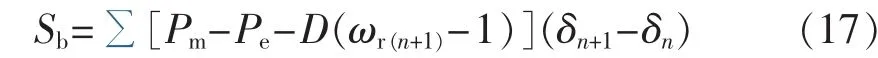
根据式（14）—（17）确定了加速面积和减速面积，由等面积定则可知：当Sa＞Sb时，SG功角失稳；当Sa=Sb时，SG处于临界稳定；当Sa＜Sb时，SG保持功角稳定。将SBR阻值由0开始逐渐增大，比较Sa和Sb大小。当恰好满足Sa＜Sb时，对应的SBR阻值即为其最小值。SBR最小阻值确定方法是基于计及励磁系统的动态调节过程等面积定则，其励磁电压和q轴暂态电势经过严格的公式推导，等面积定则又是由改进欧拉法求解建立，所以该方法是通用的。

故障期间SBR是否需要从电网吸收有功，由故障发生时Pm和SBR阻值决定。当SBR消耗的功率PSBR恰好为机械功率Pm时，得到SBR临界阻值：

当SBR阻值大于RLcr时，需要电网倒送功率以满足SBR消耗的功率。

本文选取文献［10］规定的LVRT标准，PCC电压跌落至0长达150 ms。当SG额定运行时电磁功率最大，故障期间SG不平衡功率最大，功角加速最快，失稳时间最短。选取SG为额定运行时的SBR阻值可以满足各种运行条件的LVRT要求。

3 仿真验证与分析

SG 参数为［23］：TJ=1.4 s，Xd=2.06 p.u.，Xq=2.5 p.u.，X′d=0.398 p.u.，漏抗 Xl=0.1 p.u.，T′d0=7.8 s。变压器电抗XT=0.1 p.u.。励磁系统参数为：KA=150，TA=0.01 s，TB=0.2 s，TC=0.1 s，Efmax=5 p.u.。仿真步长 Δt=0.001 s。

3.1 SBR阻值计算

表1给出了δc=52.4°、不同SBR阻值时采用解析算法得到的加速面积与减速面积（表中数值均为标幺值）。可以看出SBR阻值越大，加速面积越小，减速面积先增大再减小，SG越容易保持稳定。当RL较小时，制动电阻消耗功率较小，功角加速过快，SG容易失稳。当RL为0.09 p.u.时，恰好满足Sa＜Sb，即SG功角在三相故障150ms时不会发生功角失稳，显然SBR阻值最小值为0.09 p.u.。

图3表示切入功角与SBR阻值的关系（RL为标幺值）。可以看出切入功角越大，SBR阻值及其变化率越大，SG越难实现LVRT。这是由于SBR未投入时，加速功率几乎等于机械功率，功角加速最快。切入功角越大，加速面积越大，而减速面积不变，需要更大阻值的SBR减小余下故障时间内的加速面积。由式（18）得到SBR的临界阻值为0.16 p.u.，对应的临界切入功角为74°。即当切入功角小于74°时，SBR不需要电网倒送功率实现LVRT；反之，需要从电网吸收功率，不利于维持故障期间的电网频率。

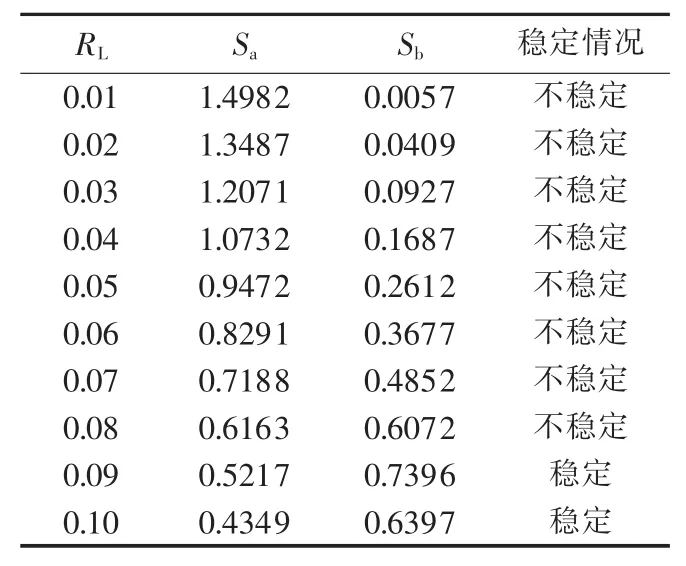
表1 不同SBR时加速面积与减速面积Table 1 Accelerating and decelerating areas for different SBRs

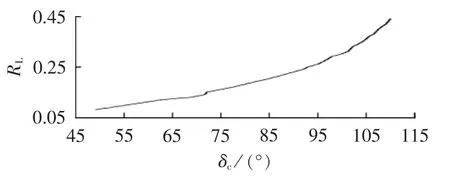
图3 SBR最小阻值与切入功角的关系Fig.3 Curve of minimum SBR vs.switch-in rotor angle

图4给出了SBR切入判据曲线（UPCCcr和Pm均为标幺值）。可以看出，当Pm小于0.63p.u.时，PCC临界电压为0，SG不需要附加措施即可实现LVRT；当Pm大于0.63 p.u.时，机械功率与PCC临界电压近似为线性关系，在额定功率时临界电压约为0.16 p.u.。机械功率越大，临界电压越高，SG越难实现LVRT。当检测到机械功率和PCC电压位于此曲线上方时，SG自身可以实现LVRT，不需要投入SBR。

图4 SBR切入判据Fig.4 Switch-in criterion of SBR

为了验证提出的计及励磁系统动态过程的等面积定则选取SBR阻值的正确性。同样令δc=52.4°，分别取RL为0.08 p.u.、0.09 p.u.，通过动态仿真得到功角变化曲线如图5 所示（UI、Ef、E′q均为标幺值）。显然当RL为0.09 p.u.时，SG可以保持功角稳定，可实现LVRT。与解析算法得到的SBR阻值一致，这是因为误差主要是由IL引起，并且基于解析算法求解得到的IL与实际值相差较小。故障瞬间由于输入信号Uref-UPCC突变，经滞后环节后输出值UI阶跃上升，而后滞后环节变为惯性环节，UI按指数函数增大。Ef迅速达到其最大值Efmax，Eq′基本维持不变。故障恢复瞬间同样由于输入信号Uref-UPCC突变，经滞后环节输出值UI阶跃下降，而后滞后环节变为惯性环节，UI按指数函数减小。由于故障恢复后一段时间内UI仍较大，Ef仍维持在最大值的时长约1 s。Eq′先减小再增大，功角振荡5 s后逐渐稳定。

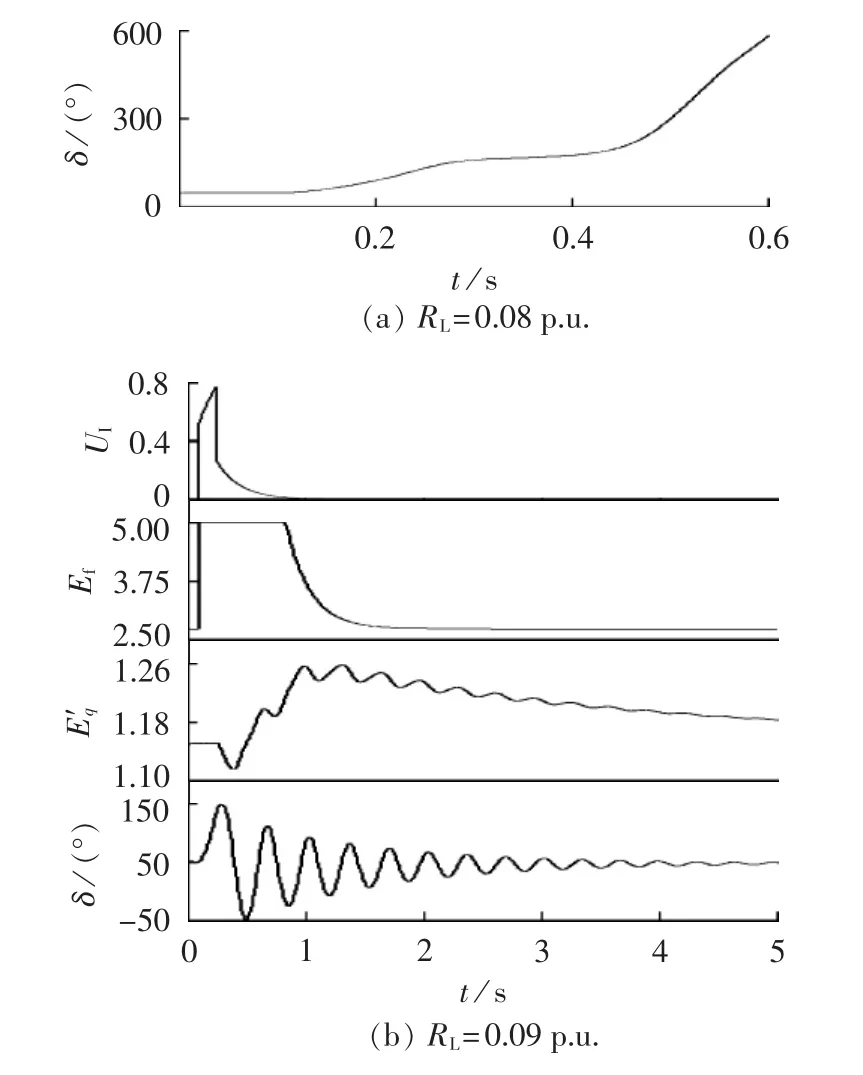
图5 不同SBR时SG稳定情况Fig.5 Stability conditions of SG for different SBRs

3.2 不同系统参数对SBR最小阻值的影响

分别改变不同的系统参数（励磁电压上限值、惯性时间常数、q轴同步电抗、d轴暂态电抗、变压器电抗），使SBR最小阻值由0.09 p.u.减小到0.07 p.u.，动态仿真得到的功角变化曲线如图6所示。需要说明的是：前述的等面积定则同样适用于研究参数变化时SG的功角稳定性。此处为了更加直观地表明SG参数对其功角稳定性的影响，采用动态仿真绘制功角变化曲线。

与原参数对比，可以看出励磁电压上限值越大，暂态电动势越大，故障恢复后电磁功率越大，减速面积越大，需要的SBR阻值越小。

惯性时间常数越大，转子和功角加速越慢，相同故障时功角失稳所需时间越长，较小阻值的SBR即可实现LVRT。

q轴同步电抗、d轴暂态电抗以及变压器电抗影响故障恢复后的电磁功率，进而影响减速面积。三者的值越小，故障后电磁功率值越大，减速面积越大，需要的SBR阻值越小。

比较而言，系统参数对SBR阻值的影响从大到小依次为：d轴暂态电抗、惯性时间常数、q轴同步电抗、变压器电抗、励磁电压上限值。

此部分得到的结论与基于等面积定则获得的SBR最小阻值之间并不矛盾，两者相互独立。解释如下：发电机组参数对SBR最小阻值的影响是动态仿真得到功角变化，通过改变不同的系统参数使得所需要的SBR最小阻值由0.09 p.u.减小到0.07 p.u.，对于新安装BPP参数选择有参考意义。而基于等面积定则得到SBR最小阻值的解析算法，是针对原始参数的解析算法，目的是在保证选取SBR阻值精度的同时节省动态仿真时间，对应的SBR最小阻值为0.09p.u.。图5是对解析算法SBR最小阻值选取正确性的动态仿真验证。

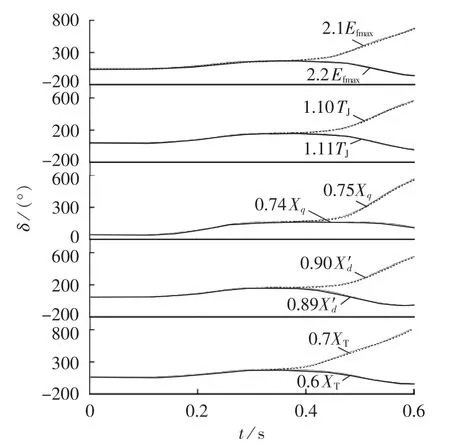
图6 不同参数对SBR阻值的影响Fig.6 Effect on SBR for different parameters

4 结论

本文采用SBR实现BPP中SG的LVRT，首次提出计及励磁系统动态控制的等面积定则，确定SBR最小阻值的解析算法，得到如下结论。

a.SG的功角稳定性与机械功率和PCC电压跌落深度有关。机械功率越大，PCC临界电压越高，相同电压跌落深度下SG越容易失稳。

b.切入功角越大，SBR阻值和阻值变化率越大。切入功角大于其临界值时，需要电网倒送功率。

c.SG惯性时间常数或励磁电压上限值越大，q轴同步电抗、d轴暂态电抗或变压器电抗越小，LVRT需要的SBR阻值越小。

d.系统参数对SBR阻值的影响从大到小依次为：d轴暂态电抗、惯性时间常数、q轴同步电抗、变压器电抗、励磁电压上限值。

［1］严鑫，吴明锋.生物质发电及能源化综合利用［J］.山西电力，2014（6）：52-55.YAN Xin，WU Mingfeng.Biomass power generation and comprehensive energy utilization［J］.Shanxi Electric Power，2014（6）：52-55.

［2］谭会征，李永丽，陈晓龙，等.带低电压穿越特性的逆变型分布式电源对配电网短路电流的影响［J］.电力自动化设备，2015，35（8）：31-37.TAN Huizheng，LI Yongli，CHEN Xiaolong，et al.Influence of inverter-interfaced distributed generatorwith low-voltage ridethrough capability on short circuit current of distribution network［J］.Electric Power Automation Equipment，2015，35（8）：31-37.

［3］赵卓立，杨苹，蔡泽祥，等.含风电孤立中压微电网暂态电压稳定协同控制策略［J］.电力自动化设备，2015，35（10）：1-9.ZHAO Zhuoli，YANG Ping，CAI Zexiang，etal.Cooperative control of transient voltage stability for islanded medium-voltage microgrid with wind power［J］.Electric Power Automation Equipment，2015，35（10）：1-9.

［4］王虹富，林国庆，邱家驹，等.利用串联制动电阻提高风电场低电压穿越能力［J］.电力系统自动化，2008，32（18）：81-85.WANG Hongfu，LIN Guoqing，QIU Jiaju，et al.Improvement of low voltage ride-through capability of wind farms by use of series dynamic braking resistors［J］.Automation of Electric Power Systems，2008，32（18）：81-85.

［5］汤凡，刘天琪，李兴源.通过串联制动电阻改善恒速异步发电机风电场暂态稳定性［J］.电网技术，2010，34（4）：163-167.TANG Fan，LIU Tianqi，LI Xingyuan.Improving transient stability ofwind farm consisting offixed speed induction generatorby series connected dynamic braking resistors［J］.Power System Technology，2010，34（4）：163-167.

［6］MUYEEN S M.A combined approach of using an SDBR and a STATCOM to enhance the stability of a wind farm［J］.IEEE System Journal，2015，9（3）：922-932.

［7］栗然，王倩，卢云，等.Crowbar阻值对双馈感应发电机低电压穿越特性的影响［J］.电力自动化设备，2014，34（4）：101-107.LI Ran，WANG Qian，LU Yun，et al.Impact of Crowbar resistance on low voltage ride through of DFIG［J］.Electric Power Automation Equipment，2014，34（4）：101-107.

［8］李生虎，许志峰.直驱永磁同步电机卸荷电阻取值范围及分组策略［J］.电网技术，2013，37（7）：1868-1873.LI Shenghu，XU Zhifeng.Range and group strategy of dump resistance for direct-drive permanent magnet synchronous generators［J］.Power System Technology，2013，37（7）：1868-1873.

［9］李生虎，安锐，许志峰，等.混合风电场中PMSG协助感应发电机低电压穿越［J］.电力自动化设备，2015，35（2）：21-27.LI Shenghu，AN Rui，XU Zhifeng，et al.Coordinated LVRT of IG and PMSG in hybrid wind farm［J］.Electric Power Automa-tion Equipment，2015，35（2）：21-27.

［10］BDEW.Technical guideline：generating plants connected to the medium-voltage network［S］.Berlin，Germany：BDEW，2008.

［11］鲍薇，胡学浩，何国庆，等.分布式电源并网标准研究［J］.电网技术，2012，36（11）：46-52.BAO Wei，HU Xuehao，HE Guoqing，et al.Study on standard for grid-integration of distributed resources［J］.Power System Technology，2012，36（11）：46-52.

［12］LI S.Effect of rotor speed change on electromagnetic transient and angular swing of synchronous generators［J］.Electric Power Components and Systems，2012，40（13）：1486-1500.

［13］YANG S，SHAGAR V G，UKIL A，et al.Evaluation of low voltage ride-through capability of synchronous generator connected to a grid［C］∥IEEE Power and Energy Society General Meeting.Denver，USA：IEEE，2015：1-5.

［14］XYNGI I，ISHCHENKO A，POPOV M，et al.Transient stability of a distribution network with distribute generators［J］.IEEE Transactions on Power Systems，2009，24（2）：1102-1104.

［15］CALDERARO A，MILAN OVIC J V，KAYIKCI M，et al.The impactofdistributed synchronousgeneratorson quality of electricity supply and transient stability of real distribution network［J］.Electric Power Systems Research，2009，79（1）：134-143.

［16］RAZZAGHI R，DAVARPANAH M，SANAYE-PASAND M.A novelprotective scheme to protectsmall-scale synchronous generators against transient instability［J］.IEEE Transactions on Industrial Electronics，2013，60（4）：1659-1667.

［17］KALYANIS，PRAKASH M，EZHILARASIG A.Transient stability studies in SMIB system with detailed machine models［C］∥InternationalConference on RecentAdvancements in Electrical，Electronics and Control Engineering.Sivakasi，India：IEEE，2011：459-464.

［18］BASLER M J，SCHAEFER R C.Understanding power-system stability［J］.IEEE Transactions on Industry Applications，2008，44（2）：463-474.

［19］PAUDYAL S，RAMAKRISHNA G，SACHDEV M S.Application of equal area criterion conditions in the time domain for outof-step protection［J］.IEEE Transactions on Power Delivery，2010，25（2）：600-609.

［20］CHOWDHURY M A，HOSSEINZADEH N，SHEN W X，et al.Comparative study on fault responses of synchronous generators and wind turbine generatorsusing transientstability index based on transient energy function［J］.International Journal of Electrical Power&Energy Systems，2013，51（10）：145-152.

［21］SUN Y，LI X，ZHAO M，etal.New Lyapunov function for transient stability analysis and control of power systems with excitation control［J］.Electric Power Systems Research，2001，57（2）：123-131.

［22］IEEE PES.Recommended practice for excitation system models for power systems stability analysis：IEEE Std 421.5-2005［S］.New York，USA：IEEE Press，2006.

［23］SALIM R H，RAMOS R A.A model-based approach for smallsignalstability assessmentofunbalanced powersystems［J］.IEEE Transactions on Power Systems，2012，27（4）：2006-2014.