基于数值模拟的覆冰导线局部对流换热分析

程丹，穆靖宇，曹雯，陈小改，朱永灿

（1.西安工程大学电子信息学院，陕西西安 710048；2.国网安徽电力公司检修公司，安徽合肥 230601）

基于数值模拟的覆冰导线局部对流换热分析

程丹1，穆靖宇2，曹雯1，陈小改1，朱永灿1

（1.西安工程大学电子信息学院，陕西西安 710048；2.国网安徽电力公司检修公司，安徽合肥 230601）

覆冰事故是影响输电线路正常运行的重要原因。对输电线路覆冰过程中各热平衡影响因素进行分析，得出对流换热为该过程最重要的热损耗原因。针对对流换热、导线焦耳热两大影响因素开展数值模拟，得出雨凇覆冰导线的热量损失随风速及冰厚增加而增加，偏心圆形覆冰对流换热数值略小于圆形覆冰。对覆冰表面各部分的热量损失进行统计，结果表明，当风速小于10 m/s、覆冰厚度小于5 mm时，LGJ95导线迎风侧-45～45°区域的热耗散值达到了总量的35%～48%，热量散失远大于平均值，有利于覆冰冻结增长。

覆冰导线；对流换热；热平衡；冰层温度；数值模拟

我国幅员辽阔，线路走廊多跨越高山、沟谷，受微地形、微气象条件影响，输电线路冰灾事故频繁发生，造成严重经济损失。而覆冰生长过程非常复杂，空气温度、湿度、风速、风向、液滴颗粒大小、导线自身特性等都对覆冰发展有重要影响，建立完善的覆冰模型是非常困难的[1]。

国内外学者基于气象学、流体力学、热力学等开展了大量输电线路覆冰机理研究[2-3]。文献[4]将覆冰生长分解为过冷却液滴的碰撞、捕获、冻结过程，对应于碰撞率a1、结合率a2和冻结率a3。文献[5]进行风洞实验，监测单位时间内围绕导线的雪花分量、风速、湿度、温度，分析各种气象参数对冰雪密度和积雪效率的影响。文献[6-7]设计了基于力学模型的输电线路覆冰监测系统，并通过灰色理论量化各气象参数、导线温度对覆冰生长的影响。这些研究大都没有考虑导线运行温度（电流）对覆冰的影响，但实际上导线运行温度对覆冰过程影响很大。文献[8]测算了不同参数导线表面的换热系数。文献[9-10]在导线表面焦耳热、传导热和辐射热等因素基础上推导导线临界防冰电流、融冰时间等参数。但这些研究都将导线作为一个整体，从宏观上对覆冰过程进行分析和模拟，缺乏覆冰生长过程中冰层局部热平衡以及导线覆冰层对热平衡的影响分析。

1 覆冰导线热平衡方程

如图1所示，在覆冰、融冰过程中，导线焦耳热通过冰层传导到冰面，再由冰面散失到空气中。单位长度覆冰导线表面的热平衡可通过式（1）表示[11-13]：

式中：Qci为单位长度导线传导到覆冰表层的热量；Qcq为对流换热损失；Qe为覆冰表面蒸发/升华产生的热损失；Qs为辐射产生的热损失；Ql为碰撞、附着到导线的过冷却水滴升温、相变引起的热量变化，Qn为日光短波加热、空气摩擦对冰面加热等微小因素的总和，其值一般较小，忽略其对热平衡的影响。

图1 导线冰层热平衡示意Fig.1 The thermal equilibrium in the ice sleeve accumulated on conductor

在标准大气压下，假设导线温度tc=0℃（273.15 K），空气温度tf=-3℃，a1=0.7，a2=1，a3=1，ω=1 g/m3，忽略其他微小值，单位长度LGJ95导线（直径D=13.61 mm）表面热量散失值如图2所示。

随着流场内风速的增加，导线表面对流换热Qcq、蒸发/升华吸热Qe以及过冷却液滴升温、冻结所对应的热量损失值Ql都呈现近似线性增长。但Ql及Qs数值都较小，可忽略其对热平衡的影响。在温度为-10～0℃时，可认为饱和蒸汽压与温度值近似呈线性关系，有Qcq≈k1Qe=f（Acq，h，tiw，tf）成立，其中Acq为单位长度覆冰导线表面积；h是对流换热系数；tiw和tf分别为冰面温度和环境温度。因此通过对Qcq分析即可反映出导线表面热量损失。

图2 单位长度LGJ95导线各因素散热值Fig.2 Different heat loss values for the LGJ95 conductor of the unit length

2 覆冰导线对流换热数值模拟

2.1 圆形覆冰导线对流换热的数值模拟

如图3所示，设置导线直径13.61 mm（简化为圆柱形），冰层厚度5 mm，风速10 m/s，导线温度tc=0℃，tf=-3℃。覆冰层为雨凇，热导率取2.2 W/（m·K），远低于铝。在气流作用下，冰层表面局部对流换热数值和温度差异很大，覆冰层形成明显的温度梯度，随着流场雷诺数的增加，冰层温度梯度随之增加。

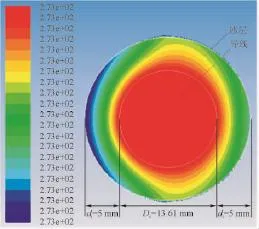
图3 导线覆冰层温度梯度Fig.3 Temperature distribution in iced conductor

冰层表面温度及对流换热系数分布曲线如图4所示，导线表面平均对流换热系数h为76 W/（m2·K），而迎风侧驻点处的h为127 W/（m2·K）。受此影响，冰层表面平均温度为-0.53℃，而迎风侧驻点处的温度为-0.79℃，冰层表面温度及对流换热系数随迎风角度的不同差异非常明显。

采用数值模拟得到的单位长度覆冰导线对流换热Qcq如图5所示。为了分析覆冰前后冰层单位面积对流换热数值的差别，定义冰层表面平均热流密度：

式中：Acq为单位长度覆冰导线的表面积，对于直径为di的圆形覆冰导线，Acq=2π（Rc+di）。覆冰导线随风速变化的曲线如图6所示，在风速1～10 m/s条件下，随着导线覆冰层厚度增加，冰层减小，但覆冰厚度的增加使散热面积Acq增大，覆冰导线总的对流换热值Qcq仍然缓慢增大。因此在雨凇融冰工程中，最小融冰电流随覆冰层厚度增加而增加。

图4 圆形覆冰表面温度及对流换热系数分布Fig.4 Temperature and heat transfer coefficient distribution on round iced conductor surface

图5 单位长度圆形覆冰导线对流换热变化曲线Fig.5 The convective heat transfer of unit length round iced conductor

图6 圆形覆冰表面平均热流密度随风速变化曲线Fig.6 The mean heat flux of round iced conductor with wind speed

2.2 偏心圆形覆冰导线表面对流换热

受环境温度、湿度、风速、风向、液滴中值直径、导线刚度、负荷电流、气象变化等多种因素影响，导线覆冰形状是不规则的，圆形、偏心圆形、椭圆形、新月形等形状的覆冰导线非常常见。为了分析覆冰形状对表面热平衡的影响，选用图7中的偏心圆形覆冰为研究对象，设置迎风侧覆冰厚度dil=1.5di，背风侧覆冰厚度dis=0.5di。保持2.1节模拟条件不变，di=5 mm，直径13.61 mm的导线覆盖偏心覆冰后对流换热数值及温度分布如图8所示。

图7 偏心圆形覆冰层温度梯度Fig.7 Temperature distribution in eccentric ice sleeve accumulated on conductor

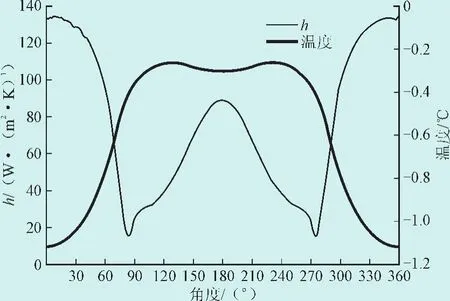
图8 偏心圆形覆冰表面温度及对流换热系数分布Fig.8 Temperature and surface heat transfer coefficient distribution on eccentric iced conductors surface

偏心圆形覆冰迎风侧冰层厚，冰层热阻大，相同条件下传导到冰层表面的热量少，局部温度更低，在风速为10 m/s时，迎风侧驻点处温度为-1.13℃；背风侧冰层厚度小，热阻低，导线的焦耳热很容易传导到冰层表面，背风侧驻点处温度为-0.32℃。由于冰层背风侧冰层薄、热阻小，虽然背风侧局部对流换热系数差异很大，但冰层表面温度值差异并不明显。偏心覆冰导线表面Qcq值如图9所示，在风速1～10 m/s范围内，偏心圆形覆冰表面Qcq值略低于圆形覆冰，当覆冰厚度为5 mm、风速为10 m/s时，相比于圆形覆冰，偏心圆形覆冰Qcq减小约6%。

图9 偏心圆形覆冰导线对流换热随风速变化曲线Fig.9 The convective heat transfer of iced conductors with different wind speed

3 覆冰导线局部对流换热

3.1 无覆冰时导线的局部对流换热

导线迎风侧对流换热数值大于背风侧，导线表面温度并不一致，有必要对导线局部的热平衡过程进行研究。相关研究表明，过冷却液滴与导线的碰撞点主要集中在迎风侧-45°～45°，当风速及过冷却液滴直径较大时，碰撞点可达到-70°～70°，但随着角度增加，过冷却液滴的局部碰撞系数快速降低，液滴的碰撞区域仍主要集中在45°范围内。因此，在以导线迎风侧驻点为起点，将导线均分为8个区段，采用局部区域平均对流换热数值作为覆冰分析依据。

钢芯铝绞线由铝丝螺旋绞合而成，表面粗糙度大于光滑圆柱。文献[14]指出粗糙圆柱表面的平均对流换热损失大于光滑圆柱，且该差异值随风速的增大而增大。由数值模拟得到的不同风速条件下LGJ95导线以及相同直径光滑圆柱各区段Qcq值如图10所示。当风速为1 m/s时，覆冰表面对流换热数值较低，LGJ95导线与光滑圆柱各区段的Qcq值基本一致。随着风速增的加，LGJ95导线及光滑圆柱表面对流换热强度都在增加，但受导线曲率影响，导线表面出现多个气流分离点，背风侧卡门涡强度增大，平均努赛尔特数增大，对流换热数值显著增加。

3.2 圆形覆冰导线局部对流换热

设置导线LGJ95表面圆形覆冰厚度1～5 mm，不同风速条件下各区段Qcq如图11所示。在风速低于5 m/s时，导线迎风侧局部对流换热值随覆冰层厚度增加而增加；而在风速10 m/s时，由于覆冰导线的阻尼作用，不同厚度覆冰导线迎风侧平均热量损失差异迅速减小，Qcq数值几乎不随冰层增加；但由于流场雷诺数增加，导线背风侧卡门漩涡强度增强，局部空气流速增大，背风侧局部对流换热随覆冰厚度增大快速增加。

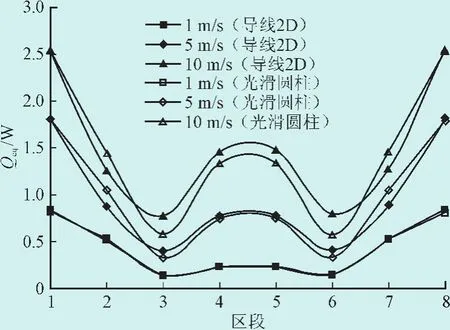
图10 无覆冰导线各区段对流换热曲线Fig.10 Local convective heat transfer of conductor

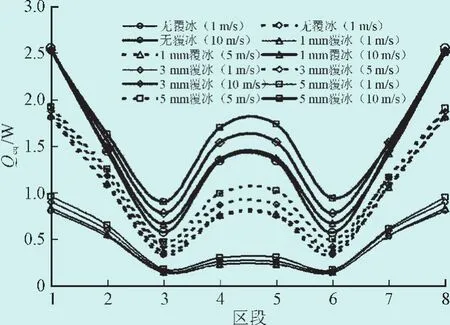
图11 圆形覆冰导线局部对流换热值Fig.11 Local convective heat transfer of round iced conductors

3.3 偏心圆形覆冰导线局部对流换热

假设LGJ95导线覆冰形状为偏心圆形，形状与2.2节一致，保持其他数值模拟条件不变，不同风速下偏心覆冰导线局部Qcq如图12所示。

在风速较高时，偏心圆形覆冰导线迎风侧平均对流换热数值小于圆形覆冰导线；但偏心圆形覆冰导线背风侧冰层薄，冰层热阻小，局部温度高，偏心圆形覆冰背风侧对流换热值大于圆形覆冰导线。在1～10 m/s风速范围内，LGJ95导线迎风侧-45～45°区域局部Qcq占总对流换热数值的比率kup如表1所示，在风速为1 m/s时，直径为13.61 mm的无覆冰光滑圆柱kup达到了48%。随着风速及覆冰厚度的增加，导线背风侧卡门涡强度增大，背风侧局部对流换热增强，kup值逐渐下降，但这些条件下的圆形和偏心圆形覆冰导线的kup分别为39.5%和35.5%，仍然远大于平均热散失。

图12 偏心圆形覆冰导线局部对流换热值Fig.12 Local convective heat transfer of eccentricity iced conductor

表1 LGJ95导线覆冰后的kup值Tab.1 Kup number of LGJ95 conductors with ice covered %

4 结语

覆冰事故是影响输电线路安全运行的重要原因，本文从覆冰导线热平衡影响因素入手，针对雨凇覆冰导线对流换热进行数值模拟，结果表明：在环境温度和导线温度一定的条件下，单位面积覆冰导线的对流换热数值随冰厚增加而下降，但由于冰层表面积的增大，雨凇覆冰导线总的对流换热数值缓慢增加；由于冰层热阻的变化，偏心圆形覆冰对流换热数值略小于圆形覆冰，覆冰形状对覆冰表面热散失存在一定影响。最后对冰层表面各部分的对流换热数值进行分区域统计，得出当风速小于10 m/s、覆冰厚度小于5 mm时，LGJ95导线覆冰层迎风侧-45～45°区域的热量散失值达到总数的35%～48%，局部热散失远大于平均数值，但随着冰层厚度的增加，该比例逐渐降低。

[1]黄新波.输电线路在线监测与故障诊断[M].北京：中国电力出版社，2008.

[2]Farzaneh.电网的大气覆冰[M].黄新波，译.北京：中国电力出版社，2010.

[3]SAVADJIEV K，FARZANEH M.Modeling of icing and ice shedding on overhead power lines based on statistical analysis of meteorological data[J].IEEE Trans.Power Delivery，2004，19（2）：715-721.

[4]MAKKONEN L，STALLABRASS J R.Experiments on the cloud droplet collision efficiency of cylinders[J].Climate Appl Meteor，1984（26）：1406-1411.

[5]MATSUSHITA T，NISHIO F.Local influence on occurrence of freezing rain and precipitation icing in Japan[C]//11th International Workshop on Atmospheric Icing of Structures（IWAIS），2005.

[6]黄新波，欧阳丽莎.输电线路覆冰关键影响因素分析[J].高电压技术，2011，37（7）：1677-1682.HUANG Xinbo，OUYANG Lisha.Analysis on key influence factor of transmission line icing[J].High Voltage Engineering，2011，37（7）：1677-1682（in Chinese）.

[7]HUANG Xinbo，LIN Shufan.Ice growth prediction model of transmission lines based on mamdani-type fuzzy neural network[C].15th International Workshop on Atmospheric Icing of Structures（IWAIS 2013），2013（3）：59-71.

[8]ZSOLT Peter.Modeling and simulation of the ice melting process on a current-carrying conductor[D].Canada：Quebec University，2006.

[9]蒋兴良，兰强.导线临界防冰电流及其影响因素分析[J].高电压技术，2012，38（5）：1225-1232.JIANG Xingling，LAN Qiang.Analysis on critical antiicing current of conductor and its impacting factors[J].High Voltage Engineering，2012，38（5）：1225-1232（in Chinese）.

[10]蒋兴良，范松海，胡建林，等.输电线路直流短路融冰的临界电流分析[J].中国电机工程学报，2010，30（1）：111-116.JIANG Xingliang，FAN Songhai.Analysis of critical icemelting current for short-circuit DC transmission line[J].Proceedings of the CSEE，2010，30（1）：111-116（in Chinese）.

[11]肖丹华.基于多相流理论的导线覆冰过程研究[D].重庆：重庆大学，2011：37-38.

[12]FARZANEH M，LAFORTE J L.Ice accretion on conduc-tors energized by AC or DC—A laboratory investigation of ice treeing[J].International Journal of Offshore and Polar Engineering，1994，4（1）：663-672.

[13]朱永灿，黄新波，贾建援，等.输电导线覆冰生长及影响因素数值分析模型[J].西安交通大学学报，2015，49（7）：120-125.ZHU Yongcan，HUANG Xinbo，JIA Jianyuan，et al.Numerical simulation of icing and influence on transmission line[J].Journal of Xi’an Jiaotong University，2015， 49（7）：120-125（in Chinese）.

[14]MAKKONEN L.Heat transfer and icing of a rough cylinder[J].Cold Regions Science and Technology，1985（10）：105-116.

Analysis of Local Convective Heat Transfer of Iced Conductor Based on Numerical Simulation

CHENG Dan1，MU Jingyu2，CAO Wen1，CHEN Xiaogai1，ZHU Yongcan1
（1.School of Electronics and Information，Xi’an Polytechnic University，Xi’an 710048，Shaanxi，China；2.Maintenance Company of State Grid Anhui Electric Power Company，Hefei 230601，Anhui，China）

Ice accident is the important factor affecting the normal operation of transmission lines.In this paper，first of all，heat balance influence factors in the icing process of transmission lines are analyzed to conclude that the convective heat transfer is the most important heat loss factor.A numerical simulation is conducted for two factors：convective heat transfer and conductor joule heat，and it is found that the heat loss of the glazed iced conductor increases with the increase of wind speed and ice thickness，and the heat convection of the eccentric circular ice is slightly smaller than that of the circular ice.Furthermore，the heat loss of each part of the ice surface is statistically analyzed，and the result shows that when the wind speed is less than 10 m/s and ice thickness is less than 5 mm，the thermal dissipation value of the windward LGJ95 in the-45～45°area reaches 35%～35%，thus the local heat loss in the windward area is much more than the mean value，which plays a positive role in icing growth.

iced conductor；convective heat transfer；thermal equilibrium；ice temperature；numerical simulation

2016-06-22。

程 丹（1986—），女，硕士，助理工程师，现从事电力设备检测技术、覆冰生长机理等研究工作。

（编辑 董小兵）

国家自然科学基金项目（51177115）；陕西省重点科技创新团队计划（2014KCT-16）；陕西省输变电设备状态监测工程技术研究中心项目（[2012]214）。

Project Supported by the National Natural Science Foundation of China（51177115）；Project of Key Science and Technology Innovation Team of Shaanxi（2014KCT-16）；Project of Shaanxi Research Center of Condition Monitoring of Power Transmission and Transformation Equipment（[2012]214）.

1674-3814（2017）03-0066-05

TM726

A