配网铁磁谐振过电压的非线性动力学分析及抑制措施的研究

朱岸明，王倩

（1.国网陕西省电力公司经济技术研究院，陕西西安 710065；2.西安理工大学自动化与信息工程学院，陕西西安 710048）

配网铁磁谐振过电压的非线性动力学分析及抑制措施的研究

朱岸明1，王倩2

（1.国网陕西省电力公司经济技术研究院，陕西西安 710065；2.西安理工大学自动化与信息工程学院，陕西西安 710048）

配电网中电磁式电压互感器引起的铁磁谐振过电压出现频繁，严重影响电力系统的稳定运行，研究一种快速、有效的消谐措施意义重大。利用非线性动力学对配电网系统发生的铁磁谐振过电压进行仿真分析，得到随着系统对地电容变化的分岔图及相应的最大李雅普诺夫指数曲线图，分析该系统下各类谐振的变化情况。在此基础上，研究配电网中性点经ZnO非线性电阻接地方式对铁磁谐振过电压的抑制方式，并获取能够抑制各类谐振的非线性电阻的伏安特性。结果表明：中性点经ZnO非线性电阻接地方式能够使过电压幅值降低到正常情况，同时混沌谐振现象消失，说明中性点经适当的非线性电阻可以有效地抑制铁磁谐振过电压。

铁磁谐振过电压；非线性动力学；分岔图；最大李雅普诺夫指数；ZnO非线性电阻；ATP-EMTP

城市配电网的发展与电缆的大量使用导致系统对地电容显著增大，使系统电感与对地电容的比值更加接近谐振条件范围，导致电磁式电压互感器（potential transformer，PT）饱和引起的铁磁谐振过电压现象频繁发生，影响电力系统的安全稳定运行。谐振过程产生持续稳定的过电流和过电压，往往会引起互感器等设备发生事故，造成人身伤亡。因此，研究铁磁谐振过电压现象并探索稳定可靠的消谐措施具有重要的现实意义和工程应用价值。

铁磁谐振是由铁芯的磁饱和效应引起铁芯电感非线性变化而产生的[1-4]，属于非线性系统领域，而混沌现象是非线性系统中普遍存在且较为复杂的一种现象。国内外研究现状表明，多数学者对铁磁谐振过电压的研究考虑到混沌振荡现象，但主要集中于改变激励的铁磁谐振变化情况，实际上忽略了系统接地电容对铁磁谐振的影响。

通过对国内外消除铁磁谐振过电压研究现状的分析可知，目前的消谐措施集中在PT、消弧线圈及小电阻接地方式[5-8]，针对中性点经非线性电阻消除铁磁谐振过电压的研究还很少。文献[9-12]对非线性电阻特性进行介绍，讨论将其添加在系统中性点作为新型接地方式的可行性，结合某10 kV配电网的实际情况，对不同接地方式进行分析探讨，得到适合该系统的接地方式。ZnO非线性电阻在正常情况下相当于是绝缘的，在电压达到一定的时候其阻值会变得很小，具有很好的可调控性，且能够消除谐振能量。

本文对系统中性点经ZnO非线性电阻接地方式抑制铁磁谐振现象进行了研究。首先对配电网不接地系统的谐振回路进行了分析研究，得到随着系统对地电容变化的分岔图及相应的最大李雅普诺夫指数曲线图，从而分析出该系统下各类谐振的变化情况。再获取中性点经ZnO非线性电阻接地系统的状态方程，通过仿真分析获取可以抑制各类谐振的最佳非线性电阻，进而分析该措施对铁磁谐振过电压的抑制效果。最后利用ATP-EMPT对这一抑制措施进行补充说明。

1 系统模型的建立

该10 kV不接地系统为110/10 kV的降压变电站，一台两绕组变压器，一次侧为星型接法，二次侧为△接法。图1为中性点不接地系统的接线简化图。图中PT为电磁式电压互感器，T为电力变压器，Rm为非线性电阻，L1、L2为系统的两条出线。

图1 系统接线简化图Fig.1 Equivalent circuit of a simple power system

PT的非线性电感饱和是导致铁磁谐振过电压的根本原因，深入研究非线性电感的伏安特性对充分认识铁磁谐振现象至关重要。本文利用JDZX9-10G型PT在工频下的高压侧试验数据进行分析，如表1所示，通过其电压-电流数据计算得到PT的磁通-电流，再经过“非线性最小二乘回归法”对磁通-电流数据进行拟合，得到PT的励磁特性曲线如图2所示，指数n表示励磁特性曲线通过拐点以后的弯曲程度。

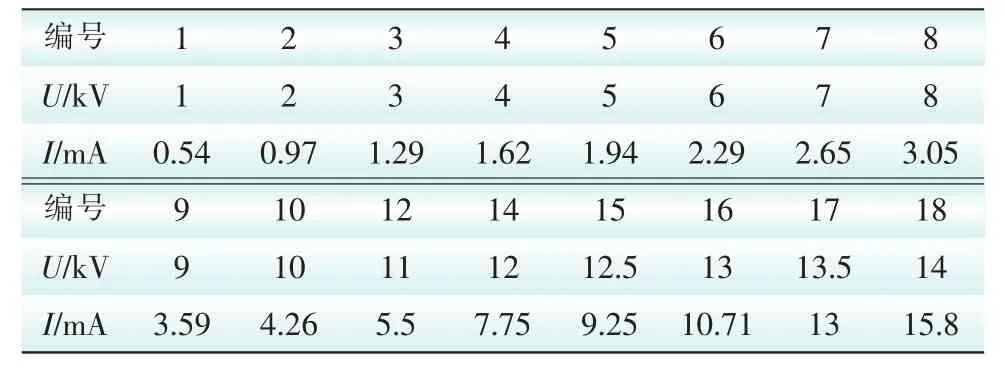
表1 工频下的高压侧试验数据Tab.1 The high voltage side test data in power frequency

图2 不同指数n拟合的励磁特性曲线Fig.2 The fitting magnetization curves with different n

拟合结果显示，当n=7或9时，拟合后的最优参数值不会发生变化，且拟合出的曲线接近原始数据。其他n值拟合的曲线差距比较大，如图2所示。通过参考文献[13]指出，当n=7时的电感伏安特性能够更好地反映其非线性特性，综合考虑得到非线性电感伏安特性多项式为

2 谐振系统的非线性动力学分析

运用非线性动力学理论分析该变电站由PT饱和引起的铁磁谐振现象。并应用以接地电容作为变量的分岔图与最大李雅普诺夫指数分析系统的状态随之变化的情况。

相轨迹表征了电压-磁通平面上每一点随时间的变化在平面上描绘出系统运动状态的演变过程。分岔图是指系统某参数发生变化，系统平衡点或周期轨道的模值，周期或似周期状态下为一个点或有限多个点，混沌状态下为无限多个点。

李雅普诺夫指数是衡量系统动力学特性的一个重要定量指标，表征了系统在相空间中相邻轨道间熟练或发散的平均指数率。2个系统若初始存在微小的差异，随着时间的变化产生分离，分离程度用李雅普诺夫指数来度量，为几何平均值的对数。

分岔图如图3所示，最大李雅普诺夫指数图如图4所示。

图3 分岔图Fig.3 Bifurcation diagram

图4 最大李雅普诺夫指数Fig.4 Maximum Lyapunov exponent

图3中，横坐标0～0.018 μF与0.023～0.037 μF这2个阶段数值所对应的点数为一个或有限多个，说明该阶段数值下的系统呈现周期或似周期状态。横坐标0.018～0.023 μF与0.037～0.050 μF这2个阶段数值所对应的点数繁多且无规律，说明此阶段数值下的系统呈现混沌状态。

图4中，横坐标0～0.018 μF与0.023～0.037 μF这2个阶段的最大李雅普诺夫指数小于零，表明此阶段系统处于稳定状态，与图5该阶段反映的系统呈周期与似周期状态相对应。横坐标0.018～0.023 μF与0.037～0.050 μF这2个阶段的最大李雅普诺夫指数大于零，表明此阶段系统处于混沌状态，与图5该阶段反映的系统呈混沌状态相对应。

由此确定，该变电站系统在接地电容为0～0.018 μF与0.023～0.037 μF时，系统发生周期谐振，在接地电容为0.018～0.023 μF与0.037～0.050 μF时，系统发生混沌谐振。

为了获得具体接地电容时系统的具体谐振情况，在混沌与周期阶段抽取以下几点，C=0.000 1 μF，C=0.010 μF，C=0.025 μF，C=0.040 μF，仿真得出系统在该电容下的电压、相轨迹以及频谱图如图5所示。

结合图3与图4分析得出的周期与混沌范围，在图5中可以根据电压、相轨迹以及频谱图分析得出系统在该接地电容下的具体谐振类别，结果分析如下所示。

1）如图5（a）所示，当C=0.001 μF时，系统处于非混沌状态，由电压图看出系统电压并未升高，处于正常电压范围，为正弦函数，相轨迹图呈现一个周期轨道，此时系统是稳定的，频谱图显示系统处于50 Hz，更加验证系统处于稳定状态，且正常情况；

2）如图5（b）所示，当C=0.010 μF时，系统处于非混沌状态，接下来再由电压图看出系统电压升高至1.5pu，波形虽然不是为正弦函数但依然呈现一定的周期性，相轨迹图呈现一个近似周期轨道，此时系统是稳定的，频谱图显示系统处于1/3工频，说明系统处于稳定状态要，且发生了分频谐振；

3）如图5（c）所示，当C=0.025 μF时，系统处于非混沌状态，接下来再由电压图看出系统电压升高至3.2pu，波形虽呈现一定的非周期性，相轨迹图出现似周期轨道，此时系统是稳定的，频谱图显示系统处于1/3工频，1/2工频及工频，但是分频所占分量较大，说明系统处于稳定且发生了分频谐振；

4）如图5（d）所示，当C=0.040 μF时，分岔图表现混乱无章，最大李雅谱诺夫指数为正值，表明系统处于混沌状态，接下来再由电压图看出系统电压升高至3.9 pu，波形虽呈现一定的非周期性，相轨迹图出现奇怪吸引子，此时系统是不稳定的，频谱图显示系统在各个频率段都有，说明系统处于不稳定状态，即混沌状态。

图5 系统在不同电容值下的状态响应Fig.5 State response of system in different capacitor

3 非线性电阻对系统谐振的影响

ZnO非线性电阻具有良好的非线性特性，在系统正常情况下非线性电阻相当于绝缘，系统仍处于不接地方式，在系统电压达到一定值时，ZnO非线性电阻内部则导通，呈小电阻状态，此时系统近似于小电阻接地方式，具有很好的可调控性，因此能够很好地消除谐振能量。

3.1 添加非线性电阻后系统数值模型的建立

图6中C表示系统的对地电容；R表示系统的内电阻；RP表示PT的直流电阻；L表示PT的非线性电感。模型中没有考虑二次侧和开口三角侧漏抗的影响，因此用电阻和非线性电感的并联等效代替PT[13]。

对图6所示的等效电路进行数学分析，根据KCL、KVL可以得到系统状态方程如下所示：

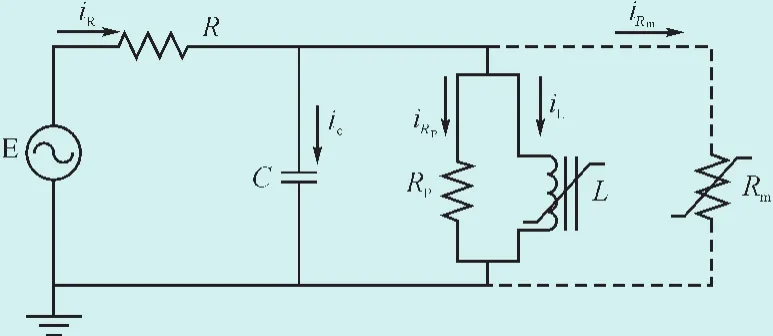
图6 系统谐振等效电路Fig.6 Ferroresonance simplified equivalent circuit

由式（2）化简得到系统的状态方程如下：

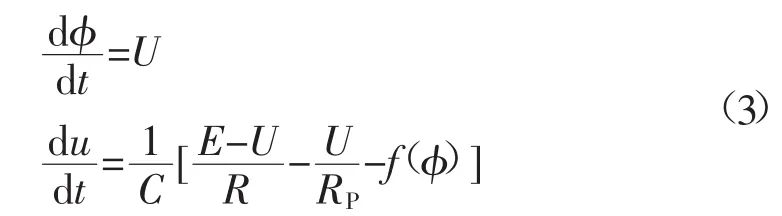
为了简化式（3）的状态方程，将系统谐振电路进行归一化处理，

3.2 非线性电阻最佳伏安特性曲线的获取

中性点经非线性电阻接地方式对铁磁谐振过电压的抑制作用取决于非线性电阻伏安特性的非线性指数，所以获取合适的非线性电阻表达式也相当重要。其伏安特性通常描述为[15-16]

式中，α表示与电阻材料和结构尺寸有关的常数，可用来表示非线性电阻阀片的非线性特性，称作非线性指数，其β值愈大，说明非线性电阻阀片的非线性越强。

中性点不接地系统中将非线性电阻接入到由接地变压器引出的中性点上，所添加非线性电阻采用10 kV氧化锌非线性电阻片，根据其伏安特性曲线拟合得到公式（5）中的参数为

一般非线性电阻对系统谐振现象的抑制效果不明确，则需要通过大量仿真得到可以消除铁磁谐振过电压的最佳伏安特性曲线。因此本文研究了非线性特性曲线的非线性系数发生变化时，系统响应状态随之发生变化的过程，结果如表2所示。

表2 不同值的系统响应状态Tab.2 System response in different β value

由表2可以得到，当β值为7.9和8.1时分频电压接近为正弦；β值为8.5时，基频和分频电压波形图只是部分正弦波；β值为8.9时，高频部分电压波形图只是部分正弦波；β值为9.1时高频部分没有消谐效果，分频与高频电压波形图只是部分正弦波。

当β在6.1～7.9范围之内时，对不同类别的铁磁谐振过电压都有一定的抑制效果，但其过电压的幅值在1.8～0.73倍以内，周期性较理想，而电压波形振荡较严重。当β=8时，各类谐振过电压倍数抑制在相电压左右，且电压波形图近似正弦波，且周期性较好，所以伏安特性曲线的最佳非线性指数为8。

从而得到最佳非线性曲线的表达式为

3.3 系统仿真分析

当非线性电阻伏安特性发生变化时，系统的响应状态从混沌变为似周期再变为周期，同时过电压倍数逐渐降低。将式（6）代入到式（4）进行仿真分析，结果如图7所示。

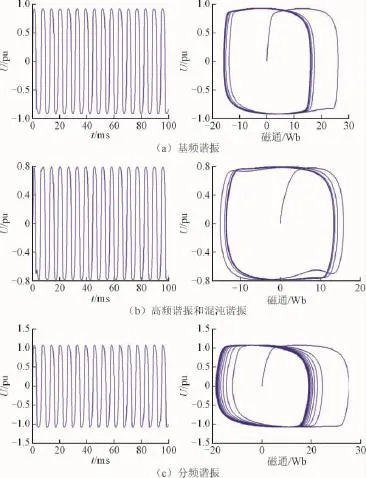
图7 中性点接ZnO非线性电阻接地系统各类谐振情况下PT的电压波形及相轨迹图谐振情况Fig.7 Voltage waveform and space trajectory of PT under various ferroresonances when the system neutral point is through ZnO nonlinear resistance

仿真结果如图8所示，对于基频、高频谐振，其消谐效果比较明显，电压恢复到相电压，相轨迹图呈周期性，但对于分频谐振，其仍存在振荡情况，较基频谐振情况相比，消谐效果较差。混沌现象消失，过电压降低至接近相电压。

将图7与图5中不同类别谐振情况下的电压波形图与相轨迹图进行对比分析，结果表明，对于不同谐振类型，所添加的非线性电阻伏安特性会有区别。系统中性点接入非线性电阻后，不同类型的谐振过电压倍数都降低至相电压左右，其相轨迹图由混沌状态转变为“似周期”或“周期”状态，说明非线性电阻对铁磁谐振过电压具有良好的消谐作用，针对不同类别谐振，同一伏安特性的非线性电阻对其的消谐作用不尽相同，当改变非线性电阻的非线性指数时，即针对不同类型谐振，当添加不同伏安特性的非线性电阻其会产生相同的消谐效果。

图8 投入非线性电阻之后的仿真结果Fig.8 Simulation result with the system neutral point being through nonlinear resistance

3.4 ATP仿真验证

根据图1所示的某实际变电站的系统接线简化图在ATP-EMTP中搭建模型。在搭建模型时，设置系统A相在0.06 s发生单相接地故障，0.08 s消失，而运行0.2 s时系统的中性点接入ZnO非线性电阻，最终的仿真结果如图8所示。

系统在单相接地故障消除后，导致PT饱和产生铁磁谐振过电压。图8（a）、8（b）分别表示系统故障相和非故障相的谐振电压波形。系统发生谐振后在0.2 s接入非线性电阻。图8（c）、8（d）分别表示系统故障相和非故障相的稳定电压波形。

当在投入非线性电阻后，其消耗了谐振能量，致使0.22 s后铁磁谐振消失，系统在短时间内达到稳定并恢复至正常电压。说明在本系统添加的非线性电阻起到了很好的抑制作用。

4 结论

本文利用非线性动力学分析系统中性点经ZnO非线性电阻接地方式抑制铁磁谐振过电压，得到以下主要结论。

1）系统中性点经ZnO非线性电阻接地的抑制措施，无论是混沌谐振还是周期谐振，其产生的消谐效果较为明显，过电压恢复至8.8 pu左右，相轨迹图呈周期性结果，使系统趋于稳定状态。

2）以接地电容的参数为变量，作出谐振系统的分岔图与最大李雅普诺夫指数图。分析得到系统在不同接地电容下属于周期谐振或是混沌谐振。

3）获得了可以同时抑制不同类别谐振的最佳ZnO非线性电阻伏安特性曲线。通过在ATP建立某实际变电站模型对这一措施进行仿真验证，结果表明系统中性点接入非线性电阻之后，PT电压幅值降到正常情况下，且混沌现象也消除了。

[1]徐正宏，吴奇.电力系统铁磁谐振消谐方法研究[J].电力学报，2014，29（6）：532-537.XU Zhenghong，WU Qi.Study on the harmonic elimination of power system ferromagnetic resonance[J].Electric Power Journal，2014，29（6）：532-537.

[2]周默，孙岩洲.电网中性点不同接地方式下铁磁谐振的消谐研究[J].高压电器，2015，51（1）：80-85.ZHOU Mo，SUN Yanzhou.Study on the harmonic elimination of ferromagnetic resonance in different grounding modes of power network[J].High Voltage Apparatus.2015，51（1）：80-85.

[3]曾祥君，杨先贵，王文，等.基于零序电压柔性控制的配电网铁磁谐振抑制方法 [J].中国电机工程学报，2015，35（7）：1666-1673.ZENG Xiangjun，YANG Xiangui，WANG Wen，et al.Based on the flexible control of zero sequence voltage distribution network ferroresonance suppression method [J].Proceedings of the CSEE，2015，35（7）：1666-1673.

[4]李凤舞，姜涛.单相接地引起电压互感器烧毁事故原因分析[J].自动化应用，2013（12）：84-85.LI Fengwu，JIANG Tao.Cause analysis of burnout accident of voltage transformer caused by single-phase grounding[J].Automation Applications.2013（12）：84-85.

[5]周浩，余宇红，张利庭，等.10 kV配电网铁磁谐振消谐措施的仿真比较研究[J].电网技术，2005，29（22）：24-34.ZHOU Hao，YU Yuhong，ZHANG Liting.et al.Comparative study on ferroresonance elimination measures in 10 kV distribution system by simulation method[J].Power System Technology，2005，29（22）：24-34.

[6]翁利民，陈灵欣，靳剑峰.配电网电压互感器铁磁谐振的特点与抑制[J].继电器，2004，32（20）：40-42.WENGLimin，CHENLingxin，JINJianfeng.Thecharacteristicsoftheferromagneticresonancevoltagetransformer and inhibit the distribution network[J].Relay，2004，32（20）：40-42.

[7]王鹏，郭洁，齐兴顺，等.35kV中性点经消弧线圈接地系统几种铁磁谐振消谐措施有效性分析[J].电磁避雷器，2010（6）：34-37.WANG Peng，GUO Jie，QI Xingshun.The effctiveness analysis of ferroresonance suppression measures for 35 kV neutral point through arc suppression coil grounded system [J].Insulators and Surge Arresters，2010（6）：34-37.

[8]童奕宾，尤智文，李姝.小电阻接地系统间歇性弧光过电压分析 [J].电力系统及其自动化学报，2012，24（3）：116-120.TONG Yibin，YOU Zhiwen，LI Shu.Small grounding system of intermittent arc over-voltage analysis[J].Electric Power System and its Automation.2012，24（3）：116-120.

[9]EDA K.Destruction mechanism of ZnO varistors due to high current[J].Journal of Applied Physics，1984，56（10）：2948-2955.

[10]陈先禄，田凤兰，许文强，等.非线性电阻限制10kV电网弧光接地过电压分析[J].重庆大学学报（自然科学版），2006，29（7）：38-40.CHEN Xianlu，TIAN Fenglan，XU Wenqiang.Nonlinear limit analysis of 10 kV power grid over-voltage of arc light earthing Journal of Chongqing University（Natural Science Edition），2006，29（7）：38-40.

[11]兰宇.城区10kV配电网中性点接地方式的探讨[J].上海电力，2010（2）：151-154.LAN Yu.City 10 kV distribution network neutral point grounding way[J].Shanghai Electric Power.2010（2）：151-154.

[12]李春晖，梁学东，潘蕾蕾.10 kV配电网中性点经非线性电阻接地方式探讨[J].山西电力，2007（5）：52-54.LIChunhui，LIANG Xuedong，PAN Leilei.10kV distribution network neutral point grounding way by the nonlinear are discussed[J].ShanxiElectric Power，2007（5）：52-54.

[13]XIA P.Analysis of ferromagnetic chaotic circuit with nonlinear potential transformer[J].Acta Physica Sinica，2013，62（15）：150504.

[14]杨庆，郑哲人，司马文霞，等.避雷器对具有混沌效应铁磁谐振过电压的影响 [J].高电压技术，2011，37（1）：40-49.YANG Qing，ZHENG Zheren，SIMA Wenxia，et al.Effects of MOA on chaotic ferroresonance overvoltage[J].High Voltage Engineering.2011，37（1）：40-49.

[15]庞霞，刘崇新.含电磁式电压互感器的铁磁混沌电路的分析研究[J].物理学报，2013，15：60-65.PANG Xia，LIU Chongxin.Including electromagnetic voltage transformer of ferromagnetic chaotic circuit analysis [J].Journal of Physics.2013，62（15）：60-65.

[16]代姚，司马文霞，孙才新，等.运用T-S模糊方法对铁磁谐振过电压的混沌抑制[J].高电压技术，2010， 36（4）：878-883.DAI Yao，SIMA wenxia，SUN Caixin，et.al.Chaos controlling in ferroresonance overvoltage with T-S fuzzy method[J].HighVoltageEngineering，2010，36（4）：878-883.

Nonlinear Dynamic Analysis and Suppression Method of Ferroresonance Overvoltage in Distribution Network

ZHU Anming1，WANG Qian2
（1.Economic Research Institute of State Grid Shaanxi Electric Power Company，Xi’an 710065，Shaanxi，China；2.School of Automation and Information Engineering，Xi’an University of Technology，Xi’an 710048，Shaanxi，China）

Ferroresonance overvoltage caused by the potential transformer occurs frequently in distribution networks, which affects the stable operation of the power system seriously.Therefore,a reliable,stable and convenient way to eliminate the ferroresonance is urgently in need.In this paper,the magnetization curve of the potential transformer is obtained by calculating the test dates of JDZX9-10G,and different types of ferroresonance are analyzed by the space trajectory.On this basis,the ferroresonanceovervoltageinhibiting with ZnO nonlinear resistance grounding mode is researched,and the acquisition of ZnO nonlinear resistance is described in detail.The method is verified by ATP-EMTP and the results show that the voltage amplitude of the neutral point through nonlinear resistance decreases to normal circumstances and the chaotic phenomena is eliminated,which means that the resonance elimination measure of neutral point through nonlinear resistance can well inhibit the ferroresonance overvoltage.

ferroresonance overvoltage；noninear dynamic；the magnetization curve；the space trajectory；ZnO nonlinear resistance；ATP-EMTP

2016-12-06。

朱岸明（1973—），男，硕士，高级工程师，从事电力系统分析规划、电网运行分析方面的工作。

（编辑 冯露）

国家自然科学基金（51507135）。

Project Supported by the National Natural Science Foundation of China（No.51507135）.

1674-3814（2017）03-0028-07

TM864

B

王 倩（1982—），女，博士，副教授，硕士生导师，研究方向为电力系统电磁暂态计算、电力系统电介质材料特性分析。