基于有限元分析的五相感应电机参数计算

郝晓辉，李 耕



基于有限元分析的五相感应电机参数计算

郝晓辉1，李 耕2

（1. 海装天津局，天津 300074；2. 海军工程大学，武汉430033）

以自行设计的一台五相感应电机为例，分析了多相感应电动机内部的电磁关系，建立了多相感应电机二维静、瞬态电磁场考虑边界条件的偏微分方程，并在此基础上，对五相感应电动机的暂、稳态电磁场和电机性能进行计算；分别应用场算和路算方法计算了励磁电感，并与设计值进行对比，结果表明本文所用的电磁场计算方法准确有效。

五相感应电机 参数计算 有限元 励磁电感

0 引言

感应电机具有结构简单、运行可靠、维修方便等优点，且大功率电力电子技术的日益成熟又弥补了其在起动、调速性能等方面的不足，随着舰船综合电力技术的发展，大容量感应电机已成为舰船电力推进的首选电机[1-2]，也使得多相感应电机的重要地位日益凸显出来。而多相电机发展的最初目的是为了解决三相电机输出转矩低频脉动的问题，因为转矩脉动的频率随着电机相数的增加而升高[3]；其次是为了提高系统的可靠性，并且随着电机相数的增加，相电流会大大减小[4]。上世纪九十年代中期，船舶电力推进技术加速了多相电机及其驱动系统的发展，这也是目前多相电机系统的主要应用之一[5-8]。与三相电机相比，多相电机的优势可归纳如下[9-10]：

1）在不增加相电压的前提下，每相电流减小，降低了对功率器件容量的要求。

2）随着电机相数的增加，输出转矩脉动的频率提高且幅值大大减小，显著改善了电机运行性能，特别是低速时的运行性能。

3）多相电机具有更多的控制自由度，这使得多相电机的控制系统更为灵活，便于提高控制系统的性能。

4）多相电机系统的可靠性高，即使其中的一相或几相出现故障，通过适当的控制仍可以保证电机的正常起动和运行。这对提高舰艇生命力有十分重要的意义。

多相电机的诸多优点使其拥有广阔的应用前景，但随着其相数增多，需计算的变量也急剧增加，给多相电机的设计和分析带来了很大困难。电机参数是研究电机运行性能的关键参量，而且对变频器供电调速系统的性能分析和仿真也极为重要，因为整个系统的模型都需要这些参数来确定。而如果在电机设计阶段就能够准确计算出这些参数，那么就可以方便地进行设计方案的调整，也更易于电机参数的合理匹配，从而缩短研发周期和降低成本。

本文以自行设计的五相感应电机为例，详细讨论了其主要电感参数的计算方法，结合实例进行计算，并给出场算、路算与设计值的对比结果。

1 电机仿真模型的建立

建立五相异步电机的二维有限元模型，见图1。建模过程如下：

1) 选择求解平面—XY平面；

2) 确定电机结构尺寸、画出模型；

3) 确定电机材料属性；

4) 确定有限元计算的边界条件和外加源参数；

5) 确定计算过程中是否考虑各种损耗；

6) 确定动态参量，包括：运动边界，外加载荷、时间步长等。

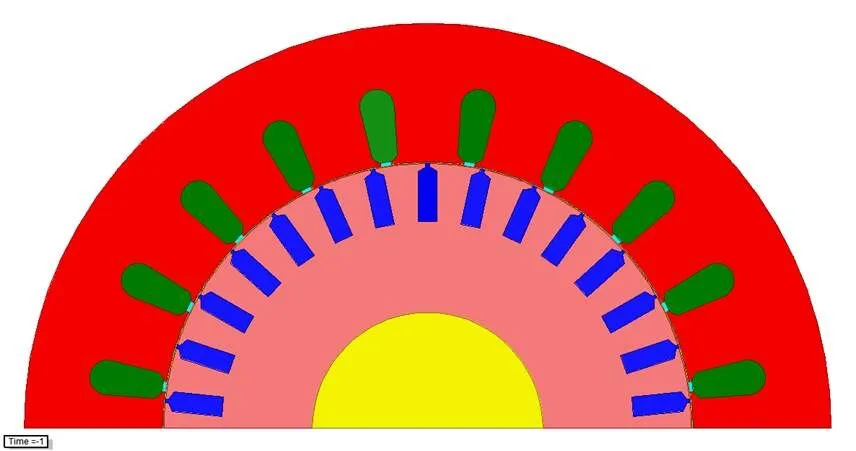
图1 电机仿真模型

电机的结构参数见表1。

表1 电机模型参数列表

电机额定功率为5.5 kW，定子Y连接方式，相电压150 V，频率50 Hz。由于建立的是二维模型，故不考虑端部及转子斜槽的影响。定转子铁心采用0.35 mm硅钢片。定子为短距分布式双层绕组，导线材料为铜。转子采用鼠笼形式，导条为铸铝。电机的绝缘等级为F，故在进行材料属性的设定时，定转子的电阻率都设为F级绝缘平均工作温度115°C时的电阻率。

2 仿真的数学模型

有限元仿真的求解区域为整个模型区域。由于模型中有定子绕组，绕组中有电流流过，所以，对于该模型中的电磁场问题，应采用矢量磁位A作为求解变量。

麦克斯韦方程组的微分形式为：

在应用电磁场理论进行分析时需注意，所研究的电机属于似稳电磁场。对于似稳电磁场，麦克斯韦方程组中(1)式中位移电流密度与传导电流密度相比可以忽略不计。即在研究似稳电磁场问题时，只考虑磁场变化所产生的电场，不考虑电场变化所产生的磁场。

在所建立的二维瞬态场分析时，将上述方程组改写为时变方程组的以下形式[4]：

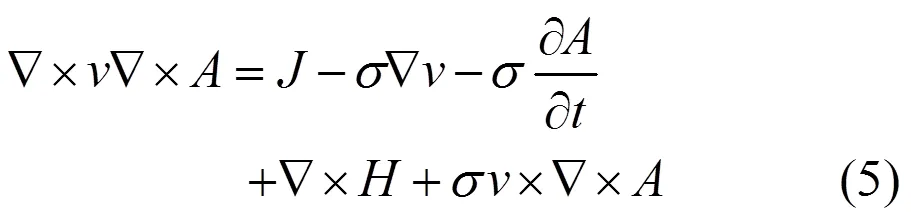
其中：是运动速度；是磁矢量；是电流密度。

3 仿真分析及参数计算

铁磁材料的非线性对电感的计算结果影响重大，本文将分别用经典路算(不考虑铁磁材料非线性)和场算(考虑非线性)的的方法对励磁电感进行计算，并与设计值进行比较。使用有限元分析软件Ansoft Maxwell 2D，为更接近真实工况，采用瞬态场进行计算。

由励磁电感的定义，当多相绕组中通以多相对称电流后，由电枢电流所建立的气隙磁场所对应的电感即为励磁电感。与静态场不同，Maxwell 2D瞬态场可以对电机的暂、稳态进行分析。考虑到转子导条和转差对气隙磁场的影响，本文将采用瞬态场计算励磁电感。

为节省计算资源，加快仿真速度，建模时采用二分之一模型。由于瞬态场中软件无法自动计算定子绕组的电阻，故电阻需要单独设置。为增加仿真的准确性，本文采用电桥法对定子绕组相电阻进行测量，经多次测量结果取平均值，得相电阻s=1.32 Ω。

定子端加入五相对称正弦电压，为进一步逼近工况，所加电压幅值为212 V，频率为50 Hz，转子从零速起动，直至稳态。转子初始速度设为零。

定转子铁心材料的非线性对仿真结果颇有影响，故仿真时所用硅钢片与实际电机相一致，其磁化曲线如图2所示：

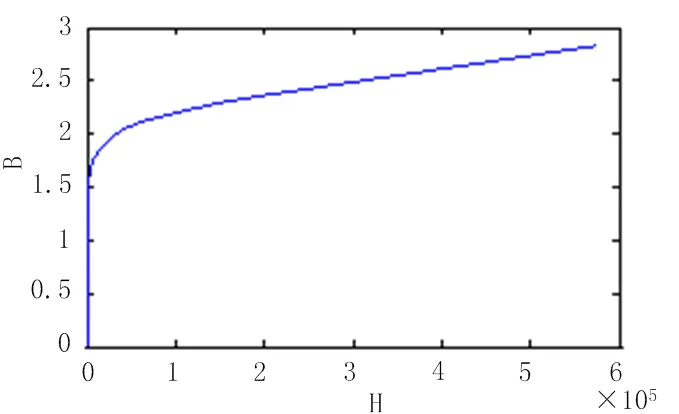
图2 DW540 B-H曲线

其他参数设置这里暂不赘述。

所加端电压周期为0.02 s，令软件在一个电周期内计算100次，将仿真步长设为0.00002 s，所得稳态结果如下图。

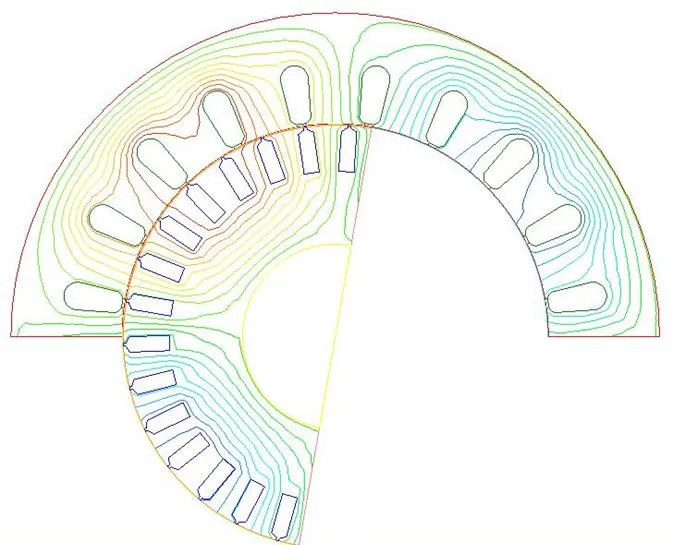
图3 稳态时电机磁场分布图

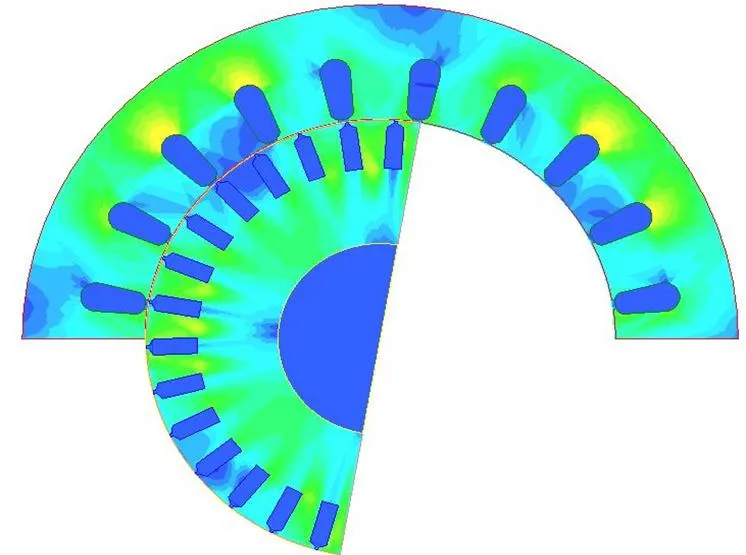
图4 稳态时磁密分布云图

图5 网格剖分图

图6 稳定运行时转子位置角与时间关系图

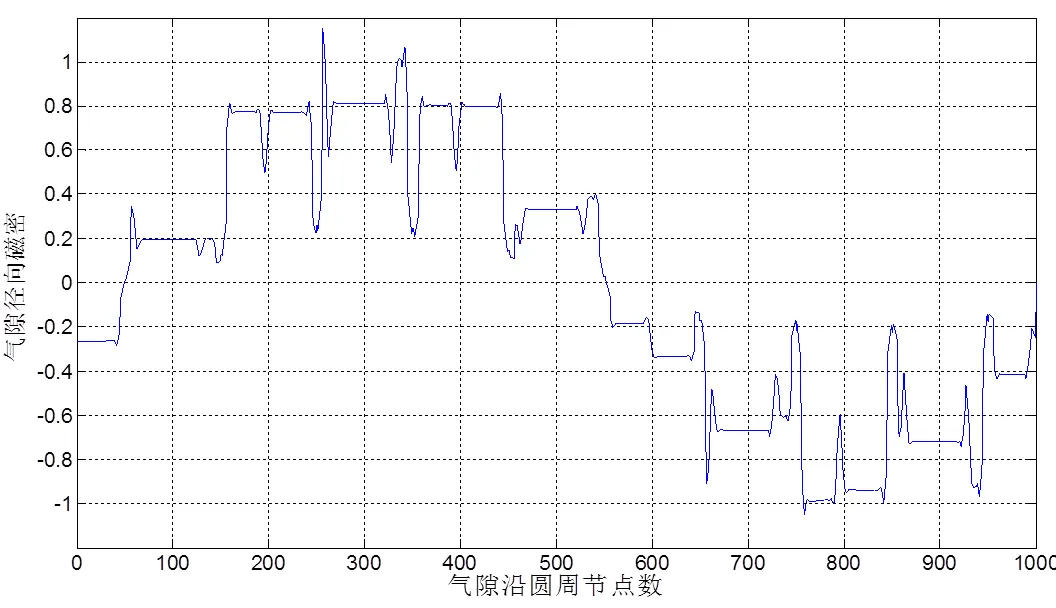
图7 空载时气隙径向磁密分布（铁磁材料非线性）

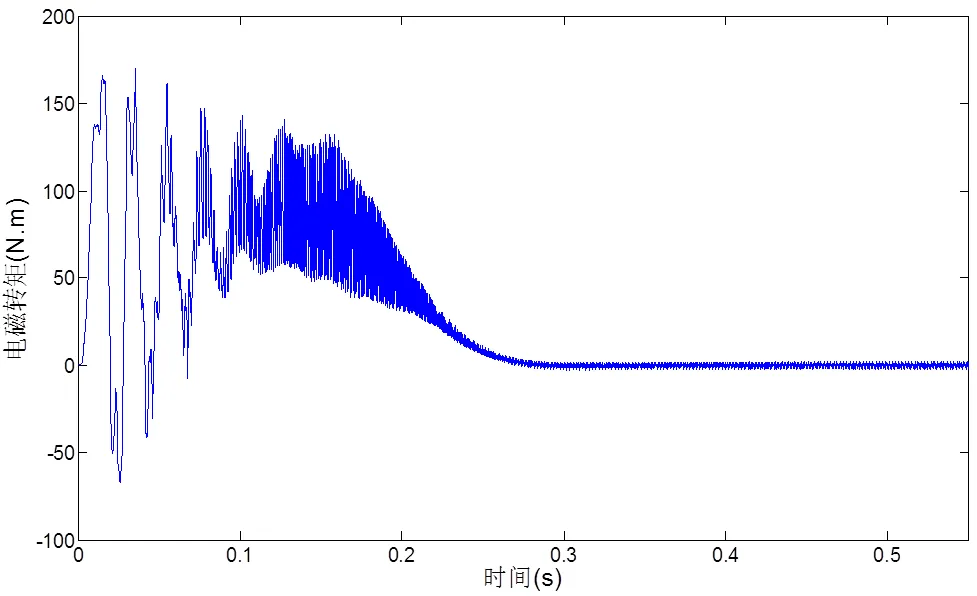
图8 稳定运行时转矩与时间关系图

由图6~图9可知，电机稳态时运转正常，仿真参数设置正确。

稳定后，在后处理器中，通过场计算器将气隙磁密的径向分量提取出来。由于齿槽和高次谐波磁势的存在，使得径向磁密并非标准正弦波，但上述公式中所用各量均为基波分量，为此，作者编制了MATLAB程序，将磁密中的基波和各次谐波提取出来，如图10所示。

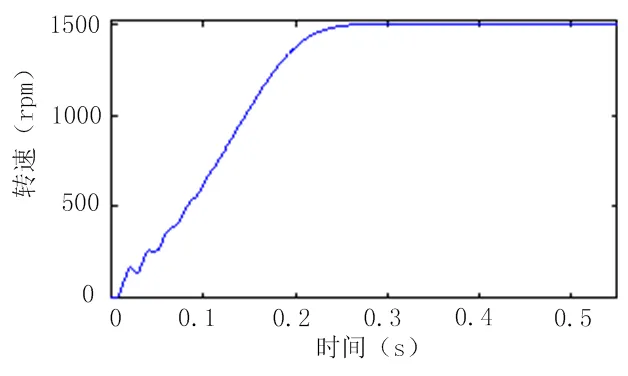
图9 稳定运行时转速与时间关系图

图10 空载时气隙径向磁密及其基波(铁磁材料非线性)

上图中，气隙磁密的基波幅值为0.812 T。

用同样的方法，将稳态时A相电流及其基波提取出来，如图11所示。

图11中，基波电流幅值6.5676 A。应用以上算得的和的结果，得到励磁电感为

m1=0.09 H

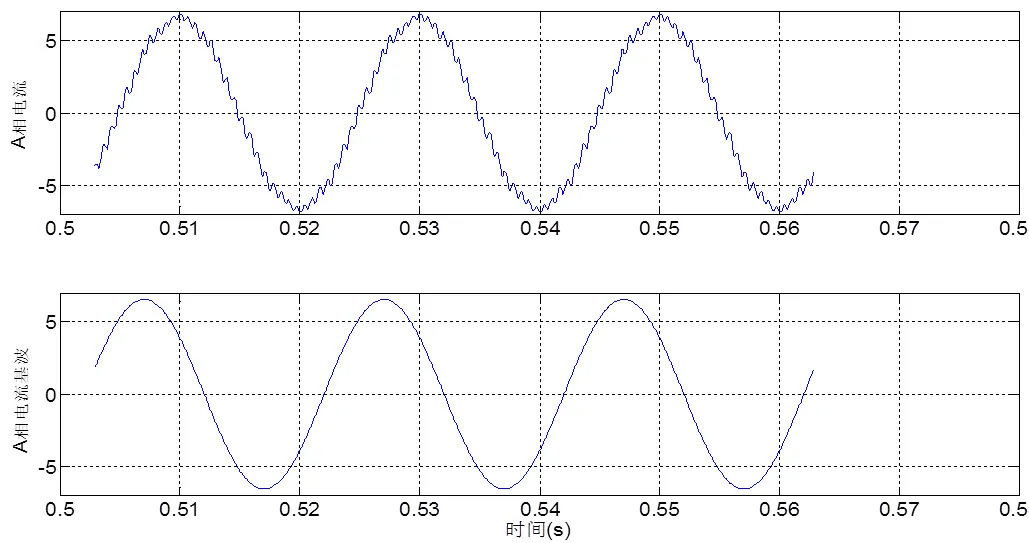
图11 稳态时A相电流及其基波(铁磁材料非线性)

由于

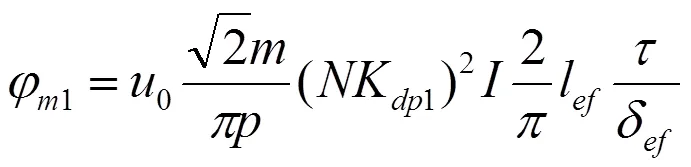
于是

(7)

应用上述公式，算得励磁电感为：

m1=0.17 H

为进一步说明问题，现用有限元计算软件来模拟上述计算过程。

在Maxwell 2D瞬态场中，将定转子铁心所用硅钢片的磁导率设为1000 H/m，即励磁电流与磁链呈线性关系，如图12所示。其中，基波幅值为0.819T。用同样的方法将定子绕组A相电流及其基波分量提取出来，如图13所示。其中，基波电流幅值3.9724 A。

这样，得到B和I的基波幅值之后，得到励磁电感为

m1=0.169 H

可见，上述两种方法算得的结果基本一致。

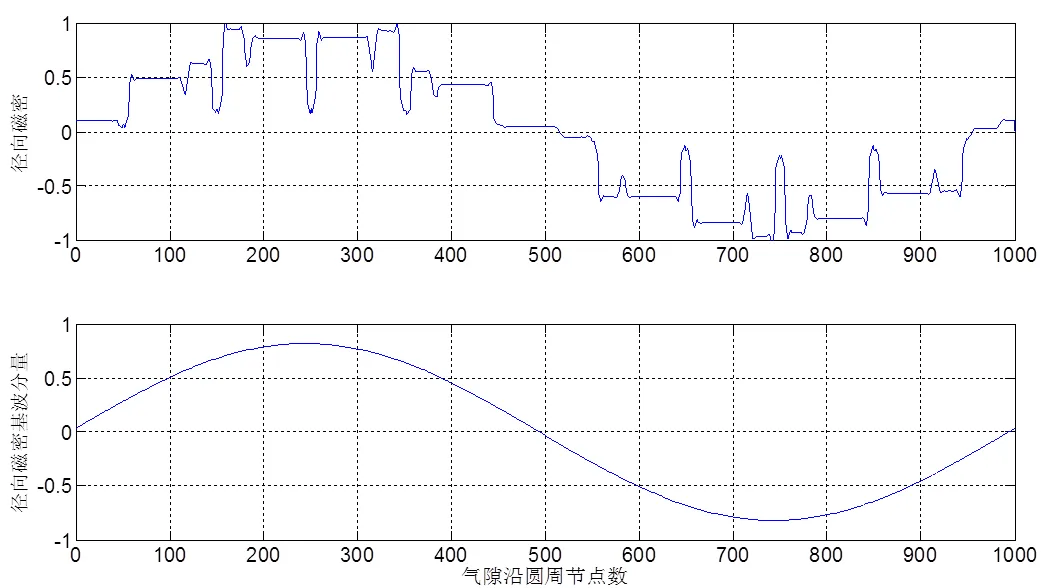
图12 空载时气隙径向磁密及其基波(线性铁磁材料)

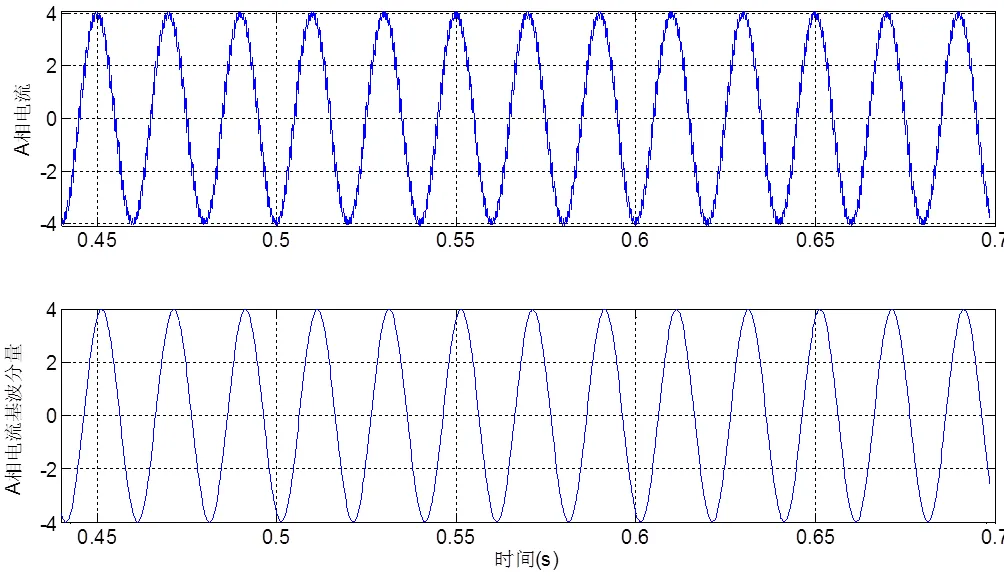
图13 稳态时A相电流及其基波(线性铁磁材料)

励磁电感的计算值和设计值的比较如表2所示。

表2 励磁电感计算值与设计值比较

由以上计算和比较结果可知，铁磁材料对感应电机励磁电流影响较大，在计算励磁电感时，不计入铁磁材料非线性将会产生较大误差。

4 结论

本文以自行设计的一台五相感应电机为例，分析了多相感应电动机内部的电磁关系，并分别用场算和路算方法计算了一台5.5 kW五相感应电机的励磁电感，计算结果表明，与设计值相比，路算误差为7%，而场算误差仅为0.9%，场算结果更准确，并对计算结果进行分析，找到路算方法误差较大的原因。

[1] Clayton D H, Sudhoff S D, Grater G F. Electric ship drive and power system[C]. International Power Modulator Symposium, Norfolk, Virginia, USA, 2000.

[2] Smith A C, Williamson S, Hodge C G. High torque density naval propulsion motors[C]. IEEE International Conference on Electric Machines and Drives, Wisconsin, USA, 2003.

[3] Ward E E, Härer H. Preliminary investigation of an invertor-fed 5-phase induction motor[J]. Proc. Inst. Electr. Eng., 1969, 116(6): 980-984.

[4] Levi E. Multiphase electric machines for variable-speed applications[J]. IEEE Transactions on Industrial Electronics, 2008, 55(5): 1893-1909.

[5] McCoy T, Bentamane M. The all electric warship: An overview of the U.S. Navy’s integrated power system development programme[C]. Proc. Int. Conf. Elecship, Istanbul, Turkey, 1998: 1-4.

[6] Benatmane M, McCoy T. Development of a 19 MW PWM converter for U.S. Navy surface ships[C]. Proc. Int. Conf. Elecship, Istanbul, Turkey, 1998: 109-113.

[7] Terrien F, Siala S, Noy P. Multiphase induction motor sensorless control for electric ship propulsion[C]. Proc. IEE PEMD Conf., Edinburgh, U.K., 2004: 556-561.

[8] Ferreira C L, Bucknall R W G. Modelling and real-time simulation of an advanced marine full-electrical propulsion system[C]. Proc. IEE PEMD Conf., Edinburgh, U.K., 2004: 574-579.

[9] 庄朝晖, 熊有伦, 马挺. 多相感应电机变频调速系统－回顾、现状及展望[J]. 电气传动, 2001(2): 3-7.

[10] 陈林, 熊有伦. 多相感应电动机调速系统研究与应用[J]. 微特电机, 2002(1): 33-38.

Parameter Calculation of Five-phase Induction Motor Based on FEA Method

Hao Xiaohui1, Li Geng2

( 1. Tianjin Bureau of Naval Equipment Department, Tianjin 300074, China; 2.Naval University of Engineering, Wuhan 430033, China)

TM461

A

1003-4862（2017）04-0050-05

2016-10-20

郝晓辉（1984-），男，助理工程师。研究方向：船舶电力推进。E-mail:653462459@qq.com

李耕（1990-），男，博士研究生。研究方向：电力系统、电力电子与电力传动。