整治工程对概化分汊河口分流和分沙影响分析

吴明珠，潘 昀

(1.湖南省航务勘察设计研究院, 湖南 长沙 410005; 2.浙江海洋大学 国家海洋设施养殖工程技术研究中心， 浙江 舟山 316000)

整治工程对概化分汊河口分流和分沙影响分析

吴明珠1，潘 昀2

(1.湖南省航务勘察设计研究院, 湖南 长沙 410005; 2.浙江海洋大学 国家海洋设施养殖工程技术研究中心， 浙江 舟山 316000)

河口是连接河流和海洋的纽带，也是海上运输的启程点和目的地。河口航道的自然水深难以满足航运的需求，因此需要对航道进行整治和疏浚，但整治工程对分汊河口的影响机制并不明确。以明渠均匀流为验证基础，建立分汊河口不同整治工程概化水沙数学模型，探讨均匀流和正规半日潮作用下一汊开挖航道和建设丁坝群后对另一汊河道的水沙动力影响。研究结果表明，断面泥沙通量与断面流量变化不一致，存在最优丁坝长度，通过回归性分析得到优良相对长度0.62和极限长度0.78使得断面流量和泥沙通量受丁坝影响较小。此计算模式仅能得出航道的开挖对分汊河道的分流和分沙有较大的影响。均匀流和潮流作用下周期内断面的分流比存在一致性，分沙比在0.5左右时各工况潮流影响略有不同，潮流对汇流处分沙比的影响值得进一步的深入研究。研究结果为减少航道维护和整治分汊河口提供参考，也为分汊河口物理模型试验提供理论依据。

航道； 整治工程； 分汊河口； 水沙动力

0 前言

分汊河口的江心洲往往空间尺度比较大，由于护岸工程的存在也较稳定，所以与分汊河道在空间上有许多不同。径流和潮流共同作用的动力条件也较为复杂，并且河口均存在一定的放宽率。航道整治工程在影响局部水沙运动的同时长时间作用后可能会对整体系统带来影响，而这部分影响往往却被忽略。

我国对航道整治工程影响下的河道水沙运动研究较多，研究深入数值计算，水槽试验和相似物理模型试验。谈广鸣[1,2]对分汊河道冲淤和悬移质分沙进行了系统的研究，得出单个丁坝对水沙运动的影响机制和悬移质的分布情况。近3年对于长江口水沙动力问题逐渐开展，窦润青[3]将长江口南槽和北槽作为一个整体系统，利用实测地形资料和FVCOM数值模型计算流场，研究近10余年北槽落潮分流比和分沙比的变化原因。童朝峰[4]利用分汊水槽进行分汊口水流结构和底沙输沙试验，研究不同支汊流量、不同泥沙粒径及分汊角度对分流分沙比的影响和分汊口泥沙输沙机理。Amaurthy等[5,6]通过分汊水槽试验，验证其由动量方程得出的分流比、两分汊Fr数和水深的关系。Barkdoll等[7]对直角分汊口的底沙运动做了初步测试。Neary等[8]人实验测定了直角分汊口的水流结构，得到一些分流面的变化规律。

从国内外对分汊河口水沙运动研究来看，动力从均匀流到潮流逐渐由简单到复杂对分汊河口进行认识。以往的研究多抓住航道整治工程内部，比如丁坝附近水流结构和悬疑质分布或者航道滩槽环流结构和泥沙运动等细节，对内在机制进行深入研究，为数学模型和物理模型寻求可靠的理论依据。近年来许多河口因一汊整治工程的存在对另一汊带来许多不利影响，并且这方面的理论基础多属空白。于是非常有必要把分汊河口的两汊作为一个整体系统进行研究，探讨整治工程一汊与另一汊的一般性相互作用机制。因此本文首先详细阐述全沙均匀流数学模型，并以此为基础率定各种参数，然后建立分汊河口不同整治工程概化水沙数学模型，探讨均匀流和正规半日潮作用下一汊开挖航道和建设丁坝群后对另一汊河道的水沙动力影响。为对分汊河口水沙运动的进一步研究提供参考。

1 计算方法

建立非结构网格概化模型，解析水动力方程和全沙非平衡输沙方程探讨均匀流和正规半日潮作用下一汊开挖航道和建设丁坝群后对另一汊河道的影响以及分汊河口因航道整治引起的水沙动力响应。

1.1 网格建立

Delaunay三角剖分算法是构建数字高程模型(DEM)的主要算法，具有快速、高效的内存交换特点，可以稳定的计算用户指定的孔和凹槽等特殊的三角形区域。三角形算法在网站上免费提供源代码，提供许多包括三角剖分的算法和数据结构实施方法，以及建立和完善网格的步骤，解决算法中出现稳定性问题。

1.2 解析方法

模型基于非结构网格和非压缩雷诺方法调用Boussinesq假设和静水压力解析平均的斯托克斯方程实现。因此模型涉及连续方程，动量方程和密度方程，通过平均紊流方程进行闭合求解。方程组的空间离散采用中心有限体积法进行。浅水方程和运动方程的时间积分有两种方法低阶和高阶，低阶的方法是一阶显式欧拉方法，高阶的方法是二阶Runge-Kutta方法。

沿闭边界(陆地边界)的所有变量的强迫控制为零。开边界可以指定定量的流量和水位作为水动力的边界条件。运动方程边界可以指定定量值或者梯度值。

1.2.1 浅水方程

二维的浅水方程的动量方程(仅给出u方向，即水平方向)和连续方程的微分形式如下：

(1)

(2)

式中上面短线代表平均值，方程(2)中Txx、Txy分别为粘滞摩擦力和紊动摩擦力,省略的v方向方程存在Tyy为对流摩擦力。可以采用基于平均流速梯度的紊动粘滞方程计算：

(3)

1.2.2 床面剪切力

(4)

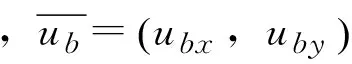
(5)

二维的ub平均水深处的流速计算，阻力系数可根据谢才系数C和曼宁系数M计算：

(6)

1.2.3 泥沙运动控制方程

泥沙运动方程根据水流的对流扩散方程可推导如下：

(7)

泥沙的对流扩散方程根据QUICKEST格式[9]再推导的三阶显式有限差分ULTIMATE格式[10]计算。

1.3 参数确定

模型可以模拟水流作用下细颗粒(<63 μm )粉沙和淤泥的冲刷、运动和淤积。为了精确地模拟泥沙的冲刷过程，床面特意添加了固结层和半固结层，冲刷和淤积均以床面剪切力进行判别。模型中涉及的主要参数有：泥沙颗粒沉速，悬浮泥沙浓度，水平流速，垂向流速，悬沙断面分布形式和临界冲刷淤积剪切力。

1.3.1 淤积和冲刷

模型中添加有随机系统以体现泥沙淤积的随机性，所以淤积公式为：SD=wscbpd，式中ws为泥沙颗粒沉速，m/s；cb为近底含沙量，kg/m3；pd为泥沙淤积几率。淤积几率pd可表示为：

pd=1-τb/τcd,τb≤τcd

( 8)

式中τb为床面剪切力，N/m2；τcd为临界淤积床面剪切力，N/m2。

泥沙方程通过有水动力计算出的床面剪切力来描述。床面剪切力根据对数流速分布以及床面阻力高度可表示为：

τb=ρfcV2/2

(9)

τb为床面剪切力,N/m2；ρ为流体密度，kg/m3；V为平均流速,m/s；fc为水流阻力系数，可根据经验公式计算：

(10)

h为水深,m；k为床面阻力高度,m。

床面冲刷分为固结层的冲刷和半固结或者不固结层的冲刷。

对于固结冲刷(SE)：

(11)

式中E为单位面积时间冲刷系数,kg/(m2·s-1)；τb为床面剪切力，N/m2；τce为临界冲刷床面剪切力,N/m2；n冲刷指数系数,一般取1。

对于半固结或者不固结层的冲刷：

(12)

1.3.2 泥沙颗粒沉速

细颗粒泥沙的沉速取决于泥沙颗粒，絮凝，温度，悬浮物浓度和有机物含量。如今一般存在2组沉速机理：沉速随着泥沙浓度增加而增加和沉速随着泥沙浓度增加而减小。后者主要与泥沙的沉降的阻滞作用有关，大多数河口符合前者。模型中只定义定常值沉速0.0001m/s。

1.3.3 浓度剖面形式

(13)

2 模型计算

数值模型平面布置、范围及床面高程如图1所示，河道上游分为南支和北支两汊，下游相汇。数值水槽总长240 km，中间江心洲105 km，进出口河道宽15 km，分汊河道宽7.5 km。底床床面为上游-5 m到下游-7.8 m的矩形断面斜坡，河床等深线如图1所示。北支设有长105 km和宽400 m的航道，以及间隔为10 km的对丁坝群N1-N5和S1-S5，初始单个丁坝的尺寸为长1800 m，宽200 m。最大网格长度800 m，最小网格长度200 m，如图2所示。最小和最大时间步长为0.01 s和30 s，计算时间足够长。

初始丁坝群的计算网格如图2所示，先以数值水槽均匀流率定参数，然后添加泥沙和修改航道整治建筑物尺寸以探讨均匀流作用下河道不冲不淤时的水沙动力变化。采用M2调和正规半日潮潮位作为下游边界条件，计算由均匀流率定出的参数探讨水沙变化规律。

2.1 均匀流验证

上游流量14600 m3/s和下游水位1 m为初始条件计算水槽水动力，其中曼宁系数为常值32 N/m2。计算出的稳定流速场和流速矢量如图3(A)，除进流口和汇流口流速有不同外，其他区域均为均匀流，大小为0.45 m/s。

图1 模型地形和监测断面

图2 模型计算网格

根据式(4)计算床面剪切力为0.27 N/m2。为了保证验证模型中底床不被冲刷所以取冲刷临界剪切力为0.27 N/m2，同时为了保证上游的悬疑质一旦淤积不会被再悬浮所以选择淤积临界切应力也为0.27 N/m2。计算中，取泥沙沉速为常值0.0001 m/s，假设只有一层底床且密度为300 kg/m3和糙率高度为0.001 m。泥沙初始边界条件上游给定泥沙浓度为0.1 kg/m3，下游泥沙浓度0.01 kg/m3。计算出的稳定悬疑质泥沙浓度分布如图3(B)，泥沙浓度从上游往下游分布依次减小。南支和北支悬疑质泥沙浓度基本分布对称，因网格疏密影响使得北支0.08 kg/m3等值线稍长。从图3计算结果来看，上述给出的参数可以为水槽模型进一步的计算提供合理依据。

图3 流场和悬沙浓度分布图

2.2 概化方案设计

航道整治工程有-10 m深航道和丁坝群，其中丁坝长度从初始1.8 km依次每次增加0.2 km至3.6 km。为了探究丁坝坝田区淤积后再减小该汊水量和增大阻力的同时对进流口和汇流口的水沙的影响变化，把坝田区地形增加3 m作为一种计算方案，如图1所示。动力分为上述已经验证的均匀流(流速0.45 m/s)和M2调和的潮位0 m至2 m的正规半日潮。具体计算方案依次为：①丁坝群(丁坝长度0、1.8、2.0、2.2、2.4、2.6、2.8、3.0、3.2、3.4、3.6 km)；②丁坝群(0～3.6 km)&航道(航深10 m)；③丁坝群(0～3.6 km)&坝田淤积(淤积3 m)；④丁坝群(0～3.6 km)&坝田淤积(淤积高度3 m)&航道(航深10 m)。

监测和统计流量和泥沙通量的断面如图1，上游相互对称位置的A断面和B断面模型中称为分汊口，A断面恰好在航道的左顶端处，前断面模型中称为分流口和A断面相距2.5 km。下游断面与上游相似，记为C断面、D断面和后断面，模型中称为出汊口和汇流口。

3 水沙动力响应

分析均匀流作用下航道整治工程对模型水沙动力的影响及分流比和分沙比的变化。通过分析均匀流作用下和潮流作用下分流比及分沙比的相关性，探寻两者的异同。

3.1 均匀流作用下水沙动力响应

图4所示，均匀流作用下随着丁坝长度的增加A断面的泥沙通量逐渐减少，B断面的泥沙通量逐渐增大。C断面和D断面的泥沙通量相比较，D断面增大的幅度大数倍，基本与后断面泥沙通量保持一致。

图4和图5可以得出工况丁坝群和工况坝田淤积的流量和泥沙通量曲线基本重合，工况航道和工况坝田淤积&航道的流量和泥沙通量曲线基本重合。但前2组和后2组工况却有明显的差别，说明航道的开挖对分汊河道的分流和分沙有较大的影响。

3.2 均匀流作用下分流比和分沙比变化

如图4和图5横坐标为丁坝长度与一汊河道宽度的比值，纵坐标为单汊河道流量或泥沙通量与两汊流量或泥沙通量和的比值，定义为分流比和分沙比。

图4 分流比

图5 分沙比

受相对丁坝长度的影响，有工程一汊分流比或分沙比减小，另一汊增大。前后断面的分流比对称性较好，分沙比不然，在两汊道内发生较多泥沙的冲刷或淤积。存在航道的2组工况对分汊河道的分流比和分沙比有较大的影响。

3.3 均匀流作用和潮流作用相关性分析

把均匀流作用下A断面至D断面分流比和分沙比作为x轴和潮流作用下的全部所有分流比和分沙比作为y轴标记如图6。对于分流比，仅有C断面和D断面2个点稍微偏离45°线，说明无论是均匀流作用下还是潮流作用下周期内所有工况断面的分流比一致性非常好。对于分沙比，C断面和D断面分沙比在0.5左右时各工况潮流影响略有不同。整体可总结，正规潮流周期内对分汊河口的影响作用与均匀流作用相当。潮流导致C断面和D断面分沙比的影响值得进一步的深入研究。

图6 潮流和均匀流作用下分流比和分沙比相关性分析

3.4 分流比和分沙比回归分析

由于A断面和B断面的分流比与C断面和D断面的相等，所以仅对前一组断面分流比进行曲线拟合，而分沙比前后两组均进行了曲线拟合。实际河口中由于同时存在多种航道整治工程和多种动力因素，为了提高所得曲线的实用性和指导价值，所以在曲线拟合时选择了所有工况的数据点。具体曲线方程和相关系数如图7、图8和图9所示。

图7 所有工况A断面和B断面分流比拟合曲线

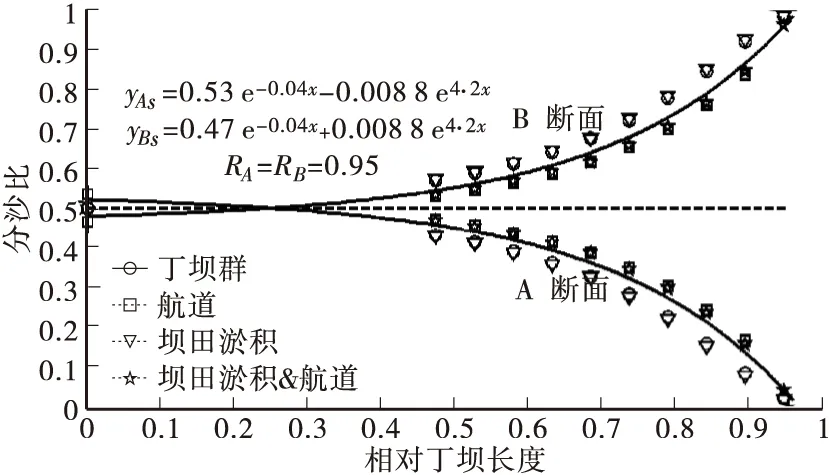
图8 所有工况A断面和B断面分沙比拟合曲线

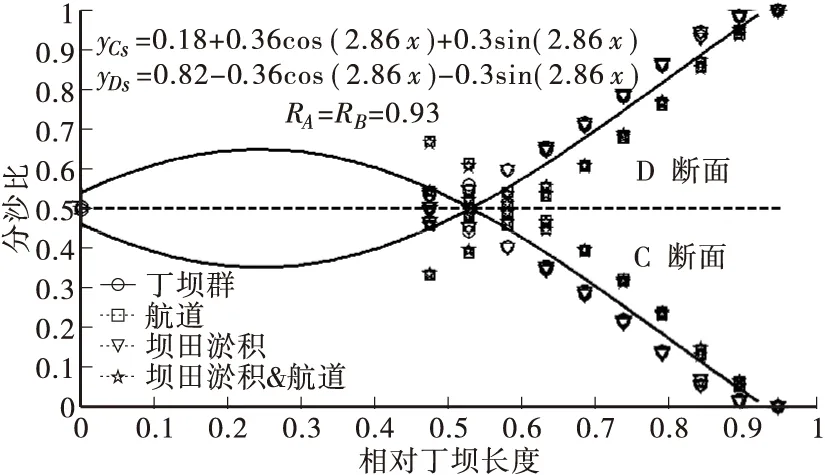
图9 所有工况C断面和D断面分沙比拟合曲线

根据分流比和分沙比的定义可知两式的和应为1并且各项系数应相等。式(14)、式(15)分别为所有工况A断面和B断面分流比与分沙比数据拟合曲线。式(16)为所有工况C断面和D断面分沙比数据拟合曲线。

yAd=0.51e-0.17x-0.00005e9.1x

yBd=0.49 e-0.17x+0.00005 e9.1x

(14)

yAs=0.53e0.04 x-0.0088 e4.2x

yBs=0.47 e0.04 x+0.0088 e4.2x

(15)

yCs= 0.18+0.36cos(2.86x)+

0.3sin(2.86x)

yDs=0.82-0.36cos(2.86x)-

0.3sin(2.86x)

(16)

对式(14)和式(15)曲线进行求导求出相对丁坝长度对应的导数即曲线在该点处的斜率，如图10。分流比随着丁坝长度的增加在小于0.7时曲线斜率缓慢减小，之后指数性减小。分沙比随着丁坝长度的增加接近于线性减小，比分流比的变化快。取斜率-0.5和-1作为判别丁坝长度对两汊河道允许影响的标准得到优良相对长度0.62和极限长度0.78。

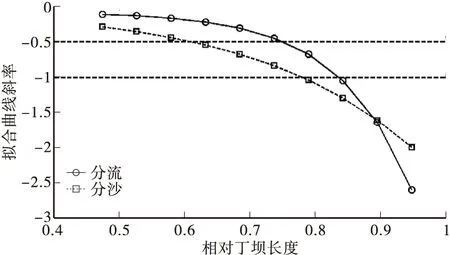
图10 A断面拟合曲线的斜率

4 结论

以明渠均匀流为验证基础，建立分汊河口不同整治工程概化水沙数学模型，探讨均匀流和正规半日潮作用下一汊开挖航道和建设丁坝群后对另一汊河道的水沙动力影响。断面泥沙通量与断面流量变化不一致，存在最优丁坝长度使得断面流量和泥沙通量受丁坝影响较小。断面流量受潮流的影响，距离潮流边界越近受潮流影响越强。均匀流和潮流作用下周期内断面的分流比存在一致性，分沙比在0.5左右时各工况潮流影响略有不同。潮流对汇流处分沙比的影响值得进一步深入研究。对所有工况的分流比和分沙比进行回归性分析，取文中变化幅值参数-0.5和-1作为判别丁坝长度对两汊河道允许影响的指标得到优良相对长度0.62和极限长度0.78。

[1] 张悦, 谈广鸣, 余新明, 等. 丁坝对分汊河道分流比的影响[J]. 中国农村水利水电, 2007(4):91-93.

[2] 余新明, 谈广鸣, 张悦, 等. 分汊河道水沙输移特征试验[J]. 武汉大学学报(工学版), 2007,40(4):9-13.

[3] 窦润青, 郭文云, 葛建忠, 等. 长江口北槽落潮分流比变化原因分析[J]. 华东师范大学学报(自然科学版), 2014(3):93-104.

[4] 童朝锋.分汊口水沙运动特征及三维水流数学模型应用研究[D].南京: 河海大学, 2005.

[5] Amurthur S. Ramamurth, Mysore.G. Satish. Division of Flow in Short Open Channel Branches[J].Journal of hydraulic engineering, 1988, 114(44):428-438.

[6] Amurthur S. Ramamurth, Due Minh Tran, Luis B.Carballada.Division Flow in Open Channels[J].Journal of hydraulic engineering. 1990, 116(3):449-455.

[7] Brian D. Barkdoll, Robert Ertema, A. Jacob Odgaard. Sediment Control at Lateral Divisions: Limit Sand Enhancements to Vane Use[J].Journal of Hydraulic Engineering, 1999, 125(8):362-870.

[8] V. S. Neary, A. Jacob Odgaard. Three Dimensional Flow Structure at Open Channel Divisions[J].Journal of Hydraulic Engineering, 1993, 119(11):1223-1230.

[10] Leonard B P. A stable and accurate convective modelling procedure based on quadratic upstream interpolation[J].Computer methods in applied mechanics and engineering, 1979, 19(1): 59-98.

2017-01-13

国家自然科学基金( 51479122)

吴明珠( 1979-) ，男，工程师，主要从事港口与航道工程研究。

1008-844X(2017)01-0166-06

U 617

A