对中心极限定理的教学研究与思考

李春娥+蒋青松

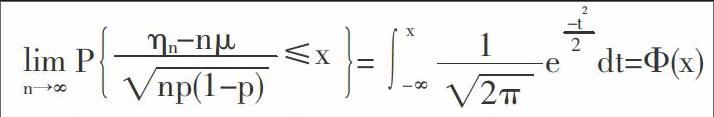
摘 要：中心极限定理是概率论的重要内容之一，又是数理统计中大样本统计推断的理论基础.文章通过贴近学生生活的例子引入中心极限定理，引导学生积极探索问题，解决问题，从而使学生深刻理解中心极限定理内涵、并能灵活运用中心极限定理解决生活中的问题.在教学中，应着重培养学生的学习和研究兴趣，引导他们从学习知识到总结规律，进而向应用推广进行转变.

关键词：中心极限定理 教学研究 总结规律 推广应用

一、中心极限定理的引入

在一定条件下，大量随机变量序列之和的极限分布近似为正态分布的一系列定理，统称为中心极限定理，但是为什么大量的随机变量序列之和的极限分布近似正态分布？对学生而言，非常抽象和难以理解，那么怎么样引入才能引起学习中心极限定理的兴趣和深刻理解、掌握中心极限定理的实质呢？下面以贴近实际生活的例子引入中心极限定理。

引导学生思考问题：以某高校理工科学生的高等数学成绩为随机变量，观察全体学生的高等数学成绩的分布情况，再思考该校自建校以来至今所有学生高等数学成绩之和的分布情况？提出问题以后，让学生分组自由讨论，然后小组代表回答问题，就学生回答的答案进行分析，进而引向中心極限定理。

例：（预算问题）随着大数据的发展，越来越多的人参加数据分析师资格证书的考试，某大型咨询公司今年有500名员工参加此资格证书考试，员工是否通过考试为一随机变量，设每一名员工通过考试的概率为0.8。公司为了鼓励员工积极提升自身素质，若员工通过考试，则给予1000元的奖励。试计算该公司要为这次考试至少做多少元的预算才能以0.95的概率保证通过考试的员工及时领到奖励？

分析：以记500名员工中通过考试的数量，以表示该公司为此次考试准备的预算额，另外，每个员工是否通过考试是相互独立的，则由题意知求：P其中X：B（500，0.8），显然直接用二项分布求Y，计算非常繁琐，难以求出。在此可将随机变量看作由500个两点分布的和构成，那么我们只须求出这些相互独立的大量随机变量的和服从什么分布，问题就得以解决。

由以上分析知，解决问题的关键是求出大量随机变量和的分布，为了得到大量随机变量和的分布情况，引入中心极限定理。

定理1（林德贝格—勒维中心极限定理）设{Xn}是独立同分布的随机变量序列，且E（Xi）=μ，D（Xi）=σ2≥0。

则对任意实数y，有

此定理也称为独立同分布的中心极限定理，即在随机变量序列独立同分布，数学期望和方差存在的条件下，只要充分大，的随机变量之和就近似服从正态分布。

由林德贝格—勒维中心极限定理，把二项分布看作n个两点分布的和，易得二项分布可用正态分布近似，即棣莫弗—拉普拉斯定理。

定理2设随机变量ηn（n=1，2L）服从参数为n，p（0

显然，这是独立同分布中心极限定理的特殊情况，当n→∞时，二项分布的极限分布是正态分布，即可用正态分布来近似地计算复杂的二项分布。

以上两个中心极限定理都是研究可列个相互独立的随机变量和的分布，在一般条件下，当独立的随机变量的个数增加时，随机变量和的极限分布近似服从正态分布，这为利用正态分布来解决随机变量和的问题提供了理论依据。根据两个中心极限定理，以上例题迎刃而解。

思考题：若某高校为了鼓励学生积极考研，对考上重点大学的学生给予2000元的奖励，非重点大学的学生给予1000元的奖励。试通过对母校近几年考研情况的调查，计算学校计财处每年至少做多少元的预算才能以0.99的概率保证考上研究生的同学及时领到奖励。

二、对中心极限定理教学的思考

中心极限定理是学习数理统计的理论基础，在大数据时代，中心极限定理的应用无处不在。如何使学生深刻理解和灵活运用中心极限定理这个重点和难点呢？由于中心极限定理的应用非常广泛，引出定理后，强调其适用的条件和完美的结论，一般不给予证明，因为此定理的证明要用到特征函数，但是大多数教材中没有特征函数这一章节，所以在这儿只强调应用而不是证明。对于统计专业的学生，教师可以从中心极限定理的历史发展过程，结合软件模拟大量随机变量和的分布情况引入，并对中心极限定理进行证明。

三、总结

中心极限定理在概率论与数理统计中是重要的基本理论之一，并且开启了数理统计的学习，在具体的教学实践中，应分析中心极限定理的特征和共性。积极引导学生思考，通过实例教学激发学生的学习兴趣。教学活动以师生互动为主体，对中心极限定理相关部分内容的教学，应遵循学生学习认知规律，循序渐进地开展教学活动，延续“观察分析→理解含义→理论证明→归纳总结→推广应用”这一过程开展相应教学活动，力争让学生达到“学以致用”的目的。

参考文献

[1]陈学慧，赵鲁涛，张志刚.案例式中心极限定理教学研究[J].大学数学.

[2]茆诗松，程依明，濮晓龙.概率论与数理统计教程[M].北京：高等教育出版社.

作者简介

李春娥（1985-），女，山东菏泽人，硕士，讲师。研究方向：应用统计研究。

通讯作者*

蒋青松（1981-），男，湖北潜江人，在读博士，副教授，硕士生导师。研究方向：系统建模与分析及优化，高等数学教学与研究。