从“水仙花数”到哥德巴赫猜想——编程的寻根和延伸

焦华，谢朝东

（1.贵州商学院，贵阳 550014；2.贵州民族大学，贵阳 550025）

从“水仙花数”到哥德巴赫猜想
——编程的寻根和延伸

焦华1，谢朝东2

（1.贵州商学院，贵阳 550014；2.贵州民族大学，贵阳 550025）

从寻找“水仙花数”的编程到验证哥德巴赫猜想的编程，其重心是编程的思考方法，强调知识节点的寻根与拓展，重视由点到面地把握问题的全貌。对基础编程的教学有一定的实用价值，对编程思维的训练有一定的启示。

水仙花数；哥德巴赫猜想；C/C#程序；思维方式

寻找“水仙花数”在很多编程语言教科书上都会提到，因为其中包含有基础编程强调的选择结构与循环结构，是一个较典型的程序范例，具体内容如下：

问题：寻找并打印出所有的“水仙花数”。所谓“水仙花数”是指一个3位数，它的各位数字立方和等于该数自身。例如：153就是一个“水仙花数”，因为153=13+ 53+33。[1]

解法一：利用for循环对100-999之间的所有自然数进行检验，检验的方法用if语句，若判断是“水仙花数”就输出打印，否则就不作为。这里每个数要分解出它的个位、十位、百位。C#程序源代码如下：

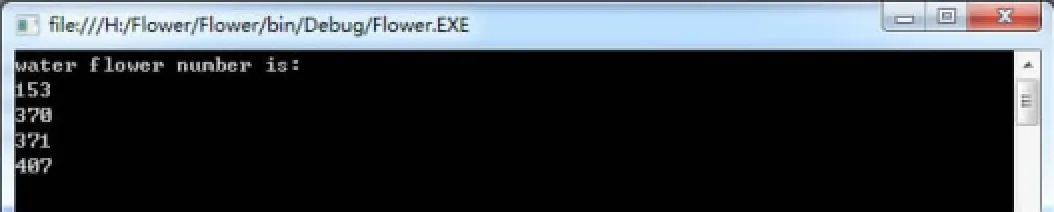
图1

因此“水仙花数”有4个：153、370、371、407。

解法二：思路与解法一相类似，区别在分解出个位、十位、百位的过程。

给出两种解法后，问题已经圆满解决。但学习者通常会有一个疑问：这样的三位数为什么称为“水仙花数”？莫非与水仙花的形状有关？水仙花有六个花瓣、三个花蕊、二层花瓣等，和这些有关联吗？

图2

所有的C/C#程序设计教科书不提这问题，但寻根问底是探索知识的途径！查询资料得到结果整理如下：

“水仙花数”来源于英文“narcissistic number”，英语单词narcissistic是“自我陶醉，自赏的，自恋的”的意思。在古希腊神话中，那喀索斯(narcissus)是河神刻斐索斯与水泽女神利里俄珀之子。他是一个长相非常清秀的美少年，却只爱慕自己的水中倒影，对任何姑娘都不动心。最终在顾影自怜中抑郁死去。他死后化作水仙花，依然停留在水边守望着自己的影子。后来Narcissus就变成为“孤芳自赏者”、“自我陶醉者”的代名词。所以“水仙花数”也称为“自恋数”、“自幂数”。

上面是寻根思维的结果，之后是延伸拓展的思考，还有其他解法吗？有三位的“自幂数”，还有更高位的“自幂数”吗？前面的两种解法是将三位数作个位、十位、百位的分解，现在反过来，个位、十位、百位是由0、1…9组成的，由它们组合得到三位数。于是得到下面的解法。

进一步延伸拓展，“水仙花数”是三位的“自幂数”，还有其他位的“自幂数”吗？

根据数学定义：自幂数是指一个很特别的n位数，它的每个位上的数字的n次幂之和等于它自身。(例如:当n=3时，有153=13+53+33，153即是n=3时的一个自幂数。同理当n=4时，有1634=14+64+34+44，从而1634即是n=4时的一个自幂数。)

自幂数包括：“独身数”、“水仙花数”、“四叶玫瑰数”、“五角星数”、“六合数”、“北斗七星数”、“八仙数”、“九九重阳数”、“十全十美数”。它们是根据位数来划分的，“水仙花数”只是自幂数中的一种。下面列表加以说明：

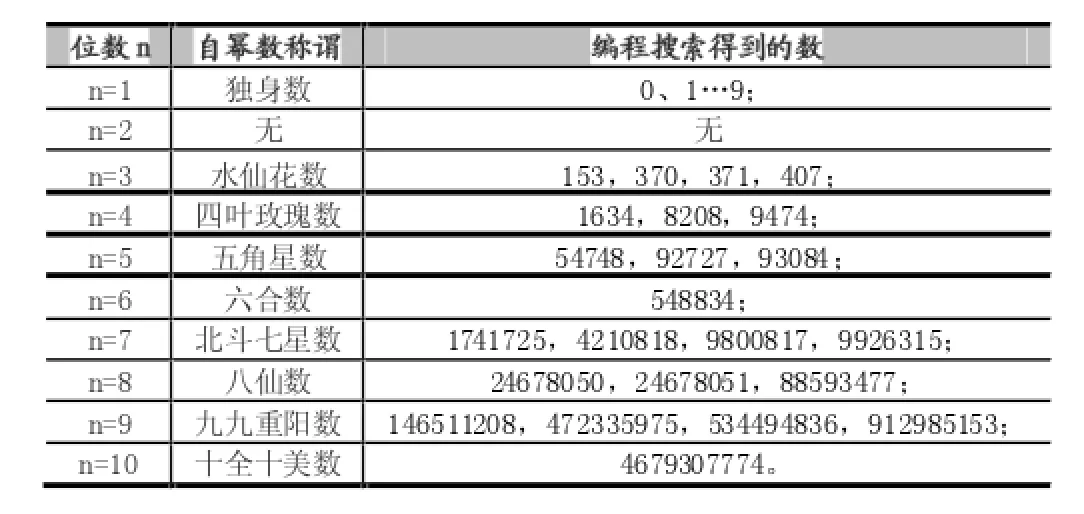
表1

更高位的自幂数编程搜索方法与“水仙花数”的三种解法相类似，但分解出的位数会更多或嵌套的层数会更多，现在提出一个问题：最大的自幂数是多少？计算机数系是有限的，编程害怕无穷大“∞”，在此不再讨论。以下再分析一个特色程序：

问题：验证任意大于2的偶数可分解为两个素数之和并输出这两个素数。

C语言源程序代码如下：[4]

图3

程序注释部分提到C语言的语法：函数定义、函数调用、函数声明；程序找到了每一偶数的所有可能的素数分解。但人们是怎么发现这个重要结论的？

问题寻根：这是世界三大数学猜想之一的哥德巴赫猜想。三大猜想是指费尔马猜想、四色猜想及哥德巴赫猜想。费尔马猜想经过人类350年的努力于1994年由英国数学家安德鲁·怀尔斯证明，遂后称为费尔马大定理；四色猜想经过人类124年的努力于1976年由美国数学家阿佩尔与哈肯借助计算机证明，遂后称为四色定理；哥德巴赫猜想经过人类275年的努力至今尚未解决，目前最好的成果于1966年由中国数学家陈景润取得（陈氏定理）。这三个问题的共同点就是题面简单易懂但内涵却深邃无比，影响了一代又一代的数学家。

延伸拓展：欧拉版本的哥德巴赫猜想是：任一大于2的偶数都可写成两个素数之和。

我们从4=2+2、6=3+3、8=3+5、10=3+7=5+5、……、100=3+97=11+89=17+83=29+71==41+59=47+53、……这些具体的分解中，可以得到哥德巴赫猜想是成立的。甚至有人逐一验证了3300万以内的所有偶数，竟然没有一个不符合哥德巴赫猜想的。进入20世纪、21世纪，随着计算机技术的高速发展，数学家们发现哥德巴赫猜想对于更大的数仍然成立。但是自然数是无限的，谁也不知道会不会在某一个足够大的偶数上，突然出现哥德巴赫猜想的反例呢？275年过去了，哥德巴赫猜想至今尚未解决，数学家们把它比喻为“数学王冠上的明珠”……三大猜想都涉及到无穷大“∞”问题，难怪数学家称无穷大“∞”是个魔鬼！

编程的寻根和延伸就像从一棵树的枝节出发，找到主干、找到根、找到分枝、找到树叶……相当于遍历一棵树，遍历的方式可以不同。因为只有遍历才能认识一棵根深叶茂的参天大树！从而避免“盲人模象”那种“以点代面、以偏概全”的错误！在思维方式上应是线性思维（形式逻辑）与非线性思维（辩证逻辑）的结合。

[1]谭浩强.C程序设计（第四版）[M].清华大学出版社，2010.

[2]陈强.C#编程新手自学手册[M].机械工业出版社，2012.

[3]周洪安.21天学通C#[M].电子工业出版社，2009.

[4]梅创社.C语言程序设计[M].北京理工大学出版社，2010.

From Narcissistic Number to the Goldbach Guess,Seek Roots and Extension of Programm ing

JIAO Hua1，XIE Chao-dong2

（1.Guizhou University of Commerce，Guiyang 550014；2.Guizhou University for nationalities，Guiyang 550025）

From the search for narcissistic number programming to verify Goldbach guess programming,the focus is the thinkingmethod of program-ming,emphasizes seek roots and extension of knowledge node,pays attention to grasp the whole picture of the problem from the point to the surface.Ithas some practical value to the teaching of basic programming,and has some enlightenment to the training of programming thinking.

Narcissistic Number;Goldbach Guess;C/C#Program;Thinking Mode

1007-1423（2017）12-0011-04

10.3969/j.issn.1007-1423.2017.12.003

焦华（1964-），男，贵州贵阳人，硕士研究生，副教授，研究方向为算法与程序

2017-02-28

2017-04-20

贵州省教育厅2016年本科教学工程项目（No.121）

谢朝东（1963-），男，贵州毕节人，硕士研究生，教授，研究方向为偏微分方程