双镜头航空相机投影转换误差分析
周海岸 黄巧林 林招荣 刘秀
双镜头航空相机投影转换误差分析
周海岸 黄巧林 林招荣 刘秀
(北京空间机电研究所,北京100094)
双镜头双探测器拼接式航空摄影相机获取的是双中心投影影像,需要将其转换成等效单中心投影虚拟影像并控制其转换精度。文章对双镜头相机建立由双中心投影向等效单中心投影转换的数学模型,依据模型得出投影转换误差的影响因素,并采用蒙特卡罗方法与最大误差方法对投影转换误差进行MATLAB仿真,利用仿真结果分析总体误差分布与各误差源的影响效果,为误差源的范围限制提供参考。结果表明:对于参数特定的双镜头航空相机,当主点误差限为0.5像元,主距误差限为1像元,相对角元素误差限为10″,相对线元素误差限为1mm,相对航高误差限为150m时,投影转换误差可控制在2像元内,且相对角元素误差为主要误差源。
双镜头 投影转换 误差仿真 蒙特卡罗方法 航空相机
0 引言
航空数字相机在地形制图、灾害监测、城市管理、资源调查等方面广泛应用,然而单面阵数字相机只能获取小区域影像,难以满足大范围成图要求。为了扩大视场角,同时提高影像几何精度,可以采用双镜头、双探测器拼接而成的航空数字相机。双镜头相机曝光时生成的是双中心投影影像,需要将其转换成等效单中心投影,将不同探测器影像拼接生成大幅面虚拟影像,以方便后续处理。研究者从不同角度分析了拼接式相机的虚拟影像生成[1-5]。从投影转换的角度,文献[6-8]提出了改进的投影转换方法以生成拼接图像,其中转换系数由在轨自检校获取;文献[9-10]在文献[11]研究的基础上构建了利用多个面阵CCD影像合成大像幅、单中心投影数字航空影像的误差模型,详细分析了由于地面起伏和相邻镜头中心距引起的投影转换误差;文献[12-13]建立了内视场拼接型数字航测相机几何特性描述模型,综合考虑了内方位元素误差、物镜光学畸变、多面阵CCD不平行性误差及安装误差对转换误差的影响;文献[14]提出顾及子影像拼接误差的自检校成像模型,利用该模型进行光束法区域网自检校空三数据平差处理,可得稳定可靠的子影像拼接参数估值解;文献[15]在讨论多视场遥感图像拼接误差时,将成像几何模型简化为由共线条件方程表示的卫星本体坐标系到像空间坐标的转换过程,得出拼接误差的主要误差源。
由于投影转换的误差分析主要集中于近似的模型误差或由试验验证所得,未有针对误差源具体数值的仿真分析,因此本文将重点研究影像由双中心投影向等效单中心投影转换的数学模型所涉及到的参数对误差的影响。分析采用的是成图比例尺为1∶500的双镜头正视航空摄影相机,两组镜头均采用相同的光学系统,对应相同的CMOS探测器组件,镜头主光轴平行,探测器共面,平行度与共面度的精度要求较高。
1 投影转换的数学模型
由大视场面阵相机的双中心投影构建等效单中心投影虚拟影像,其实质是寻求一个统一基准的虚拟影像坐标系,通过建立严密的反映双探测器相对方位关系的模型,实现双中心投影影像向统一坐标系下的投影转换,进而通过高精度匹配和自检校等影像处理流程实现等效单个大幅面虚拟影像的生成。
选择某单个探测器的影像作为基准影像,以其像平面坐标系作为虚拟像平面坐标系,以提供一个承影面,使双探测器重叠区内(如图1灰色条形区域)所有同名点对之间的总体位置偏差最小。除基准探测器之外的探测器获取的影像依据相对于基准影像的方位关系将像点坐标转换至的坐标基准内,于是基准影像与转换之后的影像共同生成等效单中心投影虚拟影像(如图1所示)。此外,为了描述像点在空间的位置,需要将二维虚拟像平面坐标系转换成三维虚拟像空间坐标系。虚拟像空间坐标系用于表示虚拟影像上各像元在像方空间的位置。如图2所示,影像与影像分别为沿轴方向(即垂直飞行方向)组装的双镜头相机所摄取的影像。以影像的摄影中心为原点,沿影像面轴方向为轴方向,从像主点指向摄影中心方向为轴,采用右手坐标系建立轴,得到虚拟像空间坐标系,影像的摄影中心即为虚拟影像的等效单中心。
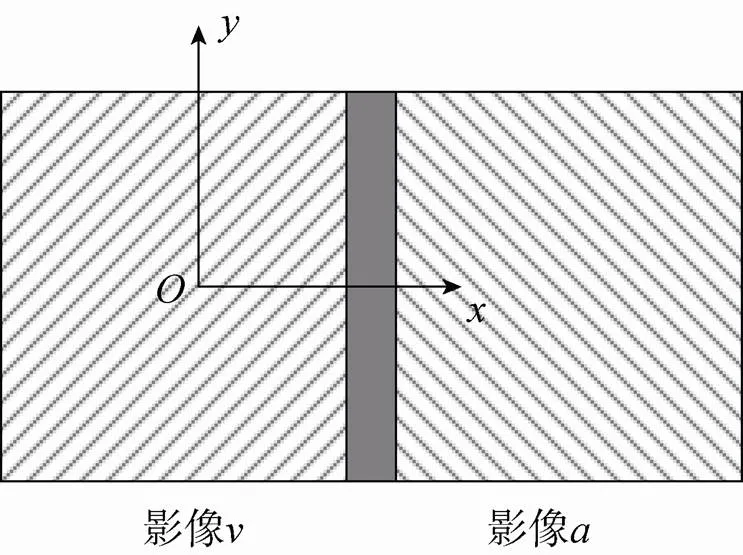
图1 虚拟像平面坐标系与虚拟影像
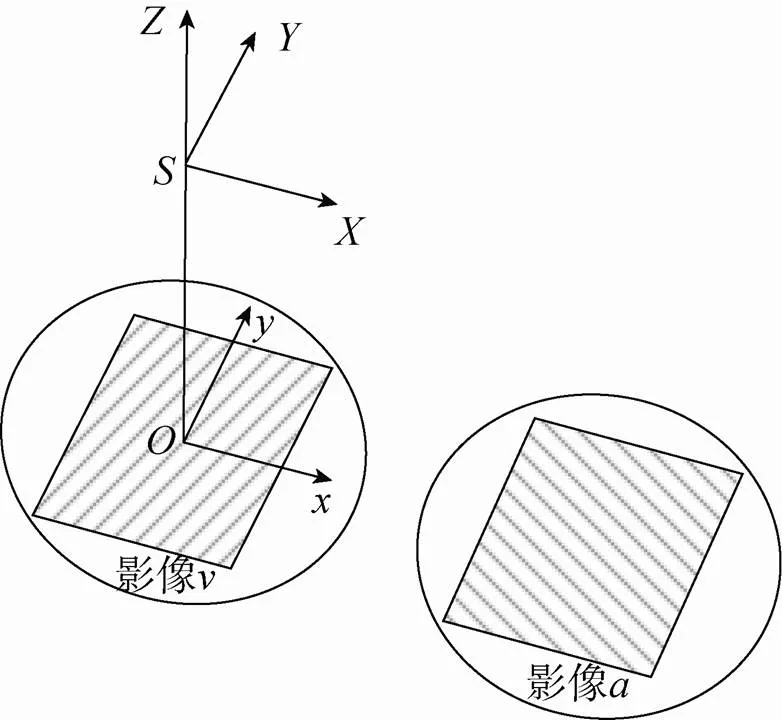
图2 虚拟像空间坐标系
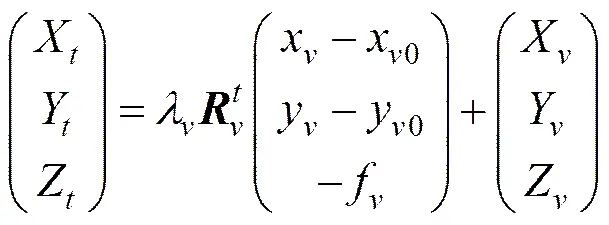
(2)
联立式与式可得
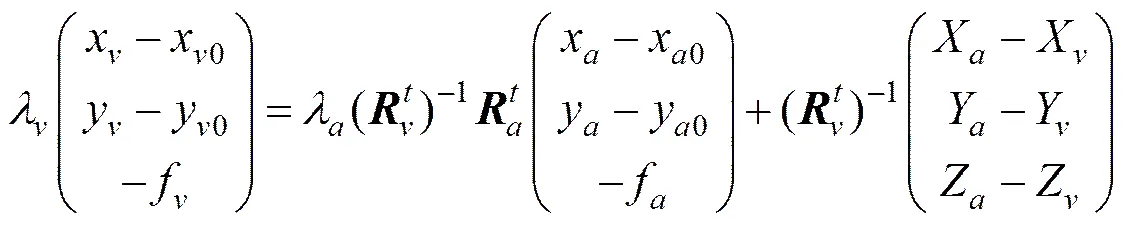
式(3)即为待转换影像与基准影像间的相对方位关系式。当位于影像像空间坐标系中的任意像点转换至基准影像的像空间坐标时,需经过旋转矩阵与平移向量。
令

同时令
(5)
则式可改写为
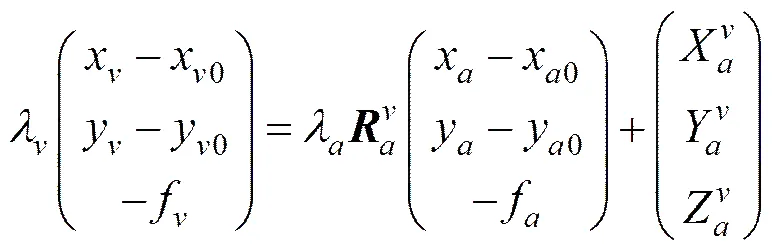
(7)
式中
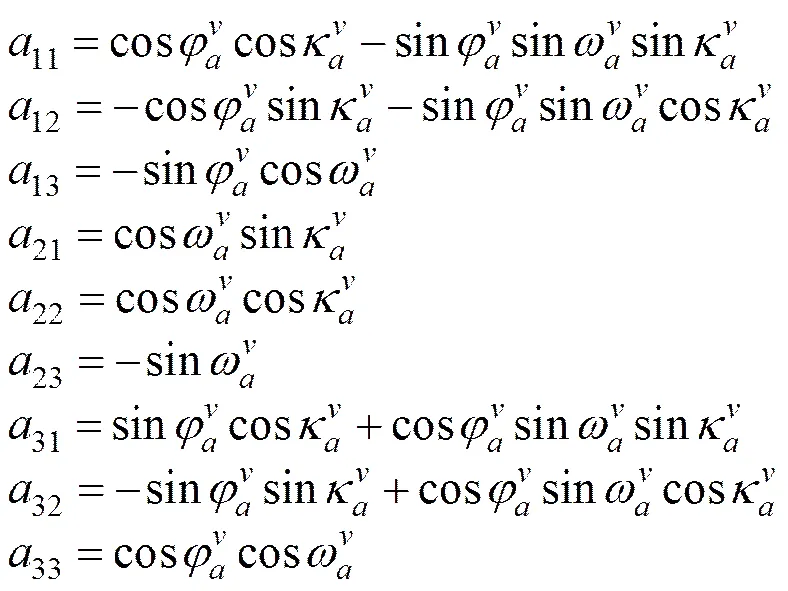
在经过实验室检校、控制场检校与在轨自检校得出影像内方位元素、畸变元素与相对外方位元素的数值后,根据式(6)可得
(8)
式(8)即为目标点虚拟影像像素所对应的待转换影像像点坐标,即由双中心投影向等效单中心投影转换的数学模型。
2 投影转换的误差分析
2.1 投影转换误差模型
由式(8)可以看出由双中心投影向等效单中心投影转换时的待转换像点坐标与等参数有关

在理想情况下,各参数误差为0,通过式(8)可以计算出准确的待转换影像像点坐标,将影像重采样获取的灰度值赋给虚拟影像目标点像元。但检校过程中解算的内外方位元素与地形起伏引起的相对航高均存在误差,因此计算得出的坐标与理想坐标有偏差,偏差值即为投影转换误差。
根据非线性函数的误差传播定律,假设各参数误差相互独立,则投影转换误差与各参数误差的关系为
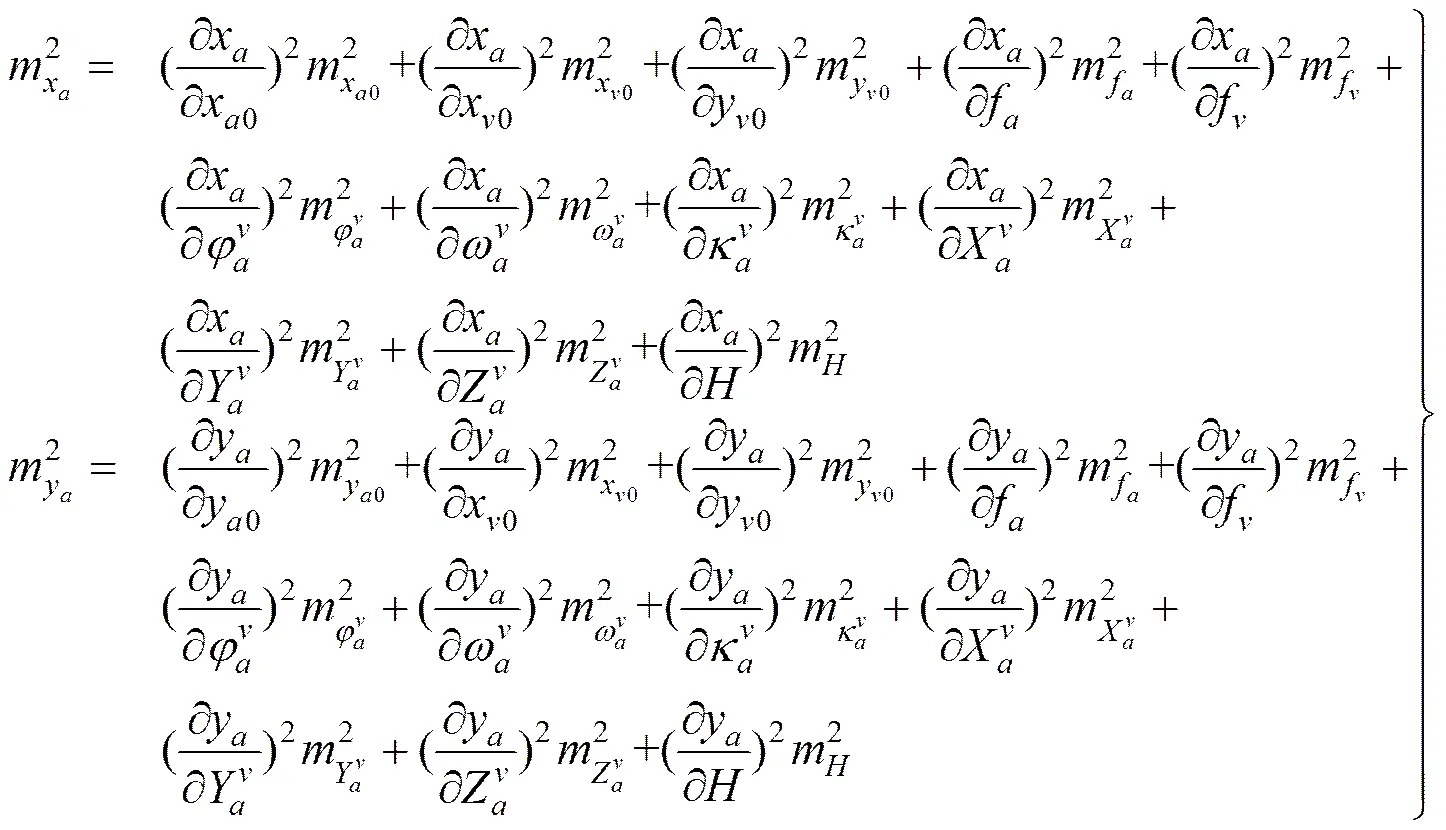
式(10)即为由双中心投影向等效单中心投影转换的误差模型,由于全微分很复杂,故下文将采用蒙特卡罗方法与最大误差方法,基于MATLAB平台仿真分析由双中心投影向等效中心投影转换的误差。
2.2 投影转换误差仿真
设相机系统参数中像元尺寸为6μm´6μm,基准探测器与待拼接探测器的焦面像元数均为10 000´10 000,即像幅尺寸均为0.06m´0.06m;主距均设为0.15m,主点坐标均设为(0.003m,0.003m),两组镜头平行度设为1°,即相对角元素名义值为1°;基准影像与待拼接影像间的基线长设为0.15m,即相对线元素(轴方向)名义值为0.15m,由于安装误差的影响,相对线元素与名义值设为0.01m。依据现有的摄影测量相机的检校精度[16-19],其余各参数的名义值、极限误差设定与误差分布见表1。根据地形图航空摄影规范(GB-T 6962-2005),当航摄比例尺小于1∶7 000时,航摄分区内的地形高差不得超过1/4的相对航高[20];设基准航高为1 200m,则地形最大高差为300m,相对航高范围为1 050~1 350m。以待拼接影像中心点作为目标点,即取虚拟影像平面坐标,分别采用蒙特卡罗方法与最大误差方法进行误差分析。
表1 各参数名义值、极限误差及误差分布
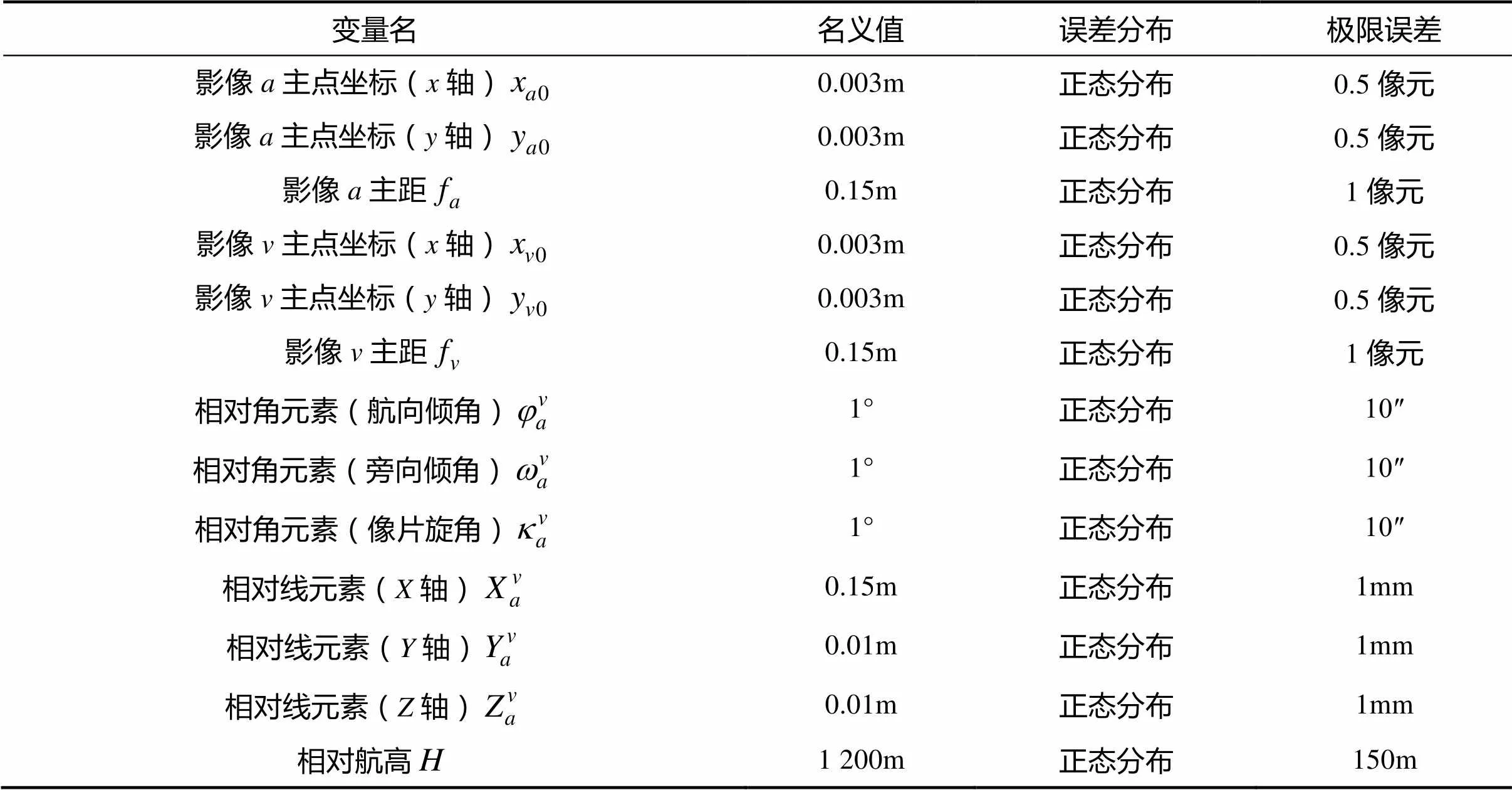
Tab.1 The nominal value, limit error and its distribution of each parameter
(1)蒙特卡罗方法
应用蒙特卡罗方法进行MATLAB仿真的步骤如下:
1)启动并初始化应用程序;
2)将各参量设为名义值,运行式(8)待转换像点坐标函数得到像点坐标初始值,保存其数据;
3)运用Randn函数,生成各参量长度为100 000的伪随机数列,其分布服从正态分布,均值为名义值,方差为1/3的极限误差值(取置信水平为99.75%);
4)将各参量的伪随机数列与名义值相加得到新的自变量数列,根据蒙特卡罗方法,运行式(8)生成引入误差的像点坐标数列;
5)将4)所得的数列与2)所得的初始值相减,即为像点坐标误差数列,统计计数生成误差分布直方图。
图3为运用蒙特卡罗模拟仿真生成的轴、轴方向投影转换的误差分布。从图中可以看出,轴、轴方向的投影转换误差近似服从均值为0的正态分布,且轴方向误差分布较为松散。仿真得出轴方向误差的均值和方差分别为,,轴方向误差的均值和方差分别为,,即置信水平为99.75%时,,,轴方向最大误差约为1.7像元,轴方向最大误差约为1.5 像元。
(a)轴方向
(a)-axis direction
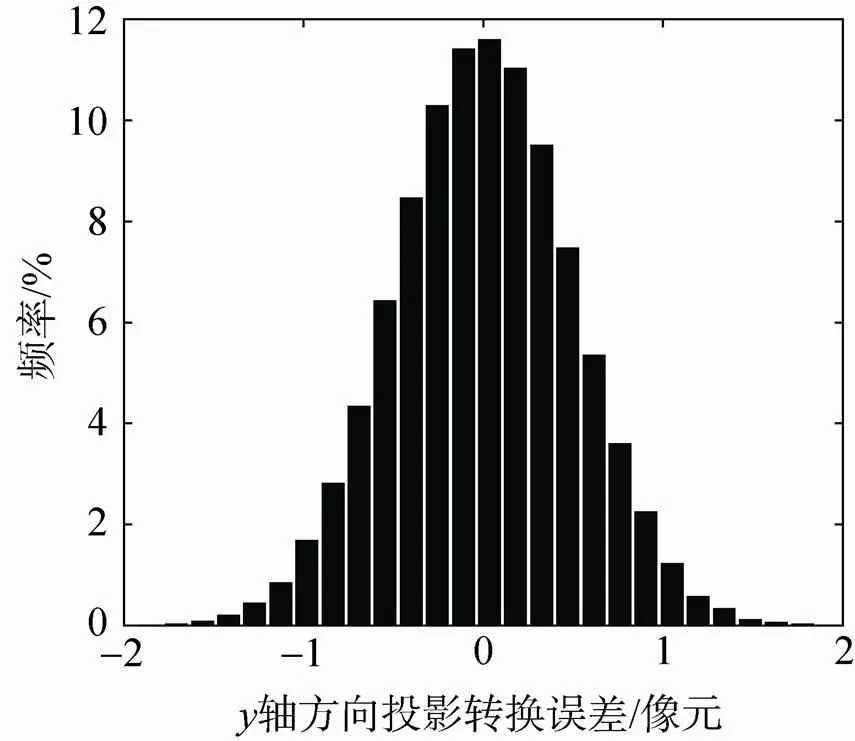
(b)y轴方向
(2)最大误差方法
以轴方向为例,分析单一参数误差对投影转换误差的影响。设单一参数误差限取表1中的极限误差值,其它参数误差设为0,投影转换误差随主点误差、主距误差、相对角元素误差、相对线元素误差与相对航高误差的影响曲线分别如图4(a)~(e)所示。从图中可以看出,基准影像与待拼接影像的内方位元素误差对投影转换误差的影响分别呈正相关与负相关,作用过程中可能相互削减。此外相机主点误差控制在0.5像元、主距误差控制在1像元时,投影转换误差均小于0.5像元;相机间相对角元素误差控制在10″时,投影转换误差约为1.5像元;相对线元素误差控制在1mm时,投影转换误差近似为0,可以忽略;相对航高误差引起的投影转换误差约为0.4像元。
(a)主点误差的影响
(a)Influence of main point error
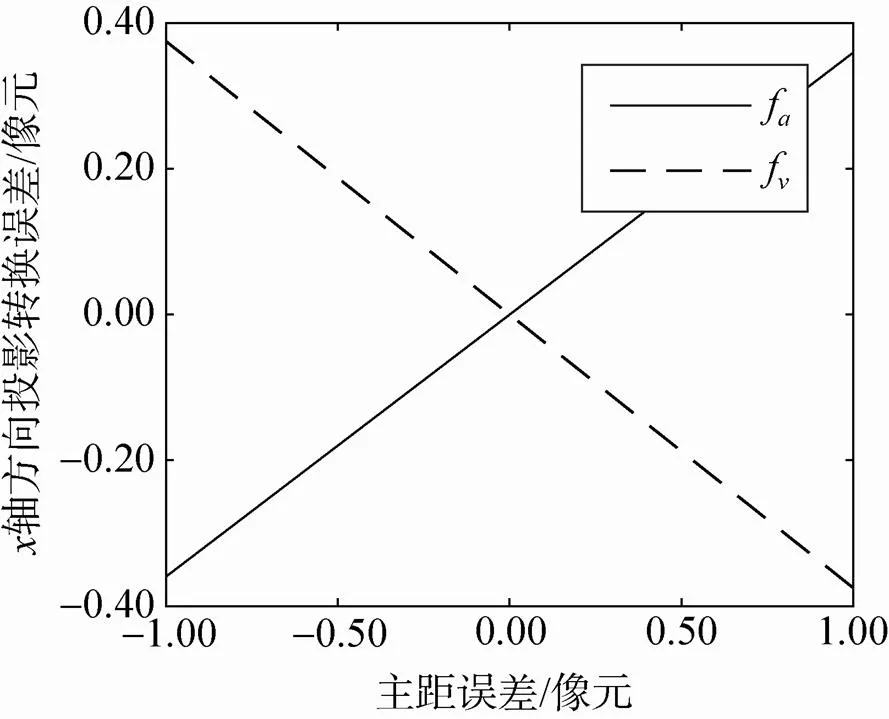
(b)主距误差的影响
(b)Influence of principal distance error
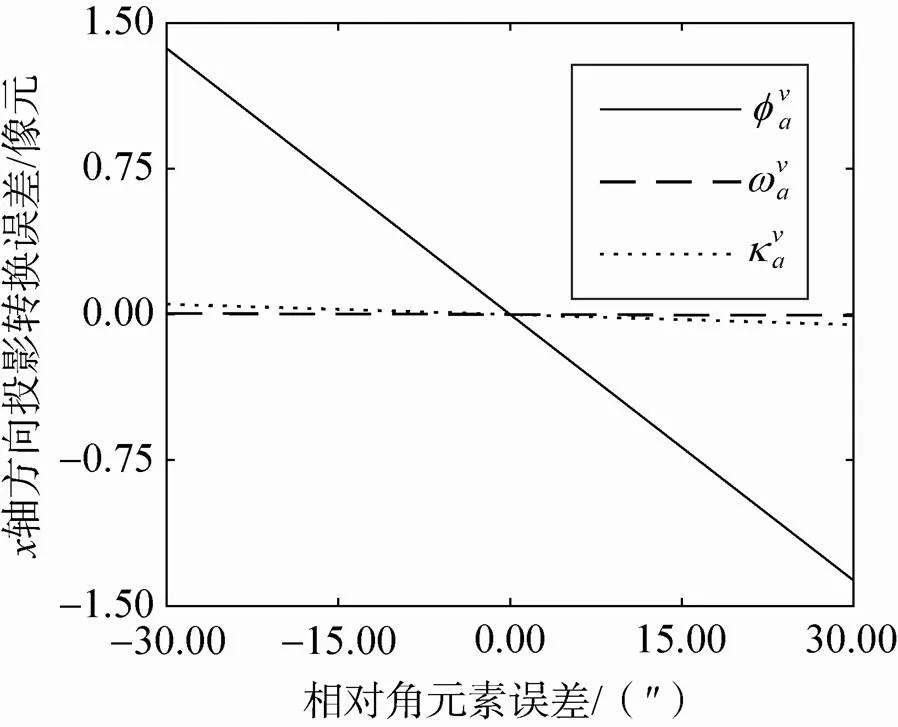
(c)相对角元素误差的影响
(c)Influence of relative angle element error
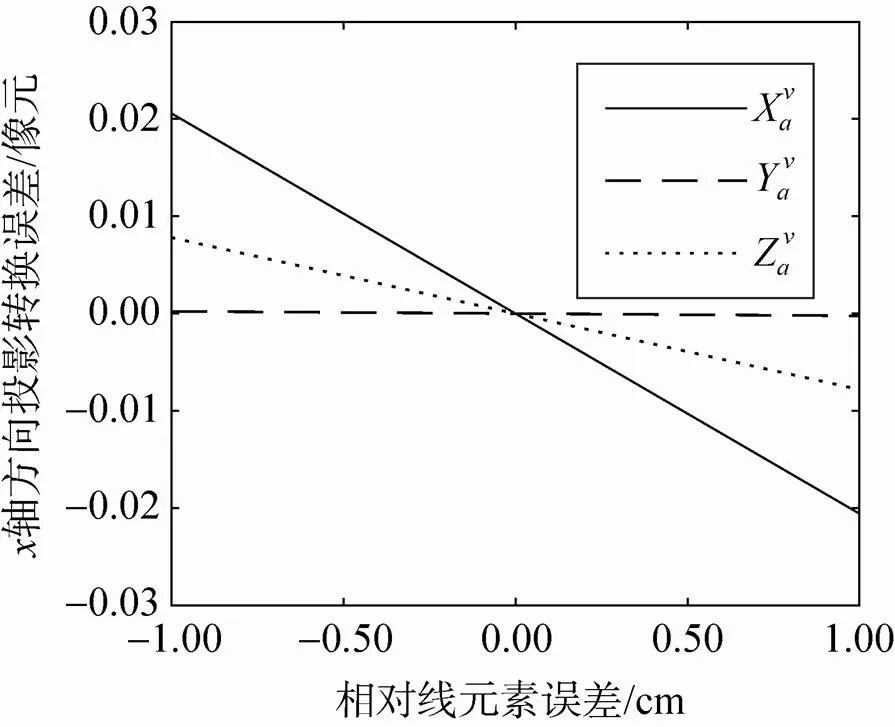
(d)相对线元素误差的影响
(d)Influence of relative line element error
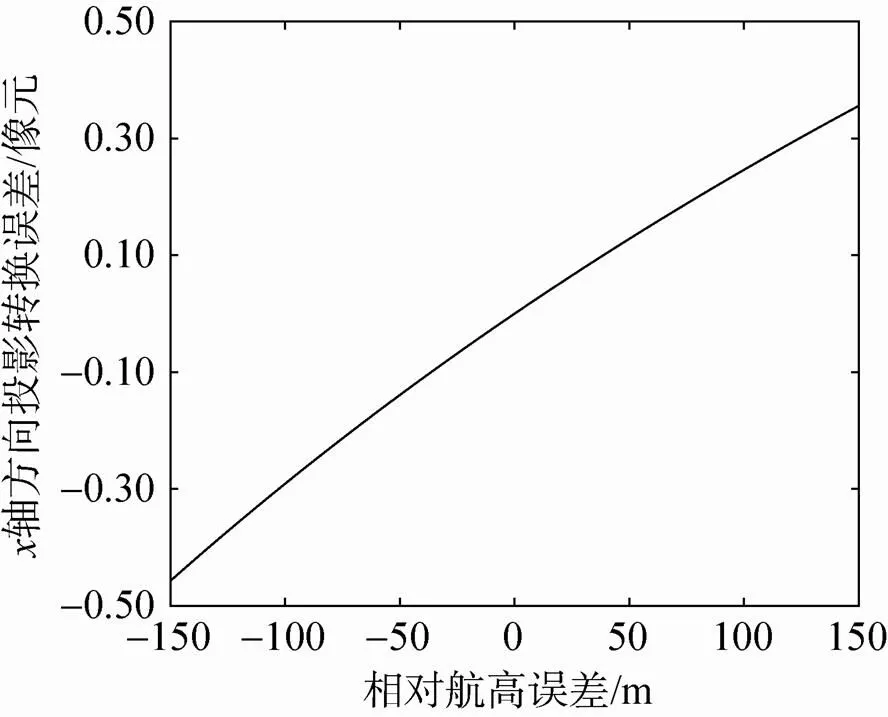
(e)相对航高误差的影响
图5给出了由MATLAB仿真数值绘制出的当各单一变量取最大误差时对应的轴、轴方向投影转换误差。不同参量对轴、轴方向的误差影响并不相同。对于轴方向,除相对航向倾角的误差影响较为显著外,待拼接影像与基准影像的主点主距误差、相对航高误差对投影转换误差的影响处于同一数量级,近似为0.5像元。对于轴方向,除相对旁向倾角的误差影响较为显著外,待拼接影像与基准影像的主点误差、相对像片旋角误差对投影转换误差的影响均近似为0.5像元,其它因素可以忽略。

图5 各变量最大误差对应的投影转换误差
根据以上两种方法的仿真结果可以得出,除了属于外界环境的相对航高误差之外,当相机的检校误差控制在一定范围之内时,如主点误差限为0.5像元,主距误差限为1像元,相对角元素误差限为10″,相对线元素误差限为1mm,影像的投影转换误差约为2像元。
3 结束语
本文对双镜头相机建立了由双中心投影向等效单中心投影转换的数学模型并对投影转换误差进行了分析。误差分析方法中,蒙特卡罗方法直观体现出各参量取正态分布的随机数时投影转换误差的总体分布情况,利用仿真得出的均值和方差可计算出满足特定置信水平时的误差限;最大误差方法分析了各误差源单独作用时的投影转换误差。通过两种方法的综合运用,可调整不同误差源参量的误差范围,以满足一定的投影转换误差的限制要求;对于影响较大的误差源,如内方位元素误差、相对角元素误差,需要重点控制误差限,而对于相对线元素误差,则可以适当放宽误差限;同时各参量误差范围的制定也为方位元素的检校精度提供了参考。
此外,本文的研究仍有以下几点需要改进:
1)在投影转换的表达式中未考虑镜头畸变,事实上,经过检校后畸变不能完全校正,影像边缘可能仍然存在少量残余畸变;
2)相对航高误差与地形有关,模拟的高差不能准确反应实际地形;
3)各参量的检校误差并非完全相互独立,仿真中未考虑各参量误差之间的相关性。
在后续研究中可综合考虑以上因素,以提高投影转换的模型精确度,并用试验对误差加以验证,完善投影转换误差的仿真分析。
(References)
[1] LU Y, WANG K, FAN G. Photometric Calibration and Image Stitching for a Large Field of View Multi-Camera System[J]. Sensors, 2016, 16(4): 516.
[2] SUN T, FANG J, ZHAO D, et al. A Novel Multi-digital Camera System Based on Tilt-shift Photography Technology[J]. Sensors, 2015, 15(4): 7823-7843.
[3] PETRIE G. Systematic Oblique Aerial Photography Using Multiple Digital Cameras[J]. Photogrammetric Engineering & Remote Sensing, 2009, 75(2): 102-107.
[4] 胡海彦, 杨韫澜, 方勇, 等. DMZ内视场光学分割型航摄相机子影像高准确度几何拼接[J]. 光子学报, 2015, 44(4): 140-147. HU Haiyan, YANG Yunlan, FANG Yong, et al. High Accuracy Sub-images Stitching for DMZ Airborne Camera in Kind of Optical FOV Splitting[J]. Acta Photonica Sinica, 2015, 44(4): 140-147. (in Chinese)
[5] 刘凤英, 王冬. 自稳定双拼相机影像拼接技术[J]. 测绘通报, 2012(2): 56-58. LIU Fengying, WANG Dong. The Self-stablized and Dual-combined Camera Image Mosaic Technology[J]. Bulletin of Surveying and Mapping, 2012(2): 56-58.(in Chinese)
[6] RAU J Y, JHAN J P, RAU R J. Semiautomatic Object-oriented Landslide Recognition Scheme from Multisensor Optical Imagery and DEM[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 1336-1349.
[7] RAU J Y, JHAN J P, HSU Y C. Analysis of Oblique Aerial Images for Land Cover and Point Cloud Classification in an Urban Environment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(3): 1304-1319.
[8] RAU J Y, JHAN J P, LI Y T. Development of a Large-format UAS Imaging System with the Construction of a One Sensor Geometry From a Multicamera Array[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(10): 5925-5934.
[9] 王慧, 吴云东, 张永生. 面阵CCD数字航测相机影像几何拼接误差模型与分析[J]. 测绘学院学报, 2003, 20(4): 257-262. WANG Hui, WU Yundong, ZHANG Yongsheng. Modeling and Analyzing of Geometric Joint Error for CCD Matrix Images of Digital Aerial Camera[J]. Journal of Institute of Surveying and Mapping, 2003, 20(4): 257-262.(in Chinese)
[10] 王慧. 面阵CCD航测相机成像模型与处理技术[D]. 郑州: 解放军信息工程大学, 2006. WANG Hui. Imaging Model and Processing of Large Format CCD Aerial Camera[D]. Zhengzhou: PLA University of Information Engineering, 2006.(in Chinese)
[11] TANG L, DÖRSTEL C, JACOBSEN K, et al. Geometric Accuracy Potential of the Digital Modular Camera[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 33(B4/3;PART 4): 1051-1057.
[12] 方勇, 崔卫平, 马晓锋, 等. 单镜头多面阵CCD相机影像拼接算法[J]. 武汉大学学报(信息科学版), 2012, 37(8): 906-910. FANG Yong, CUI Weiping, MA Xiaofeng, et al. Image Stitching Algorithm of Digital Camera with Single Field Lens and Multiple Area CCD[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8): 906-910.(in Chinese)
[13] 陈巍然, 方勇, 孙赫, 等. 多面阵摄影相机影像特征匹配算法[J]. 测绘科学与工程, 2014, 34(3): 1-4. CHEN Weiran, FANG Yong, SUN He, et al. Feature Matching Algorithm for Multi-array Camera Image[J]. Geomatics Science and Engineering, 2014, 34(3): 1-4.(in Chinese)
[14] 杨韫澜, 韩玲, 胡海彦, 等. 顾及子影像拼接参数的自检校模型[J]. 测绘通报, 2014(10): 29-32. YANG Yunlan, HAN Ling, HU Haiyan, et al. Self-calibration Model Considering Stitching Parameters of Sub-image[J]. Bulletin of Surveying and Mapping, 2014(10): 29-32.(in Chinese)
[15] 岳春宇, 何红艳, 鲍云飞, 等. 多视场遥感图像虚拟焦面拼接理论误差分析[J]. 航天返回与遥感, 2015, 36(2): 60-68. YUE Chunyu, HE Hongyan, BAO Yunfei, et al. Error Analysis of Remote Sensing Image Mosaic Based on Virtual Focal Plane[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(2): 60-68.(in Chinese)
[16] 王冬, 冯文灏, 卢秀山, 等. 基于多片空间后方交会的CCD相机检校[J]. 测绘科学, 2008(4): 64-66.WANG Dong, FENG Wenhao, LU Xiushan, et al. CCD Camera Calibration Based on Space Resection with Multi-image[J]. Science of Surveying and Mapping, 2008 (4): 64-66.(in Chinese)
[17] 王冬红. 机载数字传感器几何标定的模型与算法研究[D]. 郑州: 解放军信息工程大学, 2011. WANG Donghong. A Study on the Mathematic Model and Algorithm of the Geometric Calibration of Airborne Digital Sensor[D]. Zhengzhou: PLA University of Information Engineering, 2011.(in Chinese)
[18] 杨韫澜. 摄影测量自检校技术研究[D]. 西安: 长安大学, 2015. YANG Yunlan. Study on the Self-calibration Technology in Photogrammetry[D]. Xi’an: Chang’an University, 2015.(in Chinese)
[19] 郭忠磊, 赵志勇, 滕惠忠, 等. 无人机影像自检校光束法区域网平差精度分析[J]. 海洋测绘, 2016, 36(2): 75-78. GUO Zhonglei, ZHAO Zhiyong, TENG Huizhong, et al. Precision Analysis of Self-calibration Bundle Block Adjustment for UAV Images[J]. Hydrographic Surveying and Charting, 2016, 36(2): 75-78.(in Chinese)
[20] 国家测绘局测绘标准化研究所. GB/T 6962-2005 1:500,1:1000,1:2000地形图航空摄影规范[S]. 北京: 中国标准出版社, 2005: 1-20. National Bureau of Surveying and Mapping Institute of Surveying and Mapping. Specification for Aerial Photography of 1:500, 1:1000, 1:2000 Scale Topographic Maps, GB/T 6962-2005[S]. Beijing: Standard Press of China. 2005: 1-20.(in Chinese)
(编辑:王丽霞)
Analysis of Projective Conversion Error forDual-Lens Aerial Camera
ZHOU Haian HUANG Qiaolin LIN Zhaorong LIU Xiu
(Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)
It is a double-center projection image that an aerial photographic camera with double-lens and double-sensors obtains. It is necessary to convert them to an equivalent single-center projection virtual image and control the conversion accuracy. This paper establishes a mathematical model of the conversion from double-center projection to equivalent single-center projection for adual-lens aerial camera. According to the model, the influence factors of projective conversion error are obtained. It also simulates the projective conversion error with MATLAB by methods of Monte Carlo and maximum error, analyzes general error distribution and consequence of each error source by utilizing the simulation result, and providing reference for the limits of error sources. The results show that for a dual-lens aerial camera with specified parameters, the projective conversion error could be controlled within 2 pixel if the error margin of principal points is 0.5 pixel, focus distances 1 pixel, relative angle elements 10″, relative line elements 1mm and relative flight height 150m, among which the relative angle element error is the major error source.
dual-lens; projective conversion; error simulation; Monte Carlo method; aerial camera
TP751
A
1009-8518(2017)02-0082-09
10.3969/j.issn.1009-8518.2017.02.011
2016-09-07
周海岸,女,1991年生,2014年获北京航空航天大学飞行器设计与工程(航天工程)专业学士学位,现在中国空间技术研究院飞行器设计专业攻读硕士学位。研究方向为空间光学遥感器总体设计。E-mail:surinran@sina.com。

