基于灰色预测的EWMA成本控制设计

樊树海+姚斌+张雷+季春

【摘 要】 在稳定的制造过程中，伴随着订单和产品型号的变化，单位产品的制造成本应该在稳定的区间内发生变化。对单位产品制造成本进行监控，能够在宏观层面发现制造过程是否存在一次合格率过低或材料消耗异常等情况。为监测单位产品的制造成本，在传统的EWMA控制图基础上，提出了一种基于灰色预测的EWMA控制图。此控制图采用GM（1，1）模型，对单位产品制造成本的波动过程进行建模，验证单位产品制造成本是否出现异常偏移，并且当其因某些原因出现规律性偏移时采用模型对偏移过程进行预测，结合EWMA控制图的上下控制限提供波动的接受范围，当预测值超出上下限应当停止生产查找原因。不同于传统控制图的事后控制，文章提出了一种事前控制的方法。

【关键词】 EWMA控制图； GM（1，1）模型； 灰色預测

【中图分类号】 F270.7 【文献标识码】 A 【文章编号】 1004-5937（2017）09-0023-04

一、引言

自休哈特提出控制图概念以来，出现了较多有效的控制图技术，其中指数加权移动平均（EWMA）控制图就是一种针对较小偏移非常有效的控制图[1]。传统的EWMA控制图主要以上下限为控制标准，本文提出一种基于灰色预测的EWMA控制图，可以更早一步地发现过程中的偏移，并对偏移过程进行预测，进而提出一种新的指南性的EWMA异常判定标准。

二、EWMA控制图

1959年罗伯特（Robert）提出了指数加权移动平均（Exponential Weighted Moving Average，EWMA）图[2]。其基本思想是在充分利用历史数据的基础上，强调当前样本大的重要性，并逐步淡化先前样本所提供的信息。

假设Xi是相互独立的随机变量序列[3]，则EWMA图的统计量表示为：

Zi=λXi+（1-λ）Zi-1

其中，Zi是当前时刻的统计量；Zi-1是上一时刻的EWMA图统计量；Z0=μ，是EWMA图统计量的初始值；λ（0<λ≤1）是权重因子。当λ<0.1时，EWMA控制图对小偏移有更灵敏的反应，但对大偏移有明显的滞后[4]。

由于

Zi=λXi+（1-λ）Zi-1

=λXi+λ（1-λ）Xi-1+…+λ（1-λ）i-1

X1+（1-λ）iZ0

可以证明

E（Zi）=E（Xi）=μ

Var（Zi）=■σ2

单个观察值的中心线、上下控制限分别为：

UCL=μ+3σ■

CL=μ

LCL=μ-3σ■

随着样本数目的增加，统计量Zi的方差Var（Zi）=■σ2趋近于■σ2，上下控制限趋近于直线。

三、GM（1，1）模型

灰色系统理论由我国学者邓聚龙教授在20世纪80年代首次提出[5]。其中一阶微分GM（1，1）预测算法不要求关于数据概率分布的先验知识，是一种较为通用的辨识方法，同时，GM（1，1）算法与自回归算法和支持向量机相比，没有复杂的递推过程，计算量小[6]。

对于时间序列X（0）有n个观察值，X（0）

={X（0）（1），X（0）（2），…，X（0）（n）}，通过累计加成新序列X（1）={X（1）（1），X（1）（2），…，X（1）（n）}，则GM（1，1）模型响应的微分方程为：

■+αX（1）=μ

式中，α称为发展灰度；μ称为内生控制灰数。

设■为待估参数向量，■=αμ，利用最小二乘法求解可得：

α=（BTB）-1BTYn

其中，

B[7]=■

Yn=■

求解该微分方程，可得预测模型为：

■（1）（k+1）=[X（0）（1）-■]e-ak+■

（k=0，1，2，…，n）

由预测模型计算■（1）（i），并将其累减生成■（0）（i），计算■（0）（i）与X（0）（i）的绝对误差序列以及相对误差序列。

Δ（0）（i）=X（0）（i）-■（0）（i）i=1，2，…，n

φ（i）=■×100% i=1，2，…，n

计算■（0）（i）与原始序列X（0）（i）的关联度，当关联度大于0.6为满意。

最后进行后验差检验，计算原始序列标准差：S1=■

绝对误差序列的标准差：S2=■

方差比为：C=■

小误差概率为：P=P{Δ（0）（i）-■（0）<0.6745S1}

查找等级对照表，对GM（1，1）模型进行检验，若能通过则可以用模型进行预测，否则，进行残差修正。

四、EWMA控制图中的GM（1，1）模型

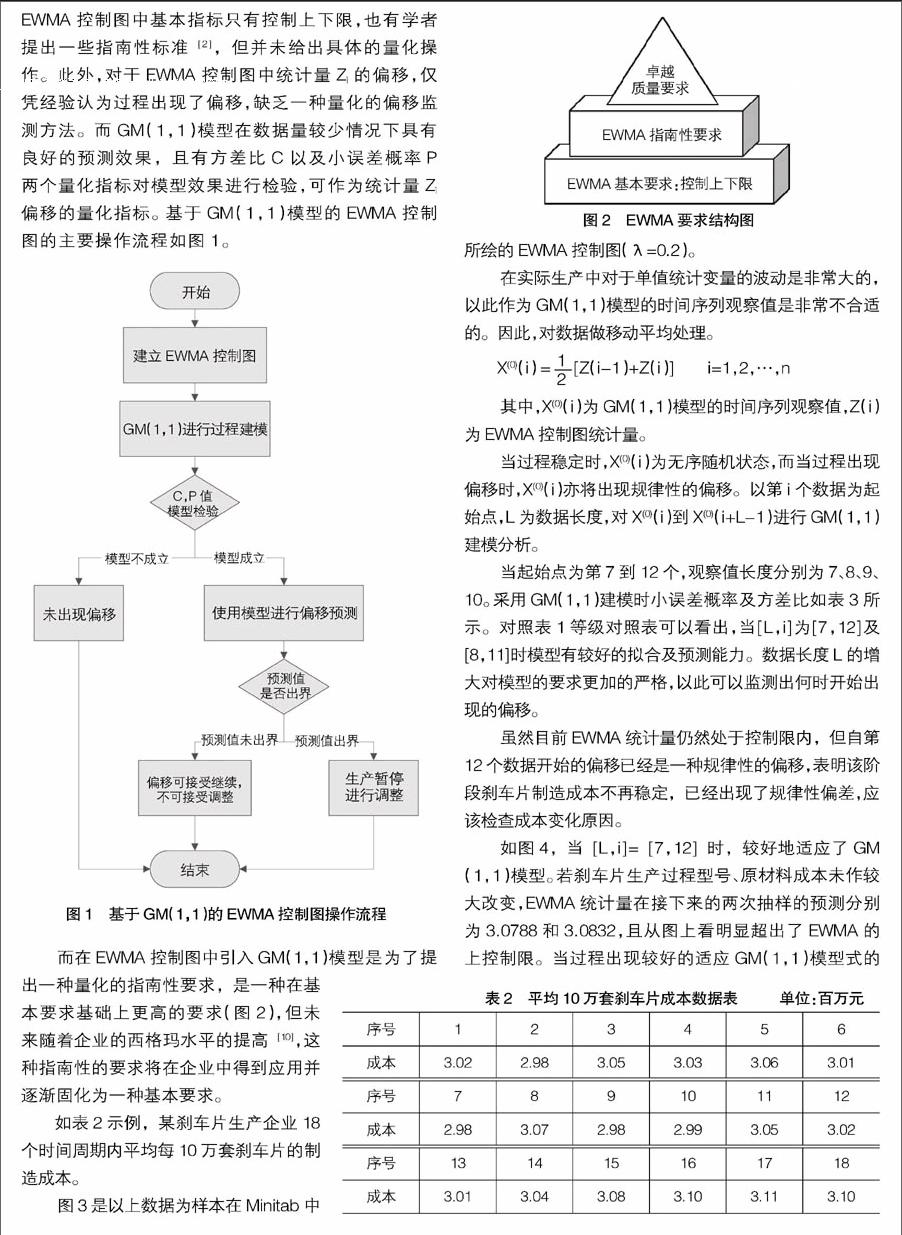
EWMA控制图在监测变异小于1.5σ时其灵敏度要大大高于传统的休哈特控制图[8]。不同于休哈特控制图中常用的8种检验方法[9]，EWMA控制图中基本指标只有控制上下限，也有学者提出一些指南性标准[2]，但并未给出具体的量化操作。此外，对于EWMA控制图中统计量Zi的偏移，仅凭经验认为过程出现了偏移，缺乏一种量化的偏移监测方法。而GM（1，1）模型在数据量较少情况下具有良好的预测效果，且有方差比C以及小误差概率P两个量化指标对模型效果进行检验，可作为统计量Zi偏移的量化指标。基于GM（1，1）模型的EWMA控制图的主要操作流程如图1。

而在EWMA控制图中引入GM（1，1）模型是为了提出一种量化的指南性要求，是一种在基本要求基础上更高的要求（图2），但未来随着企业的西格玛水平的提高[10]，这种指南性的要求将在企业中得到应用并逐渐固化为一种基本要求。

如表2示例，某刹车片生产企业18个时间周期内平均每10万套刹车片的制造成本。

图3是以上数据为样本在Minitab中所绘的EWMA控制图（λ=0.2）。

在实际生产中对于单值统计变量的波动是非常大的，以此作为GM（1，1）模型的时间序列观察值是非常不合适的。因此，对数据做移动平均处理。

X（0）（i）=■[Z（i-1）+Z（i）] i=1，2，…，n

其中，X（0）（i）为GM（1，1）模型的时间序列观察值，Z（i）为EWMA控制图统计量。

当过程稳定时，X（0）（i）为无序随机状态，而当过程出现偏移时，X（0）（i）亦将出现规律性的偏移。以第i个数据为起始点，L为数据长度，对X（0）（i）到X（0）（i+L-1）进行GM（1，1）建模分析。

当起始点为第7到12个，观察值长度分别为7、8、9、10。采用GM（1，1）建模时小误差概率及方差比如表3所示。对照表1等级对照表可以看出，当[L，i]为[7，12]及[8，11]时模型有较好的拟合及预测能力。数据长度L的增大对模型的要求更加的严格，以此可以监测出何时开始出现的偏移。

虽然目前EWMA统计量仍然处于控制限内，但自第12个数据开始的偏移已经是一种规律性的偏移，表明该阶段刹车片制造成本不再稳定，已经出现了规律性偏差，应该检查成本变化原因。

如图4，当[L，i]=[7，12]时，较好地适应了GM（1，1）模型。若刹车片生产过程型号、原材料成本未作较大改变，EWMA统计量在接下来的两次抽样的预测分别为3.0788和3.0832，且从图上看明显超出了EWMA的上控制限。当过程出现较好的适应GM（1，1）模型式的偏移，且使用模型预测未来变化尚未超出EWMA上下控制限时，若清查偏移原因成本较大，对于小批量产品可以不进行处理；而若明显超出控制限，则应及早查清制造成本增长原因，减少损失。

五、结语

本文提出了一种基于灰色的EWMA控制图，采用GM（1，1）对控制过程建模，确定制造成本是否出现偏移。利用模型对制造成本偏移过程进行预测，结合上下控制限提出指南性的EWMA控制图异常判定方式。处在可接受范围内的制造成本偏移将持续关注；而对于在预测模型中成本出界的警报应立即查找异常，及早减少损失。

【参考文献】

[1] 常志远，孙金生.变采样间隔自适应EWMAt控制图统计设计[J].计算机集成制造系统，2015（11）：2937-2944.

[2] ROBERTS S W. Control chart tests based on geometric moving averages[J].Technometrics，2000，42（1）：239-250.

[3] 孙静. 接近零不合格过程的有效控制：实现六西格玛质量的途径[M].北京：清华大学出版社，2005：157-165.

[4] WOODALL W H，MAHMOUD M A.The Inertial Properties of Quality Control Charts[J].Technometrics，2005，47（4）：425-436.

[5] 邓聚龙.灰色系统基本方法[M].武汉：华中工学院出版社， 1987.

[6] JOU J M， CHEN P Y， SUN J M. The gray prediction search algorithm for block motion estimation[J]. IEEE Transactions on Circuits & Systems for Video Technology， 1999， 9（6）：843-848.

[7] 黃克.灰色预测模型算法的改进研究[J].系统科学与数学，2015，35（11）：1347-1357.

[8] 何曙光，何桢，齐二石.基于马尔可夫链模型的EWMA控制图性能分析与优化[J].系统工程与电子技术，2008，30（6）：1127-1130.

[9] NELSON L S. The Shewhart Control Chart-Tests for Special Causes[J]. Journal of Quality Technology，1984，16（4）：237-239.

[10] 李晓晟. 精益生产、六西格玛和ERP的结合研究[J]. 中国管理信息化，2012，15（1）：36-38.