“百分数的意义”教学案例
徐志敏
“百分数的意义”是人教版六年级上册第六单元的内容,是学生学习百分数与分数、小数互化和用百分数知识解决问题的基础。要正确理解百分数的本质,重要的是体会百分数与除法、分数、倍、比之间的联系。教学时,我紧紧围绕“关系”一词,着眼于百分数与分数、比、倍之间的联系,从百分数表示部分与整体关系和两个独立量的关系两方面完整建构百分数的概念,凸显百分数的内涵。
【教学过程】
一、课前交流,渗透“关系”。
1.比体重
师:同学们,上课之前我们一起开动脑筋比比看,(出示课件)哪个胖一些,哪个瘦一些?思考问题真全面,要把身高和体重结合起来才能比出谁胖谁瘦。
2.投篮比赛
师:(出示表格)谁的投篮水平高?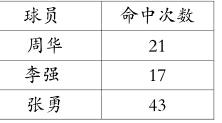
部分学生立即判断出张勇的投篮水平高,理由是张勇投中的球最多。
师:有没有不同意见?
生1:我认为不一定是张勇,如果他们三个投的总数不一样呢?
师:能举个例子说明吗?
生1:比如李强投了17次,那就是百发百中。
师:你的意思是这里需要把投中个数和投篮总数两个数量结合起来才能比较,是吗?如果知道了他们的投中个数和投篮总数,怎么结合就能判断出谁的水平高呢?那我们就一起解决这个问题。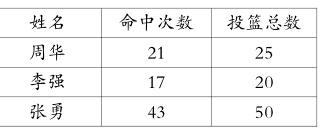
设计意图:课始紧紧围绕“关系”一词引发学生思考:进行比较是有前提的,只考虑单一要素不能得出正确的结果。
二、创设情境,感受百分数的产生和价值。
1.独立研究,小组交流
师:数学中,两个量结合就是将两个量进行一种运算,是加还是减?抑或是乘、除?下面请大家先独立思考,然后以小组为单位进行交流。
2.经历过程,感受百分数的优势
师:老师巡视了一圈,发现大家用了减法或除法将投中个数和投篮总数进行了结合。我们一起看一看。(用减法求出投不中的次数再比较)用减法求出了什么?哪些同学也是用了作差的方法,这种方法怎么样?为什么?
生2:投篮总数一样多的话可以运用,总数不一样则不适用。
师:我也投过篮,我投了一次,结果没进,我失误的次数是1-0=1(次)。那我是不是比他们都厉害?看来用减法比较他们的成绩不太科学。
师:(用除法将投中个数和投篮总数进行结合)用除法将两个量组合成分率,这几个分率表示的是什么?刚才每个人的投中个数和投篮总数还是两个数,这么一组合,它们还是表示具体的数量吗?变成了(关系),太了不起了。现在比较一下,谁的投篮水平高?用这两个量的关系去比,不能一眼就看出来,谁有什么好办法?
生3:把这三个分数的分母都化成100,就很容易比较它们的大小。
师:现在能一眼看出谁的投篮水平高吗?大家感觉这种方法怎么样?(简便)为什么?(便于比较)
师:同学们,像这些分母是100的分数,我们还有另外一种表示方法(课件依次出现:86%、85%、84%),这样的数就是我们今天要学习的百分数。(板书课题:百分数)现在老师有一个问题,既然分数能表示投中个数与投篮总数之间的关系,为什么还要发明百分数呢?
3.百分数的读写法
师:这几个百分数,有谁会读吗?(学生一起读:百分之八十四、百分之八十五、百分之八十六)看来会读的同学是全班同学的100%。百分数大家会读了,那会写吗?有谁愿意上台示范一下?
学生写,教师根据学生写的顺序板书:先寫分子85,再写%,这个符号叫做百分号。
师:这个同学写得又规范又漂亮,掌声送给他。你们想不想写一写,请同学们把这几个百分数在本子写一写。
设计意图:学生通过情境给出的一组信息判断谁的投篮水平高,初步建构百分数的意义。
三、探索感悟,建构百分数意义。
1.生活中的百分数
师:我们认识了百分数,想一想,在生活中你见过百分数吗?说一说。
2.理解百分数概念:整体和部分的意义
师:瞧,老师带来了一瓶农夫果园饮料,这里面就有百分数。在哪呢?看看。
生4:30%。
师:这里的30%表示谁是谁的30%?如果用这个正方形表示饮料的总量,要准确地在这个正方形中表示果蔬含量是饮料总量的30%,该怎么办?是这样吗?(从图上可以看出红色的部分是这个正方形的30%)
师:生活中很多人喜欢喝纯度更高的果蔬饮料,如果这瓶饮料中果蔬的含量再高一些,可能是百分之几?当果蔬含量是饮料总量的100%时,这个饮料就变成了什么?(纯果蔬汁)哇,想象一下一定很好喝。为了更好喝一点,能不能让果蔬的含量超过100%?为什么?
生5:我认为可以,因为果蔬可以不断提纯嘛,最终可以超过100%。
生6:我不同意,如果果蔬的含量超过100%,就超过了饮料总量,就装不下了!
师(故意调侃):你的意思是瓶子小,装不下了,那可以换个大瓶子嘛!(众生笑)
生7:老师,不是装下装不下的问题,果蔬本身就是饮料总量的一部分,再多也不可能超过饮料总量啊!
师:他说得怎么样?(教室里响起了热烈的掌声)饮料带来了是要喝的,老师把这瓶饮料摇匀,倒到杯子里,思考:现在杯中饮料的果蔬含量是多少?(30%)(继续倒入饮料)现在呢?(30%)(再倒一点)那现在呢?
生:还是30%。
师:明明我倒了这么多饮料,你们为什么说果蔬含量还是30%呢?
生8:因为30%表示果蔬与整杯饮料的一种关系。
师:你说得太棒了!也就是说,这里的30%并不能表示具体数量,而是表示果蔬与整杯饮料间的一种分率关系。所以我们又把百分数叫做百分率。
设计意图:借助实物引导学生理解百分数的意义,理解部分与整体的关系时,百分数不能超过百分之百。
3.理解百分数概念:表示两个独立数量的关系
师:一瓶农夫果园饮料让我们对百分数有了更深刻的认识。接着请看(出示图):说说甲车的速度是乙车的百分之几?你是怎么想的?
生9:甲车速度是乙车速度的80%。乙车速度是单位“1”,将甲车速度和乙车速度进行比较。
师:你真棒!如果这里乙车的速度不变,甲车的速度逐渐加快,那么甲车的速度可能是乙车的百分之几?
生10:甲车的速度可能是乙车的百分之百,说明甲车速度和乙车速度相等。
师:如果甲车的速度继续加快,甲车的速度是乙车速度的百分之几?
生10:110%。
师:甲车的速度可以是乙车的110%吗?
生:可以呀!
师:刚才我们研究果蔬含量的问题,为什么饮料中果蔬的含量最多只能是100%,而比较甲车的速度是乙车的百分之几时,可以是110%?
生11:因为果蔬含量是饮料总量的一部分,再多也就是和总量一样多。而甲车的速度和乙车速度比较,乙车速度是一个参照,甲车的速度可以超过它。
师:他讲乙车速度是两个数比较时的一个参照,也就是作比较的一个标准,非常好!甲车的速度是乙车的105%,说明甲车速度比乙车速度快。甲车的速度是乙车的110%,也可以说甲车的速度是乙车的1.1倍,这和我们以前学过的倍数关系是一样的,只是表示的形式发生了变化。
设计意图:通过生活实例,学生感悟百分数表示两个独立数量的关系时,这个百分数可以小于100%,也可以等于100%、大于100%,從而全面感悟百分数的意义。
4.归纳百分数概念,沟通联系
师:我们把刚才认识的百分数整理整理,这几个百分数还可以用我们学过的什么数表示呢?
师:是啊,以前我们将两个数进行比较时,如果一个数比另一个小,通常用几分之几表示;如果一个数比另一个数大,通常用几倍表示。学了百分数以后,不管哪种情况都可以用百分数表示。通过学习,你对百分数有了哪些新的认识呢?
生12:我觉得百分数表示两个数进行比较。(适时揭示:百分数也叫百分比)
生13:我知道百分数跟分数一样,都有单位“1”的量,有另一个量跟它比较。
师:说得好!百分数表示的是一个数是另一个数的百分之几,它跟一个数是另一个数的几分之几或几倍在本质上是相同的。
设计意图:引导学生将一个数是另一个数的百分之几纳入到已有认知结构中,自主建构数学知识网络。
四、应用巩固,理解分数与百分数的联系及区别。
师:请根据你的理解,选择合适的数填在括号里。(学生先独立思考,然后小组交流)
(课件出示)
1.地球上海洋的面积大约占地球表面积的()。
2.一条绳子长约()米。
3.我国的土地面积正在以每年()的速度被沙漠侵吞。
五、拓展引申,升华认识
师:学到这,百分数的知识你们都学懂了吗?对于百分数你还有什么问题吗?其实老师也有一个问题,既然有百分数,那会不会有十分数、千分数、万分数呢?你们认为会有吗?好,我们一起看看老师的研究(观看微课:千分数、打折、PPM(百万分数))。交给你们一个任务,放学后请上网查一查这些数在什么情况下使用。
设计意图:借由学生的疑问,引导学生既关注百分数的意义,更关注百分数的现实价值,拓宽知识面。
(作者单位:株洲市北星小学)

