槽式太阳能有机朗肯循环发电系统的模拟研究

安玉磊， 陈九法， 章智博

(1. 东南大学 能源与环境学院， 南京 210096； 2. 浙江省建筑设计研究院， 杭州 310006)



槽式太阳能有机朗肯循环发电系统的模拟研究

安玉磊1， 陈九法1， 章智博2

(1. 东南大学 能源与环境学院， 南京 210096； 2. 浙江省建筑设计研究院， 杭州 310006)

把槽式太阳能集热器与有机朗肯循环系统相结合，模拟槽式太阳能集热器的相关参数对发电系统的影响。建立了槽式太阳能有机朗肯循环系统的数学模型和系统各部件的计算模型，采用VB软件对循环系统整体进行模拟。分析了系统整体效率和膨胀机输出功受太阳直射辐射强度、导热流体入口流体温升和入口速度的影响。模拟发现，当集热器入口和出口温度固定时，系统存在最佳流速，最佳流速与太阳直射辐射强度和入口温度都有关。

槽式太阳能发电； 有机朗肯循环； 数值模拟

根据国际能源署统计数据，2007 年中国已成为全球第一大CO2排放国[1]，面对碳排放对大气的污染，我国制定了到2030年必须达到单位国内生产总值CO2排放比2005年下降60%～65%的目标。降低碳排放，太阳能是首选。我国的太阳能资源非常丰富，全国大概有三分之二以上地区的年太阳辐射量超过5 000 MJ/m2，太阳能的利用对减少碳排放有重要意义。目前太阳能光电研究已有很大进展，但光电效率只有15%左右，且连续性较差，世界上对太阳能的研究主要集中在光热转化。

槽式太阳能热发电系统利用多个槽式聚光器将太阳光反射到位于镜面焦点处的集热管，对集热管内部的传热工质进行加热，产生高温高压蒸汽，推动汽轮机进行发电。传统的化石燃料用在热发电上比较成功，但是，汽轮机的发电占地面积大、要求较高的工质参数和大机组容量，最小也要达到6～7 MW，不适用于中低温发电。有机朗肯循环(ORC)系统运用有机工质驱动膨胀机进行发电，在利用中低温太阳能上，具有独特的优势。乔卫来等[2]利用RKS模型，分析了19种有机工质的动力循环参数发现工质，并结合GWP和ODP环境指标，发现R142b、Rc318与R600适合于低温朗肯循环。

笔者针对ORC系统，结合槽式太阳能集热器的光学与热力学性能，通过VB语言编写程序，实现槽式太阳能ORC相关参数的计算，分析了在太阳能转化成电能的过程中各因素对效率和功率的影响。

1 系统描述

图1是该发电系统的结构图，图中热源部分管道里流的是导热油；ORC发电部分管道里流的是有机工质；冷凝部分管道里流的是冷却水。

图1 槽式太阳能ORC发电系统结构图

2 系统数学模型

2.1 ORC热力计算

ORC的温熵图见图2。

1—工质蒸发器出口的过热状态点；2—高温高压蒸汽工质经过膨胀机膨胀做功后的状态点；3—从膨胀机排出的工质经过冷凝器冷凝后的状态点；4—工质泵加压后工质的状态点；5—预热器中

经过预热的工质状态点。

图2 ORCT-s图

2.1.1 有机工质在预热器和蒸发器中的热力过程4-1

在预热器中有机工质吸收热量为：

Q4-5=qmref(h5-h4)=qmr·cp(tb-tc)

(1)

蒸发器中吸收热量为：

Q5-1=qmref(h1-h5)=qmr·cp(ta-tb)

(2)式中：qmref为有机工质质量流量，kg/s；qmr为热流体质量流量，kg/s；cp为热流体平均比定压热容，kJ/(kg·K)；ta为热流体蒸发器进口温度，℃；tb为热流体蒸发器出口温度，℃；tc为热流体预热器出口温度，℃。

在蒸发换热器中，有机工质与热流体传热之间存在一个窄点温差Δtzd，取3～7 K[3]，本设计取5 K。根据有机工质与热流体在蒸发器和预热器中的热交换过程可知，蒸发器出口流体的温度tb可以表示为tb=Te+Δtzd，所以由式(2)可得工质流量公式为：

qmref=cp·qmr(ta-Te-Δtzd)/(h1-h4)

(3)

式中：Te为蒸发温度，℃。

2.1.2 有机工质在冷凝器中的热力过程2-3

在冷凝器中工质放出的热量可以表示为：

Q2-3=qmref(h2-h3)=qmwat·cpwat(te-td)

(4)式中：cpwat为冷却水平均比定压热容，kJ/(kg·K)；qmwat为冷却水质量流量，kg/s；td为冷却水入口温度，℃；te为冷却水出口温度，℃。

在冷凝器中工质冷凝温度通常比冷却水出口温度要高3～7 K，冷却水的温升Δtde=te-td，通常取5～8 K[3]。冷却水流量公式为：

qmwat=qmr(h2-h3)/(cpwat·(te-td))

(5)

2.1.3 有机工质在膨胀机中做功的热力过程1-2

假设有机工质在膨胀机中的膨胀过程处于稳态，则膨胀机的等熵膨胀效率可以表示为：

ηT=(h1-h2)/(h1-h2s)

(6)

膨胀过程中，工质所做的功可以表示为：

W1-2=qmref(h1-h2)

(7)

2.1.4 ORC净输出功及效率

在实际的发电过程中，系统对外输出功的同时，系统也产生功耗，计算系统的系统效率和净输出功时，必须先减去系统本身的功耗。工质泵、冷却水泵以及导热油泵的功耗计算采用以下公式：

Wrp=qmref·V3(p4-p3)/ηp

(8)

Wp1=qmwat·gH1/ηp1

(9)

Wp2=qmr·gH2/ηp2

(10)

式中：ηp为工质泵的工作效率；V3为工质在状态3点的比体积，m3/kg；ηp1为冷却水泵的工作效率；ηp2为导热油泵的工作效率；H1、H2分别为工质泵扬程和冷却水泵扬程，m。

因此，ORC系统的净输出功可以表示为：

Wnet=W1-2-Wrp-Wp1-Wp2

(11)

工质从热源获得的总热量为Q1-4，则系统的循环效率为：

(12)

综合集热器的效率，整体的系统循环效率为：

(13)

式中：Ibh为地表水平面上的直射辐射强度，W/m2；Ar为集热器反射镜采光面积，m2。

2.2 系统各部件计算模型

2.2.1 蒸发器传热计算模型

选择目前高压较常使用的板式换热器作为ORC系统的蒸发器。

采用参考文献[4]关于蒸发器换热模型的假设。

(1) 蒸发器基本传热方程。

Qe=Ke·Ae·ΔTe,m

(14)

式中：Qe为蒸发传热量，W；Ae为蒸发器换热面积，m2；Ke为蒸发器综合传热系数，W/(m2·K)；ΔTe,m为对数平均温差，K。

(2) 蒸发器的综合传热系数。

(15)式中：αei为有机工质侧对流传热系数，W/(m2·K)；αw为热流体侧对流传热系数， W/(m2·K)；R1、R2为板片两侧污垢热阻，(m2·K) /W；σp为板片厚度，m；λp为板片导热系数，W/(m·K)。

(3)导热油侧对流传热系数计算。

导热油侧为单相流动换热，传热系数较大，笔者采用Yan YY关联式[5]进行计算：

(16)

(17)

(4)有机工质侧对流传热系数计算。

两相区有机工质对流传热系数计算采用下式：

(18)

2.2.2 冷凝器传热计算模型

冷凝端不需要承受高温高压，因此冷凝器采用套管式换热器。

(1) 冷凝器基本传热方程。

Qc=Kc·Ac·ΔTc,m

(19)

式中：Qc为冷凝器换热量，W；Ac为冷凝器换热面积，m2；Kc为冷凝器综合传热系数，W/(m2·K)；ΔTc,m为对数平均温差，K。

(2) 套管式冷凝器的综合传热系数。

(20)

(3) 管外冷却水的对流传热系数。

(21)

(4) 管内有机工质对流传热系数计算。

管内有机工质对流换热按照单相区和两相区分别进行计算。

单相换热时，按照Re的不同选择相应的公式，管内Re定义为：

(22)

当Re≤2 300时，管内流动状态为层流，管内传热系数可按下式进行计算[6]：

(23)

式中：λw为管内有机工质的导热系数，W/(m·K)。

当2 300≤Re≤104时，管内流动状态为过渡流，使用V.Gnielinski[7]整理相关的实验数据得到的经验关联式，计算管内流体传热系数：

对于气体

αw=0.021 4(Re0.8-100)Pr0.4

(24)

对于液体

αw=0.012(Re0.87-280)Pr0.4

(25)

式中：l为管长，m；Pr为普朗特数；Prwall为壁温计算下的普朗特数；T为流体温度，℃；Twall为壁面温度，℃。

当Re≥104时，流动状态为湍流，使用Dittus-Boelter公式[6]计算管内流体的传热系数：

(26)

相变传热时，管内有机工质对流传热系数采用Gungor和Winterton提出的经验关联式进行计算[7]。

2.2.3 膨胀机和工质泵模型

为了简化计算考虑膨胀机和工质泵的等熵效率取定值，根据相关参考文献，选定膨胀机的总效率为75%，工质泵的等熵效率为70%。

2.3 槽式太阳能集热器热力计算

槽式太阳能集热器的主要能量传递和热损失过程见图3。

Q0—集热管接收的太阳辐射能；Q12—传热流体工质吸收的热量；Q23—通过集热管金属吸热管壁面的热量；Q34—金属吸热管外壁面与玻璃套管内壁面之间的换热量；Q45—通过玻璃套管的导热量；Q56—玻璃套管外壁面与环境空气之间的对流换热量；Q57—玻璃套管外壁面与天空之间的辐射换热量。

图3 槽式太阳能集热器能量传递过程示意图

根据能量守恒定律可以得到图3中真空集热管的能量平衡关系式。

真空集热管接收到的太阳辐射为：

Q0=IbhArηopt(1-εgo)

(27)

式中：Ar为集热器抛物面反射镜采光面积，Ar=W·LSCA， m2；ηopt为光学效率；εgo为玻璃管外表面发射率。

传热流体工质得到的热量：

Q12=qmrcp(Tout-Tin)

(28)

式中：cp为传热流体工质的比定压热容， J/(kg·K)；qmr为传热流体工质的质量流量，kg/s；Tout为集热管传热工质的出口温度，K；Tin为集热管传热工质的进口温度，K。

集热管总体热量损失：

Qloss=Q56+Q57

(29)

集热管的总体能量平衡方程为：

Q0=Q12+Qloss

(30)

在金属管内壁侧，能量主要通过对流的形式传递给传热工质，存在能量平衡方程：

Q12=Q23

(31)

在金属管外壁侧，集热管吸收的太阳辐射一部分通过金属管壁面导热传给传热流体工质，另一部分通过对流、辐射和导热(金属管与玻璃管之间并不完全真空，存在残余气体引起的导热)的形式传递给玻璃套管，存在能量平衡方程：

Q0=Q23+Q34

(32)

其中，Q34可以表示为：

Q34=Q34conv+Q34rad+Q34cond

式中：Q34conv为金属吸热管外壁面与玻璃套管内壁面之间的对流换热量，W；Q34rad为辐射换热量，W；Q34cond为导热换热量，W。

在玻璃套管内壁面侧，金属吸热管传递到玻璃套管内壁面侧的能量以导热的形式传递到玻璃套管外壁面，因此，存在能量平衡方程：

Q34=Q45

(33)

在玻璃管外壁面侧，通过导热传递出来的能量会以对流和辐射换热的形式，散失到周围环境中，这部分能量也就是集热管的热损失，存在能量平衡方程：

Q45=Q56+Q57

(34)

槽式太阳能集热器的集热效率定义为：

(35)

笔者结合实际需求选用R113作为ORC工质。R113的临界温度为214.1 ℃，临界压力为3.39 MPa，具体参数见表1。

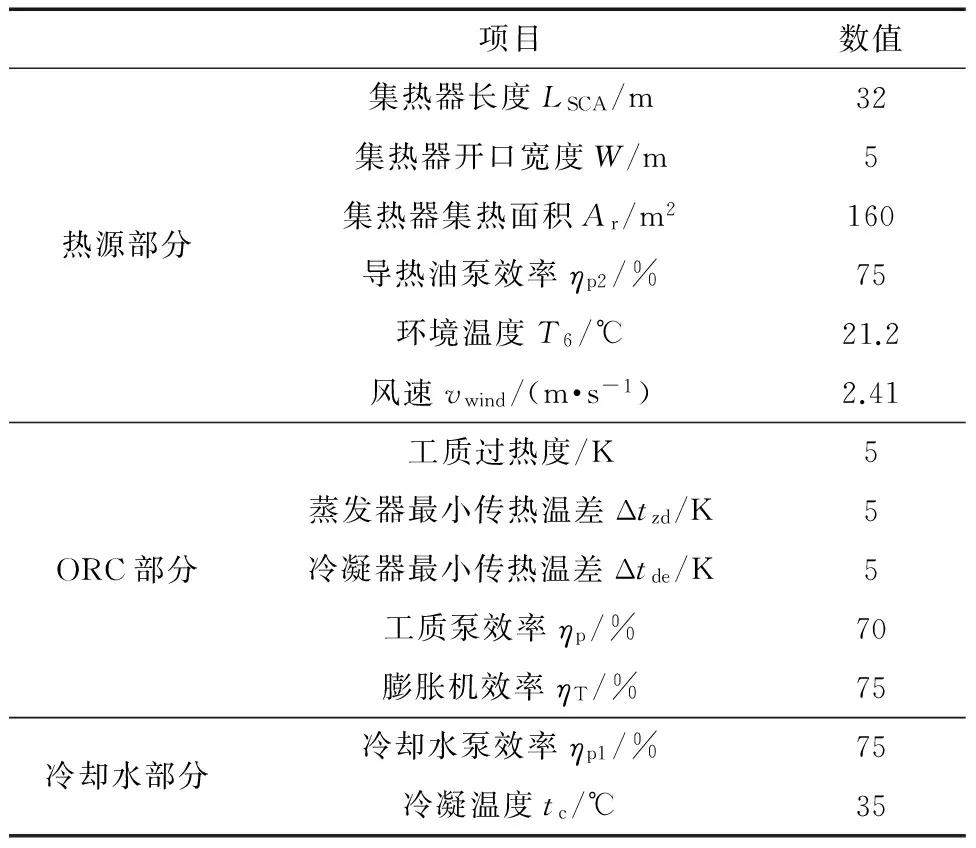
表1 槽式太阳能ORC参数设定

模型建立后，通过RKS方程，运用VB软件计算循环工质的焓、熵、压力等参数，并与物性查询通用软件Refprop所得值进行比较，得出相对误差在4%以内，相对误差焓、熵等都在精度范围内，数据比较准确，对于工程应用具有指导价值。

3 系统计算结果与性能分析

3.1 太阳辐射强度对系统效率的影响

模拟条件取集热管导热油进口流速为1 m/s，其他模拟条件见表2。

图4为槽式太阳能集热器导热油入口温度分别为100 ℃和150 ℃时，太阳能ORC系统整体效率随太阳直射辐射强度的变化。在导热油入口参数一定的情况下，系统整体效率随着太阳直射辐射强度的增加而增大。一方面是因为太阳直射辐射强度的增加，导致集热器内传热流体温升增大，在入口温度一定的情况下，ORC系统的蒸发温度升高，系统效率增大；另一方面是因为随着太阳直射辐射强度的增加，槽式太阳能集热器集热效率增大。

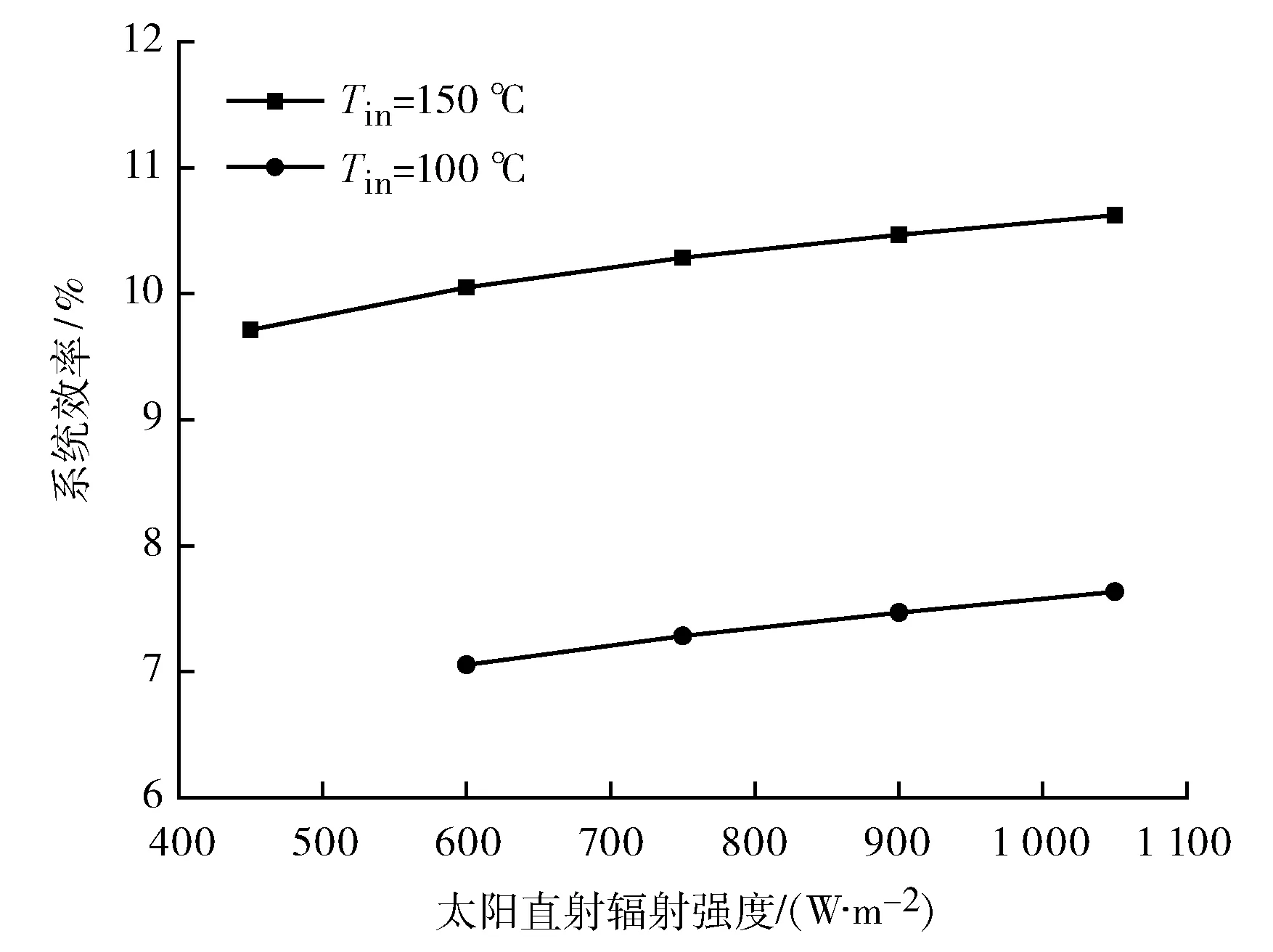
图4 系统效率随太阳直射辐射强度的变化

图5为槽式太阳能集热器导热油入口温度分别为100 ℃和150 ℃时，太阳能ORC系统膨胀机输出功随太阳直射辐射强度的变化。

图5 系统膨胀机输出功随太阳直射辐射强度的变化

在导热油进口参数一定的情况下，膨胀机输出功随着太阳直射辐射强度的增加而增加，膨胀机输出功增加的幅度大于系统整体效率，并且导热油入口温度高时，会有更大的增加幅度。分析其原因，主要是系统整体效率随着太阳直射辐射强度的增加而增大。

3.2 集热器流体入口温度对系统效率的影响

模拟条件取集热管导热油入口速度为1 m/s，太阳直射辐射强度为900 W/m2，其他模拟条件见表2。

图6为不同导热油入口温度条件下，太阳能ORC系统整体效率随导热油入口温度的变化。

图6 系统效率随集热器进口导热油温度的变化

在环境参数和集热器导热油入口速度一定的情况下，随着进口温度的升高，系统整体效率随之增大，但是增幅逐渐降低。原因是随着导热油进口温度的升高，ORC系统对应的蒸发温度逐渐升高，ORC系统效率显著升高，由于集热器的集热效率下降，系统整体效率虽然随进口温度升高而增大，但是增幅逐渐减小。

图7为不同导热油进口温度条件下，太阳能ORC系统膨胀机输出功随导热油进口温度的变化。

图7 系统膨胀机输出功随集热器进口导热油温度的变化

在环境参数和集热器导热油入口速度一定的情况下，膨胀机输出功随导热油进口温度的升高而增加，增加曲线类似于整体效率增加的曲线。原因是在环境参数相同、集热器导热油入口速度一定的情况下，ORC系统吸热的热量相差不多。

3.3 集热器流体入口速度对系统效率的影响

模拟条件取集热器导热油入口温度分别为150 ℃和100 ℃，太阳直射辐射强度为900 W/m2，其他模拟条件见表2。

图8为导热油入口温度分别为100 ℃和150 ℃时，太阳能ORC系统整体效率随导热油进口速度的变化。

图8 系统效率随集热器入口速度的变化

图9为导热油入口温度分别为100 ℃和150 ℃时，太阳能ORC系统膨胀机输出功随导热油入口速度的变化。

图9 系统膨胀机输出功随集热器入口导热油温度的变化

从图8和图9中可以看出：随着集热器入口导热油流速的增加，太阳能ORC膨胀机输出功减少，系统整体循环效率降低。原因是模拟假定条件是集热器导热油的入口温度为100 ℃或150 ℃的定值，随着导热油流速的增大，集热器的出口温度降低，从而导致ORC系统的蒸发温度降低，系统效率降低。

由于集热器长度的限制，在有机工质不超过临界温度的情况下，集热器导热油流速越低，出口温度越高，则系统效率越高。

图10为太阳能ORC系统在集热器入口和出口导热油温度一定的情况下，系统整体效率随导热油进口速度的变化。假设入口和出口温差为50 K。

图10 集热器入口和出口温度相同条件下系统效率随集热器进口速度的变化

当导热油入口和出口温差一定时，系统整体效率存在一个最大值，并不随导热油入口速度的增大而单调减小。原因是当导热油入口和出口温差恒定时，ORC系统的蒸发温度相差不大，系统整体效率主要受集热器效率和导热油泵功耗的影响。集热器集热效率随着流体入口速度增加而增加，同时，集热器管道压损增加，导热油泵功耗增加。由图10可见：太阳直射辐射强度为450 W/m2、Tin=100 ℃时，集热器流体进口的最佳流速在1 m/s左右；太阳直射辐射强度为900 W/m2、Tin=100 ℃时，最佳流速在1～1.2 m/s；太阳直射辐射强度为450 W/m2、Tin=150 ℃时，最佳流速也在1～1.2 m/s；太阳直射辐射强度为900 W/m2、Tin=150 ℃时，最佳流速在1.2～1.4 m/s。主要是因为，随着太阳直射辐射强度的增大，集热器流体入口温度的升高，传热流体黏度减小，管道压损减小，所以集热器的最佳流速增大。

4 结语

通过模拟分析太阳直射辐射强度、入口流体温度和入口流体速度对太阳能ORC系统的影响。主要得出如下结论：

(1) 太阳能ORC系统整体效率随太阳直射辐射强度的增加而增大，膨胀机输出功同样随太阳直射辐射强度的增加而增加，并且增幅更大。

(2) 太阳能ORC系统的整体效率和膨胀机输出功都随集热器入口流体温度的升高而增大，增幅逐步降低。

(3) 随着集热器入口流体速度的减小，整体循环系统的效率减小，膨胀机输出功同样减小，但是减小的幅度要小于系统整体效率的减小幅度。

(4) 当集热器入口和出口温度固定时，存在最佳流速，使整体循环系统的效率最大。最佳流速与集热管内传热流体的进口温度以及太阳直射辐射强度的大小都有关。当系统工况从太阳直射辐射强度为450 W/m2、Tin=100 ℃变化到太阳直射辐射强度为900 W/m2、Tin=150 ℃工况时，最佳流速从1 m/s变化到1.2～1.4 m/s。

[1] 程叶青,王哲野,张守志,等. 中国能源消费碳排放强度及其影响因素的空间计量[J]. 地理学报,2013,68(10): 1418-1431.

[2] 乔卫来,陈九法,薛琴,等. 太阳能驱动有机朗肯循环的工质比较[J]. 能源研究与利用,2010(2): 31-36.

[3] 严家 . 低温热能发电方案中选择工质和确定参数的热力学原则和计算式[J]. 工程热物理学报,1982,3(1): 1-7.

[4] CHEN J C. Correlation for boiling heat transfer to saturated fluids in convective flow[J]. Industrial & Engineering Chemistry Process Design and Development,1966,5(3): 322-329.

[5] 景步云,谷波,黎远光. 板式蒸发器仿真计算模型[J]. 系统仿真学报,2003,15(10): 1481-1483.

[6] 杨世铭,陶文栓. 传热学[M]. 4版. 北京: 高等教育出版社,2006.

[7] COOPER M G. Saturation nucleate pool boiling: a simple correlation[C]//1st UK National Conference on Heat Transfer: The Institution of Chemical Engineers Symposium Series. Amsterdam: Elsevier,1984: 785-793.

声明

为适应我国信息化建设，扩大本刊及作者知识信息交流渠道，本刊已被《中文科技期刊数据库(全文版)》、《中国核心期刊(遴选)数据库》、《中国学术期刊网络出版总库》及CNKI系列数据库收录，有关作者文章著作权使用费与本刊稿酬一次性给付。如作者不同意文章被收录，请在来稿时向本刊声明，本刊将做适当处理。

Simulation Research on Trough Solar Organic Rankine Cycle Power Generation System

An Yulei1, Chen Jiufa1, Zhang Zhibo2

(1. School of Energy and Environment, Southeast University, Nanjing 210096, China;2. Zhejiang Prov. Institute of Architectural Design and Research, Hangzhou 310006, China)

By combining the trough solar collector with an organic Rankine cycle (ORC) system, the influence of collector parameters on the power generation system was simulated. A mathematical model for the trough solar ORC system and calculation models for various parts of the system were established to simulate the whole circulation system using VB software. The effects of direct solar radiation intensity, the inlet temperature rise and the inlet flow rate of heat transfer fluid on both the overall efficiency of system and the output power of expander were analyzed. Simulation results show that when the inlet and outlet temperature of collector are fixed, the system would have an optimal flow rate relating to both the direct solar radiation intensity and the inlet temperature.

trough solar power generation; organic Rankine cycle; numerical simulation

2016-05-11；

2016-06-04

安玉磊(1990—)，男，在读硕士研究生，研究方向为槽式太阳能发电和有机朗肯循环发电。

E-mail: an.yulei@139.com

TK513.3

A

1671-086X(2017)02-0092-07