钢筋石笼的空隙率对其稳定特性的影响

郭红民，张田甜，胡海松，胡文兵

(三峡大学 水利与环境学院，湖北 宜昌 443002)

钢筋石笼的空隙率对其稳定特性的影响

郭红民，张田甜，胡海松，胡文兵

(三峡大学 水利与环境学院，湖北 宜昌 443002)

钢筋石笼是截流、堵口和护岸工程中常用的一种人工材料，探索钢筋石笼的稳定性机理对指导其合理应用具有重要的意义。为研究空隙率对钢筋石笼稳定性的影响，针对不同形状及不同空隙率的钢筋石笼进行了起动试验，拟合提出了考虑其空隙率的钢筋石笼起动流速公式，对块体抗冲流速经典公式进行了补充和完善。研究表明：在其它影响因素相同的情况下，钢筋石笼的空隙率越大越稳定，且不同形状的钢筋石笼的稳定性有所不同。最终得到了包含大小、密度、形状、相对粗糙度等因子的钢筋石笼起动流速计算公式，经试验验证该公式具有较好的计算精度。

钢筋石笼；稳定性能；化引直径； 空隙率；起动流速；公式拟合

1 研究背景

钢筋石笼取材方便、制作容易，具有良好的稳定性、透水性和柔性，运输便捷，且方便抛投。因此，钢筋石笼在水利工程的截流和堵口施工中，无论经济性和安全性都具有巨大的优势，得到了广泛的关注和应用。

然而到目前为止，国内外有关钢筋石笼稳定性的研究成果并不多，使得钢筋石笼在工程应用中缺少相应的理论指导。特别是关于空隙率对钢筋石笼的稳定性的影响还没有前人对此做过准确量化的研究。基于此，本文对不同形状、不同空隙率的钢筋石笼进行了系列起动流速试验，探讨了不同空隙率对钢筋石笼稳定机理的影响，并拟合提出了考虑空隙率的钢筋石笼的起动流速公式。

2 研究现状及问题分析

起动流速的大小是衡量截流抛投材料稳定性好坏的一个综合性指标，传统经典的伊兹巴斯公式由于公式简单，需要的参数较少，一直被广泛应用于截流工程设计工作中，即

(1)

(2)

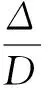
然而上述研究都没有涉及到钢筋石笼与其它材料最大的不同——透水性。考虑到前人对于空隙率对钢筋石笼稳定性的影响还没有做过准确量化的研究，本文把钢筋石笼的透水性和形状作为影响因素，通过一系列的起动流速试验，希望对以上实用公式作出一定的修正，对钢筋石笼的应用提供指导。

3 模型试验及分析

3.1 试验设计

钢筋石笼起动流速试验在长10 m，宽0.5 m，高0.75 m的玻璃水槽中进行。由于采用天然石料制作钢筋石笼较难形成相同的空隙率，为此，本试验采用大小均匀、个体质量精确的玻璃珠填充钢筋石笼，并按不同的形状、大小、空隙率制作了试验所需的钢筋石笼,试验所用钢筋笼形状如图1所示。

图1 不同形状的钢筋石笼Fig.1 Reinforced gabions of different shapes表1 试验所用钢筋石笼的特征尺寸Table 1 Characteristic sizes of reinforced gabions in the test

形状试验组钢筋笼编号边长/cm体积/cm3化引直径/cm质量/g空隙率n重度/(kN·m-3)A11778.240.4515.2①A128.05129.92824.320.4416.1 正六面体A13875.520.3917.1A21202.500.4416.2②A225.01256.20220.000.4117.6A23235.100.3518.8B11896.870.4417.5③B1216.35129.92952.320.4318.6 正四面体B13947.240.3718.5B21225.510.4518.0④B2210.21256.20256.250.4220.5B23257.870.3520.6C11ϕ上=4.3778.820.4415.2⑤C12ϕ下=10.85129.92812.930.4315.9 圆台型C13h=10.8859.370.3816.8C21ϕ上=2.7196.300.4615.7⑥C22ϕ下=6.81256.20201.250.4516.1C23h=6.8243.750.3819.5

注：φ上为圆台上底直径；φ下为圆台下底直径；h为圆台的高。

3.1.1 试验工况

本次试验分别研究了正六面体、正四面体、圆台型3种形状的钢筋石笼，每种形状的钢筋石笼共有2种不同尺寸大小，相同形状和尺寸的钢筋石笼分别配制了3种不同的空隙率，总计18组试验工况，试验钢筋石笼特征尺寸详见表1。

3.1.2 试验程序

选取水槽流速相对稳定的中间段作为试验段，为减小随机性所带来的影响，在试验段槽底上画出一条与水槽身垂直的标线，每次将钢筋笼放置在标线的同一位置进行起动流速试验。3种形状的钢筋石笼均在只发生滑动不发生倾倒和翻滚的情况下研究。本试验采用多普勒超声流速仪测量标线处截面的平均流速，截面取左中右3条垂线，垂线采用5点法，截面平均流速为这15点的平均值。通过伊兹巴斯公式算出试验钢筋石笼的综合稳定系数K，计算结果参见表2。

3.2 钢筋石笼的流速分布

各试验工况钢筋石笼开始起动时的垂线平均流速分布曲线如图2所示。同种形状大小的钢筋石笼，其流速分布曲线与空隙率的关系并没有呈现出明显的规律性，本文分析是由于未考虑到钢筋石笼重度的不同，需控制唯一变量为空隙率，在接下来的研究计算中进一步探讨空隙率与稳定性的关系。

3.3 试验钢筋石笼的综合稳定系数计算

试验结果表明，不同形状和大小的钢筋石笼的综合稳定系数随其空隙率的增大而增大的规律相似；形状相同的钢筋石笼，体积较大的，综合稳定系数也较大，如图3所示。

表2 钢筋石笼试验的稳定系数K计算结果Table 2 Results of stability factor K of reinforced gabions

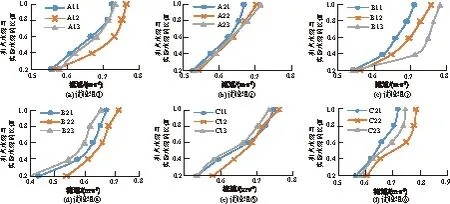
图2 钢筋石笼流速分布曲线Fig.2 Curves of the incipient velocity of reinforced gabions

图3 钢筋石笼空隙率对其稳定系数的影响Fig.3 Relation between stability factor and void ratio

4 钢筋石笼稳定计算公式拟合与验证

4.1 钢筋石笼的稳定计算公式拟合

为探究钢筋石笼空隙率与其起动流速的关系，在前述起动流速公式(2)的基础上，引入空隙率系数N，得到起动流速计算公式，即

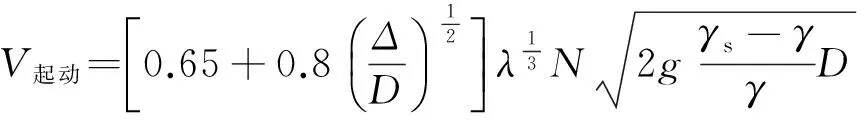
(3)

式中N是一个关于空隙率n的函数，N与n的关系可通过前述试验成果拟合得出。

由于本试验在光滑玻璃水槽中进行，查相关资料，其Δ=0.000 25～0.001 25 mm，本试验为正多面体，石笼形状不考虑扁度影响，λ取1；各试验工况相应V起动，Δ，D，γs，γ已知，根据式(3)计算可得N，将前面试验组①—⑥数据用MatLab进行拟合，得出3种形状的钢筋石笼空隙率n和空隙率系数N均成线性关系，见表3。

由试验资料可得，同形状钢筋石笼，虽大小不同、空隙率不同，但对空隙率系数N与空隙率n的比值影响很小；不同形状的钢筋石笼的空隙率系数N与空隙率n的比值有所不同；N与n基本成线性关系，即:正六面体钢筋石笼N=2n；正四面体钢筋石笼N=1.7n；圆台型钢筋石笼N=2.1n。

4.2 钢筋石笼的稳定计算公式的验证

为了验证式(3)的准确性，作者进一步进行了验证试验，针对以上3种形状分别制作新的尺寸及空隙率的钢筋石笼，正六面体为试验组⑦，正四面体为试验组⑧，圆台型为试验组⑨，在试验条件相同的情况下进行验证试验。将试验测得的钢筋石笼起动流速与依据式(3)计算所得的起动流速对比，对比结果见表4， 计算值与实测值的对比如图4所示。

表3 空隙率系数N与空隙率n的关系Table 3 Relationship between void ratio coefficient N and void ratio n

由表4和图4可知，本文拟合公式计算的起动流速值与试验实测的起动流速值基本吻合，误差较小，最大误差仅3.7%。

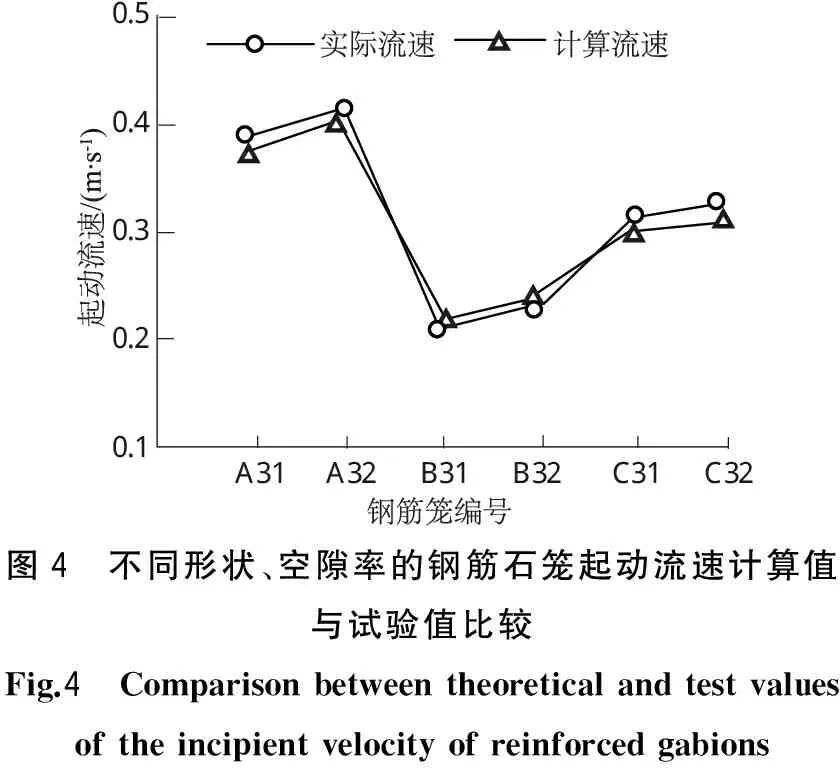
图4 不同形状、空隙率的钢筋石笼起动流速计算值与试验值比较Fig.4 Comparisonbetweentheoreticalandtestvaluesoftheincipientvelocityofreinforcedgabions

表4 钢筋石笼起动流速验证试验计算结果Table 4 Verification result of the incipient velocity of reinforced gabions

5 结 论

在总结前人研究的基础上，本文分析了钢筋石笼的稳定特性，通过试验研究，得到以下结论。

(1) 不同形状和大小的钢筋石笼的综合稳定系数随其空隙率的增大而增大的规律相似；形状相同的钢筋石笼，体积较大的，综合稳定系数也较大。

(2) 本文引入空隙率系数N,N是与空隙率n相关的函数。得出结论：同形状钢筋石笼，虽大小不同、空隙率不同，但对空隙率系数N与空隙率n的比值影响很小；不同形状的钢筋石笼的空隙率系数N与空隙率n的比值有所不同；N与n基本成线性关系。

(3) 本文拟合了钢筋石笼在考虑空隙率的情况下，包含大小、密度、形状、相对粗糙度等因子的钢筋石笼起动流速计算公式，经试验验证该公式具有较好的计算精度，具有较好的应用价值。

[1] 叶恩立，周宜红，肖焕雄，等. 钢筋石笼起动流速试验与流场结构数模分析[J]. 天津大学学报, 2014，47(2)：108-115.[2] 肖焕雄. 施工导截流与围堰工程研究[M]. 北京: 中国电力出版社, 2002.[3] 肖焕雄, 周克己. 对截流理论与实践中几个问题的初步讨论[J]. 水力发电学报, 1984，(2)：92-102.

[4] 李学海，程子兵，汪世鹏，等. 钢筋石笼的稳定性及其计算方法[J]. 长江科学院院报, 2013，30(8)：31-36.

[5] 黄国兵，李学海，程子兵，等. 截流块体稳定影响因素及实用计算公式[J]. 长江科学院院报, 2013,30(8)：25-30.[6] 李学海，唐祥甫，刘力中.明渠截流抛投体稳定性研究[J].三峡建设，2002，9(10)：26-27.

(编辑：陈 敏)

Influence of Void Ratio on the Stability Characteristics ofReinforced Gabion

GUO Hong-ming,ZHANG Tian-tian, HU Hai-song, HU Wen-bing

(School of Water Conservancy and Environmental Engineering,China Three Gorges University, Yichang 443002, China)

Reinforced gabion is a man-made material commonly used in closure, blocking and revetment projects. Exploring its stability mechanism is of vital significance to guiding its application. In this research, tests on the incipient motion of reinforced gabion of different shapes and void ratios were performed. Results suggest that given the same other influential factors, larger void ratio leads to better stability. The stability of reinforced gabions varies with different shapes. A formula of the incipient velocity of reinforced gabion in consideration of void ratio, size, density, shape, relative roughness and other factors was proposed to supplement and improve the classic formula, and is verified to be of good accuracy.

reinforced gabion; stability; conversion diameter; void ratio; incipient velocity; fitting of formula

2016-09-28；

2016-10-23

郭红民(1964-)，男，湖南湘西人，教授级高级工程师，硕士，主要从事水力学及河流动力学方向的研究，(电话)13972002877(电子信箱)4525073962@qq.com。

10.11988/ckyyb.20160999

2017,34(5):36-39,43

TV131

A

1001-5485(2017)05-0036-04