传统中值滤波算法与相关改进算法的特点
张佳晨

(浙江师范大学)
摘要:中值滤波算法由于算法简单方便被广泛应用在图像去噪中,但传统中值滤波算法处理图像过程中需要进行的排序次数较多导致图像处理速度较慢,在图像实时处理中不能很好的应用,因此许多学者对该算法中的排序算法进行改进,并提出了对中值滤波算法的改进算法。本文对传统中值滤波算法及几种快速中值滤波算法的特点进行了描述。
关键词:中值滤波算法;快速中值滤波算法;排序算法
0 引言
图像在成像、编码及传输等过程中,经常会受到各种干扰而形成噪声。这些噪声破坏了图像中一些像素点的原有灰度值,使得圖像不能真实地反映客观景象,图像质量下降,严重影响了后续的处理效果。因此,在对图像进行相关处理之前必须要进行滤波,以减小噪声的干扰。[1]中值滤波算法是一种常见的去噪算法,相对于其他线性平滑滤波的方法而言,中值滤波在处理随机噪声方面具有很强的降噪滤波能力。[2]而这种算法在处理质量、速度方面都存在着不足,国内外学者对其研究并优化,本文介绍了张国来、牛敏、马运强提出的三种改进后的快速中值滤波算法。
1传统中值滤波算法
1.1 传统中值滤波算法
中值滤波算法是对图像 中的每一个像素点的灰度值进行处理,基于统计学基础,对像素点灰度值进行排序达到去噪目的,具有非线性的特点。其具体过程如下(以二维中值滤波为例):取一像素点作为中心像素点,并以它为中心确定一个固定大小的滤波窗口,即确定它的邻域范围。
(x,y)为该中心像素点的位置,S_xy为以(x,y)为中心的邻域,(m,n)即为邻域中的任意一点,f(m,n)为点(m,n)的灰度值,Med{}即是对灰度值进行大小排序,并取中间值,f(x,y)为(x,y)灰度值,在上面这个公式中它的值经过该算法后将变为邻域中各个点灰度值的中值。以3*3的窗口大小为例,f(x,y)的值就是f(x-1,y),f(x-1,y-1),f(x-1,y+1),f(x,y),f(x,y-1),f(x,y+1),f(x+1,y),f(x+1,y-1),f(x+1,y+1)这几个点灰度值的中值,例如{6,1,2,4,5,0,3,2,3}即取3作为f(x,y)的值。
1.2优点
中值滤波算法方式简单,根据脉冲噪声的特点,这种噪声像素就会在排序时排在两边,使这种噪声像素得以消除。与均值滤波算法相比,不直接将窗口内的像素灰度值简单的平均,使图像的部分边缘、细节得以保留。
1.3缺点
从图像去噪处理速度的角度来看,传统中值滤波算法在排序过程中采用冒泡排序,且每次在滤波窗口移动后,都要进行重新排序。假设滤波窗口中共有n个像素点,每排序一次就需要进行n(n-1)/2次比较,其时间复杂度为O(n2),时间复杂度过于复杂。
从图像去噪处理效果的角度来看,根据其特点,对于高密度的噪声去噪效果比较差,很容易将信号点误判为噪声点。
2 快速中值滤波算法
快速中值滤波算法即对传统滤波算法中排序算法进行优化,提高其排序效率以此来提高对图像的处理速度。其中张国来提出了一种快速并行中值滤波算法[3],牛敏等学者提出了一种基于排序统计理论的快速中值滤波法[4],马运强等学者在牛敏等学者的基础上提出了快速中值滤波算法[5]。
2.1三种快速滤波算法的相同点
以3*3的滤波窗口为例,传统滤波算法通过冒泡排序求得中值,需要通过36次比较。这几种算法都通过先将这个滤波窗口的每行或者每列进行一个有序排列,在有序排列的基础上通过每个点可能大于或小于其它点数的个数来确定不可能为中值的点,从而减少之后要进行比较的点,使最终比较次数减少,提高算法效率。
2.2三种快速滤波算法的特点
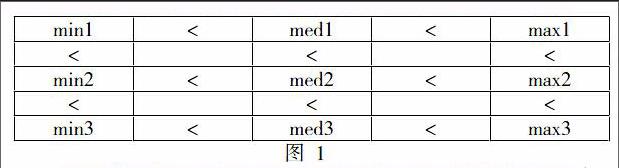
张国来提出的算法中将每列进行有序排列后,将这3列的最小值、中间值、最大值分别分在min、med、max这三组中,假设第一列三个点按大小顺序为min1、med1、max1,第二列三个点按大小顺序为min2、med2、max2,第三列同理,三列中最小、中间、最大值三组中的数与它们下标大小相同,如图1中所示,可以判断min1一定为最小值,min2至少小于min3、med3、max3,med2、max2,max3一定为最大值,max2至少大于max1、med1、min1、med2、min2,med1至少小于med2、med3、max1、max2、max3,med3一定大于min3、min2、min1、med2、med1,因此中值只可能在min3、max1、med2中产生,仅需要比较出这三个数的中值就可以确定中值。因此3列进行排序要进行9次比较,min中取出最小值需要进行2次比较,max中取最大值需要进行2次比较,而在med中取出中间值需要3次比较,最后三个数中取出中间值需要进行3次比较,因此总的比较次数为19次。
牛敏等学者提出来的算法将每行进行从小到大依次排序,之后与张国来不同之处在与将排序所得的三行的中值在按照从小到大依次排序,排序如图2所示按照箭头从小到大进行排序。由于将三行的中值也进行依次排序,几个数之间的相互关系有了更大的联系,与张国来在三组数中再次求出需要比较的点的思考方式不同,牛敏通过有序性这一特点进行比较。首先从图3中明显可以看到1、2点至少小于3、5、8、6、9,而8、9至少大于7、2、5、1、4,因此只需要在3、4、5、6、7这几个点中得出中值,由于此时4、5、6已经为有序排列,因此只需要将3、7与5比较,若3、7一个大于5,一个小于5,显然5为中值,若3、7同时小于5,那么中值将是4、3、7中的最大值,同时大于的情况也是同理。因此三行排列需要9次,中值的排列需要3次,3、7与5的比较需要2次,则最好情况为14次,若要进行最大值或者最小值的比较也需要2次,则最坏情况为16次,较之前张国来所提出的算法次数又一次进行了优化。
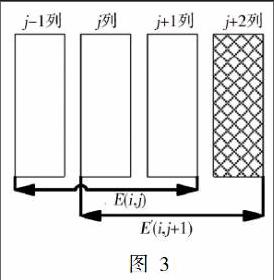
马云强等学者所提出的算法中对于滤波窗口中像素点排序的比较方法与牛敏一文中所提出的算法基本相同。而在这一基础上,马云强通过相邻窗口的相关性对相邻窗口间的中值比较进行了优化。以3*3的窗口为例,假设当前滤波窗口为E(xy),则将其水平平移向右移动一个像素点后,窗口变为E(x2y+1),而窗口中像素点只是最左列消除多增加了最右列,原来窗口中的两行不变,如图4所示。已知j、j+1列已经经过排序,因此只需要在对j+2列进行排序,而j、j+1列的中值已经按从小到大的顺序排列,因此对于j、j+1、j+2三行中的中值按从小到大排序只需要比较2次即可,之后按牛敏一文中的方法,通过有序性进行比较,最好情况一共需要7次,而最坏情况需要9次,若要对某一行中n个像素点进行中值处理时,在原来的算法要需要16n-14n之间,而改进后只需要9n-7n(n趋向于无穷大时),这大大提高了算法的效率。
参考文献:
[1]沈德海, 侯建, 鄂旭,等. 一种改进的加权均值滤波算法[J]. 现代电子技术, 2015(10):1-3.
[2]王松林, 蒋峥. 改进的自适应加权中值滤波算法[J]. 传感器与微系统, 2016, 35(11):128-131.
[3]张国来. 快速并行中值滤波的探讨[J]. 电子世界, 2014(18):407-408.
[4]牛敏, 邬战军, 牛燕雄,等. 一种基于排序统计理论的快速图像中值滤波法[J]. 电子测量技术, 2015(6):60-63.
[5]马运强, 魏利胜, 张平改,等. 一种快速的中值滤波算法[J]. 安徽工程大学学报, 2016, 31(4):63-67.

